1. Introduction
Simultaneous localization and mapping (SLAM) is an essential functionality required on a moving object for many applications where the localization or the motion estimation of this object must be determined from sensory data acquired by embedded sensors. The object is typically a robot or a vehicle, the position of which is required to deal with robust navigation in a cluttered environment. A SLAM module could also be required on smart tools (phones, glasses) to offer new services, e.g., augmented reality [
1,
2,
3].
The robot or smart tool could be equipped with a global navigation satellite system (GNSS) receiver for outdoor applications to obtain directly a position with respect to the Earth reference frame [
4]; at present, indoor localization with respect to a building reference frame could also be provided using ultra-wide band (UWB) [
5], WiFi [
6] or RF devices [
7], on the condition that a hotspot or antenna network has been previously installed and calibrated. However, the direct localization is not always available (
i.e., occlusions, bad propagation, multiple paths); so generally, they are combined using loose or tie fusion strategies, with motion estimates provided by an inertial measurement unit (IMU), integrating successive accelerometer and gyro data [
8,
9,
10]. Nevertheless, even GPS-IMU fusion could fail or be too inaccurate. Depending on the context,
a priori knowledge could be exploited; a map matching function can be sufficient, as in the GPS-based navigation systems available on commercial vehicles.
Considering mobile robots or the emerging autonomous vehicles, it is necessary to also make use of data acquired on the environment with embedded exteroceptive sensors, e.g., laser range finders [
11], 3D sensors (ToF cameras [
12], Kinect [
13]) or vision with many possible modalities (mono, stereo, omni). Here, only visual SLAM is considered, due to the fact that it could be integrated both in low-cost unmanned ground and aerial vehicles and on smart tools equipped with cameras. Many visual SLAM methods have been proposed during the last decade [
3,
14].
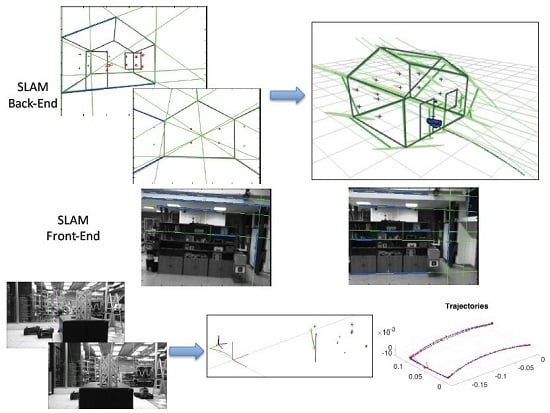
A SLAM method combines two interleaved functionalities shown in
Figure 1: the front-end detects and tracks features from images acquired from the moving robot, while the back-end, interpreting these feature and landmark observations, estimates both the landmark and robot positions with respect to the selected reference frame.
The back-end can be based either on estimation (Kalman [
15], information [
16], particle filters [
17]) or optimization (bundle adjustment) frameworks [
18]. The more classic landmarks are 3D points, detected as interest points (SIFT [
19], SURF [
20], FAST [
21]), matched by using their descriptors (binary robust independent elementary features (BRIEF) [
22]), or tracked by using Kanade-Lucas-Tomasi (KLT) feature tracker [
23], or an active-search strategy [
24]. Generally, the set of 3D points extracted from an image does not give any semantic information, unlike 3D lines, which correspond generally to sharp 3D edges in the environment. This is the reason why segment-based SLAM from either an estimation [
25] or optimization [
26] back-end, has been proposed. The main challenge of these methods concerns the front-end,
i.e., the robustness of the line detection and tracking in successive images.
The initialization of such landmarks with their minimal Euclidean parameters requires more than one observation. One way to solve this problem was the delayed initialization [
3,
27], in which a landmark was added to the map only when it was known in the Euclidean space. This does not allow use of landmarks that are very far from the robot. An alternative solution is to add them to the map, as soon as they are observed (
i.e., undelayed initialization), and it has been proposed for point [
28,
29] or line [
25] landmarks. The pros and cons of several representations for 3D points and 3D lines have been analyzed in [
30].
This article is devoted to the analysis of a visual SLAM solution using a heterogeneous map, as a more complete approach where points and lines are both included from features extracted in images acquired by a camera moving in the environment, and with undelayed initialization. Therefore, the contributions of the proposed method comprehend the use of heterogeneous landmark-based SLAM (the management of a map composed of heterogeneous landmarks), and from this perspective, the comparison between landmark parametrizations, the development of a front-end active-search process for linear landmarks integrated into SLAM (the processing of linear landmarks by the inclusion of detection and tracking algorithms taken from the state of the art) and the experimentation methodology. These contributions correspond to the gray blocks in
Figure 1. Only the first two contributions were covered in [
31], which dealt with the information fusion back-end for the map computation. The present article extends this concept to its application on real images, by developing the proposed front-end. Even if optimization-based methods make it possible to avoid the possible divergence of methods based on estimation due to linearization of the observation model, the fusion is performed from an extended Kalman filter, as a very light approach that can be integrated into a dedicated architecture to be used on small aerial vehicles.
Section 2 covers the techniques and parametrizations for the initialization and update of point and line landmarks on the map.
Section 3 describes the detection and tracking methods selected and developed for the front-end.
Section 4 focuses on experiments, including a simulation part that compares landmark representations, a real image part that recalls the integration of segments with the already existing point-based front-end and an integral experiment. The results of the experiments are presented and discussed in
Section 5. Finally,
Section 6 offers some conclusions.
2. SLAM Back-End
The SLAM back-end deals with the initialization of observed features as landmarks on the map and the estimation or update of both the landmarks and the robot positions with respect to a selected reference frame. This section deepens the description of each landmark parametrization, the initialization and update algorithms and it derives from the theoretical study presented in [
31].
The undelayed landmark initialization (ULI) is presented in [
30] for different point and line parametrizations. The main idea is to model the uncertainty derived from unmeasured degrees of freedom by a Gaussian prior that handles unbounded limits, in a manner that can be handled by EKF.
The implications of uncertainty are different for point and line landmarks. For points, depth is initially unknown, and uncertainty is present along the visual ray until infinity. In the case of infinite straight lines, uncertainty is present in two degrees of freedom, corresponding to a depth that should be covered up to infinity and all possible orientations.
2.1. 3D Point Parametrizations
In this section, a Euclidean point is described as a reference, for subsequent covering of the ones used for initialization purposes (i.e., homogeneous point and anchored homogeneous point). Each description includes camera projection and back-projection.
Point parametrizations used for initialization are shown in
Figure 2.
2.1.1. Euclidean Point
A Euclidean point is parametrized by its Cartesian coordinates.
The projection to the camera frame is performed as follows:
where,
is the intrinsic parameter matrix and
and
are the rotation matrix and translation vector that define the camera
. Homogeneous coordinates are represented by underlined vectors, like
.
2.1.2. Homogeneous Point
Homogeneous points are four-vector composed of the 3D vector
m and scalar
ρ, as introduced in [
32].
The vector m gives the direction from the origin to the point p, while ρ serves as a scale factor for providing the magnitude for each coordinate of the point.
The conversion from homogeneous to Euclidean coordinates is given by the following equation:
Depending on the characteristics of the parameters m and ρ, there are three different canonical representations for a homogeneous point. The original Euclidean point refers to the case when ρ = 1, inverse-depth has and in inverse-distance .
In the camera frame,
m is the director vector of the optical ray, and
ρ has a linear dependence on the inverse of the distance
d defined from the optical center to the point:
The unbounded distance of a point along the optical ray from zero to infinity can then be expressed in the bounded interval in parameter space .
The frame transformation of a homogeneous point is performed according to the next equation:
where super-index
indicates the frame to which the point is referred and matrix
H specifies the frame to which the point is transformed.
The projection of a homogeneous point into the image frame is performed with the following equation:
By expressing a homogeneous point in the camera frame, the projected image point is
, where super-index
indicates the frame to which the point is referred. In this case,
is not measurable. Back-projection is then:
The complete homogeneous point parametrization is the following:
where
must be given as a prior and represents the inverse-distance from the origin of the coordinates, that is the scalar value that makes
.
2.1.3. Anchored Homogeneous Point
Linearity is supposed to be improved by the addition of an anchor that serves as a reference to the optical center at the initialization time of the landmark. The landmark is then composed of seven elements that include Cartesian coordinates of the anchor, the point with respect to the anchor and an inverse-distance scalar.
The conversion from the anchored homogeneous point to Euclidean coordinates can be obtained by the following equation:
The projection and frame transformation process is given below:
The anchor is chosen to be the position of the optical center at the initialization time, given by
. That way, the term multiplying the unmeasured degree of freedom
ρ (
i.e.,
) is small after initialization. This helps to decouple the uncertainty of the most uncertain parameter
ρ. The complete anchored homogeneous point parametrization for back projection and transformation is the following:
where
must be given as the prior.
2.2. 3D Line Parametrizations
The line parametrization includes the projection to the image frame and back-projection to 3D.
The Plücker line and anchored homogeneous point line are shown in
Figure 3.
2.2.1. Plücker Line
Plücker coordinates are conformed by a six-vector that represents a line in
defined by two points
and
:
where
,
,
, with the Plücker constraint:
.
In terms of geometry,
n is the vector normal to the plane
π containing the line and the origin and
v is the director vector from
to
. The Euclidean orthogonal distance from the line to the origin is given by
. Hence,
is the inverse-distance, analogous to
ρ of homogeneous points. Plücker line geometrical representation is shown in
Figure 3a.
Expressions for transformation and inverse-transformation of Plücker coordinates from and to the camera frame are as shown next:
The transformation and projection process in terms of
,
,
n and
v is as follows:
where the intrinsic projection Plücker matrix
is defined as:
When Plücker coordinates are expressed in the camera frame, projection is obtained by:
The range and orientation of the line are included in and are not measurable.
For Plücker line back projection, vectors
and
are obtained with these expressions:
where
and
are mutually orthogonal.
Defining
, vector
can also be expressed as:
where
for any value of
β. Plücker line back projection is shown in
Figure 3b.
The complete Plücker line parametrization for back projection and transformation is given in the following equation:
where
β must be provided as a prior.
2.2.2. Anchored Homogeneous Points Line
A line can also be represented by the end points defining it. With the application of the anchored homogeneous point parametrization, shown in
Figure 3c, an anchored homogeneous-points line is an eleven-vector defined as follows:
For each point, the transformation and projection of a pinhole camera is as previously stated in Equation (4).
A homogeneous 2D line is obtained by the cross product of two points lying on it,
, giving:
In comparison to the result obtained for Plücker coordinates, the product is a vector orthogonal to the plane π, analogous to the Plücker sub-vector n. Furthermore, the term is a vector that gives the direction between the points of the line, therefore related to Plücker sub-vector v.
The complete anchored homogeneous point line parametrization for back projection and transformation is the following:
where
and
must be given as priors.
2.3. Landmark Initialization
The process of the initialization of a landmark consists of the detection of a feature in the image, retro-projection to 3D and inclusion into the map. There are three important concepts that are involved in the landmark initialization: the 3D landmark
x itself, the 2D measurement
z of the landmark in the image and the unmeasured degree of freedom
π. All of these are modeled as Gaussian variables, whose notation is
. Thus, the cited concepts are expressed as
,
and
, respectively. The 3D landmarks
x considered for this study are points and lines, already described in
Section 2.1 and
Section 2.2. The parametrizations for landmark 2D measurements
z and unmeasured degrees of freedom
π, as well as the description of the initialization algorithm are covered in the following sections.
2.3.1. Landmark 2D Measurements in the Image
Points are represented as a two-vector containing Cartesian coordinates in pixel space, leading to the following:
where
U is the covariance matrix of the position of the point.
In homogeneous coordinates,
Lines can be expressed by a four-vector that represents the coordinates of their end-points, also with a Gaussian probability density function.
The probability density function for infinite lines like Plücker,
, is composed of the homogeneous line representation and the covariance matrix defined as follows:
2.3.2. Unmeasured Degrees of Freedom
The uncertainty in 3D points and lines coming from projection is represented by inverse-distance variables and , which are modeled as Gaussian variables. The origin of each of these priors must be inside the of their probability density functions.
For points and end-point-based lines, the minimum distance must match the upper
boundary, hence:
The probability density function of a point based line is defined as
, with:
The Plücker lines prior
take the following values:
This initializes lines at the front of the camera.
2.3.3. Undelayed Landmark Initialization Algorithm
The ULI algorithm was presented in [
30] for the construction of landmark-based stochastic maps, including a single type of landmark
. The approach presented in this paper includes heterogeneous parametrizations of landmarks
on the same map, where
can be a point or line. The resulting algorithm is composed of the following steps:
Identify mapped magnitudes .
Identify measurements , where is either a point or a line (i.e., or , respectively).
Define Gaussian prior for the unmeasured degree of freedom. π can either be , or .
Back-project the Gaussian measurement, and get the landmark mean and Jacobians.
where
is the back projection and transformation function for the corresponding landmark.
is the camera frame expressed in terms of its position
and orientation
in quaternion nomenclature.
Compute landmarks’ co- and cross-variances.
2.4. Landmark Update
The purpose of the landmark update process is to recalculate the parameters of the elements on the map, (
i.e., the robot and landmark poses), given the observation of the already mapped landmarks in the current frame. This process starts by projecting all of the observable landmarks to the image plane and selecting those with higher uncertainty for correction. For points, the observation function
h() applies a homogeneous to Euclidean transformation
h2e() once having performed the projection process previously explained, as follows:
Innovation mean
y and covariance
Y is then obtained as shown next:
where
is the measurement noise covariance and Jacobian
.
For lines, the innovation function computes the orthogonal distances from the detected end-points
to a line
l, as shown in
Figure 4, leading to the following:
Since the EKF innovation is the difference between the actual measurement and the expectation and
z is the orthogonal distance previously described, the line innovation function is:
as the desired orthogonal distance from the predicted line to the matched end-points is zero.
A landmark is found consistent if the squared Mahalanobis distance
MD2 of innovation is smaller than a threshold
MD2
th.
As that is true, the landmark is updated:
Point and line parametrizations are modeled as Gaussian variables in [
25,
29,
30], validating the use of Mahalanobis distance as compared to a chi-squared distribution. Kalman gain is assumed to be optimal. Since this process is intended to be developed as a light approach that could be integrated into a dedicated architecture on small vehicles, the selected covariance update formula is used instead of the Joseph form, which has such a high complexity that it may compromise performance. Successful results of this formulation are presented in [
30].
4. Experiments
This section includes the experimental part that tests the three main contributions of this article. The first part deals with the back-end and consists of a comparative evaluation between different landmark parametrizations. A set of simulations tests the benefits of the combination of point and line landmarks in the same map. The following part deals with the implementation of the developed segment-based SLAM front-end that includes the line segment active-search process presented in this paper. Finally, a complete heterogeneous landmark-based SLAM experiment that integrates the contributions to back-end and front-end is included.
4.1. Simulation of the Back-End for Heterogeneous SLAM
The point and line parametrizations previously presented have been tested independently in previous studies, such as [
25,
29,
30]. This section offers a comparison of different heterogeneous approaches, including combinations of distinct landmarks on the same map. The purpose is to show the benefits of working with a heterogeneous parametrization that combines points and lines in a single map. The combinations performed are enumerated below:
The MATLAB® EKF-SLAM toolbox [
44] was extended with the heterogeneous functionality to perform the simulations.
Figure 10a shows the simulation environment. It consists of a house conformed by 23 lines and an array of 16 points distributed uniformly among the walls.
The robot performs two different trajectories. The first one is a circular path of 5 m in diameter, with a pose step of 8 cm and 0.09°. The second is a motion of 70 steps of 4 cm, each taken towards the scene. The linear noise is 0.5 cm and the angular noise 0.05°.
Besides the heterogeneous landmark capability of the toolbox, the transparency of the objects in the scene was also considered. By default, objects in the simulation environment of the toolbox are transparent, so landmarks are visible on almost every image frame. To work in a more realistic manner, an aspect graph was implemented to only observe visible surfaces of the house at each camera pose.
Both transparent and opaque object visualizations are shown in
Figure 11. An example of a heterogeneous map constructed after a complete turn of the robot around the house is shown in
Figure 10b. The parametrization used is AHP + PL. For the case of the approaching trajectory, a final heterogeneous map constructed is shown in
Figure 10c. The parametrization used is AHP + AHPL. They display in green the line landmarks estimated and in blue the point landmarks. Real, predicted and estimated robot trajectories are displayed in blue, red and green, respectively.
For the circular path, a trajectory of five turns, considering transparent and opaque objects, was performed for each parametrization.
4.2. Integration of Line Segment Active-Search to the SLAM Front-End
The line-based SLAM front-end that was developed and that implements the line segment active-search presented in this article is covered in this section. The LSD and ME algorithms were applied to an image sequence showing a piece of furniture inside a room.
Figure 12 shows the operation of this segment-based front-end of an EKF-SLAM process. Infinite thin lines represent the estimated position of the landmark in the current image, while thicker segments show the match found. It can be observed that the match corresponds to the estimation in most of the cases.
4.3. Heterogeneous SLAM Experiment
The complete heterogeneous SLAM solution was tested with the experiment described in this section.
The mobile robot used was a CRS Robotics F3 system, with a Microsoft LifeCam Studio camera mounted on it, along with a 9DOF Razor IMU that provided the robot state estimation at each frame. A total of 401 images with a 1280 × 720 resolution form the sequence. From this robot, it was possible to get the ground truth information with a repeatability of ±0.05 mm. The robot described a total trajectory of 0.4653 m. To get a prediction of the motion, the information provided by the IMU was used in a constant acceleration motion model. The inclusion of this additional sensor made it possible to cope with the inherent scale ambiguity of monocular systems.
Figure 13 presents certain frames of the sequence, showing the landmarks used to update the state of the map. The AHP and AHPL were the parametrizations selected for the experiments, as they were the ones that provided better simulation results.
5. Results and Discussion
For the analysis, root mean square error (RMSE) evaluation is used to compute errors. At each instant
k, the estimated position
is compared to the ground truth position
.
From the previous results, the mean and standard deviation of the error are computed as follows:
Simulation of the back-end for heterogeneous SLAM was intended to compare the different parametrizations and to show the benefits of landmark heterogeneity.
The parametrization with the highest error is the Plücker line. Anchored parametrizations achieved the best performance, for both points and lines. There is an improvement effect in line parametrizations by the addition of points. Even for the anchored cases, already having a relative good performance while working independently, the heterogeneity improves the results, in such a way that the combination of both AHP and AHPL is the one with the least error along the simulated trajectories.
The position error of the robot in the case of a circular trajectory with transparent and opaque objects is shown in
Figure 14; these results are summarized in
Table 1. For the case of the approaching trajectory, the results are shown and summarized in
Figure 15 and
Table 2.
The complete SLAM experiment integrating the back-end with the developed front-end is used to compare the heterogeneous approach with a classic point-based SLAM applied to the same sequence. The ground truth and estimated trajectories for each SLAM approach tested are shown in
Figure 16.
Figure 17 presents results in terms of the robot position estimation error, comparing the IMU estimation to both point and heterogeneous SLAM. As can be observed, the heterogeneous approach results in lower errors, as previously presented in the simulation part. Near Frame 200, there was a change in the motion direction of the robot, which can be seen as a peak in the position estimation error graph. Even in this case, heterogeneous SLAM achieved a better performance than the point-based SLAM.
Table 3 shows a comparative summary of the errors from the three cases.
6. Conclusions
The purpose of this paper is to prove the benefits of including heterogeneous landmarks when building a map from an EKF-based visual SLAM method. Several authors have shown interest in the use of heterogeneous landmarks. For the front-end, the interest for joint tracking of points and lines is found in [
45], while for the back-end, a theoretical study is presented in [
31], and preliminary results of an EKF-based SLAM method, based on heterogeneous landmarks, are presented in [
46]. The experiments performed that the authors describe have shown that the robot localization or the SLAM stability can be improved by combining several landmarks,
i.e., points and lines. The use of just monocular vision provides only partial observations of landmarks by features extracted from images; here, undelayed initialization of landmarks is used, as was proposed initially by Solà
et al. [
25,
29] for points and lines. The use of simulated data has shown how the choice of the landmark representation has an impact on the accuracy of the map. The best ones, considering the construction of a map with heterogeneous landmarks, are anchored homogeneous points and anchored homogeneous points lines. These parametrizations were used in a complete heterogeneous SLAM experiment that produced better results than the classic point-based case, by reducing the camera position estimation error.
Another contribution of this paper is a method proposed for a segment-based SLAM front-end. This method relies on the line segment active-search process presented in this article and on state-of-the-art line detection and matching processes. The methods that compose the developed front-end that resulted were discussed, recalling, first, their theoretical background and, then, presenting some experimental evaluations on image sequences that show the stability of the process.
Finally, a complete heterogeneous landmark-based SLAM experiment was presented, integrating the contributions with the back-end and the front-end and confirming the results obtained independently.
In future work, constraints will be exploited in the map, typically when points and lines are extracted from known portions of the scene.