A Plasmonic Temperature-Sensing Structure Based on Dual Laterally Side-Coupled Hexagonal Cavities
Abstract
:1. Introduction
2. The Sensing Structure and Theoretical Analysis
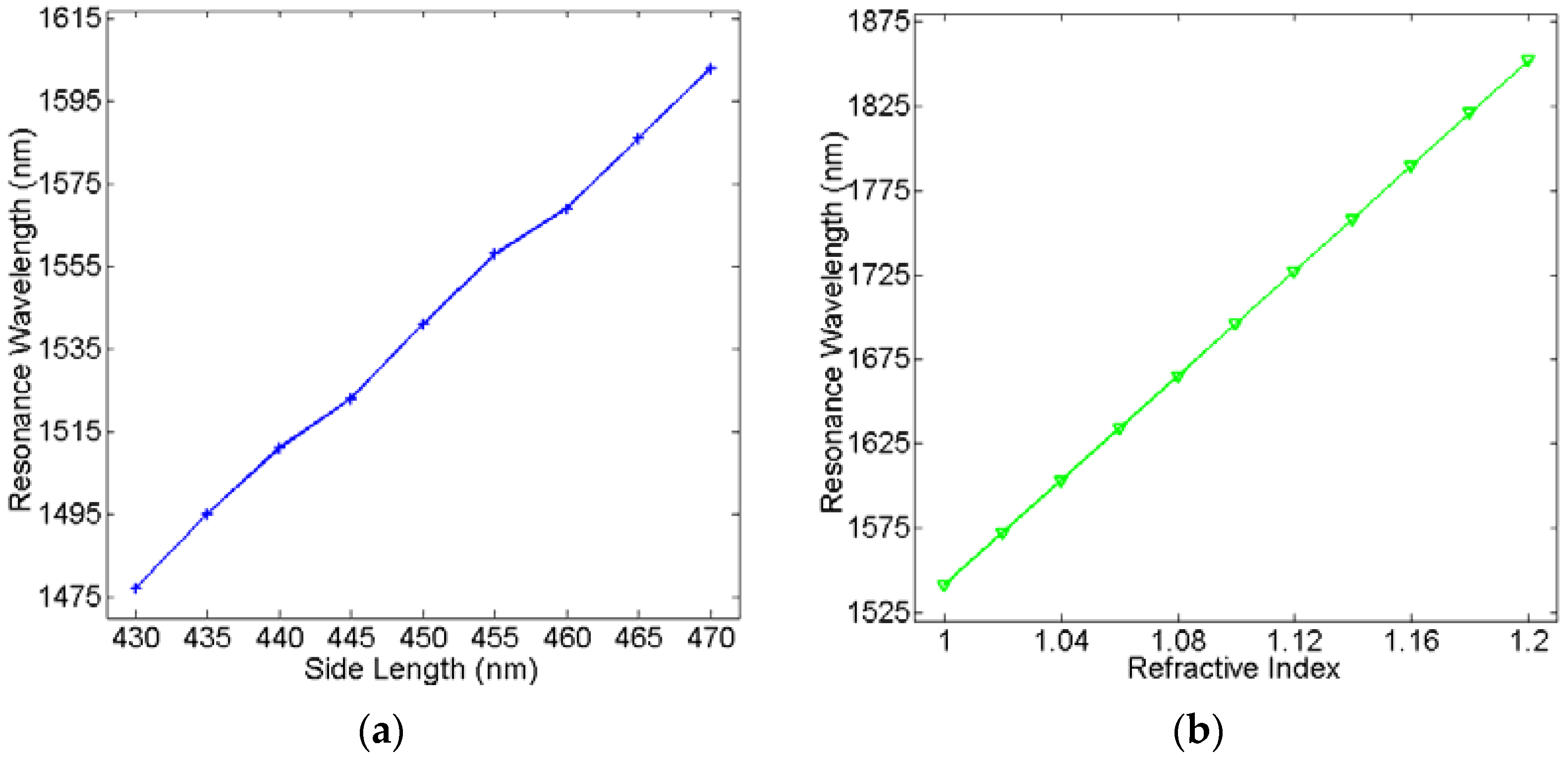
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Andersen, T.B.; Han, Z.H.; Bozhevolnyi, S.I. Compact on-chip temperature sensors based on dielectric-loaded plasmonic waveguide-ring resonators. Sensors 2011, 11, 1992–2000. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.G.; Han, M.; Hou, W.L. High-resolution and fast-response fiber-optic temperature sensor using silicon Fabry-Pérot cavity. Opt. Express 2015, 23, 7237–7247. [Google Scholar] [CrossRef] [PubMed]
- Zhan, Y.; Xue, S.; Yang, Q.; Xiang, S.; He, H.; Zhu, R. A novel fiber Bragg grating high-temperature sensor. Opt Int. J. Light Electron. Opt. 2008, 119, 535–539. [Google Scholar] [CrossRef]
- Kou, J.L.; Ding, M.; Feng, J.; Lu, Y.Q.; Xu, F.; Brambilla, G. Microfiber-based Bragg gratings for sensing applications: A review. Sensors 2012, 12, 8861–8876. [Google Scholar] [CrossRef] [PubMed]
- Shao, L.Y.; Luo, Y.; Zhang, Z.; Zou, X.; Luo, B.; Pan, W.; Yan, L. Sensitivity-enhanced temperature sensor with cascaded fiber optic Sagnac interferometers based on Vernier-effect. Opt. Commun. 2014, 336, 73–76. [Google Scholar] [CrossRef]
- Geng, Y.; Li, X.; Tan, X.; Deng, Y.; Hong, X. Compact and ultrasensitive temperature sensor with a fully liquid-filled photonic crystal fiber Mach-Zehnder interferometer. IEEE Sens. J. 2014, 14, 167–170. [Google Scholar] [CrossRef]
- Rong, Q.; Sun, H.; Qiao, X.; Zhang, J.; Hu, M.; Feng, Z. Corrigendum: A miniature fiber-optic temperature sensor based on a Fabry-Perot interferometer. J. Opt. 2012, 14. [Google Scholar] [CrossRef]
- Wu, D.; Zhu, T.; Liu, M. A high temperature sensor based on a peanut-shape structure Michelson interferometer. Opt. Commun. 2012, 285, 5085–5088. [Google Scholar] [CrossRef]
- Srivastava, S.K.; Gupta, B.D. Simulation of a localized surface-plasmon-resonance-based fiber optic temperature sensor. J. Opt. Soc. Am. A 2010, 27, 1743–1749. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Hou, J.; Huang, Z.; Lu, Q. Temperature sensor based on surface plasmon resonance within selectively coated photonic crystal fiber. Appl. Opt. 2012, 51, 6361–6367. [Google Scholar] [CrossRef] [PubMed]
- Fukano, H.; Kushida, Y.; Taue, S. Sensitivity improvement of optical-fiber temperature sensor with solid cladding material based on multimode interference. Jpn. J. Appl. Phys. 2015, 54. [Google Scholar] [CrossRef]
- Silva, S.; Pachon, E.G.; Franco, M.A.; Hayashi, J.G.; Malcata, F.X.; Frazão, O.; Cordeiro, C. Ultrahigh-sensitivity temperature fiber sensor based on multimode interference. Appl. Opt. 2012, 51, 3236–3242. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Hafezi, M.; Fan, J.; Taylor, J.M.; Strouse, G.F.; Ahmed, Z. Ultra-sensitive chip-based photonic temperature sensor using ring resonator structures. Opt. Express 2014, 22, 3098–3104. [Google Scholar] [CrossRef] [PubMed]
- Kim, G.D.; Lee, H.S.; Park, C.H.; Lee, S.S.; Lim, B.T.; Bae, H.K.; Lee, W.G. Silicon photonic temperature sensor employing a ring resonator manufactured using a standard CMOS process. Opt. Express 2010, 18, 22215–22221. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, T.; Ritwick, D.; Rajan, J. Highly sensitive plasmonic temperature sensor based on photonic crystal surface plasmon waveguide. Plasmonics 2012, 8, 515–521. [Google Scholar] [CrossRef]
- Shen, X.; Cui, T.J. Ultrathin plasmonic metamaterial for spoof localized surface plasmons. Laser Photonics Rev. 2014, 8, 137–145. [Google Scholar] [CrossRef]
- Huidobro, P.A.; Shen, X.; Cuerda, J.; Moreno, E.; Martin-Moreno, L.; Garcia-Vidal, F.J.; Pendry, J.B. Magnetic localized surface plasmons. Phys. Rev. X 2014, 4. [Google Scholar] [CrossRef]
- Liao, Z.; Luo, Y.; Fernández-Domínguez, A.I.; Shen, X.; Maier, S.A.; Cui, T.J. High-order localized spoof surface plasmon resonances and experimental verifications. Sci. Rep. 2015, 5, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Liao, Z.; Shen, X.; Pan, B.C.; Zhao, J.; Luo, Y.; Cui, T.J. Combined system for efficient excitation and capture of LSP resonances and flexible control of SPP transmissions. ACS Photon. 2015, 2, 738–743. [Google Scholar] [CrossRef]
- Ditlbacher, H.; Krenn, J.R.; Schider, G.; Leitner, A.; Aussenegg, F.R. Two-dimensional optics with surface plasmon polaritons. Appl. Phys. Lett. 2002, 81, 1762–1764. [Google Scholar] [CrossRef]
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef] [PubMed]
- Maier, S.A.; Atwater, H.A. Plasmonics: Localization and guiding of electromagnetic energy in metal/dielectric structures. J. Appl. Phys. 2005, 98. [Google Scholar] [CrossRef]
- Barnes, W.L. Surface plasmon-polariton length scales: A route to sub-wavelength optics. J. Opt. A Pure Appl. Opt. 2006, 8, S87–S93. [Google Scholar] [CrossRef]
- Ebbesen, T.W.; Genet, C.; Bozhevolnyi, S.I. Surface-plasmon circuitry. Phys. Today 2008, 61, 44–50. [Google Scholar] [CrossRef]
- Gramotnev, D.K.; Bozhevolnyi, S.I. Plasmonics beyond the diffraction limit. Nat. Photon. 2010, 4, 83–91. [Google Scholar] [CrossRef]
- Zhai, X.; Wang, L.; Wang, L.L.; Li, X.F.; Huang, W.Q.; Wen, S.C.; Fan, D.Y. Tuning bandgap of a double-tooth-shaped MIM waveguide filter by control widths of the teeth. J. Opt. 2013, 15. [Google Scholar] [CrossRef]
- Lu, H.; Liu, X.; Mao, D.; Wang, L.; Gong, Y. Tunable band-pass plasmonic waveguide filters with nanodisk resonators. Opt. Express 2010, 18, 17922–17927. [Google Scholar] [CrossRef] [PubMed]
- Lu, F.; Wang, Z.; Li, K.; Xu, A. A plasmonic triple-wavelength demultiplexing structure based on MIM waveguide with side-coupled nanodisk cavities. IEEE Trans. Nanotechnol. 2013, 12, 1185–1189. [Google Scholar] [CrossRef]
- Chen, Z.; Hu, R.; Cui, L.; Yu, L.; Wang, L.; Xiao, J. Plasmonic wavelength demultiplexers based on tunable Fano resonance in coupled-resonator systems. Opt. Commun. 2014, 320, 6–11. [Google Scholar] [CrossRef]
- Guo, Y.; Yan, L.; Pan, W.; Luo, B.; Wen, K.; Guo, Z.; Luo, X. A plasmonic splitter based on slot cavity. Opt. Express 2011, 19, 13831–13838. [Google Scholar] [CrossRef] [PubMed]
- Wen, K.; Hu, Y.; Chen, L.; Zhou, J.; Lei, L.; Guo, Z. Design of an optical power and wavelength splitter based on subwavelength waveguides. J. Lightw. Technol. 2014, 32, 3020–3026. [Google Scholar] [CrossRef]
- Lu, H.; Liu, X.M.; Wang, L.R.; Gong, Y.K.; Mao, D. Ultrafast all-optical switching in nanoplasmonic waveguide with Kerr nonlinear resonator. Opt. Express 2011, 19, 2910–2915. [Google Scholar] [CrossRef] [PubMed]
- Tao, J.; Wang, Q.; Huang, X. All-optical plasmonic switches based on coupled nano-disk cavity structures containing nonlinear material. Plasmonics 2011, 6, 753–759. [Google Scholar] [CrossRef]
- Dolatabady, A.; Granpayeh, N. All optical logic gates based on two dimensional plasmonic waveguides with nanodisk resonators. J. Opt. Soc. Korea 2012, 16, 432–442. [Google Scholar] [CrossRef]
- Bian, Y.; Gong, Q. Compact all-optical interferometric logic gates based on one-dimensional metal-insulator-metal structures. Opt. Commun. 2013, 313, 27–35. [Google Scholar] [CrossRef]
- Jin, X.; Huang, X.; Tao, J.; Lin, X.; Zhang, Q. A novel nanometeric plasmonic refractive index sensor. IEEE Trans. Nanotechnol. 2010, 9, 134–137. [Google Scholar]
- Zhu, J.; Huang, X.; Tao, J.; Jin, X.; Mei, X. Nanometeric plasmonic refractive index senor. Opt. Commun. 2012, 285, 3242–3245. [Google Scholar] [CrossRef]
- Dolatabady, A.; Granpayeh, N.; Nezhad, V.F. A nanoscale refractive index sensor in two dimensional plasmonic waveguide with nanodisk resonator. Opt. Commun. 2013, 300, 265–268. [Google Scholar] [CrossRef]
- Yun, B.; Hu, G.; Zhang, R.; Cui, Y. Design of a compact and high sensitive refractive index sensor based on MIM plasmonic bragg grating. Opt. Express 2014, 22, 28662–28670. [Google Scholar]
- Zou, S.; Wang, F.; Liang, R.; Xiao, L.; Hu, M. A nanoscale refractive index sensor based on asymmetric plasmonic waveguide with a ring resonator. IEEE Sens. J. 2013, 15, 646–650. [Google Scholar] [CrossRef]
- Wu, T.; Liu, Y.; Yu, Z.; Peng, Y.; Shu, C.; He, H. The sensing characteristics of plasmonic waveguide with a single defect. Opt. Commun. 2014, 323, 44–48. [Google Scholar] [CrossRef]
- Wu, T.; Liu, Y.; Yu, Y.Z.; Peng, Y.; Shu, C.; Ye, H. The sensing characteristics of plasmonic waveguide with a ring resonator. Opt. Express 2014, 22, 7669–7677. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Liu, Y.; Yu, Z.; Ye, H.; Peng, Y.; Shu, C.; He, H. A nanometeric temperature sensor based on plasmonic waveguide with an ethanol-sealed rectangular cavity. Opt. Commun. 2014, 339, 1–6. [Google Scholar] [CrossRef]
- Wang, T.; Wen, X.; Yin, C.; Wang, H. The transmission characteristics of surface plasmon polaritons in ring resonator. Opt. Express 2009, 17, 24096–24101. [Google Scholar] [CrossRef] [PubMed]
- Rakic, A.D.; Djurišic, A.B.; Elazar, J.M.; Majewski, M.L. Optical properties of metallic films for vertical-cavity optoelectronic devices. Appl. Opt. 1998, 37, 5271–5283. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Huang, Y.; Zhao, W.; Xu, W.; He, C. A novel plasmonic sensor based on metal-insulator-metal waveguide with side-coupled hexagonal cavity. IEEE Photon. J. 2015, 7. [Google Scholar] [CrossRef]
- Xu, L.; Wang, S.; Wu, L. Refractive index sensing based on plasmonic waveguide side-coupled with bilaterally-located double cavities. IEEE Trans. Nanotechnol. 2014, 13, 875–879. [Google Scholar] [CrossRef]
- Yee, K.S. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
- Dongjun Tech. East FDTD, 3rd ed.; Dongjun Information Technology Co.: Shanghai, China, 2012; pp. 10–14.










© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Huang, Y.; Xu, W.; Zhao, W.; He, C. A Plasmonic Temperature-Sensing Structure Based on Dual Laterally Side-Coupled Hexagonal Cavities. Sensors 2016, 16, 706. https://doi.org/10.3390/s16050706
Xie Y, Huang Y, Xu W, Zhao W, He C. A Plasmonic Temperature-Sensing Structure Based on Dual Laterally Side-Coupled Hexagonal Cavities. Sensors. 2016; 16(5):706. https://doi.org/10.3390/s16050706
Chicago/Turabian StyleXie, Yiyuan, Yexiong Huang, Weihua Xu, Weilun Zhao, and Chao He. 2016. "A Plasmonic Temperature-Sensing Structure Based on Dual Laterally Side-Coupled Hexagonal Cavities" Sensors 16, no. 5: 706. https://doi.org/10.3390/s16050706
APA StyleXie, Y., Huang, Y., Xu, W., Zhao, W., & He, C. (2016). A Plasmonic Temperature-Sensing Structure Based on Dual Laterally Side-Coupled Hexagonal Cavities. Sensors, 16(5), 706. https://doi.org/10.3390/s16050706





