Diaphragm Based Fiber Bragg Grating Acceleration Sensor with Temperature Compensation
Abstract
:1. Introduction
2. Working Principle and Modeling of the Proposed Sensor
2.1. Temperature Sensing Model
2.2. Vibration Sensing Model
3. Numerical Analysis for Structure Design
4. Experiments and Discussion
4.1. Characterization of Temperature Effect
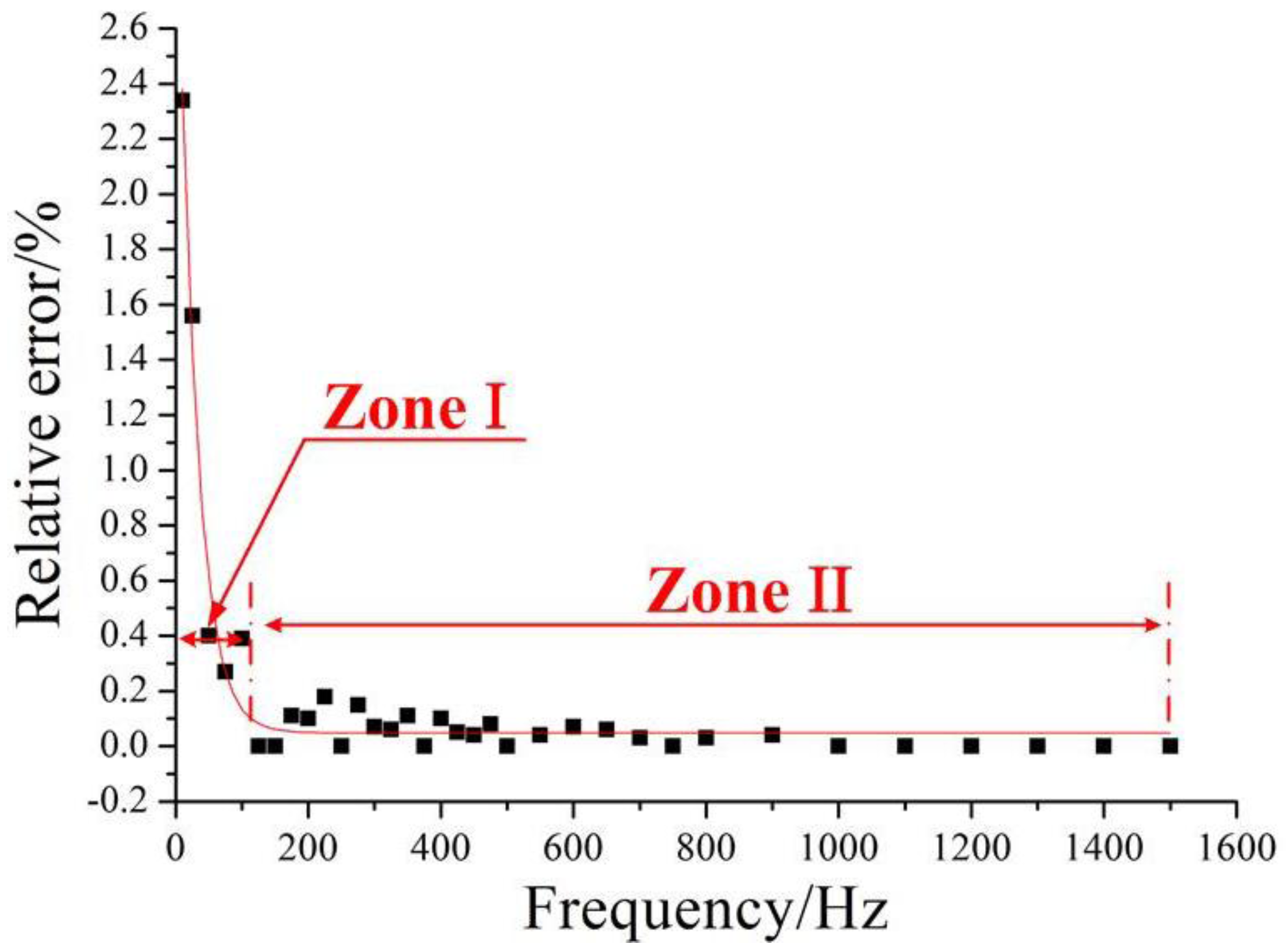
4.2. Characterization of Static Properties
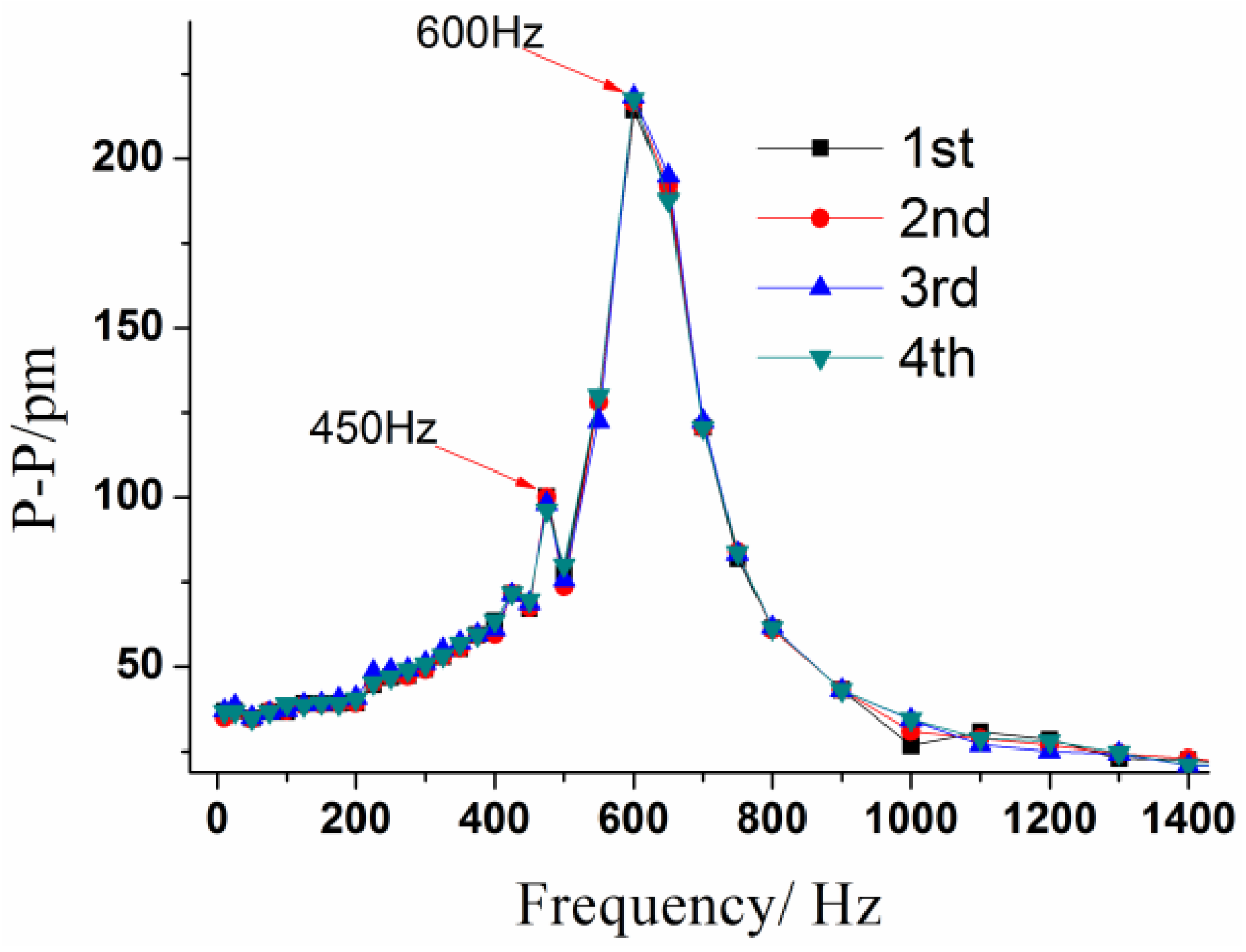
4.3. Characterization of Dynamic Properties
4.4. Characterization of Cross-Sensitivity
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lee, B. Review of the present status of optical fiber sensors. Opt. Fiber Technol. 2003, 9, 57–79. [Google Scholar] [CrossRef]
- Hill, K.O.; Meltz, G. Fiber Bragg grating technology fundamentals and overview. J. Lightwave Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef]
- Majumder, M.; Gangopadhyay, T.K.; Chakraborty, A.K.; Dasgupta, K.; Bhattacharya, D.K. Fibre Bragg gratings in structural health monitoring—Present status and applications. Sens. Actuators A Phys. 2008, 147, 150–164. [Google Scholar] [CrossRef]
- Chen, J.J.; Liu, B.; Zhang, H. Review of fiber Bragg grating sensor technology. Front. Optoelectron. China 2011, 4, 204–212. [Google Scholar] [CrossRef]
- Hong, C.Y.; Zhang, Y.F.; Zhang, M.X.; Leung, L.M.G.; Liu, L.Q. Application of FBG sensors for geotechnical health monitoring, a review of sensor design, implementation methods and packaging techniques. Sens. Actuators A Phys. 2016, 244, 184–197. [Google Scholar] [CrossRef]
- Guo, Y.X.; Zhang, D.S.; Zhou, Z.D.; Zhu, F.D.; Xiong, L. Development and commissioning of FBG sensors for impact test of rock fall protective barrier. Sens. Rev. 2014, 34, 343–348. [Google Scholar] [CrossRef]
- Cai, L.; Tan, Y.G.; Wei, Q. Nonlinear vibration-FBG sensing technique for plate detection. Sens. Rev. 2015, 35, 287–295. [Google Scholar] [CrossRef]
- Wu, J.; Masek, V.; Cada, M. The possible use of fiber Bragg grating based accelerometers for seismic measurements. In Proceedings of the 2nd Canadian Conference on Electrical and Computer Engineering (CCECE’09), St John’s, NL, Canada, 3–6 May 2009; pp. 860–863.
- Au, H.Y.; Khijwania, S.K.; Tam, H.Y. Fiber Bragg grating based accelerometer. In Proceedings of the 19th International Conference on Optical Fiber Sensors, Perth, WA, Australia, 14–18 April 2008.
- Basumallick, N.; Biswas, P.; Dasgupta, K.; Bandyopadhyay, S. Design optimization of fiber Bragg grating accelerometer for maximum sensitivity. Sens. Actuators A Phys. 2013, 194, 31–39. [Google Scholar] [CrossRef]
- Khan, M.M.; Panwar, N.; Dhawan, R. Modified cantilever beam shaped FBG based accelerometer with self temperature compensation. Sens. Actuators A Phys. 2014, 205, 79–85. [Google Scholar] [CrossRef]
- Liu, Q.P.; Qiao, X.G.; Zhao, J.L.; Jia, Z.A.; Gao, H.; Shao, M. Novel fiber Bragg grating accelerometer based on diaphragm. IEEE Sens. J. 2012, 12, 3000–3004. [Google Scholar] [CrossRef]
- Da Costa Antunes, P.F.; Lima, H.F.T.; Alberto, N.J.; Rodrigues, H.; Pinto, P.M.F.; de Lemos Pinto, J.; Nogueira, R.N.; Varum, H.; Costa, A.G.; de Brito Andre, P.S. Optical fiber accelerometer system for structural dynamic monitoring. IEEE Sens. J. 2009, 9, 1347–1354. [Google Scholar] [CrossRef]
- Antunes, P.; Varum, H.; André, P. Uniaxial fiber Bragg grating accelerometer system with temperature and cross axis insensitivity. Measurement 2011, 44, 55–59. [Google Scholar] [CrossRef]
- Weng, Y.Y.; Qiao, X.G.; Guo, T.; Hu, M.; Feng, Z.; Wang, R.; Zhang, J. A robust and compact fiber Bragg grating vibration sensor for seismic measurement. IEEE Sens. J. 2011, 12, 800–804. [Google Scholar] [CrossRef]
- Li, T.L.; Tan, Y.G.; Zhou, Z.D. A Fiber Bragg Grating Sensing-Based Micro-Vibration Sensor and Its Application. Sensors 2016, 16, 547. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.T.; Yen, C.T.; Wu, Y.S.; Cheng, H.C. Using a Fiber Loop and Fiber Bragg Grating as a Fiber Optic Sensor to Simultaneously Measure Temperature and Displacement. Sensors 2013, 13, 6542–6551. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.R.; Lv, Q. Sensor Technical Manual; Beihang University Press: Beijing, China, 2007; Volume 7. [Google Scholar]
- Li, T.L.; Tan, Y.G.; Wei, L.; Zheng, K.; Guo, Y.X. A non-contact fiber Bragg grating vibration sensor. Rev. Sci. Instrum. 2014, 85. [Google Scholar] [CrossRef] [PubMed]
- Shao, R.P. Mchanical System Dynamics; Mechanical Industry Press: Beijing, China, 2005. [Google Scholar]











| Type | Linearity % | Hysteresis Error/% | Fitted Equation |
|---|---|---|---|
| #1FBG | 2.36 | 8.76 | ∆λ1 = 0.00997 × T + 1297.63452 (∆λ10:nm) |
| #2FBG | 1.30 | 2.04 | ∆λ2 = 0.00866 × T + 1307.62474 (∆λ2:nm) |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Tan, Y.; Han, X.; Zheng, K.; Zhou, Z. Diaphragm Based Fiber Bragg Grating Acceleration Sensor with Temperature Compensation. Sensors 2017, 17, 218. https://doi.org/10.3390/s17010218
Li T, Tan Y, Han X, Zheng K, Zhou Z. Diaphragm Based Fiber Bragg Grating Acceleration Sensor with Temperature Compensation. Sensors. 2017; 17(1):218. https://doi.org/10.3390/s17010218
Chicago/Turabian StyleLi, Tianliang, Yuegang Tan, Xue Han, Kai Zheng, and Zude Zhou. 2017. "Diaphragm Based Fiber Bragg Grating Acceleration Sensor with Temperature Compensation" Sensors 17, no. 1: 218. https://doi.org/10.3390/s17010218
APA StyleLi, T., Tan, Y., Han, X., Zheng, K., & Zhou, Z. (2017). Diaphragm Based Fiber Bragg Grating Acceleration Sensor with Temperature Compensation. Sensors, 17(1), 218. https://doi.org/10.3390/s17010218







