Implementation of High Time Delay Accuracy of Ultrasonic Phased Array Based on Interpolation CIC Filter
Abstract
:1. Introduction
2. Interpolation CIC Filter Parallel Algorithm
2.1. CIC Filter with Traditional Structure
2.2. Interpolation CIC Filter Parallel Algorithm
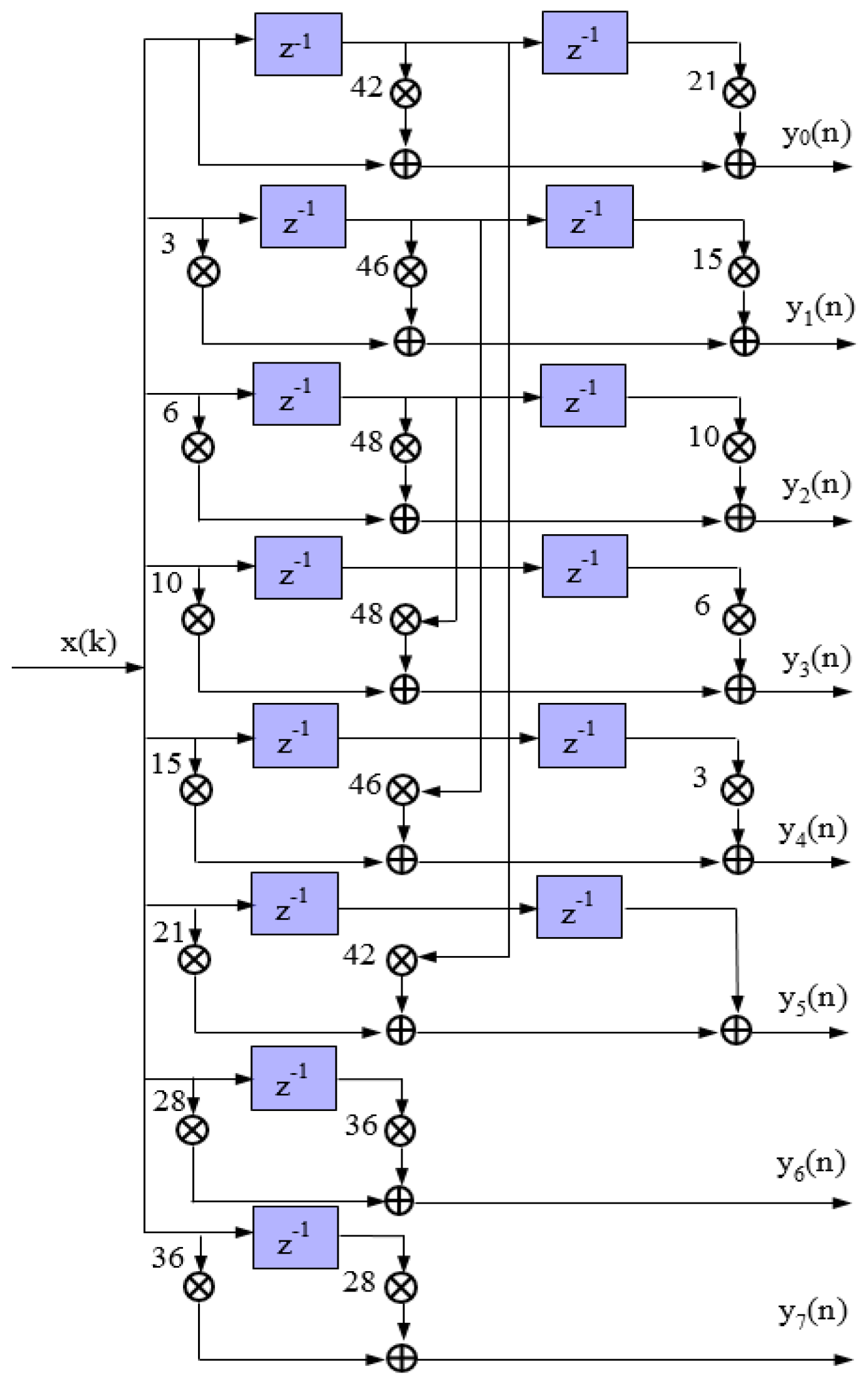
2.3. Structure Optimization of 8× Interpolation CIC Filter Parallel Algorithm
2.4. The Principle of Ultrasonic Phased Array Focusing Time Delay Based on 8× Interpolation CIC Filter Parallel Algorithm
3. Compensation of CIC Filter
3.1. Performance Analysis of CIC Filter
3.2. Compensated CIC Filter
4. Simulation and Experiments
4.1. Simulation of 8× Interpolation CIC Filter Parallel Algorithm
4.2. Experiments of Defect Echo Detection
4.3. Experiments of Time Delay Accuracy
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xu, D.S.; Zhao, Y.M. Deformation monitoring of metro tunnel with a new ultrasonic-based system. Sensors 2017, 17, 1758. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Gong, S.F. Ultrasonic phased array detection of internal defects in composite insulators. IEEE Trans. Dielect. Electr. Insul. 2016, 23, 525–531. [Google Scholar]
- Shi, K.R.; Guo, Y.M. Phased Array Ultrasonic Imaging and Testing; Higher Education Press: Beijing, China, 2010; pp. 1–10. [Google Scholar]
- Quaegebeur, N.; Masson, P. Correlation-based imaging technique using ultrasonic transmit-receive array for non-destructive evaluation. Ultrasonics 2012, 52, 1056–1064. [Google Scholar] [CrossRef] [PubMed]
- Ko, R.T.; Chen, M.Y. Ultrasonic measurements of velocity for modulus assessment of a material using a delay line approach. AIP Conf. Proc. 2013, 1511, 1446–1453. [Google Scholar]
- Song, T.K.; Greenleaf, J.F. Ultrasonic dynamic focusing using an analog FIFO and asynchronous sampling. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1994, 41, 326–332. [Google Scholar] [CrossRef]
- Cassereau, D.; Fink, M. Time-reversal of ultrasonic fields. III. Theory of the closed time-reversal cavity. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1992, 39, 579–592. [Google Scholar] [CrossRef] [PubMed]
- Lie, I.; Tanase, M.E. About the possibility to implement a nonuniform oversampling receive beamformer in a FPGA. IEEE Ultrason. Symp. 2005, 2, 1404–1407. [Google Scholar]
- Liang, J.; Wang, Z.; Shi, Y.W. Ultrasonic inspection of thick parts with phased array dynamic focusing. In Proceedings of the 10th European Conference on Non-Destructive Testing, Moscow, Russia, 7 June 2010; pp. 986–992. [Google Scholar]
- Wang, J.L.; Wang, X.D. The focus steering for high intensity focused ultrasound phased array based on real-time phase shifts calculating. Acta Acust. 2010, 35, 303–308. [Google Scholar]
- Cruza, J.F.; Camacho, J. New method for real-time dynamic focusing through interfaces. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 739–751. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.X.; Tang, W.M. Focusing time delay of ultrasonic phased array based on multistage half-band filter. Opti. Precis. Eng. 2014, 22, 1571–1576. [Google Scholar]
- Khyam, M.O.; Ge, S.S. Highly accurate time-of-flight measurement technique based on phased-correlation for ultrasonic ranging. IEEE Sens. J. 2017, 17, 434–443. [Google Scholar] [CrossRef]
- Liu, J.; Jin, S.J.; Chen, S.L. Design of an ultrasonic phase-controlled transmitter with high integration. Chin. J. Sens. Actuators 2010, 23, 1106–1110. [Google Scholar]
- Hogenauer, E. An economical class of digital filters for decimation and interpolation. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 155–162. [Google Scholar] [CrossRef]
- Lyons, R. Understanding cascaded integrator-comb filters. Embed. Syst. Program. 2005, 18, 14–27. [Google Scholar]
- Dolecek, G.J. Design of wideband CIC compensator filter for a digital IF receiver. Digit. Signal Process. 2009, 19, 827–837. [Google Scholar] [CrossRef]
- Dolecek, G.J.; Mitra, S.K. On design of CIC decimation filter with improved response. In Proceedings of the IEEE International Symposium on Communications, Control, and Signal Processing, St Julians, Malta, 12–14 March 2008; pp. 1072–1076. [Google Scholar]
- Du, Y. Inplementation of Digital Filter on MATLAB and FPGA: Altera/Verilog; Publishing House of Electronics Industry: Beijing, China, 2015; pp. 185–193. [Google Scholar]
- Jang, Y.; Yang, S. Non-recursive cascaded integrator-comb decimation filters with integrator-comb decimation filters with integer multiple factors. In Proceedings of the 44th IEEE Midwest Symposium on Circuits and Systems, Dayton, OH, USA, 14–17 August 2001; Volume 1, pp. 130–133. [Google Scholar]
- Stephen, G.; Stewart, R.W. High-speed sharpening of decimating CIC filter. Electron. Lett. 2004, 40, 1383–1384. [Google Scholar] [CrossRef]
- Romero, D.E.T.; Salgado, G.M. Simple two-adders CIC compensator. Electron. Lett. 2015, 51, 993–994. [Google Scholar] [CrossRef]
- Devi, K.; Mehra, R. Improved maximally flat wideband CIC compensation filter using sharpening technique. Int. Comput. Appl. 2015, 116, 6–9. [Google Scholar] [CrossRef]
- Khan, I.R. Flat magnitude response FIR halfband low/high pass digital filters with narrow transition bands. Digit. Signal Process. 2010, 20, 328–336. [Google Scholar] [CrossRef]















| 4× | 5× | 6× | 7× | 8× | 9× | 10× | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 12 | 3 | 1 | 18 | 6 | 1 | 25 | 10 | 1 | 33 | 15 | 1 | 42 | 21 | 1 | 52 | 28 | 1 | 63 | 36 |
| 3 | 12 | 1 | 3 | 19 | 3 | 3 | 27 | 6 | 3 | 36 | 10 | 3 | 46 | 15 | 3 | 57 | 21 | 3 | 69 | 28 |
| 6 | 10 | 0 | 6 | 18 | 1 | 6 | 27 | 3 | 6 | 37 | 6 | 6 | 48 | 10 | 6 | 60 | 15 | 6 | 73 | 21 |
| 10 | 6 | 0 | 10 | 15 | 0 | 10 | 25 | 1 | 10 | 36 | 3 | 10 | 48 | 6 | 10 | 61 | 10 | 10 | 75 | 15 |
| 15 | 10 | 0 | 15 | 21 | 0 | 15 | 33 | 1 | 15 | 46 | 3 | 15 | 60 | 6 | 15 | 75 | 10 | |||
| 21 | 15 | 0 | 21 | 28 | 0 | 21 | 42 | 1 | 21 | 57 | 3 | 21 | 73 | 6 | ||||||
| 28 | 21 | 0 | 28 | 36 | 0 | 28 | 52 | 1 | 28 | 69 | 3 | |||||||||
| 36 | 28 | 0 | 36 | 45 | 0 | 36 | 63 | 1 | ||||||||||||
| 45 | 36 | 0 | 45 | 55 | 0 | |||||||||||||||
| 55 | 45 | 0 | ||||||||||||||||||
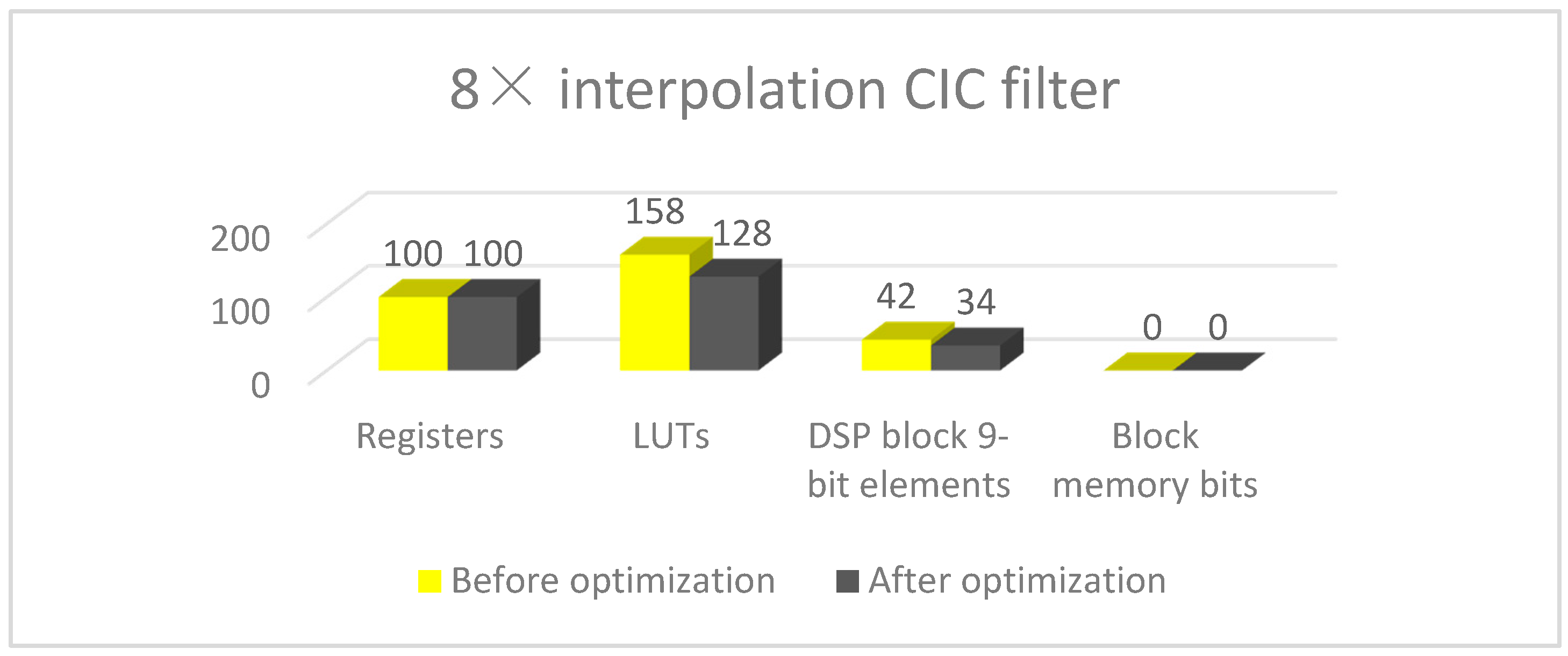
| Algorithm | 8× Interpolation CIC Filter | 8× Interpolation Half-Band Filter |
|---|---|---|
| Multiplications | 17k | 30k |
| Additions | 14k | 27k |
| LUTs | 128 | 272 |
| Registers | 100 | 94 |
| DSP block 9-bit | 34 | 52 |
| Memory bits | 0 | 20 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Li, X.; Li, H.; Su, Z.; Zhang, H. Implementation of High Time Delay Accuracy of Ultrasonic Phased Array Based on Interpolation CIC Filter. Sensors 2017, 17, 2322. https://doi.org/10.3390/s17102322
Liu P, Li X, Li H, Su Z, Zhang H. Implementation of High Time Delay Accuracy of Ultrasonic Phased Array Based on Interpolation CIC Filter. Sensors. 2017; 17(10):2322. https://doi.org/10.3390/s17102322
Chicago/Turabian StyleLiu, Peilu, Xinghua Li, Haopeng Li, Zhikun Su, and Hongxu Zhang. 2017. "Implementation of High Time Delay Accuracy of Ultrasonic Phased Array Based on Interpolation CIC Filter" Sensors 17, no. 10: 2322. https://doi.org/10.3390/s17102322
APA StyleLiu, P., Li, X., Li, H., Su, Z., & Zhang, H. (2017). Implementation of High Time Delay Accuracy of Ultrasonic Phased Array Based on Interpolation CIC Filter. Sensors, 17(10), 2322. https://doi.org/10.3390/s17102322




