Design Optimisation of a Magnetic Field Based Soft Tactile Sensor
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sensor Concept
2.1.1. Sensor Mechanics
2.1.2. Magnetic Field
2.1.3. Structural Mechanics
2.2. Design Specification
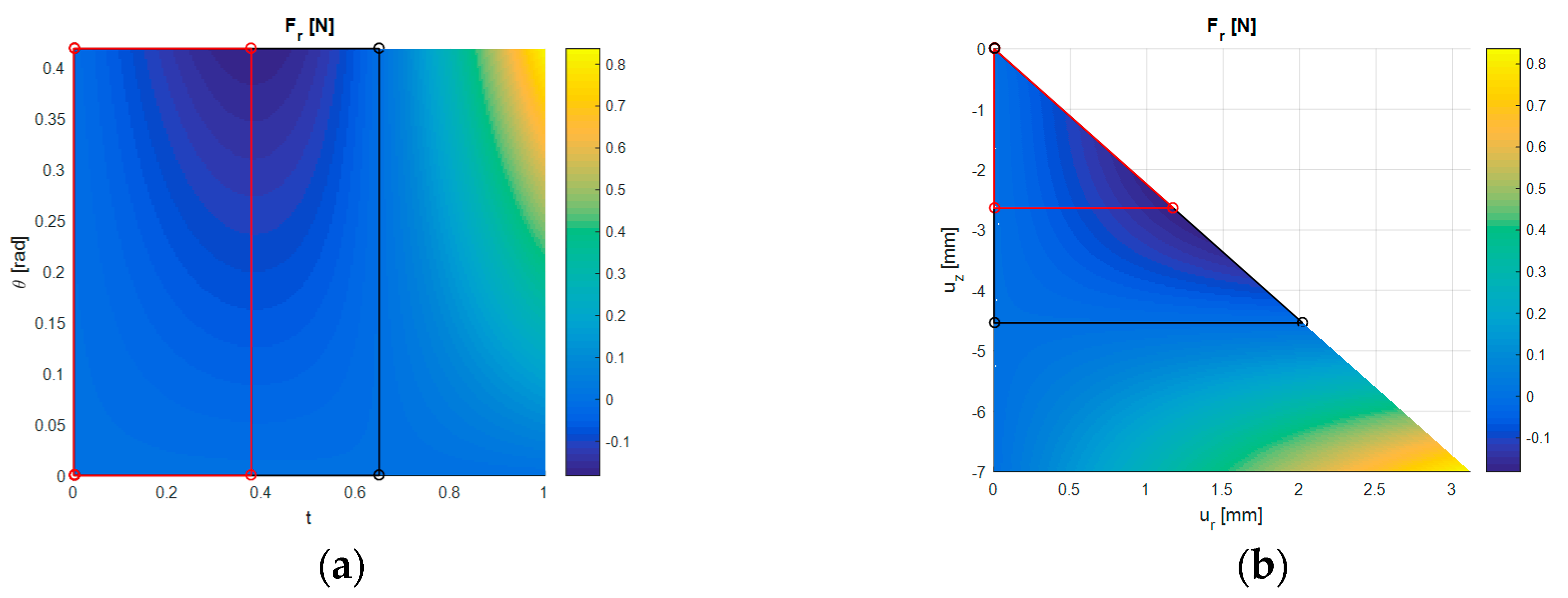
2.2.1. Parameterisation
2.2.2. Loading Stability
2.2.3. Design Optimisation
2.3. Numerical Simulations
2.3.1. Magnetic Field Simulation
2.3.2. Structural Mechanics Simulations
2.3.3. Genetic Programming
2.3.4. Optimisation Procedure
2.4. Design Validation
3. Results
3.1. Magnetic Field
3.2. Strcutural Mechanics
3.3. Sensitivity
3.4. Design Optimisation
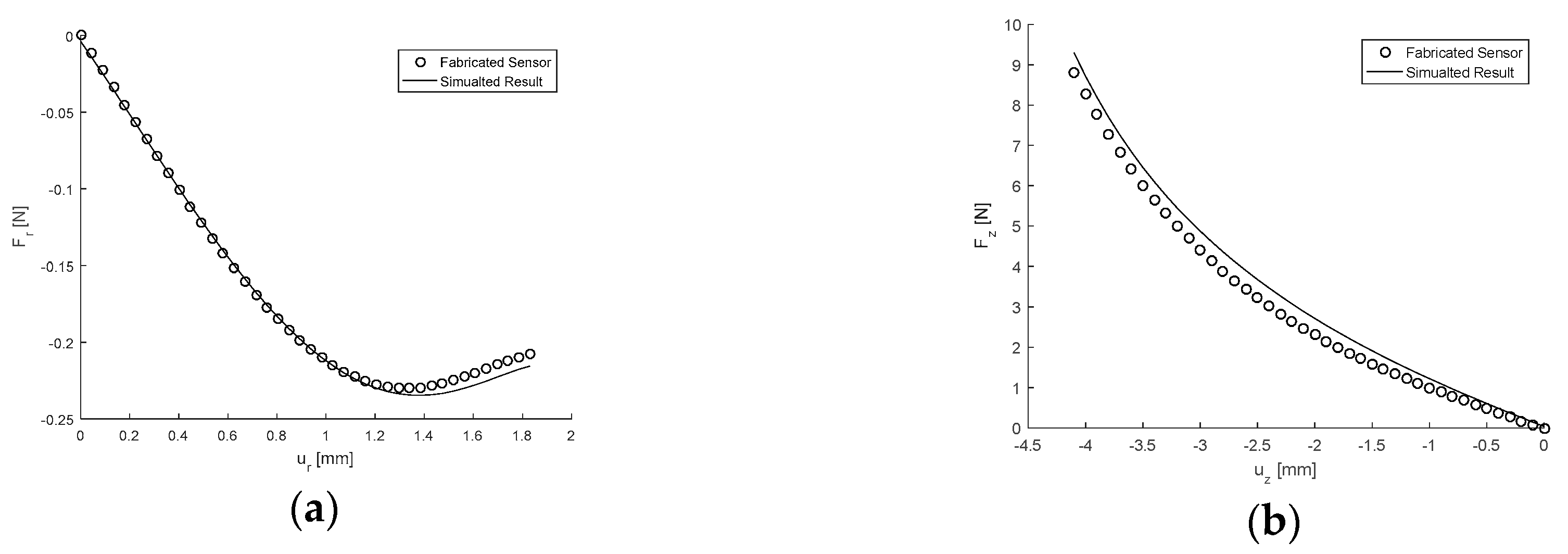
3.5. Design Validation
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A

References
- Bartolozzi, C.; Natale, L.; Nori, F.; Metta, G. Robots with a sense of touch. Nat. Mater. 2016, 15, 921–925. [Google Scholar] [CrossRef] [PubMed]
- Kappassov, Z.; Corrales, J.A.; Perdereau, V. Tactile sensing in dexterous robot hands—Review. Robot. Auton. Syst. 2015, 74, 195–220. [Google Scholar] [CrossRef]
- Dahiya, R.S.; Metta, G.; Valle, M.; Sandini, G. Tactile sensing—From humans to humanoids. IEEE Trans. Robot. 2010, 26, 1–20. [Google Scholar] [CrossRef]
- Lee, H.K.; Chung, J.; Chang, S.I.; Yoon, E. Real-time measurement of the three-axis contact force distribution using a flexible capacitive polymer tactile sensor. J. Micromech. Microeng. 2011, 21, 035010. [Google Scholar] [CrossRef]
- Winstone, B.; Griffiths, G.; Melhuish, C.; Pipe, T.; Rossiter, J. TACTIP–tactile fingertip device, challenges in reduction in size to ready for robot hand integration. In Proceedings of the 2012 IEEE International Conference on Robotics and Biomimetics, Guangzhou, China, 11–14 December 2012. [Google Scholar]
- Wettles, N.; Santos, V.J.; Johansson, R.S.; Loeb, G.E. Biomimetic tactile sensor array. Adv. Robot. 2008, 22, 829–849. [Google Scholar] [CrossRef]
- Clark, J.J. A magnetic field based compliance matching sensor for high resolution, high compliance tactile sensing. In Proceedings of the 1988 IEEE International Conference on Robotics and Automation, Philadelphia, PA, USA, 24–29 April 1988; pp. 772–777. [Google Scholar]
- Jamone, L.; Natale, L.; Metta, G.; Sandini, G. Highly sensitive soft tactile sensors for an anthropomorphic robotic hand. IEEE Sens. J. 2015, 15, 4226–4233. [Google Scholar] [CrossRef]
- Wang, H.; de Boer, G.N.; Kow, J.; Alazmani, A.; Ghajari, M.; Hewson, R.W.; Culmer, P.R. Design methodology for magnetic field based soft tri-axis tactile sensors. Sensors 2016, 16, 1356. [Google Scholar] [CrossRef] [PubMed]
- Tomo, T.P.; Somlor, S.; Schmitz, A.; Jamone, L.; Huang, W.; Kristanto, H.; Sugano, S. Design and characterization of a three-axis Hall effect based soft skin sensor. Sensors 2016, 16, 491. [Google Scholar] [CrossRef] [PubMed]
- De Oliveria, T.; Cretu, A.M.; Petriu, E.M. Multimodal bio-inspired tactile sensing module. IEEE Sens. J. 2017, 17, 3231–3243. [Google Scholar] [CrossRef]
- Wang, H.; de Boer, G.N.; Kow, J.; Alazmani, A.; Ghajari, M.; Hewson, R.W.; Culmer, P.R. A low-cost soft tactile sensing array using 3D Hall sensors. Procedia Eng. 2016, 168, 650–653. [Google Scholar] [CrossRef]
- Shin, J.; Spicer, J.P.; Abell, J.A. Inverse and direct magnetic shaping problems. Struct. Multidiscip. Optim. 2012, 46, 285–301. [Google Scholar] [CrossRef]
- Jia, F.; Liu, Z.; Zaitsev, M.; Henning, J.; Korvink, J.G. Design multiple-layer gradient coils using least-squares finite element method. Struct. Multidiscip. Optim. 2014, 49, 523–535. [Google Scholar] [CrossRef]
- Barthold, F.J.; Firuziaan, M. Optimization of hyperelastic materials with isotropic damage. Struct. Multidiscip. Optim. 2000, 20, 12–21. [Google Scholar] [CrossRef]
- Parsons, R.; Canfield, S.L. Developing genetic programming techniques for the design of compliant mechanisms. Struct. Multidiscip. Optim. 2002, 24, 78–86. [Google Scholar] [CrossRef]
- Lin, J.; Luo, Z.; Tong, L. A new multi-objective programming scheme for topology optimization of compliant mechanisms. Struct. Multidiscip. Optim. 2010, 40, 241–255. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, S. Development of soft sensor system via dynamic optimization. In Proceedings of the 30th Annual Conference of the IEEE Industrial Electronics Society, Busan, Korea, 2–6 November 2004. [Google Scholar]
- Xu, Z.; Kolev, S.; Todorov, E. Design, optimization, calibration, and a case study of a 3D-printed, low-cost fingertip sensor for robotic manipulation. In Proceedings of the 2014 IEEE Conference on Robotics & Automation, Hong Kong, China, 31 May–7 June 2014. [Google Scholar]
- Zheng, Q.Z.; Querin, O.M.; Barton, D.C. Geometry and sizing optimisation of discrete structure using the genetic programming method. Struct. Multidiscip. Optim. 2006, 31, 452–461. [Google Scholar] [CrossRef]
- Fawaz, Z.; Xu, Y.G.; Behdinan, K. Hybrid evolutionary algorithm and application to structural optimization. Struct. Multidiscip. Optim. 2005, 30, 219–226. [Google Scholar] [CrossRef]
- Maiolino, F.; Galantini, F.; Mastrogiovanni, G.; Gallone, G.; Cannata, G.; Capri, F. Soft dielectrics for capacitive sensing in robot skins: Performance of different elastomer types. Sens. Actuators A Phys. 2015, 226, 37–47. [Google Scholar] [CrossRef]
- Ribeiro, P.; Khan, M.A.; Alfadhel, A.; Kosel, J.; Franco, F.; Cardoso, S.; Bernardino, A.; Schmitz, A.; Santos-Victor, J.; Jamone, L. Bio-inspired ciliary force sensor for robotic platforms. IEEE Robot. Autom. Lett. 2017, 2, 971–976. [Google Scholar] [CrossRef]
- Nuelle, K.; Schultz, M.J.; Aden, S.; Dick, A.; Munske, B.; Gaa, J.; Kotlarski, J.; Ortmaier, T. Force sensing, low-cost manipulator in mobile robotics. In Proceedings of the 2017 IEEE Conference on Control, Automation and Robotics, Nagoya, Japan, 22–24 April 2017. [Google Scholar]
- Paulino, T.; Ribeiro, P.; Neto, M.; Cardoso, S.; Schmitz, A.; Santos-Victor, J.; Bernadino, A.; Jamone, L. Low-cost 3-axis soft tactile sensor for the human-friendly robot Vizzy. In Proceedings of the 2017 IEEE Conference on Control, Automation and Robotics, Nagoya, Japan, 22–24 April 2017. [Google Scholar]
- Wan, L.; Wang, B.; Wang, Q.; Han, J.; Cao, S. The output characteristic of cantilever-like tactile sensor based on the inverse magnetoresistive effect. AIP Adv. 2017, 7, 056805. [Google Scholar] [CrossRef]
- Chung, D.D.L. Electromagnetic interference shielding effectiveness of carbon materials. Carbon 2001, 39, 279–285. [Google Scholar] [CrossRef]
- Sparks, J.L.; Vavalle, N.A.; Kasting, K.E.; Long, B.; Tanaka, M.L.; Sanger, P.A.; Schnell, K.; Conner-Kerr, T.A. Use of silicone materials to simulate tissue biomechanics as related to deep tissue injury. Adv. Skin Wound Care 2015, 28, 59–68. [Google Scholar] [CrossRef] [PubMed]
- Koza, J. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, UK, 1992; Volume 1. [Google Scholar]
- De Boer, G.N.; Wang, H.; Ghajari, M.; Alazmani, A.; Hewson, R.W.; Culmer, P.R. Force and topography reconstruction using GP and MOR for the TACTIP soft sensor system. In Towards Autonomous Robotic Systems TAROS 2016; Alboul, L., Groß, R., Melhuish, C., Witkowski, M., Prescott, T.J., Penders, J., Eds.; Springer: Berlin, Germany, 2016; pp. 65–74, LNAI 9716. [Google Scholar]
- COMSOL Inc., USA. Comsol Multiphysics 5.3 [Computer Software]. 2017. Available online: https://www.comsol.com/ (accessed on 28 September 2017).
- Dassault Systèmes, France. Abaqus CAE 2017 [Computer Software]. 2016. Available online: https://www.3ds.com/ (accessed on 28 September 2017).
- Zhang, M.; Mak, A.F.T. In vivo frictional properties of human skin. Prosthet. Orthot. Int. 2009, 23, 135–141. [Google Scholar]
- Searson, D. GPTIPS [Computer Software]. 2016. Available online: http://sites.google.com/site/GPTIPS4matlab/ (accessed on 28 September 2017).
- The MathWorks Inc., USA. Matlab R2017a [Computer Software]. 2017. Available online: https://www.mathworks.com/ (accessed on 28 September 2017).
- Hazewinkel, M. Minimax Principle, Encyclopaedia of Mathematics; Springer: Berlin, Germany, 2001; ISBN 978-1-55608-010-4. [Google Scholar]
- Form2, USA. Clear Resin GPCL02. 2017. Available online: https://www.formlabs.com/ (accessed on 28 September 2017).
- Smooth-On Inc., USA. EcoFlex 00-30. 2017. Available online: https://www.smooth-on.com/products/ecoflex-00-30/ (accessed on 28 September 2017).
- Smooth-On Inc., USA. Sil-poxy. 2017. Available online: https://www.smooth-on.com/product-line/sil-poxy/ (accessed on 28 September 2017).
- ATI Industrial Automation, USA. Nano17-E. 2017. Available online: https://www.ati-ia.com/ (accessed on 28 September 2017).
- Zaber Technologies Inc., Canada. T-LSR75B. 2017. Available online: https://www.zaber.com/ (accessed on 28 September 2017).
- National Instruments, USA. LabView 2017 [Computer Software]. 2017. Available online: https://www.ni.com/ (accessed on 28 September 2017).
- Gupta, G. Dynamic Low, High and Band Pass Filter [Computer Software]. 2012. Available online: https://uk.mathworks.com/matlabcentral/fileexchange/31985-dynamic-low--high-and-band-pass-filter/ (accessed on 28 September 2017).








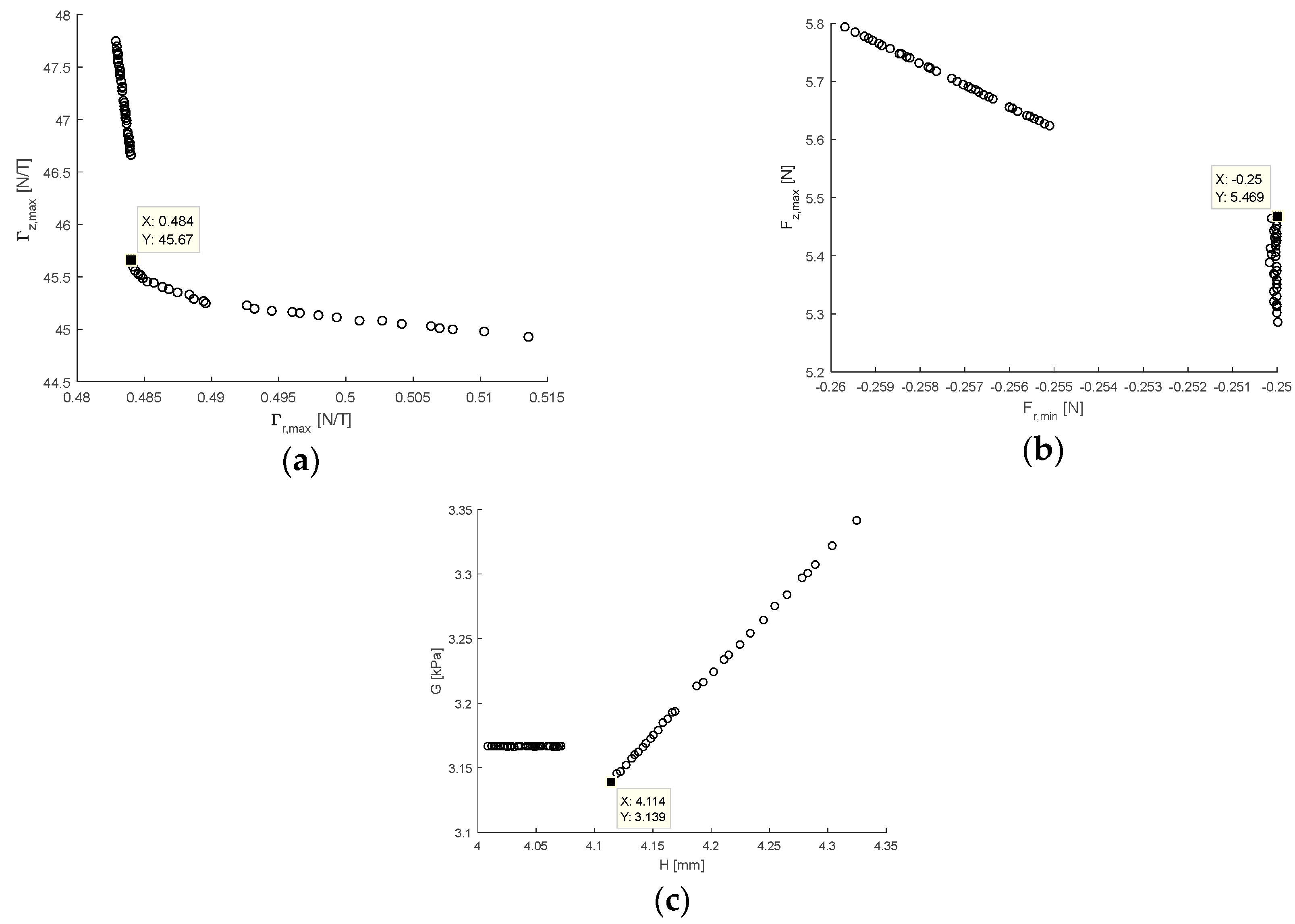

| Parameter | Value (Unit) |
|---|---|
| 4.97 (mm) | |
| 2 (mm) | |
| 6 (mm) | |
| 1 (mm) | |
| 6 (mm) | |
| 2.5 (mm) | |
| 2.97 (mm) | |
| 0.42 (rad) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boer, G.d.; Raske, N.; Wang, H.; Kow, J.; Alazmani, A.; Ghajari, M.; Culmer, P.; Hewson, R. Design Optimisation of a Magnetic Field Based Soft Tactile Sensor. Sensors 2017, 17, 2539. https://doi.org/10.3390/s17112539
Boer Gd, Raske N, Wang H, Kow J, Alazmani A, Ghajari M, Culmer P, Hewson R. Design Optimisation of a Magnetic Field Based Soft Tactile Sensor. Sensors. 2017; 17(11):2539. https://doi.org/10.3390/s17112539
Chicago/Turabian StyleBoer, Gregory de, Nicholas Raske, Hongbo Wang, Junwai Kow, Ali Alazmani, Mazdak Ghajari, Peter Culmer, and Robert Hewson. 2017. "Design Optimisation of a Magnetic Field Based Soft Tactile Sensor" Sensors 17, no. 11: 2539. https://doi.org/10.3390/s17112539
APA StyleBoer, G. d., Raske, N., Wang, H., Kow, J., Alazmani, A., Ghajari, M., Culmer, P., & Hewson, R. (2017). Design Optimisation of a Magnetic Field Based Soft Tactile Sensor. Sensors, 17(11), 2539. https://doi.org/10.3390/s17112539






