ABS-FishCount: An Agent-Based Simulator of Underwater Sensors for Measuring the Amount of Fish
Abstract
:1. Introduction
2. Related Work
2.1. Measurement of Fish and Their Properties
2.2. Multi-Agent Systems Related with Underwater Life
3. ABS-FishCount
- Fish agent: It represents a fish swimming in the water.
- Ecosystem agent: It simulates the creation and removal of fish in the ecosystem by spawning or destroying fish agents.
- Sensor agent: It represents an underwater sensor that can detect both fish and other underwater sensors in the nearby. It measures the amount of fish in the nearby. This measurement is intended to be overridden for obtaining different measurement strategies.
- Fish counter agent: This agent communicates with the underwater sensors through an underwater network. Its goal is to gather the information from all the sensor agents to provide an estimated measurement of the amount of fish in the monitored area.
- Water observer agent: This agent observes and saves the evolution of the simulation for later reporting it.
- Smart sensor agent: This agent extends the sensor agent to implement a smart way of measuring fish avoiding bias due to multiple detections of the same fish.
- Simple sensor agent: It extends the sensor agent to implement a basic way of measuring fish amount, and is used as control mechanism for the experimentation of the current work.
3.1. Subsystem of Underwater Life Simulation
3.2. Subsystem of Underwater Sensor Networks
3.3. Strategies of Underwater Sensors for Counting Fish
3.4. Implementation and User Interface
4. Experimentation
4.1. Experimentation Setup
4.2. Comparison of Simulation Evolutions
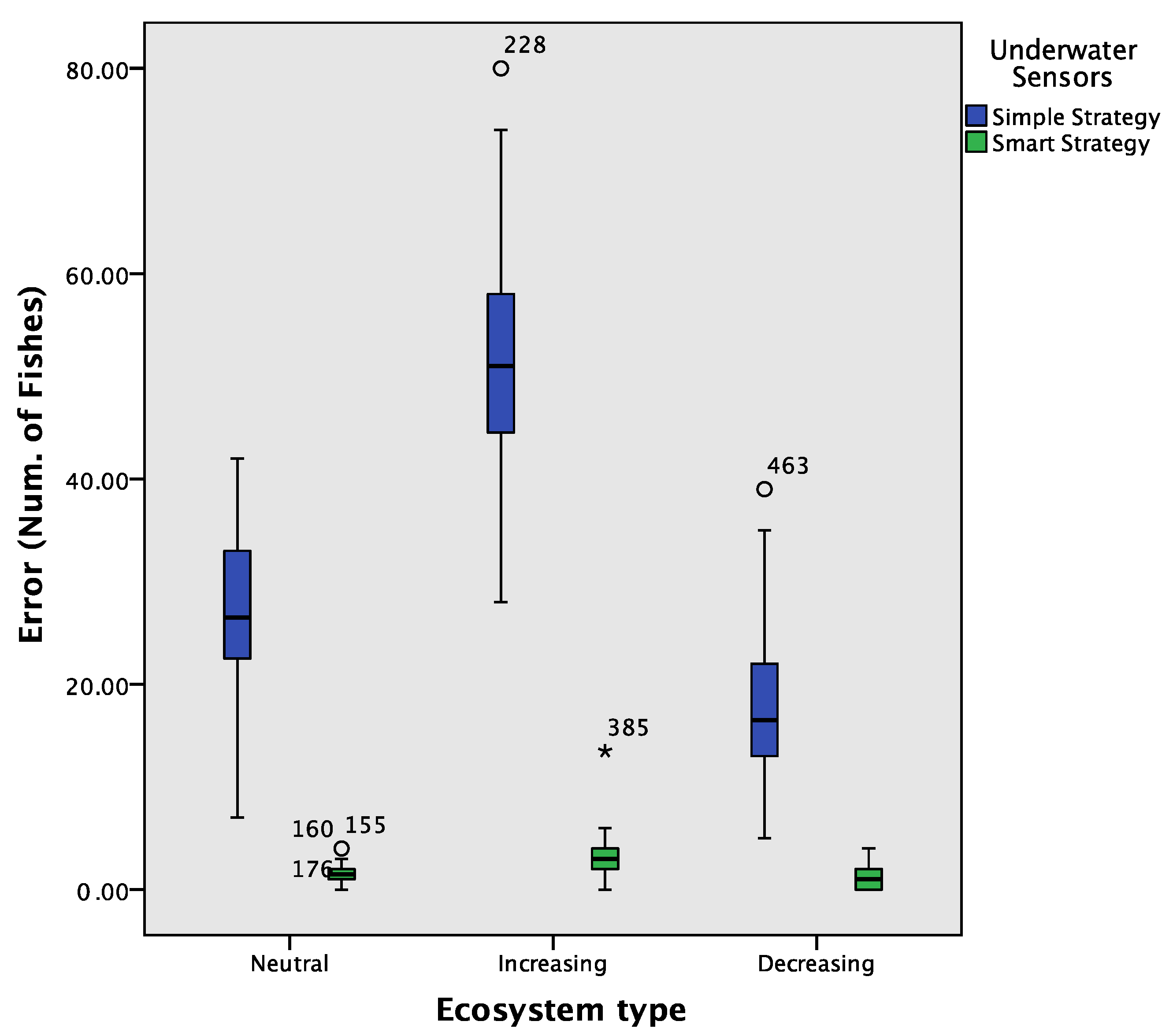
4.3. Comparison of Final Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lloret, J. Underwater sensor nodes and networks. Sensors 2013, 13, 11782–11796. [Google Scholar] [CrossRef] [PubMed]
- Akyildiz, I.F.; Pompili, D.; Melodia, T. Underwater acoustic sensor networks: Research challenges. Ad Hoc Netw. 2005, 3, 257–279. [Google Scholar] [CrossRef]
- Santos, R.; Orozco, J.; Micheletto, M.; Ochoa, S.F.; Meseguer, R.; Millan, P.; Molina, C. Real-Time Communication Support for Underwater Acoustic Sensor Networks. Sensors 2017, 17, 1629. [Google Scholar] [CrossRef] [PubMed]
- Das, A.P.; Thampi, S.M. Simulation tools for underwater sensor networks: A survey. Netw. Protoc. Algorithms 2017, 8, 41–55. [Google Scholar] [CrossRef]
- Kawahara, R.; Nobuhara, S.; Matsuyama, T. Dynamic 3D capture of swimming fish by underwater active stereo. Methods Oceanogr. 2016, 17, 118–137. [Google Scholar] [CrossRef]
- Schaner, T.; Fox, M.G.; Carolina Taraborelli, A. An inexpensive system for underwater video surveys of demersal fishes. J. Gt. Lakes Res. 2009, 35, 317–319. [Google Scholar] [CrossRef]
- Shinoda, R.; Wu, H.; Murata, M.; Ohnuki, H.; Yoshiura, Y.; Endo, H. Development of an optical communication type biosensor for real-time monitoring of fish stress. Sens. Actuators B Chem. 2017, 247, 765–773. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Z.; Dai, F.; Bu, Y.; Wang, H. Monocular Vision-Based Underwater Object Detection. Sensors 2017, 17, 1784. [Google Scholar] [CrossRef] [PubMed]
- Saberioon, M.; Cisar, P. Automated multiple fish tracking in three-dimension using a structured light sensor. Comput. Electron. Agric. 2016, 121, 215–221. [Google Scholar] [CrossRef]
- Pais, M.P.; Cabral, H.N. Fish behaviour effects on the accuracy and precision of underwater visual census surveys. A virtual ecologist approach using an individual-based model. Ecol. Model. 2017, 346, 58–69. [Google Scholar] [CrossRef]
- Burget, P.; Pachner, D. Fish farm automation. IFAC Proc. Vol. 2005, 38, 137–142. [Google Scholar] [CrossRef]
- Lloret, J.; Sendra, S.; Garcia, M.; Lloret, G. Group-based underwater wireless sensor network for marine fish farms. In Proceedings of the 2011 IEEE GLOBECOM Workshops (GC Wkshps), Houston, TX, USA, 5–9 December 2011; pp. 115–119. [Google Scholar]
- Simon, Y.; Levavi-Sivan, B.; Cahaner, A.; Hulata, G.; Antler, A.; Rozenfeld, L.; Halachmi, I. A behavioural sensor for fish stress. Aquac. Eng. 2017, 77, 107–111. [Google Scholar] [CrossRef]
- Petreman, I.C.; Jones, N.E.; Milne, S.W. Observer bias and subsampling efficiencies for estimating the number of migrating fish in rivers using Dual-frequency IDentification SONar (DIDSON). Fish. Res. 2014, 155, 160–167. [Google Scholar] [CrossRef]
- Negahdaripour, S.; Firoozfam, P.; Sabzmeydani, P. On processing and registration of forward-scan acoustic video imagery. In Proceedings of the 2nd Canadian Conference on Computer and Robot Vision, Victoria, BC, Canada, 9–11 May 2005; pp. 452–459. [Google Scholar]
- Garcia, M.; Sendra, S.; Lloret, G.; Lloret, J. Monitoring and control sensor system for fish feeding in marine fish farms. IET Commun. 2011, 5, 1682–1690. [Google Scholar] [CrossRef]
- Lloret, G.; Lloret, J. Simulator software for marine fish farms sustainability. WSEAS Trans. Environ. Dev. 2007, 3, 214–222. [Google Scholar]
- Lloret, J.; Garcia, M.; Sendra, S.; Lloret, G. An underwater wireless group-based sensor network for marine fish farms sustainability monitoring. Telecommun. Syst. 2015, 60, 67–84. [Google Scholar] [CrossRef]
- Bharamagoudra, M.R.; Manvi, S.S.; Gonen, B. Event driven energy depth and channel aware routing for underwater acoustic sensor networks: Agent oriented clustering based approach. Comput. Electr. Eng. 2017, 58, 1–19. [Google Scholar] [CrossRef]
- Gallehdari, Z.; Meskin, N.; Khorasani, K. Distributed reconfigurable control strategies for switching topology networked multi-agent systems. ISA Trans. 2017, 71, 51–67. [Google Scholar] [CrossRef] [PubMed]
- Jurdak, R.; Elfes, A.; Kusy, B.; Tews, A.; Hu, W.; Hernandez, E.; Kottege, N.; Sikka, P. Autonomous surveillance for biosecurity. Trends Biotechnol. 2015, 33, 201–207. [Google Scholar] [CrossRef] [PubMed]
- García-Magariño, I.; Plaza, I. FTS-SOCI: An agent-based framework for simulating teaching strategies with evolutions of sociograms. Simul. Model. Pract. Theory 2015, 57, 161–178. [Google Scholar] [CrossRef]
- Cooke, S.J.; Brownscombe, J.W.; Raby, G.D.; Broell, F.; Hinch, S.G.; Clark, T.D.; Semmens, J.M. Remote bioenergetics measurements in wild fish: Opportunities and challenges. Comp. Biochem. Physiol. Part A Mol. Integr. Physiol. 2016, 202, 23–37. [Google Scholar] [CrossRef] [PubMed]
- García, M.R.; Cabo, M.L.; Herrera, J.R.; Ramilo-Fernández, G.; Alonso, A.A.; Balsa-Canto, E. Smart sensor to predict retail fresh fish quality under ice storage. J. Food Eng. 2017, 197, 87–97. [Google Scholar] [CrossRef]
- Tušer, M.; Frouzová, J.; Balk, H.; Muška, M.; Mrkvička, T.; Kubečka, J. Evaluation of potential bias in observing fish with a DIDSON acoustic camera. Fish. Res. 2014, 155, 114–121. [Google Scholar] [CrossRef]
- Rakowitz, G.; Tušer, M.; Říha, M.; Juza, T.; Balk, H.; Kubečka, J. Use of high-frequency imaging sonar (DIDSON) to observe fish behaviour towards a surface trawl. Fish. Res. 2012, 123, 37–48. [Google Scholar] [CrossRef]
- Cenek, M.; Franklin, M. An adaptable agent-based model for guiding multi-species Pacific salmon fisheries management within a SES framework. Ecol. Model. 2017, 360, 132–149. [Google Scholar] [CrossRef]
- Gao, L.; Hailu, A. Evaluating the effects of area closure for recreational fishing in a coral reef ecosystem: The benefits of an integrated economic and biophysical modeling. Ecol. Econ. 2011, 70, 1735–1745. [Google Scholar] [CrossRef]
- Pereira, A.; Duarte, P.; Reis, L.P. Agent-based simulation of ecological models. In Proceedings of the 5th Workshop on Agent-Based Simulation, Lisbon, Portugal, 3–5 May 2004. [Google Scholar]
- Helbing, D.; Balietti, S. From social simulation to integrative system design. Eur. Phys. J. Spec. Top. 2011, 195, 69–100. [Google Scholar] [CrossRef]
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. ACM SIGGRAPH Comput. Graph. 1987, 21, 25–34. [Google Scholar] [CrossRef]
- Beltran, R.S.; Testa, J.W.; Burns, J.M. An agent-based bioenergetics model for predicting impacts of environmental change on a top marine predator, the Weddell seal. Ecol. Model. 2017, 351, 36–50. [Google Scholar] [CrossRef]
- Berman, M.; Nicolson, C.; Kofinas, G.; Tetlichi, J.; Martin, S. Adaptation and sustainability in a small arctic community: Results of an agent-based simulation model. Arctic 2004, 57, 401–414. [Google Scholar] [CrossRef]
- Kadir, H.A.; Arshad, M. Cooperative Multi Agent System for Ocean Observation System based on Consensus Algorithm. Procedia Comput. Sci. 2015, 76, 203–208. [Google Scholar] [CrossRef]
- Trygonis, V.; Georgakarakos, S.; Dagorn, L.; Brehmer, P. Spatiotemporal distribution of fish schools around drifting fish aggregating devices. Fish. Res. 2016, 177, 39–49. [Google Scholar] [CrossRef]
- De Kerckhove, D.T.; Milne, S.; Shuter, B.J. Measuring fish school swimming speeds with two acoustic beams and determining the angle of the school detection. Fish. Res. 2015, 172, 432–439. [Google Scholar] [CrossRef]
- García-Magariño, I.; Lacuesta, R.; Lloret, J. Source Code of the Agent-Based Simulator of Underwater Sensors for Measuring the Amount of Fishes Called ABS-FishCount. Mendeley Data, v1. 2017. Available online: http://dx.doi.org/10.17632/yzmt73x8j8.1 (accessed on 10 November 2017).
- Cossentino, M.; Gaud, N.; Hilaire, V.; Galland, S.; Koukam, A. ASPECS: An agent-oriented software process for engineering complex systems. Auton. Agents Multi-Agent Syst. 2010, 20, 260–304. [Google Scholar] [CrossRef]
- García-Magariño, I.; Palacios-Navarro, G.; Lacuesta, R. TABSAOND: A technique for developing agent-based simulation apps and online tools with nondeterministic decisions. Simul. Model. Pract. Theory 2017, 77, 84–107. [Google Scholar] [CrossRef]
- Wolff, L.M.; Badri-Hoeher, S. Imaging sonar-based fish detection in shallow waters. In Proceedings of the 2014 Oceans, St. John’s, NL, Canada, 14–19 September 2014; pp. 1–6. [Google Scholar]
- García-Magariño, I.; Gómez-Rodríguez, A.; González-Moreno, J.C.; Palacios-Navarro, G. PEABS: A process for developing efficient agent-based simulators. Eng. Appl. Artif. Intell. 2015, 46, 104–112. [Google Scholar] [CrossRef]
- Song, G.S. Water dams scanned by sidescan sonar. Sea Technol. 2005, 46, 57–60. [Google Scholar]
- Vaganay, J.; Leonard, J.J.; Curcio, J.A.; Willcox, J.S. Experimental validation of the moving long base-line navigation concept. In Proceedings of the 2004 IEEE/OES Autonomous Underwater Vehicles, Sebasco, ME, USA, 17–18 June 2004; pp. 59–65. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Earlbaum Associates: Hillsdale, NJ, USA, 1988. [Google Scholar]
- Rosenthal, J.A. Qualitative descriptors of strength of association and effect size. J. Soc. Serv. Res. 1996, 21, 37–59. [Google Scholar] [CrossRef]







| Neutral | Increasing | Decreasing | |
|---|---|---|---|
| Initial number of fish | 100 | 15 | 250 |
| Number of columns of underwater sensors | 4 | 4 | 4 |
| Number of rows of underwater sensors | 6 | 6 | 6 |
| Ecosystem probability of increasing fish per day | 0.30 | 0.75 | 0.25 |
| Ecosystem probability of decreasing fish per day | 0.30 | 0.25 | 0.75 |
| Duration of simulation (days) | 365 | 365 | 365 |
| Statistic | df1 | df2 | Sig. | |
|---|---|---|---|---|
| Welch | 977.017 | 1 | 305.170 | 0.000 ** |
| Brown–Forsythe | 977.017 | 1 | 305.170 | 0.000 ** |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Magariño, I.; Lacuesta, R.; Lloret, J. ABS-FishCount: An Agent-Based Simulator of Underwater Sensors for Measuring the Amount of Fish. Sensors 2017, 17, 2606. https://doi.org/10.3390/s17112606
García-Magariño I, Lacuesta R, Lloret J. ABS-FishCount: An Agent-Based Simulator of Underwater Sensors for Measuring the Amount of Fish. Sensors. 2017; 17(11):2606. https://doi.org/10.3390/s17112606
Chicago/Turabian StyleGarcía-Magariño, Iván, Raquel Lacuesta, and Jaime Lloret. 2017. "ABS-FishCount: An Agent-Based Simulator of Underwater Sensors for Measuring the Amount of Fish" Sensors 17, no. 11: 2606. https://doi.org/10.3390/s17112606
APA StyleGarcía-Magariño, I., Lacuesta, R., & Lloret, J. (2017). ABS-FishCount: An Agent-Based Simulator of Underwater Sensors for Measuring the Amount of Fish. Sensors, 17(11), 2606. https://doi.org/10.3390/s17112606






