Three-Dimensional Shape Measurements of Specular Objects Using Phase-Measuring Deflectometry
Abstract
:1. Introduction
2. Principle
2.1. Fringe Reflection
2.1.1. Orthogonal Fringe
2.1.2. Crossed Fringe
2.1.3. Color Fringe
2.2. Phase Extraction
2.3. Geometric Calibration
2.4. Slope Integration
2.4.1. RBF-Based Method
2.4.2. Least-Squares Method
2.4.3. Transform-Based Method
2.4.4. Comparison
3. Improved Phase-Measuring Deflectometry
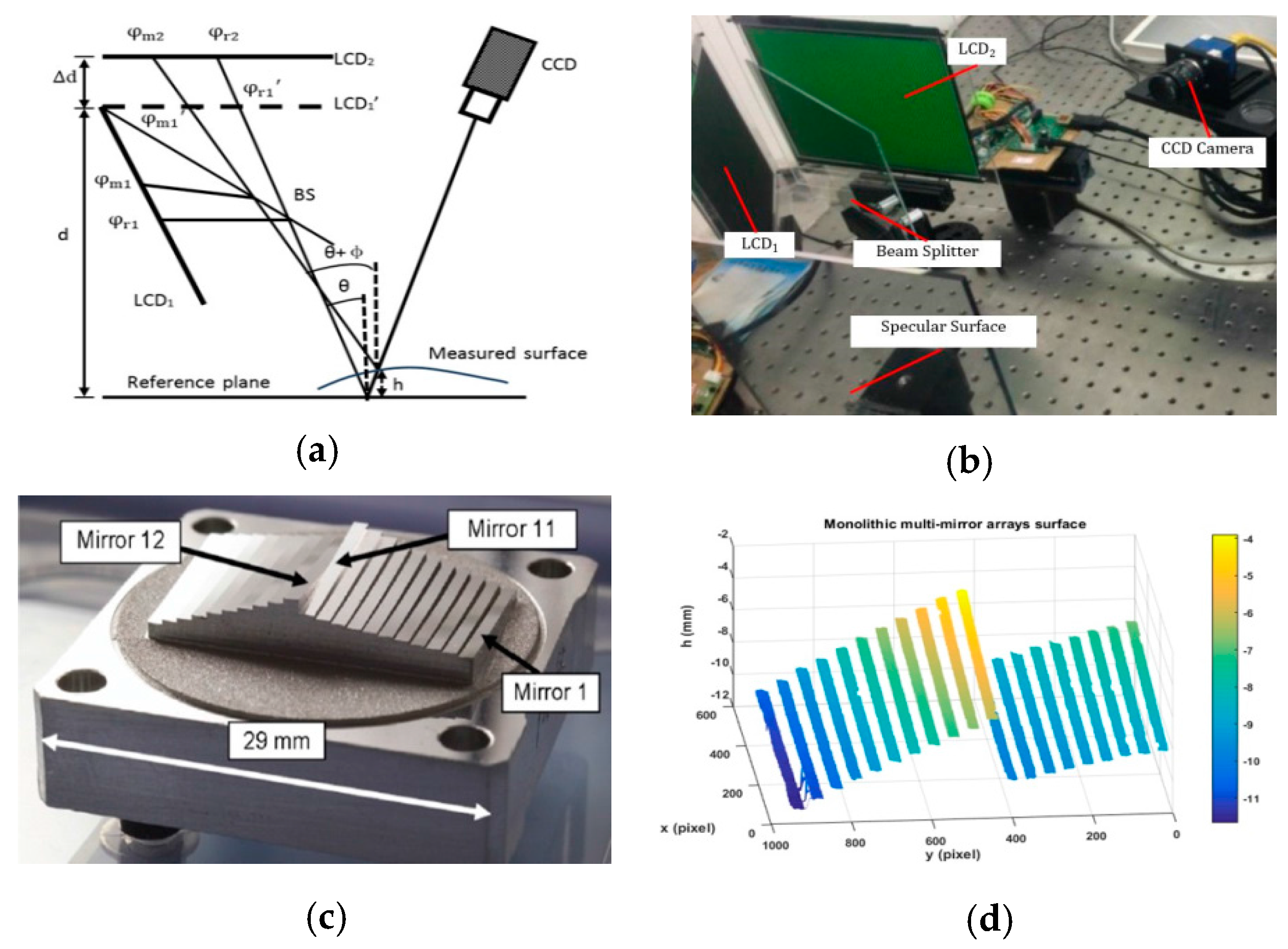
3.1. Direct Phase-Measuring Deflectometry (DPMD)
3.2. Model Phase-Measuring Deflectometry (MPMD)
4. Influential Factors on Measurement Results
4.1. Nonlinear Response of Display and Imaging Components
4.2. Display Screen
4.3. Slope Integration
4.4. Calibration
4.5. Phase Error
5. Future Directions
5.1. Invisible Light PMD
5.2. Discontinuous and Isolated Specular Surfaces
5.3. High Accuracy
5.4. Color Fringe
5.5. Real-Time Acquisition (Dynamic Specular Surface Measurement)
5.6. Portable
5.7. Partial Reflective Surface
5.8. Deflectometry Combining Interferometry
6. Application Fields
6.1. Aspherical and Spherical Mirrors
6.2. Automobile (Automotive Glass, Car Body)
6.3. Flaw Detection
6.4. Silicon Wafers and Ball Grid Array
6.5. Positioning of Specular Freeform Surface
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, F.; Brown, G.; Song, M. Overview of three-dimensional shape measurement using optical methods. Opt. Eng. 2000, 39, 10–22. [Google Scholar]
- Blais, F. Review of 20 years of range sensor development. J. Electron. Imaging 2004, 13, 231–240. [Google Scholar] [CrossRef]
- Gorthi, S.; Rastogi, P. Fringe projection techniques: Whither we are? Opt. Lasers Eng. 2010, 48, 134–140. [Google Scholar] [CrossRef]
- Zhang, S. Recent progresses on real-time 3D shape measurement using digital fringe projection techniques. Opt. Lasers Eng. 2010, 48, 149–158. [Google Scholar] [CrossRef]
- Salvi, J.; Fernandez, S.; Pribanic, T.; Llado, X. A state of the art in structured light patterns for surface profilometry. Pattern Recogn. 2010, 43, 2666–2680. [Google Scholar] [CrossRef]
- Zhang, Z. Review of single-shot 3D shape measurement by phase calculation-based fringe projection techniques. Opt. Lasers Eng. 2012, 50, 1097–1106. [Google Scholar] [CrossRef]
- Jeught, S.; Dirckx, J. Real-time structured light profilometry: a review. Opt. Laser Eng. 2016, 87, 18–31. [Google Scholar] [CrossRef]
- Zuo, C.; Huang, L.; Zhang, M.; Chen, Q.; Asundi, A. Temporal phase unwrapping algorithms for fringe projection profilometry: A comparative review. Opt. Laser Eng. 2016, 85, 84–103. [Google Scholar] [CrossRef]
- Zuo, C.; Chen, Q.; Gu, G.; Feng, S.; Feng, F. High-speed three-dimensional profilometry for multiple objects with complex shapes. Opt. Express 2012, 20, 19493–19510. [Google Scholar] [CrossRef] [PubMed]
- Mériaudeau, F.; Rantoson, R.; Fofi, D.; Stolz, C. Review and comparison of non-conventional imaging systems for three-dimensional digitization of transparent objects. J. Electron. Imaging 2012, 21, 21105. [Google Scholar] [CrossRef]
- Mansour, G. A developed algorithm for simulation of blades to reduce the measurement points and time on coordinate measuring machine (CMM). Measurement 2014, 54, 51–57. [Google Scholar] [CrossRef]
- Palousek, D.; Omasta, M.; Koutny, D.; Bednar, J.; Koutecky, T.; Dokoupil, F. Effect of matte coating on 3D optical measurement accuracy. Opt. Mater. 2015, 40, 1–9. [Google Scholar] [CrossRef]
- Xu, J.; Wang, P.; Yao, Y.; Liu, S.; Zhang, G. 3D multi-directional sensor with pyramid mirror and structured light. Opt. Laser Eng. 2017, 93, 156–163. [Google Scholar] [CrossRef]
- Pavlidis, G.; Koutsoudis, A.; Arnaoutoglou, F.; Tsioukas, V.; Chamzas, C. Methods for 3D digitization of cultural heritage. J. Cult. Herit. 2007, 8, 93–98. [Google Scholar] [CrossRef]
- Sansoni, G.; Trebeschi, M.; Docchio, F. State-of-The-Art and applications of 3D imaging sensors in industry, cultural heritage, medicine, and criminal investigation. Sensors 2009, 9, 568–601. [Google Scholar] [CrossRef] [PubMed]
- Wyant, J. White light interferometry. In Proceedings of the SPIE 4737, Orlando, FL, USA, 9 July 2002; Volume 4737. [Google Scholar]
- Jiang, X.; Wang, K.; Gao, F.; Muhamedsalih, H. Fast surface measurement using wavelength scanning interferometry with compensation of environmental noise. Appl. Opt. 2010, 49, 2903–2909. [Google Scholar] [CrossRef] [PubMed]
- Dávila, A. Wavelength scanning interferometry using multiple light sources. Opt. Express 2016, 24, 5311–5322. [Google Scholar] [CrossRef] [PubMed]
- Kafri, O.; Glatt, I. Moiré deflectometry: A ray deflection approach to optical testing. Opt. Eng. 1985, 24, 944–960. [Google Scholar] [CrossRef]
- Servin, M.; Rodriguez-Vera, R.; Carpio, M.; Morales, A. Automatic fringe detection algorithm used for moire deflectometry. Appl. Opt. 1990, 29, 3266–3270. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Luo, X.; Pfeifer, T.; Mischo, H. Moiré deflectometry based on Fourier-transform analysis. Measurement 1999, 25, 245–253. [Google Scholar] [CrossRef]
- Legarda-Saenz, R. Robust wavefront estimation using multiple directional derivatives in Moiré deflectometry. Opt. Laser Eng. 2007, 45, 915–921. [Google Scholar] [CrossRef]
- Lee, H.; Kim, S. Precision profile measurement of aspheric surfaces by improved Ronchi test. Opt. Eng. 1999, 38, 1041–1047. [Google Scholar] [CrossRef]
- Butel, G.; Smith, G.; Burge, J. Binary pattern deflectometry. Appl. Opt. 2014, 53, 923–930. [Google Scholar] [CrossRef] [PubMed]
- Knauer, M.; Kaminski, J.; Hausler, G. Phase measuring deflectometry: A new approach to measure specular free-form surfaces. Proceeding of the SPIE 5457, Strasbourg, France, 10 September 2004; Volume 4737. [Google Scholar]
- Häusler, G.; Richter, C.; Leitz, K.; Knauer, M. Microdeflectometry—A novel tool to acquire three-dimensional microtopography with nanometer height resolution. Opt. Lett. 2008, 33, 396–398. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Su, X.; Liu, Y.; Jing, H. 3D shape measurement of the aspheric mirror by advanced phase measuring deflectometry. Opt. Express 2008, 16, 15090–15096. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Feng, P.; Tao, T. Specular surface measurement by using least squares light tracking technique. Opt. Laser Eng. 2010, 48, 166–171. [Google Scholar] [CrossRef]
- Wedowski, R.; Atkinson, G.; Smith, M.; Smith, L. Dynamic deflectometry: A novel approach for the on-line reconstruction of specular freeform surfaces. Opt. Laser Eng. 2012, 50, 1765–1778. [Google Scholar] [CrossRef]
- Huang, L.; Ng, C.; Asundi, A. Fast full-field out-of-plane deformation measurement using fringe reflectometry. Opt. Laser Eng. 2012, 50, 529–533. [Google Scholar] [CrossRef]
- Schulz, M.; Ehret, G.; Fitzenreiter, A. Scanning deflectometric form measurement avoiding path-dependent angle measurement errors. J. Eur. Opt. Soc. Rap. Publ. 2010, 5, 10026. [Google Scholar] [CrossRef]
- Hao, Q.; Zhu, Q.; Wang, Y. Deflectometer with synthetically generated reference circle for aspheric surface testing. Opt. Laser Technol. 2005, 37, 375–380. [Google Scholar] [CrossRef]
- Krey, S.; van Amstel, W.D.; Szwedowicz, K.; Campos, J.; Moreno, A.; Lous, E. A fast optical scanning deflectometer for measuring the topography of large silicon wafers. In Proceedings of the SPIE 5523, Denver, CO, USA, 14 October 2004; Volume 559702. [Google Scholar]
- Van Amstel, W.D.; Bäumer, S.M.; Horijon, J.L. Optical figure testing by scanning deflectometry. In Proceedings of the SPIE 3782, Berlin, Germany, 6 September 1999; pp. 320–327. [Google Scholar]
- Miks, A.; Novak, J.; Novak, P. Method for reconstruction of shape of specular surfaces using scanning beam deflectometry. Opt. Lasers Eng. 2013, 51, 867–872. [Google Scholar] [CrossRef]
- Creath, K. Phase measurement interferometry techniques. Prog. Opt. 1988, 26, 349–393. [Google Scholar]
- Takeda, M.; Mutoh, K. Fourier transform profilometry for the automatic measurement of 3D object shapes. Appl. Opt. 1983, 22, 3977–3982. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; Chen, W. Fourier transform profilometry: A review. Opt. Lasers Eng. 2001, 35, 263–284. [Google Scholar] [CrossRef]
- Qian, K.; Wang, H.; Gao, W. Windowed Fourier transform for fringe pattern analysis: Theoretical analyses. Appl. Opt. 2008, 47, 5408–5419. [Google Scholar]
- Chen, W.; Su, X.; Cao, Y.; Zhang, Q.; Xiang, L. Method for eliminating zero spectrum in Fourier transform profilometry. Opt. Lasers Eng. 2005, 43, 1267–1276. [Google Scholar] [CrossRef]
- Zhong, J.; Weng, J. Spatial carrier-fringe pattern analysis by means of wavelet transform: Wavelet transform profilometry. Appl. Opt. 2004, 43, 4993–4998. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Wang, Z.; Pan, B.; Hoang, T.; Vo, M.; Luu, L. Two-dimensional continuous wavelet transform for phase determination of complex interferograms. Appl. Opt. 2011, 50, 2425–2430. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Qian, K.; Pan, B.; Asundi, A. Comparison of Fourier transform, windowed Fourier transform, and wavelet transform methods for phase extraction from a single fringe pattern in fringe projection profilometry. Opt. Lasers Eng. 2010, 48, 141–148. [Google Scholar] [CrossRef]
- Zhang, Z.; Jing, Z.; Wang, Z.; Kuang, D. Comparison of Fourier transform, windowed Fourier transform, and wavelet transform methods for phase calculation at discontinuities in fringe projection profilometry. Opt. Lasers Eng. 2012, 50, 1152–1160. [Google Scholar] [CrossRef]
- Petz, M.; Tutsch, R. Reflection grating photogrammetry: A technique for absolute shape measurement of specular free-form surfaces. Opt. Photon. 2005, 5869, 58691D. [Google Scholar]
- Guo, C.; Lin, X.; Hu, A.; Zou, J. Improved phase-measuring deflectometry for aspheric surfaces test. Appl. Opt. 2016, 55, 2059–2064. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Ng, C.; Asundi, A. Dynamic three-dimensional sensing for specular surface with monoscopic fringe reflectometry. Opt. Express 2011, 19, 12809–12814. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Olesch, E.; Yang, Z.; Häusler, G. Fast and accurate deflectometry with crossed fringes. Adv. Opt. Technol. 2014, 3, 441–445. [Google Scholar] [CrossRef]
- Xie, P.; Tang, M.; Wei, X. Three-dimensional shape measurement of specular surfaces by orthogonal composite fringe reflection. In Proceedings of the SPIE 8200, Beijing, China, 29 November 2011. [Google Scholar]
- Li, B.; Ma, S.; Zhai, Y. Fast temporal phase unwrapping method for the fringe reflection technique based on the orthogonal grid fringes. Appl. Opt. 2015, 54, 6282–6290. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Zhang, X.; Xu, M. Dynamic three-dimensional shape measurement for specular freeform surfaces with the quaternary orthogonal grid fringes. In Proceedings of the SPIE 155, Beijing, China, 19 October 2016. [Google Scholar]
- Liu, T.; Zhou, C.; Liu, Y.; Si, S.; Lei, Z. Deflectometry for phase retrieval using a composite fringe. Opt. Appl. 2014, 94, 451–461. [Google Scholar]
- Flores, J.; Bravo-Medina, B.; Ferrari, J. One-frame two-dimensional deflectometry for phase retrieval by addition of orthogonal fringe patterns. Appl. Opt. 2013, 52, 6537–6542. [Google Scholar] [CrossRef] [PubMed]
- Pfortner, A.; Schwider, J. Red-green-blue interferometer for the metrology of discontinuous structures. Appl. Opt. 2003, 42, 667–673. [Google Scholar] [CrossRef] [PubMed]
- Hausler, G.; Ritter, D. Parallel three-dimensional sensing by color-coded triangulation. Appl. Opt. 1993, 32, 7164–7169. [Google Scholar] [CrossRef] [PubMed]
- Huang, P.; Hu, Q.; Jin, F.; Chiang, F. Color-encoded digital fringe projection technique for high-speed three-dimensional surface contouring. Opt. Eng. 1999, 38, 1065–1071. [Google Scholar] [CrossRef]
- Skydan, O.; Lalor, M.; Burton, D. Technique for phase measurement and surface reconstruction by use colored structured light. Appl. Opt. 2002, 41, 6104–6117. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Towers, C.; Towers, D. Time efficient color fringe projection system for 3D shape and color using optimum 3-frequency selection. Opt. Express 2006, 14, 6444–6455. [Google Scholar] [CrossRef] [PubMed]
- Trumper, I.; Choi, H.; Kim, D. Instantaneous phase shifting deflectometry. Opt. Express 2016, 24, 27993–28007. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Yue, H.; Yi, J.; Li, M.; Liu, Y. Single-shot three-dimensional shape measurement of specular surfaces by orthogonal color fringe pattern reflection technique. In Proceedings of the SPIE/COS Photonics Asia, Beijing, China, 13 November 2014. [Google Scholar]
- Wu, Y.; Yue, H.; Yi, J.; Li, M.; Liu, Y. Dynamic specular surface measurement based on color-encoded fringe reflection technique. Opt. Eng. 2016, 55, 024104. [Google Scholar] [CrossRef]
- Ma, S.; Li, B. A phase retrieval algorithm based on color-frequency encoding for fringe reflection technique. In Proceedings of the Eighth International Symposium on Advanced Optical Manufacturing and Testing Technology, Suzhou, China, 27 September 2016. [Google Scholar]
- Tsai, R. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses. IEEE J. Robot Autom. 1987, 3, 323–344. [Google Scholar] [CrossRef]
- Salvi, J.; Armangué, X.; Batlle, J. A comparative review of camera calibrating methods with accuracy evaluation. Pattern Recogn. 2002, 35, 1617–1635. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern. Anal. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Xiao, Y.; Su, X.; Chen, W. Flexible geometrical calibration for fringe-reflection 3D measurement. Opt. Lett. 2012, 37, 620–622. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Gao, F.; Jiang, X. Iterative optimization calibration method for stereo deflectometry. Opt. Express 2015, 23, 22060–22068. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Chen, K.; Wei, H.; Li, Y. Improved system calibration for specular surface measurement by using reflections from a plane mirror. Appl. Opt. 2016, 55, 7018–7028. [Google Scholar] [CrossRef] [PubMed]
- Olesch, E.; Faber, C.; Häusler, G. Deflectometric Self-Calibration for Arbitrary Specular Surface. In Proceedings of the Fifth International Conference on Optical and Photonics Engineering, Singapore, 13 June 2017. [Google Scholar]
- E, K.; Li, D.; Yang, L.; Guo, G.; Li, M.; Wang, X.; Zhang, T.; Xiong, Z. Novel method for high accuracy figure measurement of optical flat. Opt. Lasers Eng. 2017, 88, 162–166. [Google Scholar] [CrossRef]
- Xiao, Y.; Su, X.; You, Z. Pose transfer geometrical calibration for fringe-reflection optical three-dimensional measurement. Opt. Commun. 2013, 305, 143–146. [Google Scholar] [CrossRef]
- Yuan, T.; Zhang, F.; Tao, X.; Zhang, X.; Zhou, R. Flexible geometrical calibration for fringe-reflection optical three-dimensional shape measurement. Appl. Opt. 2015, 54, 9102–9107. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Idir, M.; Zuo, C.; Kaznatcheev, K.; Zhou, L.; Asundi, A. Comparison of two-dimensional integration methods for shape reconstruction from gradient data. Opt. Lasers Eng. 2015, 64, 1–11. [Google Scholar] [CrossRef]
- Ettl, S.; Kanimski, J.; Knauer, M.; Häusler, G. Shape reconstruction from gradient data. Appl. Opt. 2008, 47, 2091–2097. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Gao, F.; Jiang, X. Least-squares method for data reconstruction from gradient data in deflectometry. Appl. Opt. 2016, 55, 6052–6059. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Asundi, A. Framework for gradient integration by combining radial basis functions method and least-squares method. Appl. Opt. 2013, 52, 6016–6021. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Li, Y.; Liu, K.; Ma, X.; Wang, H. Improving wavefront reconstruction accuracy by using integration equations with higher order truncation errors in the Southwell geometry. J. Opt. Soc. Am. A 2013, 30, 1448–1459. [Google Scholar] [CrossRef] [PubMed]
- Guang, H.; Wang, Y.; Zhang, L.; Li, L.; Li, M.; Ji, L. Enhancing wavefront estimation accuracy by using higher-order iterative compensations in the Southwell configuration. Appl. Opt. 2017, 56, 2060–2067. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Gao, F.; Jiang, X. Improvement of high-order least-squares integration method for stereo deflectometry. Appl. Opt. 2015, 54, 10249–10255. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Asundi, A. Improvement of least-squares integration method with iterative compensations in fringe reflectometry. Appl. Opt. 2012, 51, 7459–7465. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.-L.; Li, S.; Zhang, Q.; Zhong, J.; Su, X.; You, Z. Optical fringe-reflection deflectometry with sparse representation. Opt. Lasers Eng. 2017, in press. [Google Scholar] [CrossRef]
- Huang, L.; Xue, J.; Gao, B.; Zuo, C.; Idir, M. Spline based least squares integration for two-dimensional shape or wavefront reconstruction. Opt. Laser Eng. 2017, 91, 221–226. [Google Scholar] [CrossRef]
- Li, M.; Li, D.; Jin, C.; E, K.; Yuan, X.; Xiong, Z.; Wang, Q. Improved zonal integration method for high accurate surface reconstruction in quantitative deflectometry. Appl. Opt. 2017, 56, F144–F151. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Xue, J.; Gao, B.; Zuo, C.; Idir, M. Zonal wavefront reconstruction in quadrilateral geometry for phase measuring deflectometry. Appl. Opt. 2017, 56, 5139–5144. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Chen, K.; Wei, H.; Li, Y. Improved method for rapid shape recovery of large specular surfaces based on phase measuring deflectometry. Appl. Opt. 2016, 55, 2760–2770. [Google Scholar] [CrossRef] [PubMed]
- Freischlad, K.; Koliopoulos, C. Modal estimation of a wave front from difference measurements using the discrete Fourier transform. J. Opt. Soc. Am. A 1986, 3, 1852–1861. [Google Scholar] [CrossRef]
- Roddier, F.; Roddier, C. Wave front reconstruction using iterative Fourier transforms. Appl. Opt. 1991, 30, 1325–1327. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Wang, Z. Wave front reconstruction using iterative discrete Fourier transforms with fried geometry. Optik 2006, 117, 77–81. [Google Scholar] [CrossRef]
- Poyneer, L.; Gavel, D.; Brase, J. Fast wavefront reconstruction in large adaptive optics systems with use of the Fourier transform. J. Opt. Soc. Am. A 2002, 19, 2100–2111. [Google Scholar] [CrossRef]
- Zou, W.; Rolland, J. Iterative zonal wavefront estimation algorithm for optical testing with general-shaped pupils. J. Opt. Soc. Am. A 2005, 22, 938–951. [Google Scholar] [CrossRef]
- Talmi, A.; Ribak, E. Wavefront reconstruction from its gradients. J. Opt. Soc. Am. A 2006, 23, 288–297. [Google Scholar] [CrossRef]
- Li, W.; Bothe, T.; Kopylow, C.; Juptner, W. Evaluation methods for gradient measurement techniques. In Proceedings of the Photonics Europe, Strasbourg, France, 10 September 2004. [Google Scholar]
- Li, W.; Sandner, M.; Gesierich, A.; Burke, J. Absolute optical surface measurement with deflectometry. In Proceedings of the SPIE Optical Engineering + Applications, San Diego, CA, USA, 13 September 2012. [Google Scholar]
- Yue, H.; Wu, Y.; Zhao, B.; Ou, Z.; Liu, Y.; Liu, Y. A carrier removal method in phase measuring deflectometry based on the analytical carrier phase description. Opt. Express 2013, 21, 21756–21765. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Su, X.; Chen, W.; Liu, Y. Three-dimensional shape measurement of aspheric mirrors with fringe reflection photogrammetry. Appl. Opt. 2012, 51, 457–464. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Su, X.; Wu, F.; Liu, Y. A novel phase measuring deflectometry for aspheric mirror test. Opt. Express 2009, 17, 19778–19784. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Su, X.; Liu, Y.; Zhang, Q. Testing an aspheric mirror based on phase measuring deflectometry. Opt. Eng. 2009, 48, 103603. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, S.; Zhang, Z.; Gao, N.; Gao, F.; Jiang, X. Full-field 3D shape measurement of discontinuous specular objects by direct phase measuring deflectometry. Sci. Rep. 2017, 7, 10293. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Huang, S.; Gao, N.; Gao, F.; Jiang, X. Full-field 3D shape measurement of specular object having discontinuous surfaces. In Proceedings of the Fifth International Conference on Optical and Photonics Engineering, Singapore, 13 June 2017. [Google Scholar]
- Zhang, Z.; Liu, Y.; Huang, S.; Niu, Z.; Guo, J.; Gao, N. Full-field 3D shape measurement of specular surfaces by direct phase to depth relationship. In Proceedings of the SPIE/COS Photonics Asia, Beijing, China, 24 November 2016. [Google Scholar]
- Zhao, P.; Gao, N.; Zhang, Z.; Gao, F.; Jiang, X. Performance analysis and evaluation of direct phase measuring deflectometry. Opt. Lasers Eng. 2018, 103, 24–33. [Google Scholar] [CrossRef]
- Huang, L.; Xue, J.; Gao, B.; Mcpherson, C.; Beverage, J.; Idir, M. Modal phase measuring deflectometry. Opt. Express 2016, 24, 24649–24664. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Xue, J.; Gao, B.; Idir, M. Three-dimensional shape measurement with phase measuring deflectometry. In Proceedings of the Fifth International Conference on Optical and Photonics Engineering, Singapore, 13 June 2017. [Google Scholar]
- Huang, L.; Xue, J.; Gao, B.; Mcpherson, C.; Beverage, J.; Idir, M. Model mismatch analysis and compensation for modal phase measuring deflectometry. Opt. Express 2017, 25, 881–887. [Google Scholar] [CrossRef] [PubMed]
- Shore, P.; Morantz, P.; Lee, D.; McKeown, P. Manufacturing and measurement of the MIRI spectrometer optics for the James Webb space telescope. CIRP Ann-Manuf. Technol. 2006, 55, 543–546. [Google Scholar] [CrossRef]
- Peng, J.; Liu, X.; Deng, D.; Guo, H.; Cai, Z.; Peng, X. Suppression of projector distortion in phase-measuring profilometry by projecting adaptive fringe patterns. Opt. Express 2016, 24, 21846–21860. [Google Scholar] [CrossRef] [PubMed]
- Cai, Z.; Liu, X.; Peng, X.; Zhang, Z.; Jiang, H.; Yin, Y. Phase error compensation methods for high-accuracy profile measurement. Meas. Sci. Technol. 2016, 27, 045201. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, X.; Jiang, H.; He, D.; Peng, X.; Huang, S. Flexible phase error compensation based on Hilbert transform in phase shifting profilometry. Opt. Express 2015, 23, 25171–25181. [Google Scholar] [CrossRef] [PubMed]
- Lei, S.; Zhang, S. Flexible 3-D shape measurement using projector defocusing. Opt. Lett. 2009, 34, 3080–3082. [Google Scholar] [CrossRef] [PubMed]
- Olesch, E.; Häusler, G.; W¨ornlein, A.; Stinzing, F.; Eldik, C. Deflectometric measurement of large mirrors. Adv. Opt. Technol. 2014, 3, 335–343. [Google Scholar] [CrossRef]
- Fischer, M.; Petz, M.; Tutsch, R. Evaluation of LCD monitors for deflectometric measurement systems. In Proceedings of the SPIE Photonics Europe, Brussels, Belgium, 14 May 2010. [Google Scholar]
- Ritter, R. Deformation measurement by optical field methods in material testing and for verification of numerical simulation. In Proceedings of the International Conference on Applied Optical Metrology, Balatonfured, Hungary, 29 September 1998; pp. 24–33. [Google Scholar]
- Maestro-Watson, D.; Izaguirre, A.; Arana-Arexolaleiba, N. LCD screen calibration for deflectometric systems considering a single layer refraction model. In Proceedings of the IEEE International Workshop of Electronics, Control, Measurement, Signals and their Application to Mechatronics (ECMSM) 2017, Donostia-San Sebastian, Spain, 24–26 May 2017. [Google Scholar]
- Wu, Y.; Yue, H.; Yi, J.; Li, M.; Liu, Y. Phase error analysis and reduction in phase measuring deflectometry. Opt. Eng. 2015, 54, 064103. [Google Scholar] [CrossRef]
- Höfer, S.; Burke, J.; Heizmann, M. Infrared deflectometry for the inspection of diffusely specular surfaces. Adv. Opt. Technol. 2016, 5, 377–387. [Google Scholar] [CrossRef]
- Na, S.; Shin, S.; Kim, D.; Yu, Y. Deflectometric measurement of a fine metal mask by using near infrared to reduce scattering. New Phys. Sae Mulli 2016, 66, 108–113. [Google Scholar] [CrossRef]
- Kim, D.; Su, T.; Su, P.; Oh, C.; Graves, L.; Burge, J. Accurate and rapid IR metrology for the manufacture of freeform optics. SPIE Newsroom 2015. [Google Scholar] [CrossRef]
- Sprenger, D.; Faber, C.; Seraphim, M.; Häusler, G. UV-Deflectometry: No Parasitic Reflections. Available online: http://www.optik.uni-erlangen.de/fileadmin/leuchs/leuchs-uni/osmin/papers/2010/2010_243T_GH_UV-Deflectometry_2010.pdf (accessed on 5 December 2017).
- Zhang, H.; Ji, L.; Liu, S.; Li, S.; Han, S.; Zhang, X. Three-dimensional shape measurement of a highly reflected, specular surface with structured light method. Appl. Opt. 2012, 51, 7724–7732. [Google Scholar] [CrossRef] [PubMed]
- Padilla, M.; Servin, M.; Garnica, G. Fourier analysis of RGB fringe-projection profilometry and robust phase-demodulation methods against crosstalk distortion. Opt. Express 2016, 24, 15417–15428. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Wong, J.; Asundi, A. Specular 3D shape measurement with a compact fringe reflection system. In Proceedings of the International Conference on Optics in Precision Engineering and Nanotechnology, Singapore, 22 June 2013. [Google Scholar]
- Butel, G.; Smith, G.; Burge, J. Deflectometry using portable devices. Opt. Eng. 2015, 54, 025111. [Google Scholar] [CrossRef]
- Maldonado, A.; Su, P.; Burge, J. Development of a portable deflectometry system for high spatial resolution surface measurements. Appl. Opt. 2014, 53, 4023–4032. [Google Scholar] [CrossRef] [PubMed]
- Röttinger, C.; Faber, C.; Olesch, E.; Häusler, G.; Kurz, M.; Uhlmann, E. Deflectometry for Ultra Precision Machining—Measuring without Rechecking. Available online: www.dgao-proceedings.de/download/112/112_p28.pdf (accessed on 3 November 2017).
- Skydan, O.; Lalor, M.; Burton, D. Three-dimensional shape measurement of non-full-field reflective surfaces. Appl. Opt. 2005, 44, 4745–4752. [Google Scholar] [CrossRef] [PubMed]
- Skydan, O.; Lalor, M.; Burton, D. 3D shape measurement of automotive glass by using a fringe reflection technique. Meas. Sci. Technol. 2007, 18, 106–114. [Google Scholar] [CrossRef]
- Zhang, X.; North, W. Retroreflective grating analysis versus physical measurements of surface contour. Opt. Eng. 1998, 37, 1464–1467. [Google Scholar] [CrossRef]
- Zhang, X.; North, W. Retroreflective projection gratings. Opt. Laser Technol. 1998, 31, 369–371. [Google Scholar] [CrossRef]
- Faber, C.; Olesch, E.; Krobot, R.; Häusler, G. Deflectometry challenges interferometry: The competition gets tougher! In Proceedings of the SPIE Optical Engineering + Applications, San Diego, CA, USA, 13 September 2012. [Google Scholar]
- Häusler, G.; Faber, C.; Olesch, E.; Ettl, S. Deflectometry vs. Interferometry. In Proceedings of the Optical Measurement Systems for Industrial Inspection VIII, Munich, Germany, 13 May 2013. [Google Scholar]
- Hanayama, R. A trial for a reliable shape measurement using interferometry and deflectometry. In Proceedings of the SPIE Optical Engineering + Applications, San Diego, CA, USA, 18 August 2014. [Google Scholar]
- Tang, Y.; Su, X.; Hu, S. Measurement based on fringe reflection for testing aspheric optical axis precisely and flexibly. Appl. Opt. 2011, 50, 5944–5948. [Google Scholar] [CrossRef] [PubMed]
- Su, P.; Wang, Y.; Burge, J.; Kaznatcheev, K.; Idir, M. Non-null full field X-ray mirror metrology using SCOTS: A reflection deflectometry approach. Opt. Express 2012, 20, 12393–12406. [Google Scholar] [CrossRef] [PubMed]
- Fang, F.; Zhang, X.; Weckenmann, A.; Zhang, G.; Evans, C. Manufacturing and measurement of freeform optics. CIRP Ann-Manuf. Technol. 2013, 62, 823–846. [Google Scholar] [CrossRef]
- Höfling, R.; Aswendt, P.; Neugebauer, R. Phase reflection-A new solution for the detection of shape defects on car body sheets. Opt. Eng. 2000, 39, 175–182. [Google Scholar] [CrossRef]
- Xu, J.; Xi, N.; Zhang, C.; Shi, Q.; Gregory, J. A geometry and optical property inspection system for automotive glass based on fringe patterns. Opt. Appl. 2010, 40, 827–841. [Google Scholar]
- Hung, M.; Shang, H. Nondestructive testing of specularly reflective objects using reflection three-dimensional computer vision technique. Opt. Eng. 2003, 42, 1343–1347. [Google Scholar]
- Chan, F. Reflective fringe pattern technique for subsurface crack detection. NDT E Int. 2008, 41, 602–610. [Google Scholar] [CrossRef]
- Kammel, S.; Leon, F. Deflectometric measurement of specular surfaces. IEEE Trans. Instrum. Meas. 2008, 57, 763–769. [Google Scholar] [CrossRef]
- Song, Z.; Chung, R.; Zhang, X.-T. An accurate and robust strip-edge-based structured light means for shiny surface micromeasurement in 3-D. IEEE Trans. Instrum. Electron. 2013, 60, 1023–1032. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, L.; Zhang, G. Novel method of positioning optical freeform surfaces based on fringe deflectometry. CIRP Ann-Manuf. Technol. 2017, 66, 507–510. [Google Scholar] [CrossRef]





| Orthogonal Fringe | Crossed Fringe | Color Fringe | |
|---|---|---|---|
| Time | Long | Short | Shortest |
| Accuracy | High | Median | Low |
| Resolution | High | Median | High |
| RBF-Based | Least-Squares | Transform-Based | |
|---|---|---|---|
| Speed | Slow | Fast for small size Very slow for huge size | Fast |
| Accuracy | High (sub-micrometer) | High (sub-micrometer) | Median (micrometer) |
| Memory | Huge for large size | Small | Large |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Wang, Y.; Huang, S.; Liu, Y.; Chang, C.; Gao, F.; Jiang, X. Three-Dimensional Shape Measurements of Specular Objects Using Phase-Measuring Deflectometry. Sensors 2017, 17, 2835. https://doi.org/10.3390/s17122835
Zhang Z, Wang Y, Huang S, Liu Y, Chang C, Gao F, Jiang X. Three-Dimensional Shape Measurements of Specular Objects Using Phase-Measuring Deflectometry. Sensors. 2017; 17(12):2835. https://doi.org/10.3390/s17122835
Chicago/Turabian StyleZhang, Zonghua, Yuemin Wang, Shujun Huang, Yue Liu, Caixia Chang, Feng Gao, and Xiangqian Jiang. 2017. "Three-Dimensional Shape Measurements of Specular Objects Using Phase-Measuring Deflectometry" Sensors 17, no. 12: 2835. https://doi.org/10.3390/s17122835
APA StyleZhang, Z., Wang, Y., Huang, S., Liu, Y., Chang, C., Gao, F., & Jiang, X. (2017). Three-Dimensional Shape Measurements of Specular Objects Using Phase-Measuring Deflectometry. Sensors, 17(12), 2835. https://doi.org/10.3390/s17122835






