Optimal Power Allocation of Relay Sensor Node Capable of Energy Harvesting in Cooperative Cognitive Radio Network
Abstract
:1. Introduction
- (1)
- Energy harvesting in combination with power superposition coding, both performed by the ST for the CC scheme, is herein considered for the first time. The outage probabilities of the PN and the SN, according to the power splitting ratio and the power sharing coefficient, are assessed by numerical analysis and Monte-Carlo simulation. The relay network presented by Huang et al. [28] also deals with optimal power allocation. However, their work did not involve an SR in the secondary network, whereas ours takes the SR into consideration for optimal power allocation. The optimal power allocation schemes in [29,30] are in relation to relay selection, unlike ours, which employs a single relay sensor to execute power superposition coding.
- (2)
- The jointly optimal power splitting ratio and power sharing coefficient were found using specific analytical or mathematical expressions. In these expressions, the impact of the system parameters (including the two power parameters) on the outage probabilities are evaluated.
- (3)
- The range of the power sharing coefficient that could provide an outage probability of the PN lower than the one obtained by direct transmission from the PT to the PR is identified. Other new findings are presented in the figures in Section 4. The rest of this paper is organized as follows. In Section 2, a system model corresponding to the proposed scheme is described. In Section 3, the analytical or mathematical expressions are derived that will be used to determine the outage probabilities of the PN and the SN according to the power splitting ratio and the power sharing coefficient. Section 4 presents the performance evaluation, according to the two power parameters. Section 5 concludes the paper.
2. System Model
2.1. System Operation in Two Phases
2.2. SNRs and SINRs of Signals
3. Outage Probability Analysis
3.1. Outage Probability of PN
3.2. Outage Probability of the SN
4. Numerical Analysis and Simulation Results
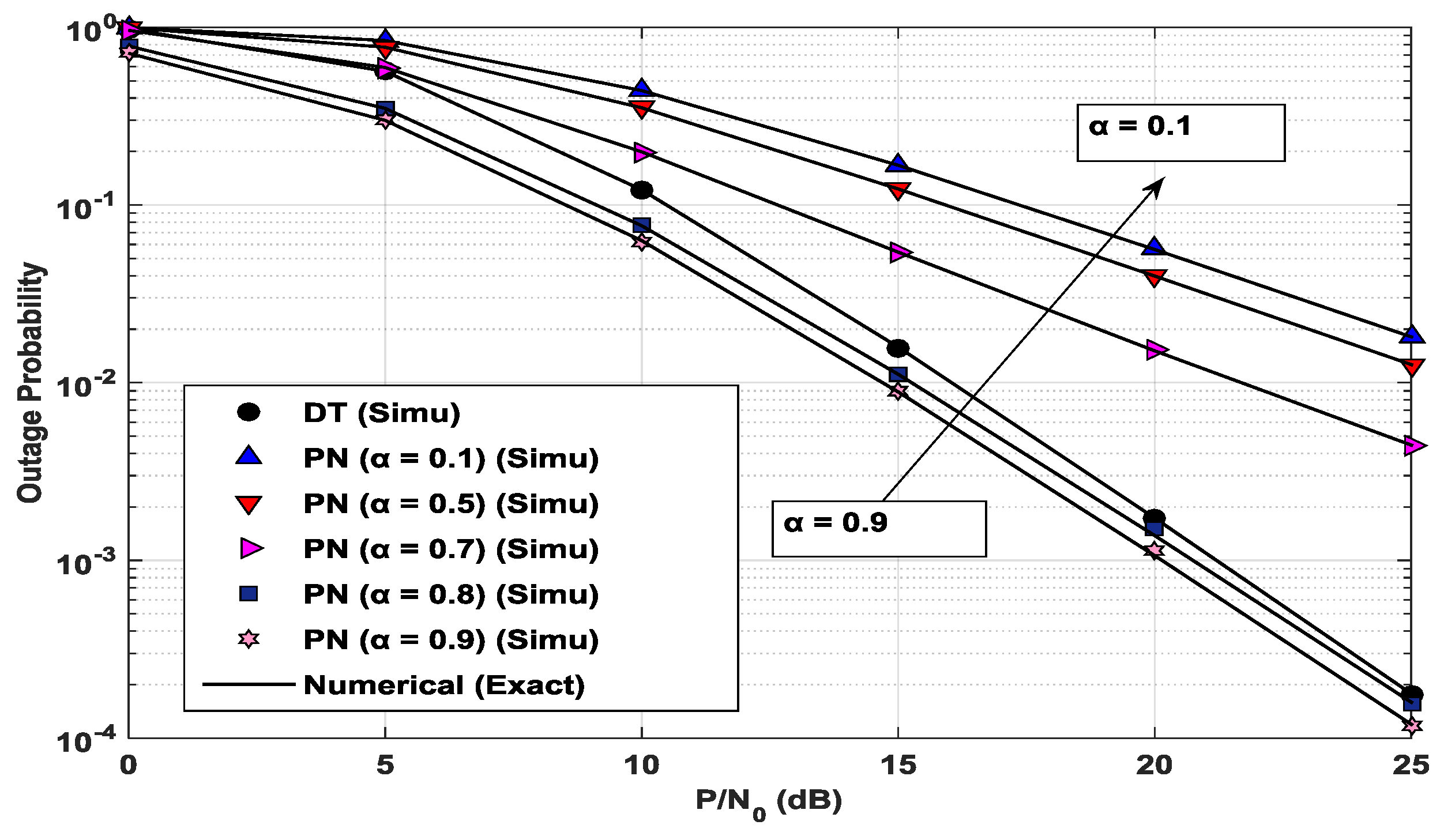
4.1. Validation of Numerical Results
4.2. Jointly Optimal Power Allocation for PN and Range of Power Sharing Coefficient for Minimum PN Performance
4.3. Impact of Other System Parameters on the Outage Probabilities of PN and SN
5. Conclusions
Author Contributions
Conflicts of Interest
Appendix A. Proof of Lemma 1
Appendix B. Proof of Theorem 1
References
- Akin, S.; Gursoy, M.C. Performance Analysis of Cognitive Radio Systems with Imperfect Channel Sensing and Estimation. IEEE Trans. Commun. 2015, 63, 1554–1566. [Google Scholar] [CrossRef]
- Hong, E.; Kim, K.; Har, D. Spectrum sensing by parallel pairs of cross-correlators and comb filters for OFDM systems with pilot tones. IEEE Sens. J. 2012, 12, 2380–2383. [Google Scholar] [CrossRef]
- Mahmoodi, S.E.; Subbalakshmi, K.P. A time-adaptive heuristic for cognitive cloud offloading in multi-RAT enabled wireless devices. IEEE Trans. Cogn. Commun. Netw. 2016, 2, 194–207. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, C.; Wang, J.; Dou, Z. A Novel Dynamic Spectrum Access Framework Based on Reinforcement Learning for Cognitive Radio Sensor Networks. Sensors 2016, 16, 1675. [Google Scholar] [CrossRef] [PubMed]
- Jing, G.; Durrani, S.; Zhao, X. Performance Analysis of Arbitrarily-Shaped Underlay Cognitive Networks: Effects of Secondary User Activity Protocols. IEEE Trans. Commun. 2015, 63, 376–389. [Google Scholar]
- Berbra, K.; Barkat, M.; Gini, F.; Greco, M.; Stinco, P. A Fast Spectrum Sensing for CP-OFDM Cognitive Radio Based on Adaptive Thresholding. Signal Process. 2016, 128, 252–261. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, T.; Sheng, M.; Zhu, Y. QoS-aware admission control and resource allocation in underlay device-to-device spectrum-sharing networks. IEEE J. Sel. Areas Commun. 2016, 34, 2874–2886. [Google Scholar] [CrossRef]
- Duy, T.T.; Kong, H.Y. Performance Analysis of Two-Way Hybrid Decode-and-Amplify Relaying Scheme with Relay Selection for Secondary Spectrum Access. Wirel. Pers. Commun. 2013, 69, 857–878. [Google Scholar] [CrossRef]
- Bornhorst, N.; Pesavento, M. Filter-and-forward Beamforming with Adaptive Decoding Delays in Asynchronous Multi-user Relay Networks. Signal Process. 2015, 109, 132–147. [Google Scholar] [CrossRef]
- Shalmashi, S.; Slimane, S.B. Performance Analysis of Relay-Assisted Cognitive Radio Systems with Superposition Coding. In Proceedings of the 2012 IEEE 23rd International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC 2012), Sydney, Australia, 9–12 September 2012; pp. 1226–1231.
- Hoan, T.; Hiep, V.; Koo, I. Multichannel-sensing scheduling and transmission-energy optimizing in cognitive radio networks with energy harvesting. Sensors 2016, 16, 461–478. [Google Scholar] [CrossRef] [PubMed]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kennedy, R.A. Relaying Protocols for Wireless Energy Harvesting and Information Processing. IEEE Trans. Wirel. Commun. 2013, 12, 3622–3636. [Google Scholar] [CrossRef]
- Esteves, V.; Antonopolous, A.; Kartsakli, E.; Puig-Vidal, M.; Miribel-Catala, P.; Verikoukis, C. Cooperative energy harvesting-adaptive MAC protocol for WBANs. Sensors 2015, 15, 12635–12650. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhong, C.; Suraweera, H.A.; Zheng, G.; Krikidis, I.; Zhang, Z. Wireless Information and Power Transfer With Full Duplex Relaying. IEEE Trans. Commun. 2014, 62, 3447–3461. [Google Scholar] [CrossRef]
- Usman, M.; Koo, I. Access Strategy for Hybrid Underlay-Overlay Cognitive Radios with Energy Harvesting. IEEE Sens. J. 2014, 14, 3164–3173. [Google Scholar] [CrossRef]
- Lee, S.; Zhang, R.; Huang, K. Opportunistic Wireless Energy Harvesting in Cognitive Radio Networks. IEEE Trans. Wirel. Commun. 2013, 12, 4788–4799. [Google Scholar] [CrossRef]
- Zhang, Q.; Cao, B.; Wang, Y.; Zhang, N.; Lin, X.; Sun, L. On exploiting polarization for energy-harvesting enabled cooperative cognitive radio networking. IEEE Wirel. Commun. 2013, 20, 116–124. [Google Scholar] [CrossRef]
- Gan, Z.; Ho, Z.; Jorswieck, E.A.; Ottersten, B. Information and Energy Cooperation in Cognitive Radio Networks. IEEE Trans. Signal Process. 2014, 62, 2290–2303. [Google Scholar]
- Zhang, F.; Jing, T.; Huo, Y.; Jiang, K. Outage Probability Minimization for Energy Harvesting Cognitive Radio Sensor Networks. Sensors 2017, 17, 224. [Google Scholar] [CrossRef] [PubMed]
- Ibarra, E.; Antonopoulos, A.; Kartsakli, E.; Rodrigues, J.J.P.C.; Verikoukis, C. QoS-Aware Energy Management in Body Sensor Nodes Powered by Human Energy Harvesting. IEEE Sens. J. 2016, 16, 542–549. [Google Scholar] [CrossRef]
- Ibarra, E.; Antonopoulos, A.; Kartsakli, E.; Verikoukis, C. HEH-BMAC: Hybrid Polling MAC Protocol for Wireless Body Area Networks Operated by Human Energy Harvesting. Telecommun. Syst. 2015, 58, 111–124. [Google Scholar] [CrossRef] [Green Version]
- Mekikis, P.V.; Antonopoulos, A.; Kartsakli, E.; Lalos, A.S.; Alonso, L.; Verikoukis, C. Information Exchange in Randomly Deployed Dense WSNs with Wireless Energy Harvesting Capabilities. IEEE Trans. Wirel. Commun. 2016, 15, 3008–3018. [Google Scholar] [CrossRef]
- Mekikis, P.V.; Lalos, A.S.; Antonopoulos, A.; Alonso, L.; Verikoukis, C. Wireless Energy Harvesting in Two-Way Network Coded Cooperative Communications: A Stochastic Approach for Large Scale Networks. IEEE Commun. Lett. 2014, 18, 1011–1014. [Google Scholar] [CrossRef]
- Mekikis, P.V.; Antonopoulos, A.; Kartsakli, E.; Alonso, L.; Verikoukis, C. Connectivity Analysis in Wireless-Powered Sensor Networks with Battery-Less Devices. In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM 2016), Washington, DC, USA, 4–8 December 2016; pp. 1–6.
- Guo, J.; Zhao, N.; Yu, F.R.; Liu, X.; Leung, V.C.M. Exploiting Adversarial Jamming Signals for Energy Harvesting in Interference Networks. IEEE Trans. Wirel. Commun. 2017, 16, 1267–1280. [Google Scholar] [CrossRef]
- Shin, K.; Park, I.; Hong, J.; Har, D.; Cho, D.H. Per-node throughput enhancement in Wi-Fi densenets. IEEE Commun. Mag. 2015, 53, 118–125. [Google Scholar] [CrossRef]
- Hamza, D.; Park, K.; Alouini, M.; Aissa, S. Throughput Maximization for Cognitive Radio Networks Using Active Cooperation and Superposition Coding. IEEE Trans. Wirel. Commun. 2015, 14, 3322–3336. [Google Scholar] [CrossRef]
- Huang, X.; Ansari, N. Optimal Cooperative Power Allocation for Energy-Harvesting-Enabled Relay Networks. IEEE Trans. Veh. Technol. 2016, 65, 2424–2434. [Google Scholar] [CrossRef]
- Baidas, M.W.; Alsusa, E.A. Power allocation, relay selection and energy cooperation strategies in energy harvesting cooperative wireless networks. Wirel. Commun. Mob. Comput. 2016, 16, 2065–2082. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, W.; Li, K. Power allocation and relay selection for energy efficient cooperation in wireless sensor networks with energy harvesting. EURASIP J. Wirel. Commun. Netw. 2017, 26, 1–11. [Google Scholar] [CrossRef]
- Neelamegam, D.; Rajesh, V. Development and analysis of microstrip antenna for Wireless Local Area Network (IEEE 802.11y). In Proceedings of the 2014 International Conference on Information Communication and Embedded Systems (ICICES 2014), Chennai, Tamil Nadu, India, 27–28 February 2014; pp. 1–5.
- Aust, S.; Ito, T. Sub 1GHz wireless LAN deployment scenarios and design implications in rural areas. In Proceedings of the 2011 IEEE GLOBECOM Workshops (GC Wkshps), Houston, TX, USA, 5–9 December 2011; pp. 1045–1049.
- Zhou, X.; Zhang, R.; Ho, C.K. Wireless Information and Power Transfer: Architecture Design and Rate-Energy Tradeoff. IEEE Trans. Commun. 2013, 61, 4754–4767. [Google Scholar] [CrossRef]
- Liu, P.; Tao, Z.; Lin, Z.; Erkip, E.; Panwar, S. Cooperative wireless communications: A cross-layer approach. IEEE Wirel. Commun. 2006, 13, 84–92. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M.; Jeffrey, A.; Zwillinger, D. Table of Integral, Series and Products, 7th ed.; Elsevier: Burlington, MA, USA, 2007. [Google Scholar]
- Chong, E.K.P.; Zak, S.H. An Introduction to Optimization, 4th ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]






| Parameter | Value |
|---|---|
| Power splitting ratio ρ | 0 < ρ < 1 |
| Power sharing coefficient α | 0 < α < 1 |
| Target rate RT | 1 (bits/s/Hz) |
| Target rate Rs | 0.5 (bits/s/Hz) |
| Path-loss exponent β | 3 |
| Energy conversion efficiency η | 0.9 |
| Fractional constant Ψ for power provided by battery | 0.1 |
| Noise variance parameter µ | 1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Son, P.N.; Har, D.; Cho, N.I.; Kong, H.Y. Optimal Power Allocation of Relay Sensor Node Capable of Energy Harvesting in Cooperative Cognitive Radio Network. Sensors 2017, 17, 648. https://doi.org/10.3390/s17030648
Son PN, Har D, Cho NI, Kong HY. Optimal Power Allocation of Relay Sensor Node Capable of Energy Harvesting in Cooperative Cognitive Radio Network. Sensors. 2017; 17(3):648. https://doi.org/10.3390/s17030648
Chicago/Turabian StyleSon, Pham Ngoc, Dongsoo Har, Nam Ik Cho, and Hyung Yun Kong. 2017. "Optimal Power Allocation of Relay Sensor Node Capable of Energy Harvesting in Cooperative Cognitive Radio Network" Sensors 17, no. 3: 648. https://doi.org/10.3390/s17030648
APA StyleSon, P. N., Har, D., Cho, N. I., & Kong, H. Y. (2017). Optimal Power Allocation of Relay Sensor Node Capable of Energy Harvesting in Cooperative Cognitive Radio Network. Sensors, 17(3), 648. https://doi.org/10.3390/s17030648






