The Impact of Estimating High-Resolution Tropospheric Gradients on Multi-GNSS Precise Positioning
Abstract
:1. Introduction
2. Multi-GNSS Ionosphere-Free PPP Observation Model
3. Experimental Data and Processing Strategy
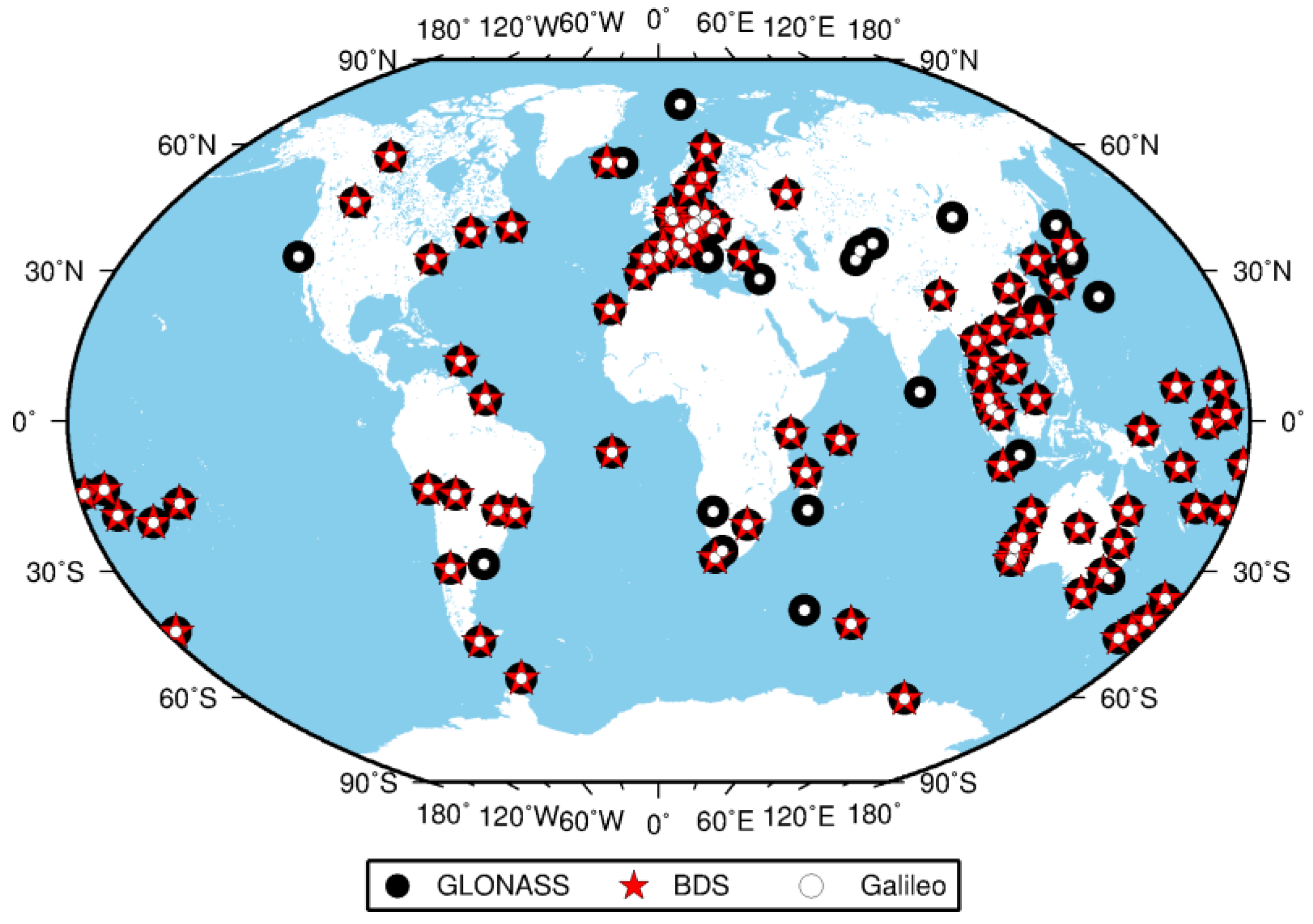
3.1. Dataset
3.2. Processing Strategy
4. Results and Analysis
4.1. Temporal Resolution Dependence
4.2. Elevation Cutoff Angle Dependence
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Davis, J.L.; Elgered, G.; Niell, A.E.; Kuehn, C.E. Ground-based measurement of gradients in the “wet” radio refractivity of air. Radio Sci. 1993, 28, 1003–1018. [Google Scholar] [CrossRef]
- MacMillan, D.S. Atmospheric gradients from very long baseline interferometry observations. Geophys. Res. Lett. 1995, 22, 1041–1044. [Google Scholar] [CrossRef]
- Chen, G.; Herring, T.A. Effects of atmospheric azimuthal asymmetry on the analysis of space geodetic data. J. Geophys. Res. 1997, 102, 20489–20502. [Google Scholar] [CrossRef]
- Bar-Sever, Y.E.; Kroger, P.M.; Borjesson, J.A. Estimating horizontal gradients of tropospheric path delay with a single GPS receiver. J. Geophys. Res. 1998, 103, 5019–5035. [Google Scholar] [CrossRef]
- Willis, P.; Bar-Sever, Y.E.; Bock, O. Estimating horizontal tropospheric gradients in DORIS data processing: Preliminary results. Geod. Planet Earth 2012, 136, 1013–1019. [Google Scholar]
- Boehm, J.; Schuh, H. Troposphere gradients from the ECMWF in VLBI analysis. J. Geod. 2007, 81, 403–408. [Google Scholar] [CrossRef]
- Iwabuchi, T.; Miyazaki, S.; Heki, K.; Naito, I.; Hatanaka, Y. An impact of estimating tropospheric delay gradients on tropospheric delay estimations in the summer using the Japanese nationwide GPS array. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Herring, T.A. Modelling atmospheric delays in the analysis of space geodetic data. In Symposium on Refraction of Transatmospheric Signals in Geodesy; DeMunk, J.C., Spoelstra, T.A., Eds.; Netherlands Geodetic Commission: Delft, The Netherlands, 1992; Volume 36, pp. 157–164. [Google Scholar]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Miyazaki, S.; Iwabuchi, T.; Heki, K.; Naito, I. An impact of estimating tropospheric delay gradients on precise positioning in the summer using the Japanese nationwide GPS array. J. Geophys. Res. 2003, 108, 2335–2345. [Google Scholar] [CrossRef]
- Meindl, M.; Schaer, S.; Hugentobler, U.; Beutler, G. Tropospheric gradient estimation at CODE: Results from global solutions. J. Meteorol. Soc. Jpn. 2004, 82, 331–338. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P.; Hugentobler, U.; Teunissen, P.; Nakamura, S. Initial assessment of the COMPASS/BeiDou-2 regional navigation satellite system. GPS Solut. 2013, 17, 211–222. [Google Scholar] [CrossRef]
- Shi, C.; Zhao, Q.; Hu, Z.; Liu, J. Precise relative positioning using real tracking data from COMPASS GEO and IGSO satellites. GPS Solut. 2013, 17, 103–119. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Wang, A.; Xu, J.; He, H.; Guo, H.; Shen, J.; Dai, X. Preliminary assessment of the navigation and positioning performance of BeiDou regional navigation satellite system. Sci. China Earth Sci. 2014, 57, 144–152. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Precise positioning with current multi-constellation Global Navigation Satellite Systems: GPS, GLONASS, Galileo and BeiDou. Sci. Rep. 2015, 5, 8328–8341. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Yuan, Y.; Zhang, B.; Wang, N.; Tan, B.; Chen, Y. Multi-GNSS precise point positioning (MGPPP) using raw observations. J. Geod. 2017, 91, 253–268. [Google Scholar] [CrossRef]
- Cai, C.; Gao, Y.; Pan, L.; Zhu, J. Precise point positioning with quad-constellations: GPS, BeiDou, GLONASS and Galileo. Adv. Space Res. 2015, 56, 133–143. [Google Scholar] [CrossRef]
- Li, X.; Zus, F.; Lu, C.; Dick, G.; Ning, T.; Ge, M.; Wickert, J.; Schuh, H. Retrieving of atmospheric parameters from multi-GNSS in real time: Validation with water vapor radiometer and numerical weather model. J. Geophys. Res. Atmos. 2015, 120, 7189–7204. [Google Scholar] [CrossRef]
- Lu, C.; Li, X.; Li, Z.; Heinkelmann, R.; Nilsson, T.; Dick, G.; Ge, M.; Schuh, H. GNSS tropospheric gradients with high temporal resolution and their effect on precise positioning. J. Geophys. Res. Atmos. 2016, 121, 912–930. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Sturze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)—Achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction Part II. Refraction corrections in satellite geodesy. Bull. Geoid. 1973, 47, 13–34. [Google Scholar] [CrossRef]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global mapping function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, L07304. [Google Scholar] [CrossRef]
- Rizos, C.; Montenbruck, O.; Weber, R.; Neilan, R.; Hugentobler, U. The IGS MGEX Experiment as a milestone for a comprehensive multi-GNSS service. In Proceedings of the ION-PNT-2013, Honolulu, HI, USA, 22–25 April 2013. [Google Scholar]
- Montenbruck, O.; Steigenberger, P.; Khachikyan, R.; Weber, G.; Langley, R.B.; Mervart, L.; Hugentobler, U. IGS-MGEX: Preparing the ground for multi-constellation GNSS science. Inside GNSS 2014, 9, 42–49. [Google Scholar]
- Liu, J.; Ge, M. PANDA software and its preliminary result of positioning and orbit determination. Wuhan Univ. J. Nat. Sci. 2003, 8, 603–609. [Google Scholar]
- Deng, Z.; Fritsche, M.; Uhlemann, M.; Wickert, J.; Schuh, H. Reprocessing of GFZ Multi-GNSS product GBM. Proceedings of IGS Workshop, Sydney, Australia, 8–12 February 2016. [Google Scholar]
- Dilssner, F.; Springer, T.; Schoenemann, E.; Enderle, W. Estimation of satellite antenna phase center corrections for BeiDou. In Proceedings of the IGS workshop, Pasadena, CA, USA, 23–27 June 2014. [Google Scholar]
- Gendt, G.; Dick, G.; Reigber, C.; Tomassini, M.; Liu, Y.; Ramatschi, M. Near real time GPS water vapor monitoring for numerical weather prediction in Germany. J. Meteorol. Soc. Jpn. 2004, 82, 361–370. [Google Scholar] [CrossRef]
- Wu, J.; Wu, S.; Hajj, G.; Bertiger, W.; Lichten, S. Effects of antenna orientation on GPS carrier phase. Manuscr. Geod. 1993, 18, 91–98. [Google Scholar]
- Boehm, J.; Heinkelmann, R.; Schuh, H. Short note: A global model of pressure and temperature for geodetic applications. J. Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- McCarthy, D.; Petit, G. IERS Conventions; Federal Agency for Cartography and Geodesy: Frankfurt, Germany, 2010. [Google Scholar]
- Leick, A.; Papoport, L.; Tatarnikov, D. GPS Satellite Surveying, 4th ed.; John Wiley and Sons: New York, NY, USA, 2015. [Google Scholar]
- Xu, G. GPS: Theory, Algorithm and Applications, 2nd ed.; Springer Verlag: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Schmid, R.; Dach, R.; Collilieux, X.; Jäggi, A.; Schmitz, M.; Dilssner, F. Absolute IGS antenna phase center model igs08.atx: Status and potential improvements. J. Geod. 2015, 90, 343–364. [Google Scholar] [CrossRef]





| Items | Descriptions |
|---|---|
| Number of stations | 134 |
| Number of satellites | GPS: 32; GLONASS: 24; BDS: 14; Galileo: 10 |
| Procedure | Integrated processing, all the observations from different GNSSs in one common parameter adjustment procedure |
| Estimator | Least squares (LSQ) estimator in batch mode |
| Observables | Undifferenced ionosphere-free combined observables from raw code and phase observations |
| Signal selection | GPS: L1/L2; GLONASS: L1/L2; BDS: B1/B2; Galileo: E1/E5a |
| Sampling rate | 30 s |
| Elevation cutoff | 3°/5°/7°/10°/12°/15°/20° |
| Observation weighting | A priori precision 0.6 m and 0.01 cycle for raw code and phase observations, respectively Elevation-dependent, 1 for , otherwise [28] |
| Phase wind-up | Corrected [29] |
| Tropospheric delay | ZHD: corrected with global pressure and temperature (GPT) [30] model using the formulas of Saastamoinen [21] ZWD: estimated as a continuous piece-wise linear function (2 h parameter spacing), GMF [22] mapping function |
| Tropospheric gradients | Estimated as a continuous piece-wise linear function with different temporal resolutions |
| Tidal displacements | Solid Earth tide, pole tide, ocean tide loading corrections according to IERS Conventions 2010 [31] |
| Relativistic effect | Applied [32] |
| Sagnac effect | Applied [33] |
| Satellite antenna PCOs and PCVs | GPS and GLONASS: fixed to the values from igs08.atx [34]; BDS: fixed to nominal values (0.6, 0.0, 1.1 m) for GEO, and fixed to the estimated values provided by Dilssner et al. [27] for IGSO and MEO; Galileo: fixed to nominal values (0.2, 0.0, 0.6 m) |
| Receiver antenna PCOs and PCVs | PCO and PCV corrections for GPS and GLONASS are from igs08.atx; Corrections for BDS and Galileo are assumed the same with GPS |
| Receiver clock | Estimated as white noise |
| ISBs/IFBs | Estimated as daily constants without a priori constraints |
| Station coordinates | Estimated as static |
| Phase ambiguities | Estimated, constant for each continuous arc; float value |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, F.; Li, X.; Li, W.; Chen, W.; Dong, D.; Wickert, J.; Schuh, H. The Impact of Estimating High-Resolution Tropospheric Gradients on Multi-GNSS Precise Positioning. Sensors 2017, 17, 756. https://doi.org/10.3390/s17040756
Zhou F, Li X, Li W, Chen W, Dong D, Wickert J, Schuh H. The Impact of Estimating High-Resolution Tropospheric Gradients on Multi-GNSS Precise Positioning. Sensors. 2017; 17(4):756. https://doi.org/10.3390/s17040756
Chicago/Turabian StyleZhou, Feng, Xingxing Li, Weiwei Li, Wen Chen, Danan Dong, Jens Wickert, and Harald Schuh. 2017. "The Impact of Estimating High-Resolution Tropospheric Gradients on Multi-GNSS Precise Positioning" Sensors 17, no. 4: 756. https://doi.org/10.3390/s17040756
APA StyleZhou, F., Li, X., Li, W., Chen, W., Dong, D., Wickert, J., & Schuh, H. (2017). The Impact of Estimating High-Resolution Tropospheric Gradients on Multi-GNSS Precise Positioning. Sensors, 17(4), 756. https://doi.org/10.3390/s17040756





