A Review of Rock Bolt Monitoring Using Smart Sensors
Abstract
:1. Introduction
2. Basics and Types of Rock Bolts
- Mechanically anchored rock bolts;
- Friction-anchored rock bolts;
- Fully grouted rock bolts;
- Instrumented rock bolts.
2.1. Mechanically Anchored Rock Bolts
2.2. Friction Anchored Bolts
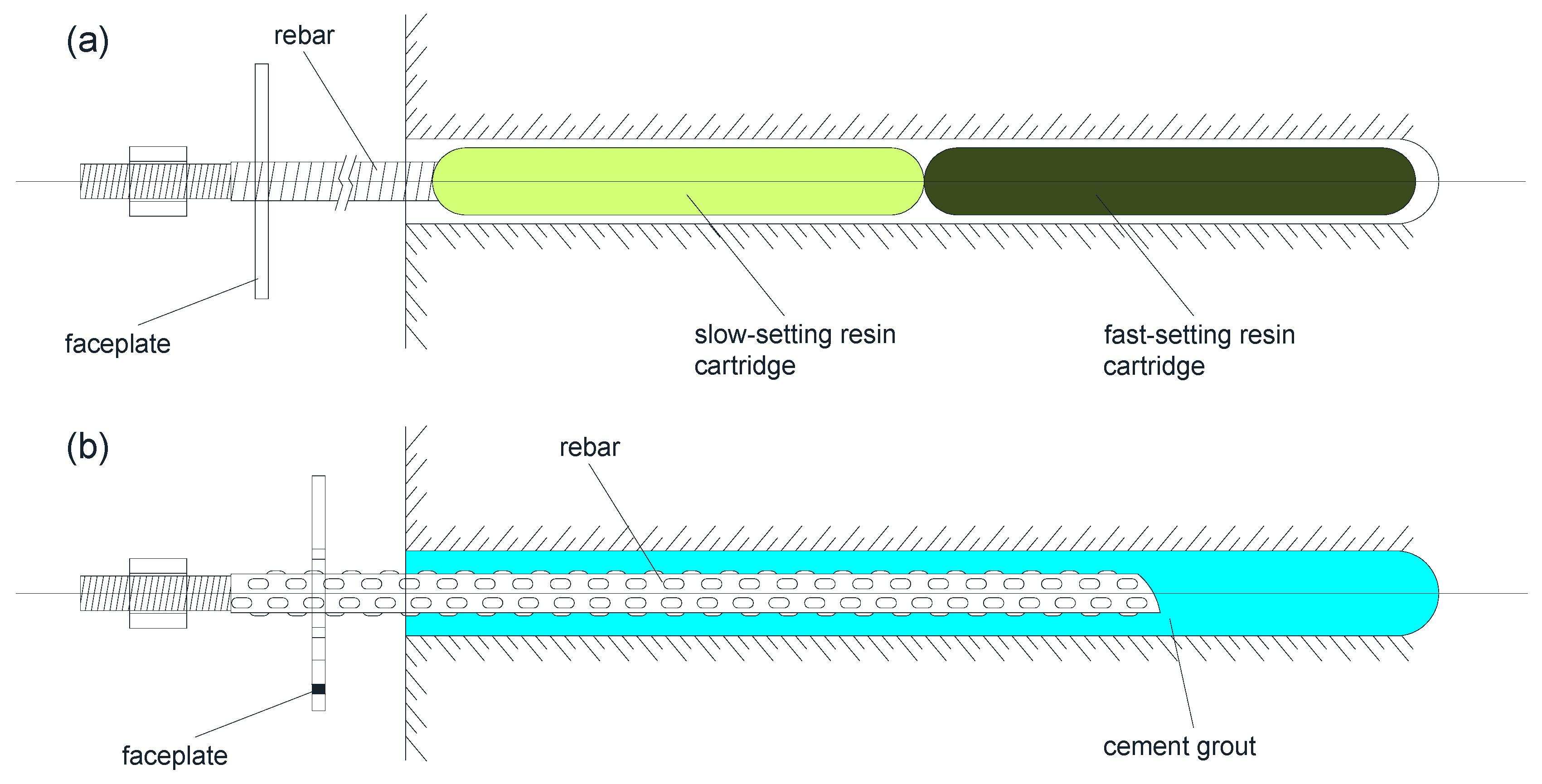
2.3. Fully Grouted Rock Bolts
2.4. Instrumented Rock Bolts
3. Related Smart Sensors
3.1. Piezoelectric Sensors
Guided Ultrasonic Waves in a Cylinder
3.2. Fiber Optic Sensors
3.2.1. FBG Sensors
3.2.2. BOTDR Distributed Sensors
4. Rock Bolt Monitoring Using Smart Sensors
4.1. Load Monitoring
4.1.1. Traditional Load Monitoring Methods
4.1.2. Load Monitoring Based on FBG Sensors
4.1.3. Load Monitoring Based on Distributed Brillouin Sensing
4.2. Corrosion Monitoring
4.3. Grout Quality Testing
4.4. Delamination Monitoring for Grouted Rock Bolts
4.5. Rock Bolt Devices with NDT Capability
5. Future Trends
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Benmokrane, B.; Chekired, M.; Xu, H. Monitoring behavior of grouted anchors using vibrating-wire gauges. J. Geotech. Eng. 1995, 121, 466–475. [Google Scholar] [CrossRef]
- Kılıc, A.; Yasar, E.; Atis, C. Effect of bar shape on the pull-out capacity of fully-grouted rockbolts. Tunn. Undergr. Space Technol. 2003, 18, 1–6. [Google Scholar] [CrossRef]
- Mark, C.; Pappas, D.; Barczak, T. Current trends in reducing ground fall accidents in US coal mines. Min. Eng. 2011, 63, 60–65. [Google Scholar]
- Maiti, J.; Khanzode, V.V. Development of a relative risk model for roof and side fall fatal accidents in underground coal mines in india. Saf. Sci. 2009, 47, 1068–1076. [Google Scholar] [CrossRef]
- Buys, B.J.; Heyns, P.S.; Loveday, P. Rock bolt condition monitoring using ultrasonic guided waves. J. South. Afr. Inst. Min. Metall. 2009, 109, 95–105. [Google Scholar]
- Duzgun, H.; Einstein, H. Assessment and management of roof fall risks in underground coal mines. Saf. Sci. 2004, 42, 23–41. [Google Scholar] [CrossRef]
- Crosky, A.; Smith, B.; Hebblewhite, B. Failure of rockbolts in underground mines in australia. Pract. Fail. Anal. 2003, 3, 70–78. [Google Scholar] [CrossRef]
- Kelly, A.; Jager, A. Critically evaluate techniques for the in situ testing of steel tendon grouting effectiveness as a basis for reducing fall of ground injuries and fatalities. Safety in Mines Research Advisory Committee: Johannesburg, South Africa, 1996; pp. 1–108. [Google Scholar]
- Li, C.C. A new energy-absorbing bolt for rock support in high stress rock masses. Int. J. Rock Mech. Min. Sci. 2010, 47, 396–404. [Google Scholar]
- Kılıc, A.; Yasar, E.; Celik, A. Effect of grout properties on the pull-out load capacity of fully grouted rock bolt. Tunn. Undergr. Space Technol. 2002, 17, 355–362. [Google Scholar] [CrossRef]
- Canbulat, I. Evaluation and Design of Optimum Support Systems in South African Collieries Using the Probabilistic Design Approach. Ph.D. Thesis, University of Pretoria, Pretoria, South Africa, 2008. [Google Scholar]
- Hoek, E.; Kaiser, P.K.; Bawden, W.F. Support of Underground Excavations in Hard Rock; A.A.Balkema: Rotterdam, The Netherlands, 1995. [Google Scholar]
- Li, C. Design principles of rock support for underground excavations. In Proceedings of the ISRM International Symposium-EUROCK 2012, Stockholm, Sweden, 28–30 May 2012. [Google Scholar]
- Luo, J. A New Rock Bolt Design Criterion and Knowlwdge-Based Expert System for Stratified Roof. Ph.D. Thesis, Virginia Tech, Blackshurg, VA, USA, 1 July 1999. [Google Scholar]
- Li, C.C. Performance of d-bolts under static loading. Rock Mech. Rock Eng. 2012, 45, 183–192. [Google Scholar] [CrossRef]
- Peng, S.S.; Tang, D. Roof bolting in underground mining: A state-of-the-art review. Int. J. Min. Eng. 1984, 2, 1–42. [Google Scholar] [CrossRef]
- Kendorski, F.S. Rock reinforcement longevity. Geo-Strata—Geo Inst. ASCE 2003, 4, 9–12. [Google Scholar]
- Tressler, J.F.; Alkoy, S.; Newnham, R.E. Piezoelectric sensors and sensor materials. J. Electroceram. 1998, 2, 257–272. [Google Scholar] [CrossRef]
- Duan, W.H.; Wang, Q.; Quek, S.T. Applications of piezoelectric materials in structural health monitoring and repair: Selected research examples. Materials 2010, 3, 5169–5194. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Structural Health Monitoring: With Piezoelectric Wafer Active Sensors; Academic Press: New York, NY, USA, 2007. [Google Scholar]
- Lin, X.; Yuan, F. Diagnostic lamb waves in an integrated piezoelectric sensor/actuator plate: Analytical and experimental studies. Smart Mater. Struct. 2001, 10, 907. [Google Scholar] [CrossRef]
- Kessler, S.S.; Spearing, S.M.; Soutis, C. Damage detection in composite materials using lamb wave methods. Smart Mater. Struct. 2002, 11, 269. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Tuned lamb wave excitation and detection with piezoelectric wafer active sensors for structural health monitoring. J. Intell. Mater. Syst. Struct. 2005, 16, 291–305. [Google Scholar] [CrossRef]
- Liang, Y.; Li, D.; Parvasi, S.M.; Kong, Q.; Song, G. Bond-slip detection of concrete-encased composite structure using electro-mechanical impedance technique. Smart Mater. Struct. 2016, 25, 095003. [Google Scholar] [CrossRef]
- Dugnani, R.; Zhuang, Y.; Kopsaftopoulos, F.; Chang, F.-K. Adhesive bond-line degradation detection via a cross-correlation electromechanical impedance–based approach. Struct. Health Monit. 2016, 6, 650–667. [Google Scholar] [CrossRef]
- Park, S.; Lee, J.-J.; Yun, C.-B.; Inman, D.J. Electro-mechanical impedance-based wireless structural health monitoring using pca-data compression and k-means clustering algorithms. J. Intell. Mater. Syst. Struct. 2008, 19, 509–520. [Google Scholar] [CrossRef]
- Chan, H.; Masserey, B.; Fromme, P. High frequency guided ultrasonic waves for hidden fatigue crack growth monitoring in multi-layer model aerospace structures. Smart Mater. Struct. 2015, 24, 025037. [Google Scholar] [CrossRef]
- Li, W.; Kong, Q.; Ho, S.C.M.; Mo, Y.; Song, G. Feasibility study of using smart aggregates as embedded acoustic emission sensors for health monitoring of concrete structures. Smart Mater. Struct. 2016, 25, 115031. [Google Scholar] [CrossRef]
- Perelli, A.; De Marchi, L.; Marzani, A.; Speciale, N. Acoustic emission localization in plates with dispersion and reverberations using sparse pzt sensors in passive mode. Smart Mater. Struct. 2012, 21, 025010. [Google Scholar] [CrossRef]
- Beard, M.; Lowe, M. Non-destructive testing of rock bolts using guided ultrasonic waves. Int. J. Rock Mech. Min. Sci. 2003, 40, 527–536. [Google Scholar] [CrossRef]
- Beard, M.; Lowe, M.; Cawley, P. Ultrasonic guided waves for inspection of grouted tendons and bolts. J. Mater. Civil Eng. 2003, 15, 212–218. [Google Scholar] [CrossRef]
- Li, H.-N.; Li, D.-S.; Song, G.-B. Recent applications of fiber optic sensors to health monitoring in civil engineering. Eng. Struct. 2004, 26, 1647–1657. [Google Scholar] [CrossRef]
- Meltz, G.; Morey, W.W.; Glenn, W. Formation of bragg gratings in optical fibers by a transverse holographic method. Opt. Lett. 1989, 14, 823–825. [Google Scholar] [CrossRef] [PubMed]
- Lau, K.-T.; Yuan, L.; Zhou, L.-M.; Wu, J.; Woo, C.-H. Strain monitoring in frp laminates and concrete beams using fbg sensors. Compos. Struct. 2001, 51, 9–20. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, B.; Hayashi, K.; Machida, A. Distributed optic fiber sensing for a full-scale pc girder strengthened with prestressed pbo sheets. Eng. Struct. 2006, 28, 1049–1059. [Google Scholar] [CrossRef]
- Zhang, D.; Shi, B.; Cui, H.; Xu, H. Improvement of spatial resolution of brillouin optical time domain reflectometer using spectral decomposition. Opt. Appl. 2004, 34, 291–302. [Google Scholar]
- Barrias, A.; Casas, J.R.; Villalba, S. A review of distributed optical fiber sensors for civil engineering applications. Sensors 2016, 16, 748. [Google Scholar] [CrossRef] [PubMed]
- Mitri, H. Evaluation of rock support performance through instrumentation and monitoring of bolt axial load. In Proceedings of the 11th Underground Coal Operators’ Conference, Wollongong, Australia, 21–23 March 2011; pp. 136–140. [Google Scholar]
- Mitri, H.; Marwan, J. A new rockbolt axial load measuring device. In Proceedings of the 20th International Conference on Ground Control in Mining, Morgantown, WV, USA, 7–9 August 2001; pp. 367–373. [Google Scholar]
- Mitri, H.; Laroche, L. New technology for ground monitoring in underground mines using instrumented rockbolts. In Proceedings of the Mine Planning and Equipment Selection Symposium, Wroclaw, Poland, 1–3 September 2004; pp. 469–478. [Google Scholar]
- Frank, A.; Nellen, P.M.; Broennimann, R.; Sennhauser, U.J. Fiber optic bragg grating sensors embedded in gfrp rockbolts. In Proceedings of the 1999 Symposium on Smart Structures and Materials, Newport Beach, CA, USA, 1–4 March 1999; pp. 497–504. [Google Scholar]
- Nellen, P.M.; Broennimann, R.; Frank, A.; Mauron, P.; Sennhauser, U.J. Structurally embedded fiber bragg gratings: Civil engineering applications. In Proceedings of the Photonics East’99, International Society for Optics and Photonics, Boston, MA, USA, 19 September 1999; pp. 44–54. [Google Scholar]
- Nellen, P.M.; Frank, A.; Broennimann, R.; Sennhauser, U.J. Optical fiber bragg gratings for tunnel surveillance. In Proceedings of the SPIE’s 7th Annual International Symposium on Smart Structures and Materials, Newport, DE, USA, 1–5 March 2000; pp. 263–270. [Google Scholar]
- Schroeck, M.; Ecke, W.; Graupner, A. Strain monitoring in steel rock bolts using fbg sensor arrays. Proc. SPIE 2000, 4074. [Google Scholar] [CrossRef]
- Moerman, W.; Taerwe, L.; De Waele, W.; Degrieck, J.; Himpe, J. Measuring ground anchor forces of a quay wall with bragg sensors. J. Struct. Eng. 2005, 131, 322–328. [Google Scholar] [CrossRef]
- Ho, S.C.M.; Li, W.; Wang, B.; Song, G. A Load Measuring Anchor Plate for Rock Bolt Using Fiber Optic Sensor. Smart Mater. Struct. 2017. under review. [Google Scholar]
- Weng, X.; Ma, H.; Wang, J. Stress monitoring for anchor rods system in subway tunnel using fbg technology. Adv. Mater. Sci. Eng. 2015, 2015. [Google Scholar] [CrossRef]
- Do, T.M.; Kim, Y.-S. Prediction of load transfer depth for cost-effective design of ground anchors using fbg sensors embedded tendon and numerical analysis. Geomech. Eng. 2016, 10, 737–755. [Google Scholar] [CrossRef]
- Iten, M.; Puzrin, A.M. Monitoring of stress distribution along a ground anchor using botda. Proc. SPIE 2010, 7647. [Google Scholar] [CrossRef]
- Moffat, R.A.; Beltran, J.F.; Herrera, R. Applications of botdr fiber optics to the monitoring of underground structures. Geomech. Eng. 2015, 9, 397–414. [Google Scholar] [CrossRef]
- Spearing, A.; Mondal, K.; Bylapudi, G.; Hirschi, J. The corrosion of rock anchors in US coal mines. In Proceedings of the SME Annual Meeting, Phoenix, AZ, USA, 28 February–3 March 2010. [Google Scholar]
- Aziz, N.; Craig, P.; Nemcik, J.; Hai, F. Rock bolt corrosion—An experimental study. Min. Technol. 2014, 123, 69–77. [Google Scholar] [CrossRef]
- Craig, P.; Serkan, S.; Hagan, P.; Hebblewhite, B.; Vandermaat, D.; Crosky, A.; Elias, E. Investigations into the corrosive environments contributing to premature failure of australian coal mine rock bolts. Int. J. Min. Sci. Technol. 2016, 26, 59–64. [Google Scholar] [CrossRef]
- Vandermaat, D.; Saydam, S.; Hagan, P.; Crosky, A. Examination of rockbolt stress corrosion cracking utilising full size rockbolts in a controlled mine environment. Int. J. Rock Mech. Min. Sci. 2016, 81, 86–95. [Google Scholar] [CrossRef]
- Spearing, A.; Mondal, K.; Bylapudi, G.; Hirschi, J.C. A method to determine the corrosion potential of rock bolts on coal mines. In Proceedings of the 29th International Conference on Ground Contorl in Mining, Morgantown, WV, USA, 27–29 July 2010. [Google Scholar]
- Wei, H.; Zhao, X.; Li, D.; Zhang, P.; Sun, C. Corrosion monitoring of rock bolt by using a low coherent fiber-optic interferometry. Opt. Laser Technol. 2015, 67, 137–142. [Google Scholar] [CrossRef]
- Zou, D.S. Analysis of in situ rock bolt loading status. Int. J. Rock Mech. Min. Sci. 2004, 41, 762–767. [Google Scholar] [CrossRef]
- Madenga, V.; Zou, D.; Zhang, C. Effects of curing time and frequency on ultrasonic wave velocity in grouted rock bolts. J. Appl. Geophys. 2006, 59, 79–87. [Google Scholar] [CrossRef]
- Cui, Y.; Zou, D. Numerical simulation of attenuation and group velocity of guided ultrasonic wave in grouted rock bolts. J. Appl. Geophys. 2006, 59, 337–344. [Google Scholar] [CrossRef]
- Zou, D.S.; Cheng, J.; Yue, R.; Sun, X. Grout quality and its impact on guided ultrasonic waves in grouted rock bolts. J. Appl. Geophys. 2010, 72, 102–106. [Google Scholar] [CrossRef]
- Cui, Y.; Zou, D. Assessing the effects of insufficient rebar and missing grout in grouted rock bolts using guided ultrasonic waves. J. Appl. Geophys. 2012, 79, 64–70. [Google Scholar] [CrossRef]
- Zou, D.; Cui, Y.; Madenga, V.; Zhang, C. Effects of frequency and grouted length on the behavior of guided ultrasonic waves in rock bolts. Int. J. Rock Mech. Min. Sci. 2007, 44, 813–819. [Google Scholar] [CrossRef]
- Zou, D.; Cui, Y. A new approach for field instrumentation in grouted rock bolt monitoring using guided ultrasonic waves. J. Appl. Geophys. 2011, 75, 506–512. [Google Scholar] [CrossRef]
- Lee, J.; Kim, H.; Lee, I.; Han, S.; Lee, Y. Rock bolt integrity evaluation in tunnelling using ultrasonic ndt techniques. In Proceedings of the Proceedings of the World Tunnel Congress 2007 and 33rd ITA/AITES Annual General Assembly, Prague, Czech Republic, 5–10 May 2007; pp. 321–326. [Google Scholar]
- Han, S.-I.; Lee, I.-M.; Lee, Y.-J.; Lee, J.-S. Evaluation of rock bolt integrity using guided ultrasonic waves. Geotech. Test. J. 2009, 32, 31–38. [Google Scholar]
- Lee, I.-M.; Han, S.-I.; Kim, H.-J.; Yu, J.-D.; Min, B.-K.; Lee, J.-S. Evaluation of rock bolt integrity using fourier and wavelet transforms. Tunn. Undergr. Space Technol. 2012, 28, 304–314. [Google Scholar] [CrossRef]
- Yu, J.-D.; Bae, M.-H.; Lee, I.-M.; Lee, J.-S. Nongrouted ratio evaluation of rock bolts by reflection of guided ultrasonic waves. J. Geotech. Geoenviron. Eng. 2012, 139, 298–307. [Google Scholar] [CrossRef]
- He, C.; Van Velsor, J.; Lee, C.; Rose, J. Health monitoring of rock bolts using ultrasonic guided waves. In Proceedings of the AIP Conference Proceedings, Salt Lake City, UT, USA, 10–11 August 2005; p. 195. [Google Scholar]
- Zeng, L.; Parvasi, S.M.; Kong, Q.; Huo, L.; Li, M.; Song, G. Bond slip detection of concrete-encased composite structure using shear wave based active sensing approach. Smart Mater. Struct. 2015, 24, 125026. [Google Scholar] [CrossRef]
- Starkey, A.; Ivanovic, A.; Neilson, R.D.; Rodger, A.A. Using a lumped parameter dynamic model of a rock bolt to produce training data for a neural network for diagnosis of real data. Meccanica 2003, 38, 133–144. [Google Scholar] [CrossRef]
- Delsing, J.; Eliasson, J.; Pereira, P.P.; Gebart, J. The IoT rockbolt. In Proceedings of the 5th International Conference on Internet of Things, Seul, Korea, 26–28 October 2015. [Google Scholar]
- Puñal Pereira, P. Efficient IoT Framework for Industrial Applications. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2016. [Google Scholar]
- Stepinski, T.; Matsson, K.-J. Rock bolt inspection by means of rbt instrument. In Proceedings of the 19th World Conference on Non-Destructive Testing, Munich, Germany, 13–17 June 2016. [Google Scholar]
- Wang, B.; Huo, L.; Chen, D.; Li, W.; Song, G. Impedance-based pre-stress monitoring of rock bolts using a piezoceramic-based smart washer—A feasibility study. Sensors 2017, 17, 250. [Google Scholar] [CrossRef] [PubMed]
- Yin, H.; Wang, T.; Yang, D.; Liu, S.; Shao, J.; Li, Y. A smart washer for bolt looseness monitoring based on piezoelectric active sensing method. Appl. Sci. 2016, 6, 320. [Google Scholar] [CrossRef]
- Wang, T.; Song, G.; Wang, Z.; Li, Y. Proof-of-concept study of monitoring bolt connection status using a piezoelectric based active sensing method. Smart Mater. Struct. 2013, 22, 087001. [Google Scholar] [CrossRef]


























© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, G.; Li, W.; Wang, B.; Ho, S.C.M. A Review of Rock Bolt Monitoring Using Smart Sensors. Sensors 2017, 17, 776. https://doi.org/10.3390/s17040776
Song G, Li W, Wang B, Ho SCM. A Review of Rock Bolt Monitoring Using Smart Sensors. Sensors. 2017; 17(4):776. https://doi.org/10.3390/s17040776
Chicago/Turabian StyleSong, Gangbing, Weijie Li, Bo Wang, and Siu Chun Michael Ho. 2017. "A Review of Rock Bolt Monitoring Using Smart Sensors" Sensors 17, no. 4: 776. https://doi.org/10.3390/s17040776
APA StyleSong, G., Li, W., Wang, B., & Ho, S. C. M. (2017). A Review of Rock Bolt Monitoring Using Smart Sensors. Sensors, 17(4), 776. https://doi.org/10.3390/s17040776






