Node Scheduling Strategies for Achieving Full-View Area Coverage in Camera Sensor Networks
Abstract
:1. Introduction
- We deduce the necessary and sufficient conditions of the FACM problem for the local point and study the geometric parameters, the maximum full-view neighborhood coverage and the position trajectory of sensors around the local point.
- We find that the full-view area coverage can be guaranteed approximately, as long as the regular hexagons decided by the virtual grids are seamlessly stitched.
- We propose two solutions for camera sensors for two different deployment strategies, respectively. By computing the theoretical optimal length of the virtual grids, the deployment pattern algorithm (DPA) for FACM is presented in the deterministic implementation. For reducing the redundancy in random deployment, a local neighboring-optimal selection algorithm (LNSA) is devised for achieving the full-view coverage in the grid points.
2. Related Work
3. Problem Description and Assumptions
3.1. Network Model
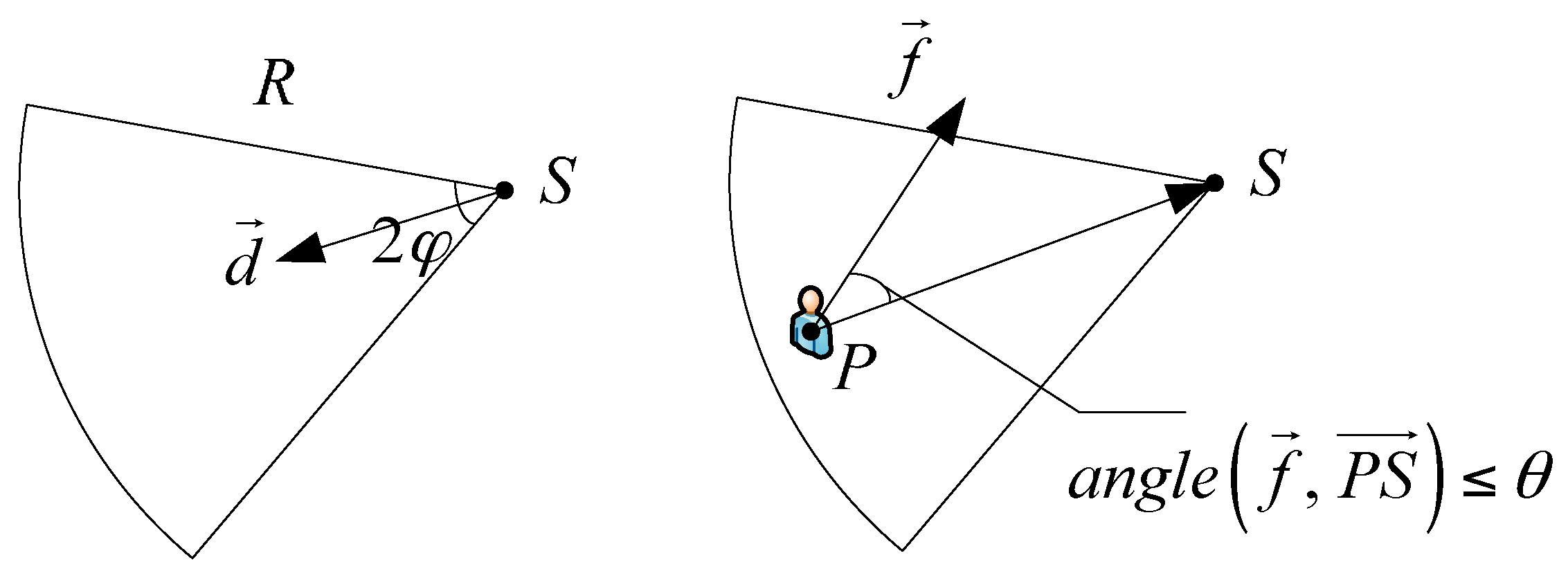
- The one condition is that the intruder location P must fall within the field of view sensed by the camera node, which is donated by .
- The one other condition is that the angle between the object’s facing direction and the camera’s working direction is less than or equal to the effective angle, i.e., .
3.2. Definition and Problem Description
3.3. Preliminaries
4. Density and Location Estimation for Deterministic Deployment
4.1. Dimension Reduction and Analysis
4.2. Deployment Pattern Algorithm for Deterministic Implementation
| Algorithm 1. The Deployment Pattern Algorithm (DPA) |
| INPUT: the ROI A; the parameters of camera nodes OUTPUT: the optimal positions of camera nodes S |
| 1: Establish the virtual grid points set (x, y) from the center (x0, y0) of ROI
2: For each point P in (x, y) 3: Deploy nodes around P with every |
| 4: End |
5. LNSA for Full-View Area Coverage in Random Deployment
| Algorithm 2. The Local Neighbor-optimal Selecting Algorithm (LNSA) |
| INPUT: the position information of all nodes S = {S1, S2, …, Sn} in . OUTPUT: the selected nodes Sb = {S′b1, S′b2, …, S′bi, …, S′bh}. 1: Divide ROI into many regular hexagons H1, H2, …, Hi, …, Ha with the virtual grid points as the center, build the polar coordinate system in Hi 2: Perform the following steps in each regular hexagon Hi 3: Refine the nodes in Hi with and constitute S′c = {Sc1, Sc2, …, Sck} 4: for i = 1: k 5: If 6: Pick the spare nodes from to join S′c 7: i = i − 1 8: End 9: End 10: Choose nodes every as the awakening nodes S′bi = {Sb1, Sb2, …, Sbm} in S′c. |
| 11: End 12: Sb = {S′b1, S′b2, …, S′bi, …, S′bh} |
6. Performance Evaluation
6.1. Simulation Configuration
6.2. Simulations Analysis of DPA
6.3. Performance Evaluation of LNSA
7. Conclusions
Reference
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xiong, N.; Huang, X.; Cheng, H.; Wan, Z. Energy-efficient algorithm for broadcasting in ad hoc wireless sensor networks. Sensors 2013, 13, 4922–4946. [Google Scholar] [CrossRef] [PubMed]
- Xiong, N.; Liu, R.W.; Liang, M.; Wu, D.; Liu, Z.; Wu, H. Effective alternating direction optimization methods for sparsity-constrained blind image deblurring. Sensors 2017, 17, 174. [Google Scholar] [CrossRef] [PubMed]
- Xiao, F.; Xie, X.; Jiang, Z.; Sun, L.; Wang, R. Utility-aware data transmission scheme for delay tolerant networks. Peer-to-Peer Netw. Appl. 2016, 9, 936–944. [Google Scholar] [CrossRef]
- Xiao, F.; Jiang, Z.; Xie, X.; Sun, L.; Wang, R. An energy-efficient data transmission protocol for mobile crowd sensing. Peer-to-Peer Netw. Appl. 2017, 10, 510–518. [Google Scholar] [CrossRef]
- Ai, J.; Abouzeid, A.A. Coverage by directional sensors in randomly deployed wireless sensor networks. J. Comb. Optim. 2006, 11, 21–41. [Google Scholar] [CrossRef]
- Malek, S.M.B.; Sadik, M.M.; Rahman, A. On balanced k-coverage in visual sensor networks. J. Netw. Comput. Appl. 2016, 72, 72–86. [Google Scholar] [CrossRef]
- Mini, S.; Udgata, S.K.; Sabat, S.L. Sensor deployment and scheduling for target coverage problem in wireless sensor networks. J. Netw. Comput. Appl. 2014, 14, 636–644. [Google Scholar] [CrossRef]
- Karakaya, M.; Qi, H. Coverage estimation for crowded targets in visual sensor networks. ACM Trans. Sens. Netw. (TOSN) 2012, 8, 26. [Google Scholar] [CrossRef]
- Younis, M.; Akkaya, K. Strategies and techniques for node placement in wireless sensor networks: A survey. Ad Hoc Netw. 2008, 6, 621–655. [Google Scholar] [CrossRef]
- Costa, D.G.; Silva, I.; Guedes, L.A. Optimal Sensing Redundancy for Multiple Perspectives of Targets in Wireless Visual Sensor Networks. In Proceedings of the IEEE 13th International Conference on Industrial Informatics (INDIN), Cambridge, UK, 22–24 July 2015. [Google Scholar]
- Osais, Y.E.; St-Hilaire, M.; Fei, R.Y. Directional sensor placement with optimal sensing range, field of view and orientation. Mob. Netw. Appl. 2010, 15, 216–225. [Google Scholar] [CrossRef]
- Cai, Y.; Lou, W.; Li, M. Target-oriented scheduling in directional sensor networks. In Proceedings of the 26th IEEE International Conference on Computer Communications, Barcelona, Spain, 6–12 May 2007; pp. 1550–1558. [Google Scholar]
- Ma, H.; Yang, M.; Li, D.; Hong, Y.; Chen, W. Minimum camera barrier coverage in wireless camera sensor networks. In Proceedings of the 31st Annual IEEE International Conference on Computer Communications (IEEE INFOCOM 2012), Orlando, FL, USA, 25–30 March 2012; pp. 217–225. [Google Scholar]
- Zhang, Y.; Sun, X.; Wang, B. Efficient algorithm for k-barrier coverage based on integer linear programming. China Commun. 2016, 13, 16–23. [Google Scholar] [CrossRef]
- Aghdasi, H.S.; Abbaspour, M. Energy efficient area coverage by evolutionary camera node scheduling algorithms in visual sensor networks. Soft Comput. 2015, 20, 1191–1202. [Google Scholar] [CrossRef]
- Yang, Q.; He, S.; Li, J.; Chen, J.; Sun, Y. Energy-efficient probabilistic area coverage in wireless sensor networks. IEEE Trans. Veh. Technol. 2015, 64, 367–377. [Google Scholar] [CrossRef]
- Wang, Y.-C.; Hsu, S.-E. Deploying r&d sensors to monitor heterogeneous objects and accomplish temporal coverage. Pervasive Mob. Comput. 2015, 21, 30–46. [Google Scholar]
- Hu, Y.; Wang, X.; Gan, X. Critical sensing range for mobile heterogeneous camera sensor networks. In Proceedings of the 33rd Annual IEEE International Conference on Computer Communications (INFOCOM’14), Toronto, ON, Canada, 27 April–2 May 2014; pp. 970–978. [Google Scholar]
- He, S.; Shin, D.-H.; Zhang, J.; Chen, J.; Sun, Y. Full-view area coverage in camera sensor networks: Dimension reduction and near-optimal solutions. IEEE Trans. Veh. Technol. 2015, 65, 7448–7461. [Google Scholar] [CrossRef]
- Singh, A.; Rossi, A. A genetic algorithm based exact approach for lifetime maximization of directional sensor networks. Ad Hoc Netw. 2013, 11, 1006–1021. [Google Scholar] [CrossRef]
- Newell, A.; Akkaya, K.; Yildiz, E. Providing multi-perspective event coverage in wireless multimedia sensor networks. In Proceedings of the 35th IEEE Conference on Local Computer Networks (LCN), Denver, CO, USA, 10–14 October 2010; pp. 464–471. [Google Scholar]
- Ng, S.C.; Mao, G.; Anderson, B.D. Critical density for connectivity in 2d and 3d wireless multi-hop networks. IEEE Trans. Wirel. Commun. 2013, 12, 1512–1523. [Google Scholar] [CrossRef]
- Khanjary, M.; Sabaei, M.; Meybodi, M.R. Critical density for coverage and connectivity in two-dimensional fixed-orientation directional sensor networks using continuum percolation. J. Netw. Comput. Appl. 2015, 57, 169–181. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X. 3d percolation theory-based exposure-path prevention for optimal power-coverage tradeoff in clustered wireless camera sensor networks. In Proceedings of the IEEE Global Communications Conference (IEEE Globecom 2014), Austin, TX, USA, 8–12 December 2014; pp. 305–310. [Google Scholar]
- Almalkawi, I.T.; Guerrero Zapata, M.; Al-Karaki, J.N.; Morillo-Pozo, J. Wireless multimedia sensor networks: Current trends and future directions. Sensors 2010, 10, 6662–6717. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.-H.; Chung, Y.-C. A polygon model for wireless sensor network deployment with directional sensing areas. Sensors 2009, 9, 9998–10022. [Google Scholar] [CrossRef] [PubMed]
- Costa, D.G.; Guedes, L.A. The coverage problem in video-based wireless sensor networks: A survey. Sensors 2010, 10, 8215–8247. [Google Scholar] [CrossRef] [PubMed]
- Costa, D.G.; Silva, I.; Guedes, L.A.; Vasques, F.; Portugal, P. Availability issues in wireless visual sensor networks. Sensors 2014, 14, 2795–2821. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Yu, X.; Xu, H.; Qian, J.; Dong, L.; Nie, H. Research on secure localization model based on trust valuation in wireless sensor networks. Secur. Commun. Netw. 2017, 2017, 6102780. [Google Scholar] [CrossRef]
- Mavrinac, A.; Chen, X. Modeling coverage in camera networks: A survey. Int. J. Comput. Vis. 2013, 101, 205–226. [Google Scholar] [CrossRef]
- Guvensan, M.A.; Yavuz, A.G. On coverage issues in directional sensor networks: A survey. Ad Hoc Netw. 2011, 9, 1238–1255. [Google Scholar] [CrossRef]
- Cheng, W.; Li, S.; Liao, X.; Changxiang, S.; Chen, H. Maximal coverage scheduling in randomly deployed directional sensor networks. In Proceedings of the 2007 International Conference on Parallel Processing Workshops (ICPPW 2007), Xi’an, China, 10–14 September 2007; p. 68. [Google Scholar]
- Makhoul, A.; Saadi, R.; Pham, C. Adaptive scheduling of wireless video sensor nodes for surveillance applications. In Proceedings of the 4th ACM Workshop on Performance Monitoring and Measurement of Heterogeneous Wireless and Wired Networks, Tenerife, Spain, 26 October 2009; pp. 54–60. [Google Scholar]
- Gil, J.-M.; Han, Y.-H. A target coverage scheduling scheme based on genetic algorithms in directional sensor networks. Sensors 2011, 11, 1888–1906. [Google Scholar] [CrossRef] [PubMed]
- Sung, T.-W.; Yang, C.-S. Voronoi-based coverage improvement approach for wireless directional sensor networks. J. Netw. Comput. Appl. 2014, 39, 202–213. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, G. On full-view coverage in camera sensor networks. In Proceedings of the 30th IEEE International Conference on Computer Communications (IEEE INFOCOM 2011), Shanghai, China, 10–15 April 2011; pp. 1781–1789. [Google Scholar]
- Wu, Y.; Wang, X. Achieving full view coverage with randomly-deployed heterogeneous camera sensors. In Proceedings of the 2012 IEEE 32nd International Conference on Distributed Computing Systems, Macau, China, 18–21 June 2012; pp. 556–565. [Google Scholar]
- Manoufali, M.; Kong, P.-Y.; Jimaa, S. Effect of realistic sea surface movements in achieving full-view coverage camera sensor network. Int. J. Commun. Syst. 2016, 29, 1091–1115. [Google Scholar] [CrossRef]
- Xiao, F.; Yang, X.; Yang, M.; Sun, L.; Wang, R.; Yang, P. Surface coverage algorithm in directional sensor networks for three-dimensional complex terrains. Tsinghua Sci. Technol. 2016, 21, 397–406. [Google Scholar] [CrossRef]
- Yu, Z.; Yang, F.; Teng, J.; Champion, A.C.; Xuan, D. Local face-view barrier coverage in camera sensor networks. In Proceedings of the 2015 IEEE Conference on Computer Communications (INFOCOM), Hong Kong, China, 26 April–1 May 2015; pp. 684–692. [Google Scholar]
- Zhao, L.; Bai, G.; Jiang, Y.; Shen, H.; Tang, Z. Optimal deployment and scheduling with directional sensors for energy-efficient barrier coverage. Int. J. Distrib. Sens. Netw. 2014, 2014, 596983. [Google Scholar] [CrossRef]
- Tao, D.; Wu, T.-Y. A survey on barrier coverage problem in directional sensor networks. IEEE Sens. J. 2015, 15, 876–885. [Google Scholar]
- Kershner, R. The number of circles covering a set. Am. J. Math. 1939, 61, 665–671. [Google Scholar] [CrossRef]
- Li, X.; Fletcher, G.; Nayak, A.; Stojmenovic, I. Placing sensors for area coverage in a complex environment by a team of robots. ACM Trans. Sens. Netw. 2014, 11, 3. [Google Scholar] [CrossRef]
- Li, F.; Luo, J.; Wang, W.; He, Y. Autonomous deployment for load balancing k-surface coverage in sensor networks. IEEE Trans. Wirel. Commun. 2015, 14, 279–293. [Google Scholar] [CrossRef]












| Reference | Algorithm | Primary Objective | Main Contribution |
|---|---|---|---|
| [36] | FURCA | Full-view area coverage | The safe region and unsafe region |
| [18] | - | Finding critical condition of full-view area coverage | Equivalent sensing radius (ESR) |
| [38] | - | Full-view area coverage | Model the realistic sea surface |
| [19] | DASH | Full-view area coverage | Dimension Reduction |
| [37] | - | Finding critical condition of full-view area coverage | Critical sensing area (CSA) |
| This work | DPA/LNSA | Full-view area coverage | Maximum full-view Neighbor-hood coverage |
| Symbol | Meaning |
|---|---|
| S | Camera node set, S = {S1, S2, …, Sn}, where Si also represent the position of the i-th camera node |
| P | Location of the intruder |
| R | Sensing radius of the camera node |
| r | Radius of the maximum full-view neighborhood coverage disk |
| r′ | Radius of the trajectory for nodes around P |
| One-half of camera’s angle of view | |
| Effective angle | |
| l | Grid length in the triangle lattice-based deployment |
| λ | Sensor density for achieving full-view area coverage |
| Sc | Camera’s field of view (FoV) |
| D(P, r) | Disk with r as the radius and P as the center |
| Tk | The k-th sector |
| Working direction of the i-th camera node | |
| Facial direction of the intruder | |
| Start line for dividing C(P, R) into T1, T2, …, Tk |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, P.-F.; Xiao, F.; Sha, C.; Huang, H.-P.; Wang, R.-C.; Xiong, N.-X. Node Scheduling Strategies for Achieving Full-View Area Coverage in Camera Sensor Networks. Sensors 2017, 17, 1303. https://doi.org/10.3390/s17061303
Wu P-F, Xiao F, Sha C, Huang H-P, Wang R-C, Xiong N-X. Node Scheduling Strategies for Achieving Full-View Area Coverage in Camera Sensor Networks. Sensors. 2017; 17(6):1303. https://doi.org/10.3390/s17061303
Chicago/Turabian StyleWu, Peng-Fei, Fu Xiao, Chao Sha, Hai-Ping Huang, Ru-Chuan Wang, and Nai-Xue Xiong. 2017. "Node Scheduling Strategies for Achieving Full-View Area Coverage in Camera Sensor Networks" Sensors 17, no. 6: 1303. https://doi.org/10.3390/s17061303
APA StyleWu, P.-F., Xiao, F., Sha, C., Huang, H.-P., Wang, R.-C., & Xiong, N.-X. (2017). Node Scheduling Strategies for Achieving Full-View Area Coverage in Camera Sensor Networks. Sensors, 17(6), 1303. https://doi.org/10.3390/s17061303







