An Unobtrusive Fall Detection and Alerting System Based on Kalman Filter and Bayes Network Classifier
Abstract
:1. Introduction
2. Related Work on Wearable Fall Detection
3. Methodology
3.1. Model Activity
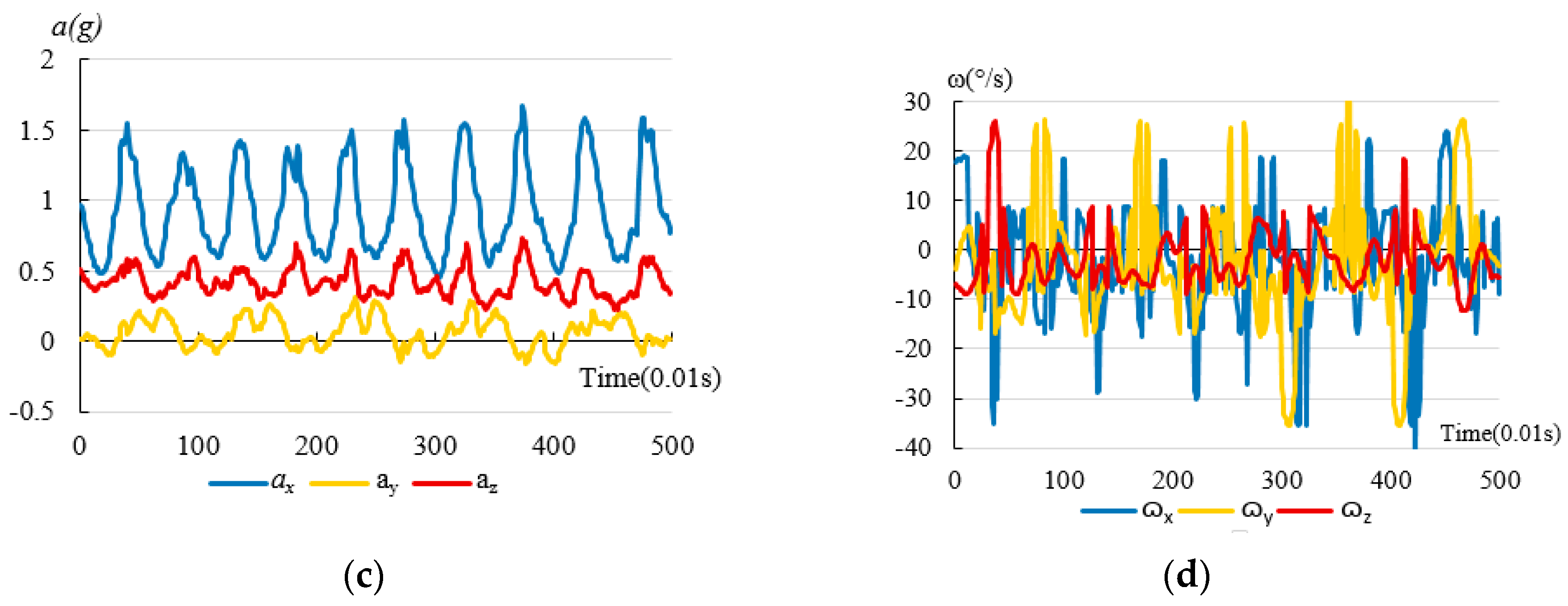
3.2. Data Acquisition
3.3. Filter Noise
3.4. ADLs vs. Falls
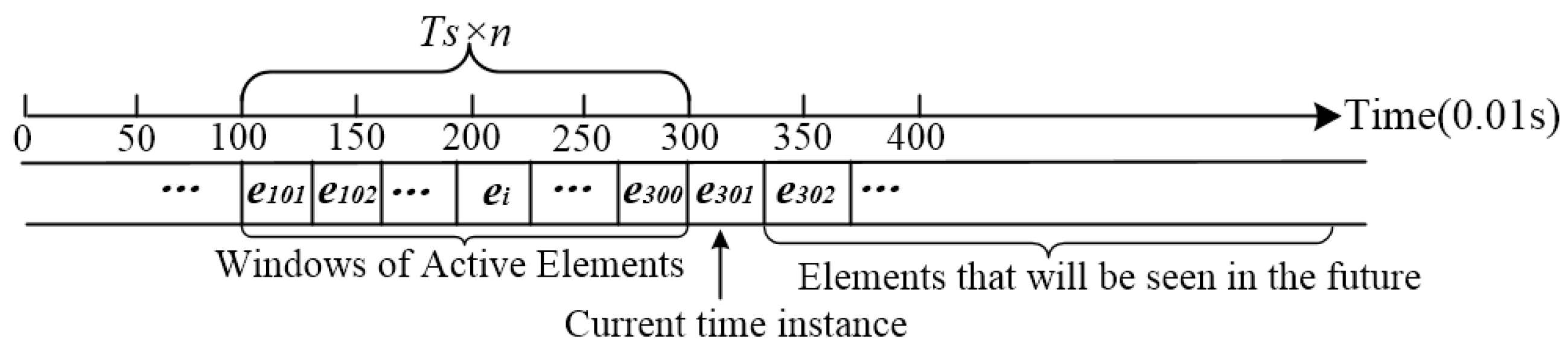
3.5. Feature Extraction
| Algorithm 1 Pseudo-Code Based on the Sliding Window and Bayes Network | |
| 1 | Input: Sensor data stream |
| 2 | Output: Type(label) of a slide instance |
| 3 | label= |
| 4 | Swidth=200, //set the width of sliding window |
| 5 | for (Sref = 0; size (Sref+Swidth) ≥ Swidth; t ++) |
| 6 | label= Bayes network (Dtrain, Sref + Swidth) |
| 7 | end for |
| 8 | return label |
4. Implementation
4.1. Bayes Network Classifier
4.2. Software Design
- Initialize the gyroscope and tri-axial accelerator, set the sampling frequency for the angular velocities, tri-axial accelerations and the baud rate for Bluetooth.
- Sample the angular velocities and accelerations from gyroscope and tri-axial accelerometer at an interval of 0.01 s.
- Send the angular velocities and tri-axial accelerations to the Android smartphone via Bluetooth.
4.3. Software Implementation
5. Experiment
5.1. Experiment Results
5.2. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shumway-Cook, A.; Ciol, M.A.; Hoffman, J.; Dudgeon, B.J.; Yorkston, K.; Chan, L. Falls in the Medicare Population: Incidence, Associated Factors, and Impact on Health Care. Phys. Ther. 2009, 89, 324–332. [Google Scholar] [CrossRef]
- Lord, S.R.; Sherrington, C.; Menz, H.B.; Close, J.C. Falls in Older People: Risk Factors and Strategies for Prevention; Cambridge University Press: Cambridge, UK, 2007; p. 470. [Google Scholar]
- He, J.; Hu, C.; Wang, X.Y. A Smart Device Enabled System for Autonomous Fall Detection and Alert. Int. J. Distrib. Sens. Netw. 2016, 12, 1–10. [Google Scholar] [CrossRef]
- Koshmak, G.; Loutfi, A.; Linden, M. Challenges and Issues in Multisensor Fusion Approach for Fall Detection: Review Paper. J. Sens. 2016, 2016, 1–12. [Google Scholar] [CrossRef]
- Yu, M.; Rhuma, A.; Naqvi, S.M.; Wang, L.; Chambers, J. A posture recognition-based fall detection system for monitoring an elderly person in a smart home environment. IEEE Trans. Inf. Technol. Biomed. 2012, 16, 1274–1286. [Google Scholar]
- Yazar, A.; Erden, F.; Cetin, A.E. Multi-sensor ambient assisted living system for fall detection. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Florence, Italy, 4–9 May 2014; pp. 1–3. [Google Scholar]
- Becker, C.; Schwickert, L.; Mellone, S.; Bagalà, F.; Chiari, L.; Helbostad, J.L.; Zijlstra, W.; Aminian, K.; Bourke, A.; Todd, C.; et al. Proposal for a multiphase fall model based on real-world fall recordings with body-fixed sensors. In Zeitschrift Für Gerontologie Und Geriatrie; Springer International Publishing: Berlin, Germany, 2012; pp. 707–715. [Google Scholar]
- Bai, Y.-W.; Wu, S.-C.; Tsai, C.-L. Design and implementation of a fall monitor system by using a 3-axis accelerometer in a smart phone. IEEE Trans. Consum. Electron. 2012, 58, 1269–1275. [Google Scholar] [CrossRef]
- Salgado, P.; Afonso, P. Fall Detection with Kalman Filter and SVM. In Lecture Notes in Electrical Engineering; Springer: Berlin, Germany, 2015; pp. 407–416. [Google Scholar]
- Medrano, C.; Igual, R.; Plaza, I.; Castro, M.; Fardoun, H.M. Personalizable Smartphone Application for Detecting Falls. In Proceedings of the IEEE-EMBS International Conference on Biomedical and Health Informatics, Valencia, Spain, 1–4 June 2014; pp. 169–172. [Google Scholar]
- El-Sheimy, N.; Hou, H.; Niu, X. Analysis and modeling of inertial sensors using Allan variance. IEEE Trans. Instrum. Meas. 2008, 57, 140–149. [Google Scholar] [CrossRef]
- Pannurat, N.; Thiemjarus, S.; Nantajeewarawat, E. Automatic Fall Monitoring: A review. Sensors 2014, 14, 12900–12936. [Google Scholar] [CrossRef]
- Bourke, A.K.; Van De Ven, P.; Gamble, M.; O’Connor, R.; Murphy, K.; Bogan, E.; McQuade, E.; Finucane, P.; O´Laighin, G.; Nelson, J. Evaluation of waist-mounted tri-axial accelerometer based fall-detection algorithms during scripted and continuous unscripted activities. J. Biomech. 2010, 43, 3051–3057. [Google Scholar] [CrossRef]
- Lindemann, U.; Hock, A.; Stuber, M.; Keck, W.; Becker, C. Evaluation of a fall detector based on accelerometers: A pilot study. Med. Biol. Eng. Comput. 2005, 43, 548–551. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Z.; Li, B.; Lee, S.; Sherratt, R.S. An Enhanced Fall Detection System for Elderly Person Monitoring using Consumer Home Networks. IEEE Trans. Consum. Electron. 2014, 60, 23–28. [Google Scholar] [CrossRef]
- Li, Q.; Stankovic, J.A.; Hanson, M.A.; Barth, A.T.; Lach, J.; Zhou, G. Accurate, fast fall detection using gyroscopes and accelerometer derived posture information. In Body Sensor Networks; International Workshop on Wearable & Implantable Body Sensor Networks: Berkeley, CA, USA, 2009; pp. 138–143. [Google Scholar]
- Gjoreski, H.; Kozina, S.; Gams, M.; Lustrek, M. RAReFall—Real-Time Activity Recognition and Fall Detection System. In Proceedings of the IEEE International Conference on Pervasive Computing and Communications Workshops, Budapest, Hungary, 24–28 March 2014; pp. 145–147. [Google Scholar]
- Özdemir, A.T.; Barshan, B. Detecting falls with wearable sensors using machine learning techniques. Sensors 2014, 14, 10691–10708. [Google Scholar] [CrossRef]
- Ojetola, O.; Gaura, E.I.; Brusey, J. Fall Detection with Wearable Sensors–Safe (Smart Fall Detection). In Proceedings of the 7th International Conference on Intelligent Environments (IE), Nottingham, UK, 25–28 July 2011; pp. 318–321. [Google Scholar]
- Zhang, T.; Wang, J.; Xu, L.; Liu, P. Fall detection by wearable sensor and one-class SVM algorithm. Lect. Notes Control Inf. Sci. 2006, 345, 858–886. [Google Scholar]
- Tong, L.; Song, Q.; Ge, Y.; Liu, M. HMM-Based Human Fall Detection and Prediction Method Using Tri-Axial Accelerometer. IEEE Sens. J. 2013, 13, 1249–1256. [Google Scholar]
- Dinh, C.; Struck, M. A new real-time fall detection approach using fuzzy logic and a neural network. In Proceedings of the International Workshop on Wearable Micro & Nano Technologies for Personalized Health, Oslo, Norway, 24–26 June 2009; pp. 57–60. [Google Scholar]
- Schwickert, L.; Becker, C.; Lindemann, U.; Maréchal, C.; Bourke, A.; Chiari, L.; Helbostad, J.L.; Zijlstra, W.; Aminian, K.; et al. Fall detection with body-worn sensors: A systematic review. In Zeitschrift für Gerontologie Und Geriatrie; Springer: Berlin, Germany, 2013; pp. 706–719. [Google Scholar]
- Ligorio, G.; Sabatini, A.M. A Novel Kalman Filter for Human Motion Tracking with an Inertial-Based Dynamic Inclinometer. IEEE Trans. Biomed. Eng. 2015, 62, 2033–2043. [Google Scholar] [CrossRef]
- Kangas, M.; Vikman, I.; Wiklander, J.; Lindgren, P.; Nyberg, L.; Jämsä, T. Sensitivity and specificity of fall detection in people aged 40 years and over. Gait Posture 2009, 29, 571–574. [Google Scholar] [CrossRef]
- Maryak, J.L.; Spall, J.C.; Heydon, B.D. Use of the Kalman Filter for Inference in State-Space Models with Unknown Noise Distributions. IEEE Trans. Autom. Control 2004, 49, 87–90. [Google Scholar] [CrossRef]
- Brockwell, P.J.; Dahlhaus, R.; Trindade, A.A. Modified Burg Algorithms for Multivariate Subset Autoregression. Stat. Sin. 2005, 15, 197–213. [Google Scholar]
- Friedman, N.; Geiger, D.; Goldszmidt, M. Bayesian network classifiers. Mach. Learn. 1997, 29, 131–163. [Google Scholar] [CrossRef]
- Friedman, N.; Linial, M.; Nachman, I.; Pe’er, D. Using Bayesian Networks to Analyze Expression Data. J. Comput. Biol. 2000, 7, 601–620. [Google Scholar] [CrossRef]
- Klenk, J.; Becker, C.; Lieken, F.; Nicolai, S.; Maetzler, W.; Alt, W.; Zijlstra, W.; Hausdorff, J.M.; Van Lummel, R.C.; Chiari, L.; et al. Comparison of acceleration signals of simulated and real-world backward falls. Med. Eng. Phys. 2011, 33, 368–373. [Google Scholar] [CrossRef]
- Bagala, F.; Becker, C.; Cappello, A.; Chiari, L.; Aminian, K.; Hausdorff, J.M.; Zijlstra, W.; Klenk, J. Evaluation of accelerometer-based fall detection algorithms on real-world falls. PLoS ONE 2012, 7. [Google Scholar] [CrossRef]
- Bourke, A.K.; Klenk, J.; Schwickert, L.; Aminian, K.; Ihlen, EA.; Helbostad, J.L.; Chiari, L.; Becker, C. Temporal and kinematic variables for real-world falls harvested from lumbar sensors in the elderly population. In Proceedings of the 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Milan, Italy, 25–29 August 2015; pp. 5183–5186. [Google Scholar]
- Vavoulas, G.; Pediaditis, M.; Spanakis, E.G.; Tsiknakis, M. The MobiFall dataset: An initial evaluation of fall detection algorithms using smartphones. In Proceedings of the IEEE 13th International Conference on Bioinformatics and Bioengineering, Chania, Greece, 10–13 November 2013; pp. 1–4. [Google Scholar]









| a | x-Axis | y-Axis | z-Axis | ||||||
|---|---|---|---|---|---|---|---|---|---|
| AR(1) | AR(2) | AR(3) | AR(1) | AR(2) | AR(3) | AR(1) | AR(2) | AR(3) | |
| a1 | 0.9974 | 0.5043 | 0.3319 | 1 | 0.5112 | 0.3390 | 0.9953 | 0.5067 | 0.3482 |
| a2 | 0.4944 | 0.3185 | 0.4888 | 0.3080 | 0.4906 | 0.3283 | |||
| a3 | 0.3488 | 0.3526 | 0.3218 | ||||||
| FPE | 4.3205 × 10−5 | 3.2531 × 10−5 | 2.8591 × 10−5 | 3.2978 × 10−5 | 2.5112 × 10−5 | 2.1998 × 10−5 | 5.3838 × 10−5 | 4.0862 × 10−5 | 3.6631 × 10−5 |
| ω | x-Axis | y-Axis | z-Axis | ||||||
|---|---|---|---|---|---|---|---|---|---|
| AR(1) | AR(2) | AR(3) | AR(1) | AR(2) | AR(3) | AR(1) | AR(2) | AR(3) | |
| ω1 | 1 | 0.6655 | 0.5869 | 0.9269 | 0.6346 | 0.5660 | 0.9997 | 0.6819 | 0.6251 |
| ω2 | 0.3345 | 0.1780 | 0.3154 | 0.1767 | 0.3179 | 0.1972 | |||
| ω3 | 0.2350 | 0.2182 | 0.1776 | ||||||
| FPE | 0.0012 | 0.0011 | 0.0010 | 0.0010 | 9.3156 × 10−4 | 8.8745 × 10−4 | 0.0011 | 9.7509 × 10−4 | 9.4564 × 10−4 |
| Test | Total | Correct | Wrong | Accuracy |
|---|---|---|---|---|
| Wk | 100 | 100 | 0 | 100.00% |
| Sq | 100 | 91 | 9 | 91.00% |
| Sd | 100 | 93 | 7 | 93.00% |
| Bw | 100 | 96 | 4 | 96.00% |
| Sd-Fall | 100 | 95 | 5 | 95.00% |
| Bw-Fall | 100 | 99 | 1 | 99.00% |
| Test | Total | Correct | Wrong | Accuracy |
|---|---|---|---|---|
| Wk | 100 | 100 | 0 | 100.00% |
| Sq | 100 | 90 | 10 | 90.00% |
| Sd | 100 | 87 | 13 | 85.00% |
| Bw | 100 | 95 | 5 | 96.00% |
| Sd-Fall | 100 | 94 | 6 | 94.00% |
| Bw-Fall | 100 | 98 | 2 | 97.00% |
| The Number of Features | Accuracy | Sensitivity | Specificity | TP | FP |
|---|---|---|---|---|---|
| 3 | 89.67% | 99.50% | 93.75% | 0.897 | 0.021 |
| 7 | 94.50% | 98.00% | 93.75% | 0.945 | 0.011 |
| 9 | 95.67% | 99.00% | 95.00% | 0.957 | 0.009 |
| Algorithm | Accuracy | Sensitivity | Specificity | Time(s) |
|---|---|---|---|---|
| k-NN; k = 7 | 95.50% | 97.00% | 96.00% | <0.01 |
| Naïve Bayes | 95.50% | 99.50% | 94.25% | 0.24 |
| Bayes Network | 95.67% | 99.00% | 95.00% | 1.33 |
| C4.5 Decision Tree | 92.33% | 99.00% | 91.50% | 1.7 |
| Bagging | 92.17% | 99.00% | 92.75% | 6.11 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Bai, S.; Wang, X. An Unobtrusive Fall Detection and Alerting System Based on Kalman Filter and Bayes Network Classifier. Sensors 2017, 17, 1393. https://doi.org/10.3390/s17061393
He J, Bai S, Wang X. An Unobtrusive Fall Detection and Alerting System Based on Kalman Filter and Bayes Network Classifier. Sensors. 2017; 17(6):1393. https://doi.org/10.3390/s17061393
Chicago/Turabian StyleHe, Jian, Shuang Bai, and Xiaoyi Wang. 2017. "An Unobtrusive Fall Detection and Alerting System Based on Kalman Filter and Bayes Network Classifier" Sensors 17, no. 6: 1393. https://doi.org/10.3390/s17061393
APA StyleHe, J., Bai, S., & Wang, X. (2017). An Unobtrusive Fall Detection and Alerting System Based on Kalman Filter and Bayes Network Classifier. Sensors, 17(6), 1393. https://doi.org/10.3390/s17061393






