A Practical Model of Quartz Crystal Microbalance in Actual Applications
Abstract
:1. Introduction
2. Theory
3. Experimental
4. Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Procek, M.; Stolarczyk, A.; Pustelny, T.; Maciak, E. A Study of a QCM Sensor Based on TiO2 Nanostructures for the Detection of NO2 and Explosives Vapours in Air. Sensors 2015, 15, 9563–9581. [Google Scholar] [CrossRef] [PubMed]
- Qian, K.; Deng, Q.L.; Fang, G.Z.; Wang, J.P.; Pan, M.F.; Wang, S.; Pu, Y.H. Metal-organic frameworks supported surface-imprinted nanoparticles for the sensitive detection of metolcarb. Biosens. Bioelectron. 2016, 79, 359–363. [Google Scholar] [CrossRef] [PubMed]
- Selyanchyn, R.; Korposh, S.; Wakamatsu, S.; Lee, S.W. Respiratory Monitoring by Porphyrin Modified Quartz Crystal Microbalance Sensors. Sensors 2011, 11, 1177–1191. [Google Scholar] [CrossRef] [PubMed]
- Bai, Q.S.; Huang, X.H. Using Quartz Crystal Microbalance for Field Measurement of Liquid Viscosities. J. Sens. 2016, 2016, 7580483. [Google Scholar] [CrossRef]
- Yang, Y.; Tu, Y.F.; Wang, X.S.; Pan, J.Y.; Ding, Y. A Label-Free Immunosensor for Ultrasensitive Detection of Ketamine Based on Quartz Crystal Microbalance. Sensors 2015, 15, 8540–8549. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.H.; Liu, S.L.; Zhang, Y.C.; Yang, Y.Q.; Shi, Y.; He, L.H.; Fang, S.M.; Zhang, Z.H. Graphene nanostructures with plasma polymerized allylamine biosensor for selective detection of mercury ions. Sens. Actuators Chem. B 2014, 203, 497–503. [Google Scholar] [CrossRef]
- Yang, Z.P.; Zhang, C.J. Designing of MIP-based QCM sensor for the determination of Cu(II) ions in solution. Sens. Actuators Chem. B 2009, 142, 210–215. [Google Scholar] [CrossRef]
- Mirmohseni, A.; Pourata, R.; Shojaei, M. Application of Molecularly Imprinted Polymer for Determination of Glucose by Quartz Crystal Nanobalance Technique. IEEE Sens. J. 2014, 14, 2807–2812. [Google Scholar] [CrossRef]
- Zhang, X.R.; Chen, J.; Liu, H.X.; Zhang, S.S. Quartz crystal microbalance detection of protein amplified by nicked circling, rolling circle amplification and biocatalytic precipitation. Biosens. Bioelectron. 2015, 65, 341–345. [Google Scholar] [CrossRef] [PubMed]
- Diltemiz, S.E.; Keçili, R.; Ersöz, A.; Say, R. Molecular Imprinting Technology in Quartz Crystal Microbalance (QCM) Sensors. Sensors 2017, 17, 454. [Google Scholar] [CrossRef] [PubMed]
- Cho, N.J.; Frank, C.W.; Kasemo, B.; Hook, F. Quartz crystal microbalance with dissipation monitoring of supported lipid bilayers on various substrates. Nat. Protoc. 2010, 5, 1096–1106. [Google Scholar] [CrossRef] [PubMed]
- Yao, C.Y.; Qu, L.; Fu, W.L. Detection of Fibrinogen and Coagulation Factor VIII in Plasma by a Quartz Crystal Microbalance Biosensor. Sensors 2013, 13, 6946–6956. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Huang, X.H.; Sun, L.; Xu, L. A piezoelectric immunosensor for the rapid detection of p16 (INK4a) expression in liquid-based cervical cytology specimens. Sens. Actuators Chem. B 2016, 224, 863–867. [Google Scholar] [CrossRef]
- Sauerbrey, G. Use of quartz vibration for weighing thin films on a microbalance. J. Phys. 1959, 155, 206–212. [Google Scholar]
- Kanazawa, K.K. Mechanical behaviour of films on the quartz microbalance. Faraday Discuss. 1997, 107, 77–90. [Google Scholar] [CrossRef]
- Martin, S.J.; Granstaff, V.E.; Frye, G.C. Characterization of a quartz crystal microbalance with simultaneous mass and liquid loading. Anal. Chem. 1991, 63, 2272–2281. [Google Scholar] [CrossRef]
- Huang, X.H.; Bai, Q.S.; Zhou, Q.; Hu, J.G. The Resistance–Amplitude–Frequency Effect of In–Liquid Quartz Crystal Microbalance. Sensors 2017, 17, 1476. [Google Scholar] [CrossRef] [PubMed]
- Martin, S.J.; Bandey, H.I.; Cernosek, R.W.; Hillman, A.R.; Brown, M.J. Equivalent-Circuit Model for the Thickness-Shear Mode Resonator with a Viscoelastic Film Near Film Resonance. Anal. Chem. 2000, 72, 141–149. [Google Scholar] [CrossRef] [PubMed]
- Bai, Q.S.; Huang, X.H. Effective mass layer of a single drop of liquid located on a quartz crystal microbalance. Sens. Mater. 2017, 29, 539–544. [Google Scholar]
- Marx, K.A. Quartz crystal microbalance: A useful tool for studying thin polymer films and complex biomolecular systems at the solution-surface interface. Biomacromolecules 2003, 4, 1099–1120. [Google Scholar] [CrossRef] [PubMed]
- Josse, F.; Lee, Y.; Martin, S.J.; Cernosek, R.W. Analysis of the Radial Dependence of Mass Sensitivity for Modified-Electrode Quartz Crystal Resonators. Anal. Chem. 1998, 70, 237–247. [Google Scholar] [CrossRef]
- Cumpson, P.J.; Seah, M.P. The quartz crystal microbalance; 1 radial/polar dependence of mass sensitivity both on and off the electrodes. Meas. Sci. Technol. 1990, 1, 544–555. [Google Scholar] [CrossRef]
- Gao, J.Y.; Huang, X.H.; Wang, Y. The modified design of ring electrode quartz crystal resonator for uniform mass sensitivity distribution. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 2031–2034. [Google Scholar] [PubMed]
- Lucklum, R.; Hauptmann, P. The quartz crystal microbalance: Mass sensitivity, viscoelasticity and acoustic amplification. Sens. Actuators Chem. B 2000, 70, 30–36. [Google Scholar] [CrossRef]
- Ward, M.D.; Delawski, E.J. Radial mass sensitivity of the quartz crystal microbalance in liquid media. Anal. Chem. 1991, 63, 886–890. [Google Scholar] [CrossRef]
- Oltra, R.; Efimov, I.O. Local sensitivity of an electrochemical quartz crystal microbalance: Spatial location of the low frequency mode. Rev. Sci. Instrum. 1995, 66, 1136–1141. [Google Scholar] [CrossRef]
- Hillier, A.C.; Ward, M.D. Scanning electrochemical mass sensitivity mapping of the quartz crystal microbalance in liquid media. Anal. Chem. 1992, 64, 2539–2554. [Google Scholar] [CrossRef]
- Kawaski, T.; Mochida, T.; Katada, J.; Okahata, Y. Laser response of a quartz crystal microbalance: Frequency changes induced by light irradiation in the air phase. Anal. Sci. 2009, 25, 1069–1075. [Google Scholar] [CrossRef]


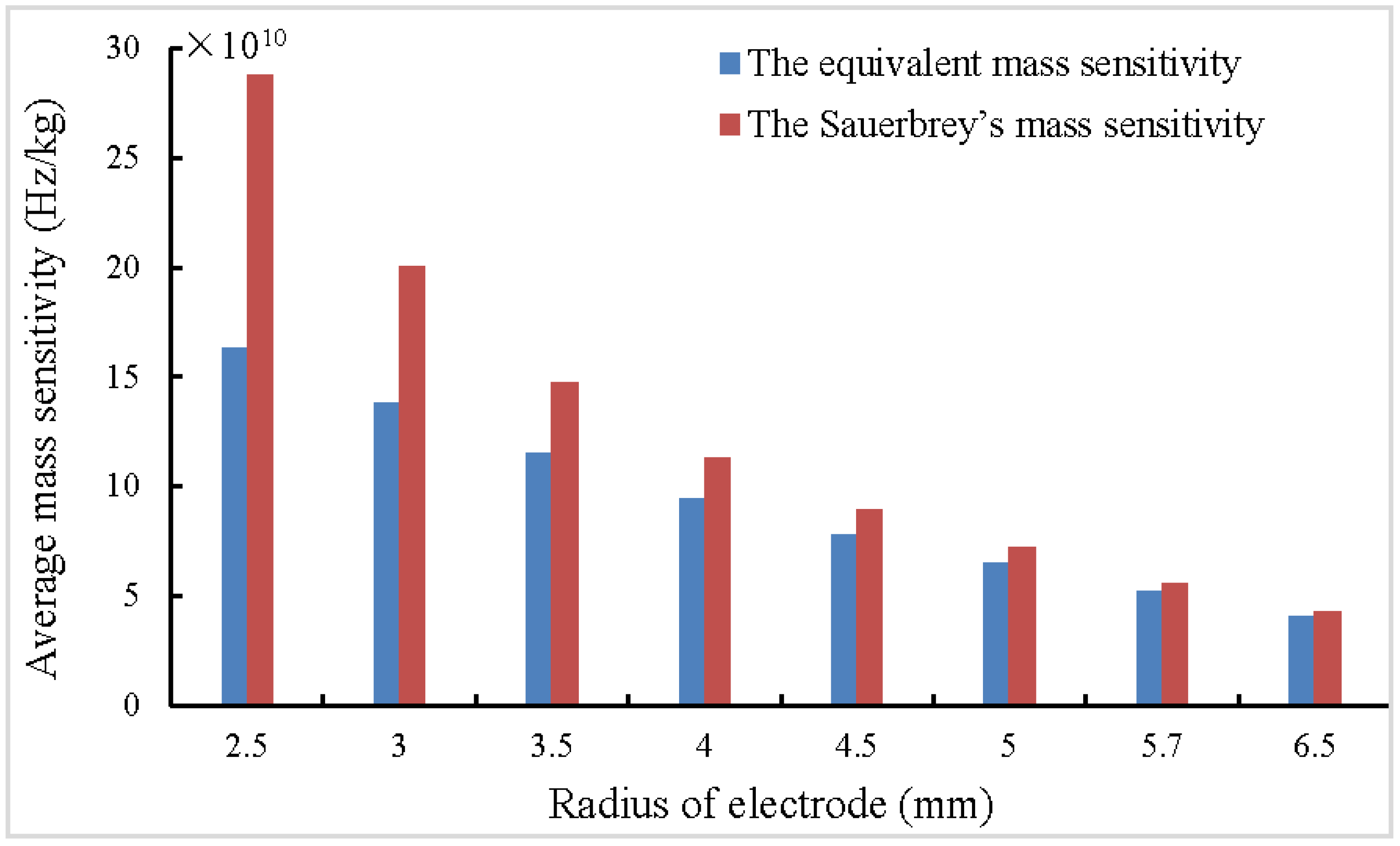

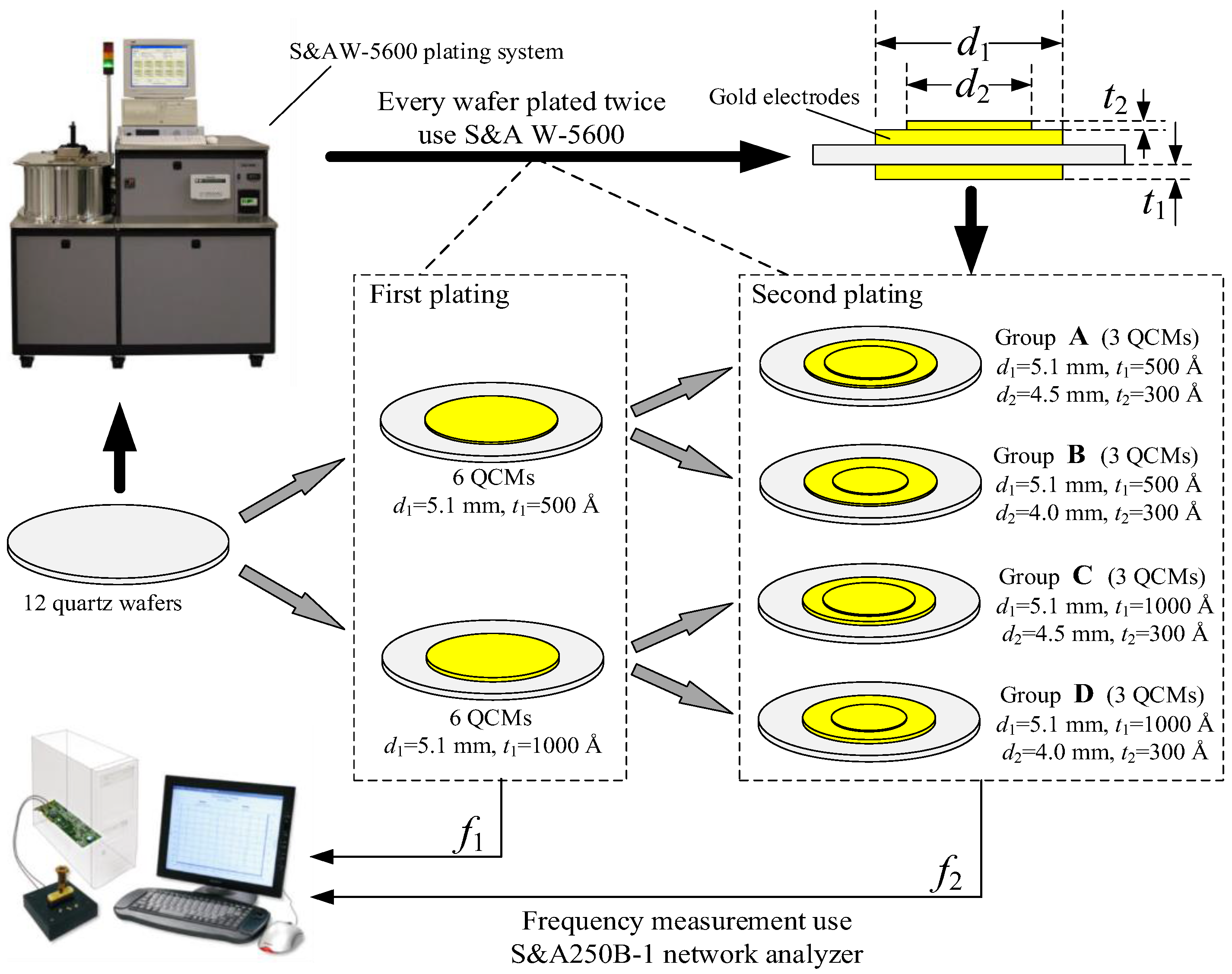
| A | B | C | D | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (Hz) | 10,006,391 | 10,006,821 | 10,004,123 | 10,008,944 | 10,003,835 | 10,005,320 | 9,958,942 | 9,961,677 | 9,961,850 | 9,957,356 | 9,958,215 | 9,956,112 |
| (Hz) | 9,993,685 | 9,994,674 | 9,991,846 | 9,998,311 | 9,993,262 | 9,994,795 | 9,946,278 | 9,949,200 | 9,949,227 | 9,945,483 | 9,946,365 | 9,944,688 |
| (Hz) | 12,706 | 12,147 | 12,277 | 10,633 | 10,573 | 10,525 | 12,664 | 12,477 | 12,623 | 11,873 | 11,850 | 11,424 |
| (Hz) | 12,377 | 10,577 | 12,588 | 11,716 | ||||||||
| (Hz) | 238.84 | 44.18 | 80.25 | 206.45 | ||||||||
| (kg) | 9.22 × 10−9 | 7.28 × 10−9 | 9.22 × 10−9 | 7.28 × 10−9 | ||||||||
| (Hz/kg) | 1.29 × 1012 | 1.50 × 1012 | 1.35 × 1012 | 1.59 × 1012 | ||||||||
| (Hz) | 11,891 | 10,913 | 12,444 | 11,581 | ||||||||
| −3.93% | +3.35% | −1.14% | −1.15% | |||||||||
| (Hz) | 13,120 | 16,596 | 13,120 | 16,596 | ||||||||
| +6.0% | +56.9% | +4.2% | +41.7% | |||||||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Bai, Q.; Hu, J.; Hou, D. A Practical Model of Quartz Crystal Microbalance in Actual Applications. Sensors 2017, 17, 1785. https://doi.org/10.3390/s17081785
Huang X, Bai Q, Hu J, Hou D. A Practical Model of Quartz Crystal Microbalance in Actual Applications. Sensors. 2017; 17(8):1785. https://doi.org/10.3390/s17081785
Chicago/Turabian StyleHuang, Xianhe, Qingsong Bai, Jianguo Hu, and Dong Hou. 2017. "A Practical Model of Quartz Crystal Microbalance in Actual Applications" Sensors 17, no. 8: 1785. https://doi.org/10.3390/s17081785
APA StyleHuang, X., Bai, Q., Hu, J., & Hou, D. (2017). A Practical Model of Quartz Crystal Microbalance in Actual Applications. Sensors, 17(8), 1785. https://doi.org/10.3390/s17081785





