Evaluation of Early-Age Concrete Compressive Strength with Ultrasonic Sensors
Abstract
:1. Introduction
2. Finite Element (FE) Simulation of Surface Wave Propagation
2.1. Objective
2.2. Finite Element Modeling
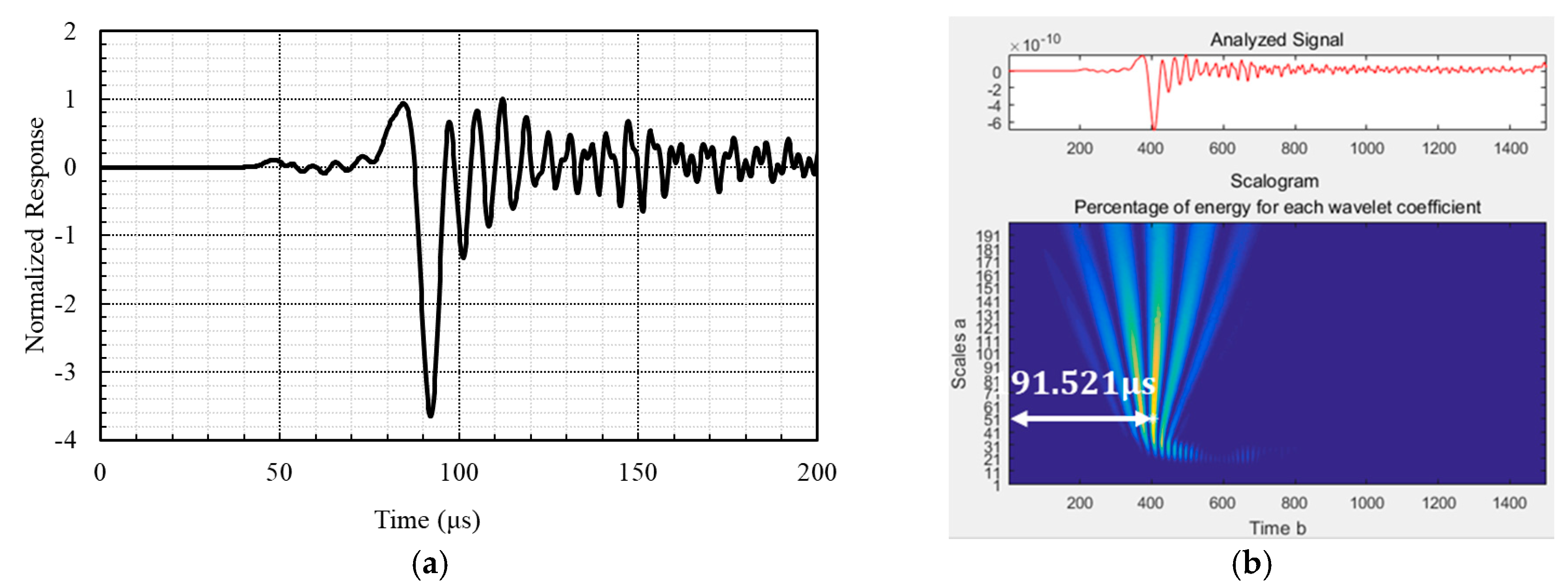
2.3. Signal Processing
2.4. Surface Wave Velocity between the Concrete and Acrylic Layer
3. Measurement of Surface Waves
3.1. Objective
3.2. Experimental Setup and Materials
3.3. Experimental Procedure
4. Experimental Results
4.1. Surface Wave Velocity for Monitoring Early-Age Concrete
4.2. Correlation between the Compressive Strength and Surface Wave Velocity
4.3. Proposed Empirical Formula to Evaluate the Compressive Strength by Using the Surface Wave Velocity
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ministry of Land, Transport and Maritime Affairs. Standard Concrete Specification; Ministry of Land, Transport and Maritime Affairs: Seoul, Korea, 2009.
- Ministry of Land, Infrastructure and Transport. Standard Specification for Temporary Works; Ministry of Land, Infrastructure and Transport: Seoul, Korea, 2014.
- Korea Expressway Corporation Expressway Construction Guide Specification; Korea Expressway Corporation: Seoul, Korea, 2009.
- Korea Concrete Institute. Manual of Concrete Practice; Kimoondang Publishing Co.: Seoul, Korea, 2000. [Google Scholar]
- Building Code Requirement for Structural Concrete and Commentary; ACI Committee 318; American Concrete Institute: Farmington Hills, MI, USA, 2014.
- Guide to Formwork for Concrete; ACI Committee 347; American Concrete Institute: Farmington Hills, MI, USA, 2014.
- US Army Corps of Engineers. EM 1110-1-2009: Engineering and Design—Architectural Concrete; US Army Corps of Engineers: Washington, DC, USA, 1997. [Google Scholar]
- Gu, H.; Song, G.; Dhonde, H.; Mo, Y.L.; Yan, S. Concrete early-age strength monitoring using embedded piezoelectric transducers. Smart Mate. Struct. 2006, 15, 1837. [Google Scholar] [CrossRef]
- Dumoulin, C.; Karaiskos, G.; Carette, J.; Staquet, S.; Deraemaeker, A. Monitoring of the ultrasonic P-wave velocity in early-age concrete with embedded piezoelectric transducers. Smart Mater. Struct. 2012, 21. [Google Scholar] [CrossRef]
- Kong, Q.; Hou, S.; Ji, Q.; Mo, Y.L.; Song, G. Very early age concrete hydration characterization monitoring using piezoceramic based smart aggregates. Smart Mater. Struct. 2013, 22. [Google Scholar] [CrossRef]
- Shin, S.W.; Qureshi, A.R.; Lee, J.Y.; Yun, C.B. Piezoelectric sensor based nondestructive active monitoring of strength gain in concrete. Smart Mater. Struct. 2008, 17. [Google Scholar] [CrossRef]
- Shin, S.W.; Oh, T.K. Application of electro-mechanical impedance sensing technique for online monitoring of strength development in concrete using smart PZT patches. Constr. Build. Mater. 2009, 23, 1185–1188. [Google Scholar] [CrossRef]
- Tawie, R.; Lee, H.K. Monitoring the strength development in concrete by EMI sensing technique. Constr. Build. Mater. 2010, 24. [Google Scholar] [CrossRef]
- Reinhardt, H.W.; Grosse, C.U. Advanced Testing of Cement-Based Materials during Setting and Hardening. Final Report of RILEM TC 185-ATC; RILEM Publications: Paris, France, 2005. [Google Scholar]
- Standard Test Method for Pulse Velocity through Concrete; ASTM Standard C597; ASTM Committee C09.64; ASTM International: West Conshohocken, PA, USA, 2016.
- Kim, J.H.; Kwak, H. Rayleigh wave velocity computation using principal wavelet-component analysis. NDT E Int. 2011, 44, 47–56. [Google Scholar] [CrossRef]
- Popovics, J.S.; Abraham, O. Surface wave techniques for evaluation of concrete structures. In Non-Destructive Evaluation of Reinforced Concrete Structures; Woodhead Publishing Ltd.: Washington DC, USA, 2010; Volume 2, pp. 441–465. [Google Scholar]
- Shin, S.W.; Yun, C.B.; Popovics, J.S.; Kim, J.H. Improved Rayleigh wave velocity measurement for nondestructive early-age concrete monitoring. Res. Nondestr. Eval. 2007, 18, 45–68. [Google Scholar] [CrossRef]
- Popovics, J.; Song, W.; Achenbach, J.; Lee, J.; Andre, R. One-sided stress wave velocity measurement in concrete. J. Eng. Mech. 1998, 124, 1346–1353. [Google Scholar] [CrossRef]
- Gallo, G.E.; Popovics, J.S. The use of surface waves to estimate in situ concrete strength. J. Adv. Concr. Technol. 2005, 3, 355–362. [Google Scholar] [CrossRef]
- Lim, Y.Y.; Kwong, K.Z.; Liew, W.Y.H.; Soh, C.K. Non-destructive concrete strength evaluation using smart piezoelectric transducer—A comparative study. Smart Mater. Struct. 2016, 25. [Google Scholar] [CrossRef]
- Moser, F.; Jacobs, L.J.; Qu, J. Modeling elastic wave propagation in waveguides with the finite element method. NDT E Int. 1999, 32, 225–234. [Google Scholar] [CrossRef]
- Wu, T.-T.; Fang, J.-S.; Liu, G.-Y.; Kuo, M.-K. Determination of elastic constants of a concrete specimen using transient elastic waves. J. Acoust. Soc. Am. 1995, 98, 2142–2148. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Miller, G.; Pursey, H. On the partition of energy between elastic waves in a semi-infinite solid. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1955, 233, 55–69. [Google Scholar] [CrossRef]
- Kishimoto, K.; Inoue, H.; Hamada, M.; Shibuya, T. Time frequency analysis of dispersive waves by means of wavelet transform. J. Appl. Mech. 1995, 62, 841–846. [Google Scholar] [CrossRef]
- Inoue, H.; Kishimoto, K.; Shibuya, T. Experimental wavelet analysis of flexural waves in beams. Exp. Mech. 1996, 36, 212–217. [Google Scholar] [CrossRef]
- Kim, Y.Y.; Kim, E.H. A new damage detection method based on a wavelet transform. In Proceedings of the 18th IMAC, San Antonio, TX, USA, 7–10 February 2000. [Google Scholar]
- McGetrick, P.J.; Kim, C.W. A Parametric Study of a Drive by Bridge Inspection System Based on the Morlet Wavelet. Key Eng. Mater. 2013, 569–570, 262–269. [Google Scholar] [CrossRef]
- Testing Method for Time of Setting of Concrete Mixture by Penetration Resistance; Korean Standards KS F 2436; Korean Agency for Technology and Standards (KATS): Seoul, Korea, 2007.
- Korean Standards KS F 2403. Standard Test Method for Making and Curing Concrete Specimens; Korean Agency for Technology and Standards (KATS): Seoul, Korea, 2014. [Google Scholar]
- Ministry of Land, Transport and Maritime Affairs. Korean Highway Bridge. Design Code (Limit State Design); Korea Road and Transportation Association: Seoul, Korea, 2015.
- Kheder, G.F. A two stage procedure for assessment of in situ concrete strength using combined non-destructive testing. Mater. Struct. 1999, 32, 410–417. [Google Scholar] [CrossRef]
- Pessiki, S.P.; Carino, N.J. Setting time and concrete strength using the impact-echo method. ACI Mater. J. 1989, 85, 389–399. [Google Scholar]
- Turgut, P. Evaluation of the ultrasonic pulse velocity data coming on the field. In Proceedings of the 4th International Conference on NDE in Relation to Structural Integrity for Nuclear and Pressurized Components, London, UK, 6–8 December 2004. [Google Scholar]
- Nash’t, I.H.; Saeed, H.A.; Sadoon, A.A. Finding a unified relationship between crushing concrete strength and non-destructive tests. In Proceedings of the 3rd MENDT—Middle East Nondestructive Testing Conference & Exhibition, Manama, Bahrain, 27–30 November 2005. [Google Scholar]
- Trtnik, G.; Kavčič, F.; Turk, G. Prediction of concrete strength using ultrasonic pulse velocity and artificial neural networks. Ultrasonics 2009, 49, 53–60. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, H.K.; Yim, H.; Lee, K.M. Velocity-strength relationship of concrete by impact-echo method. Mater. J. 2003, 100, 49–54. [Google Scholar]













| Case | Specification | Start Time (µs) | Arrival Time (µs) | Velocity (m/s) | Difference (%) | |
|---|---|---|---|---|---|---|
| Case 1: effect of acrylic layer | Rayleigh wave (without acrylic) | 3.2 | 119.846 | 857.29 | 100 | |
| Surface wave (with acrylic) | 3.2 | 116.327 | 883.96 | 103.1 | ||
| Case 2: effect of concrete density | Density (kg/m3) | 2200 | 3.2 | 114.992 | 894.52 | 100 |
| 2250 | 3.2 | 116.292 | 884.24 | 98.9 | ||
| 2300 | 3.2 | 117.577 | 874.30 | 97.7 | ||
| 2350 | 3.2 | 118.550 | 866.93 | 96.9 | ||
| 2400 | 3.2 | 119.805 | 857.60 | 95.9 | ||
| Case 3: effect of Poisson’s ratio | Poisson’s ratio | 0.16 | 3.2 | 116.327 | 883.96 | 100 |
| 0.20 | 3.2 | 117.364 | 879.05 | 99.4 | ||
| 0.28 | 3.2 | 119.454 | 875.93 | 99.1 | ||
| 0.30 | 3.2 | 119.805 | 872.31 | 98.7 | ||
| 0.35 | 3.2 | 121.134 | 860.55 | 97.4 | ||
| Index | Type | W/C (%) | S/A (%) | Unit Weight (kg/m3) | Curing Temperature (°C) | Design Strength (MPa) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fly Ash | Super-Plasticizer | Cement | Sand | Gravel | |||||||
| 1 | OPC | MIX1-T35 | 35.4 | 46 | - | 4.75 | 475 | 760 | 935 | 35 | 40 |
| 2 | MIX1-T30 | 30 | |||||||||
| 3 | MIX1-T20 | 20 | |||||||||
| 4 | MIX1-T15 | 15 | |||||||||
| 5 | MIX1-T05 | 5 | |||||||||
| 6 | SC | MIX2-T35 | 35.4 | 46 | - | 4.75 | 475 | 760 | 935 | 35 | 40 |
| 7 | MIX2-T30 | 30 | |||||||||
| 8 | MIX2-T20 | 20 | |||||||||
| 9 | MIX2-T15 | 15 | |||||||||
| 10 | MIX2-T05 | 5 | |||||||||
| 11 | FA | MIX3-T35 | 38 | 42 | 104 | 7 | 419 | 672 | 932 | 35 | 40 |
| 12 | MIX3-T30 | 30 | |||||||||
| 13 | MIX3-T20 | 20 | |||||||||
| 14 | MIX3-T15 | 15 | |||||||||
| 15 | MIX3-T05 | 5 | |||||||||
| 16 | HPC | MIX4-T35 | 39.2 | 45 | - | 4.2 | 420 | 674.3 | 827.9 | 35 | 80 |
| 17 | MIX4-T30 | 30 | |||||||||
| 18 | MIX4-T20 | 20 | |||||||||
| 19 | MIX4-T15 | 15 | |||||||||
| 20 | MIX4-T05 | 5 | |||||||||
| Type | Required Time (h) | Type | Required Time (h) | ||
|---|---|---|---|---|---|
| Initial Setting | Final Setting | Initial Setting | Final Setting | ||
| MIX1-T35 | 3.7 | 5.3 | MIX3-T35 | 3.9 | 5.8 |
| MIX1-T30 | 4.6 | 6.1 | MIX3-T30 | 4.2 | 6.3 |
| MIX1-T20 | 6.4 | 8.8 | MIX3-T20 | 5.0 | 7.8 |
| MIX1-T15 | 7.3 | 10.2 | MIX3-T15 | 6.6 | 10.2 |
| MIX1-T05 | 11.2 | 16.6 | MIX3-T05 | 8.1 | 14.7 |
| MIX2-T35 | 5.0 | 6.5 | MIX4-T35 | 3.6 | 6.9 |
| MIX2-T30 | 4.9 | 7.3 | MIX4-T30 | 4.0 | 7.2 |
| MIX2-T20 | 7.4 | 10.9 | MIX4-T20 | 5.4 | 9.0 |
| MIX2-T15 | 9.2 | 13.0 | MIX4-T15 | 4.8 | 10.1 |
| MIX2-T05 | 12.7 | 19.4 | MIX4-T05 | 8.1 | 16.7 |
| Type | Temperature (°C) | K | R2 | Type | Temperature (°C) | K | R2 |
|---|---|---|---|---|---|---|---|
| MIX1 | 30–35 | 1.2394 | 0.874 | MIX3 | 30–35 | 2.4437 | 0.925 |
| 15–20 | 1.0955 | 0.901 | 15–20 | 1.1207 | 0.567 | ||
| 5 | 0.52677 | 0.934 | 5 | 0.64678 | 0.982 | ||
| MIX2 | 30–35 | 1.1981 | 0.939 | MIX4 | 30–35 | 2.3002 | 0.846 |
| 15–20 | 0.83825 | 0.95 | 15–20 | 1.0433 | 0.943 | ||
| 5 | 0.40681 | 0.961 | 5 | 0.41227 | 0.975 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, H.; Kim, Y.J.; Kim, H.S.; Kang, J.W.; Koh, H.-M. Evaluation of Early-Age Concrete Compressive Strength with Ultrasonic Sensors. Sensors 2017, 17, 1817. https://doi.org/10.3390/s17081817
Yoon H, Kim YJ, Kim HS, Kang JW, Koh H-M. Evaluation of Early-Age Concrete Compressive Strength with Ultrasonic Sensors. Sensors. 2017; 17(8):1817. https://doi.org/10.3390/s17081817
Chicago/Turabian StyleYoon, Hyejin, Young Jin Kim, Hee Seok Kim, Jun Won Kang, and Hyun-Moo Koh. 2017. "Evaluation of Early-Age Concrete Compressive Strength with Ultrasonic Sensors" Sensors 17, no. 8: 1817. https://doi.org/10.3390/s17081817
APA StyleYoon, H., Kim, Y. J., Kim, H. S., Kang, J. W., & Koh, H.-M. (2017). Evaluation of Early-Age Concrete Compressive Strength with Ultrasonic Sensors. Sensors, 17(8), 1817. https://doi.org/10.3390/s17081817




