A Robust Inner and Outer Loop Control Method for Trajectory Tracking of a Quadrotor
Abstract
1. Introduction
2. Dynamic Model
3. Trajectory Tracking Control
3.1. Trajectory Tracking Control
3.2. Attitude Control
4. Simulations
4.1. Parameter Selection
4.2. Trajectory Tracking Simulation
4.2.1. Trajectory Tracking
4.2.2. Trajectory Tracking in Presence of Model Uncertainty and Disturbances
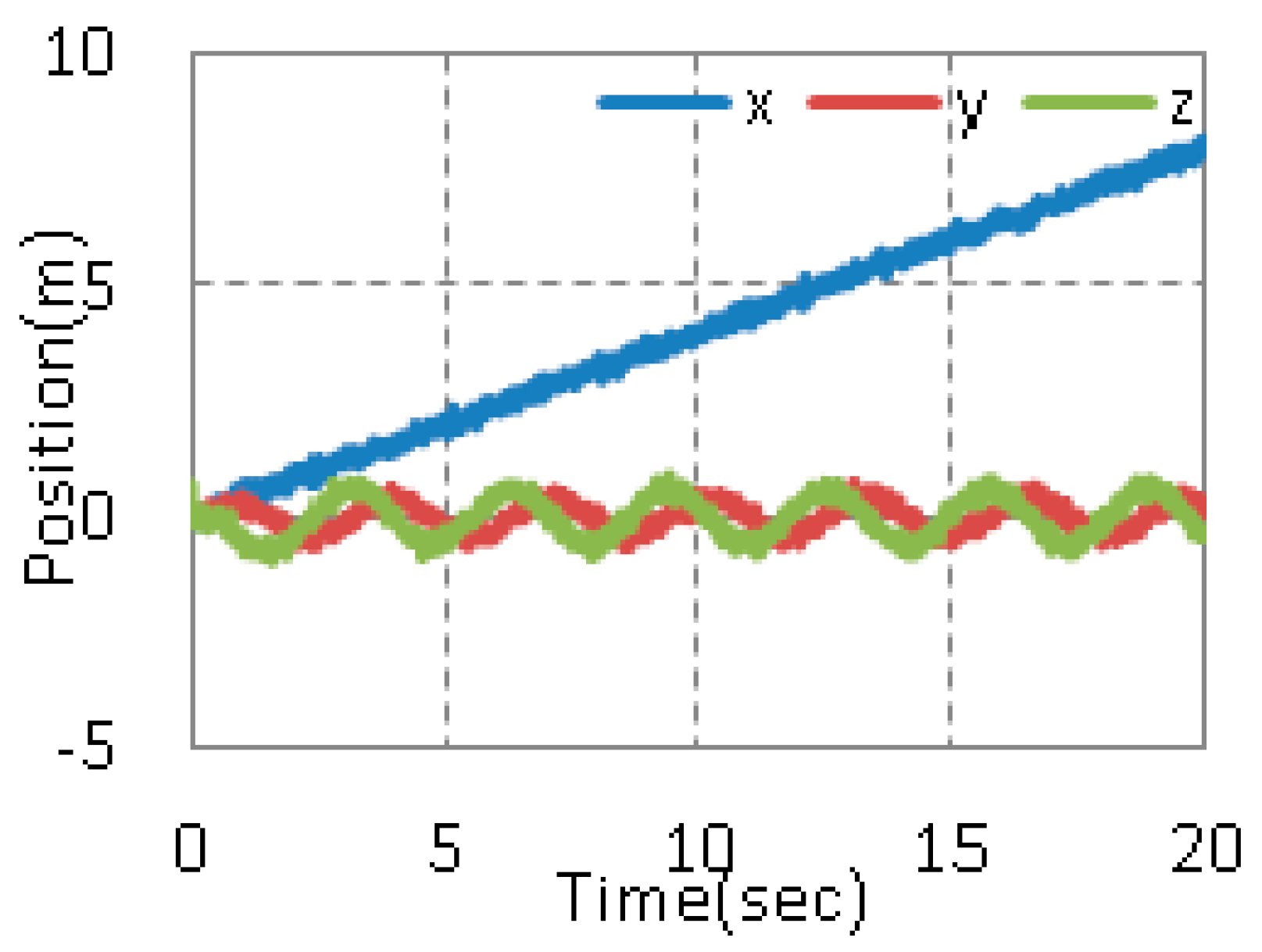
5. Experimental Results
5.1. Experimental Setup
| Algorithm 1: Extended Kalman Filter |
| Given the initial state and initial covariance matrix , update the state estimation as follows Compute the predicted state: Compute the process model Jacobian matrix : Compute the predicted covariance matrix : Compute the Kalam gain: Update the state estimation: Update the covariance matrix: |
5.2. Experimental Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bouabdallah, S. Design and Control of Quadrotors with Application to Autonomous Flying. Ph.D. Thesis, Ecole Polytechnique Federale de Lausanne, Lausanne, Switzerland, 2007. [Google Scholar]
- Olivares-Mendez, M.A.; Fu, C.H. Towards an autonomous vision-based unmanned aerial system against wildlife poachers. Sensors 2015, 15, 31362–31363. [Google Scholar] [CrossRef] [PubMed]
- Hua, M.D.; Hamel, T.; Morin, P.; Samson, C. Introduction to feedback control of underactuated VTOL vehicles: A review of basic control design ideas and principles. IEEE Control Syst. Mag. 2013, 33, 61–75. [Google Scholar]
- Ozbek, N.S.; Onkol, M.; Efe, M.O. Feedback control strategies for quadrotor-type aerial robots: A survey. Trans. Inst. Meas. Control 2015, 38, 1–26. [Google Scholar]
- He, Z.F.; Zhao, L. Quadrotor Trajectory Tracking Based on Quasi-LPV System and Internal Model Control. Math. Probl. Eng. 2015, 2015, 1–13. [Google Scholar] [CrossRef]
- Nicol, C.; Macnab, C.J.B.; Ramirez-Serrano, A. Robust neural network control of a quadrotor helicopter. In Proceedings of the CCECE 2008-Canadian Conference on Electrical and Computer Engineering, Niagara Falls, ON, Canada, 4–7 May 2008; pp. 1233–1238. [Google Scholar]
- González-Vázquez, S.; Moreno-Valenzuela, J. Motion control of a quadrotor aircraft via singular perturbations. Int. J. Adv. Robot. Syst. 2013, 10, 1–17. [Google Scholar]
- Tayebi, A.; Mcgilvray, S. Attitude Stabilization of a VTOL Quadrotor Aircraft. IEEE Trans. Control Syst. Technol. 2006, 14, 1–11. [Google Scholar] [CrossRef]
- Diao, C.; Xian, B.; Zhao, B.; Zhang, X.; Liu, S. An output feedback attitude tracking controller design for quadrotor unmanned aerial vehicles using quaternion. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 3051–3056. [Google Scholar]
- Guerrero-Sanchez, M.; Abaunza, H.; Castillo, P.; Lozano, R.; Garcia-Beltran, C.; Rodriguez, P. Passivity-Based control for a Micro Air Vehicle using unit quaternions. Appl. Sci. 2016, 7, 13. [Google Scholar] [CrossRef]
- Lee, T.; Leok, M.; McClamroch, N.H. Geometric tracking control of a quadrotor UAV on SE(3). In Proceedings of the 49th IEEE Conference on Decision and Control, Atlanta, GA, USA, 15–17 December 2010; pp. 1–6. [Google Scholar]
- Goodarzi, F.; Lee, D.; Lee, T. Geometric nonlinear PID control of a quadrotor UAV on SE(3). In Proceedings of the 2013 European Control Conference, Zurich, Switzerland, 17–19 July 2013; pp. 1–6. [Google Scholar]
- Mellinger, D. Trajectory Generation and Control for Quadrotors. Ph.D. Thesis, University of Pennsylvania, Philadelphia, PA, USA, 2012. [Google Scholar]
- Bullo, F.; Murray, R.M. Tracking for fully actuated mechanical systems: A geometric framework. Automatica 1999, 35, 17–34. [Google Scholar] [CrossRef]
- Xu, R.; Özgüner, Ü. Sliding mode control of a class of under actuated systems. Automatica 2008, 44, 233–241. [Google Scholar] [CrossRef]
- Xiong, J.J.; Zheng, E.H. Position and attitude control for a quadrotor UAV. ISA Trans. 2014, 53, 725–731. [Google Scholar] [CrossRef] [PubMed]
- Cao, N.; Lynch, A.F. Inner-Outer Loop Control for Quadrotor UAVs with Input and State Constraints. IEEE Trans. Control Syst. Technol. 2016, 24, 1797–1804. [Google Scholar] [CrossRef]
- Cao, N.; Lynch, A.F. Inner-outer loop control with constraints for rotary-wing UAVs. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems, Denver, CO, USA, 9–12 June 2015; pp. 294–302. [Google Scholar]
- Smith, J.; Su, J.; Liu, C.; Chen, W.H. Disturbance observer based control with anti-windup applied to a small fixed wing UAV for disturbance rejection. J. Intell. Robot. Syst. 2017, 1–3. [Google Scholar] [CrossRef]
- Eker, L. Second-order sliding mode control with experimental application. ISA Trans. 2010, 49, 394–405. [Google Scholar] [CrossRef] [PubMed]
- Shtessel, Y.; Taleb, M.; Plestan, F. A novel adaptive-gain supertwisting sliding mode controller: Methodology and application. Automatica 2012, 48, 759–760. [Google Scholar] [CrossRef]
- Fridman, L.; Moreno, J.A.; Bandyopadhyay, B. Continuous Nested Algorithms: The fifth generation of sliding mode controllers. In Recent Advances in Sliding Modes: From Control to Intelligent Mechatronics; Springer International Publishing: Berlin, Germany, 2015; pp. 5–33. [Google Scholar]
- Yang, J.; Li, S.; Su, J.; Yu, X. Continuous nonsingular terminal sliding mode control for systems with mismatched disturbances. Automatica 2013, 49, 2287–2289. [Google Scholar] [CrossRef]
- Su, J.; Yang, J.; Li, S. Continuous finite-time anti-disturbance control for a class of uncertain nonlinear system. Trans. Inst. Meas. Control 2014, 36, 300–302. [Google Scholar] [CrossRef]
- Murray, R.M.; Sastry, S.S.; Zexiang, L. A Mathematical Introduction to Robotic Manipulation; CRC Press: Boca Raton, FL, USA, 1994; pp. 69–71. [Google Scholar]
- Fantoni, I.; Lozano, R.; Kendoul, F. Asymptotic stability of hierarchical inner-outer loop-based flight controllers. In Proceedings of the 17th World Congress the International Federation of Automatic Control, Seoul, Korea, 6–11 July 2008; pp. 1741–1746. [Google Scholar]
- Wang, L.; Jia, H. The trajectory tracking problem of quadrotor UAV: Global stability analysis and control design based on the cascade theory. Asian J. Control 2014, 16, 574–588. [Google Scholar] [CrossRef]
- Ailon, A.; Arogeti, S. Closed-form nonlinear tracking controller for quadrotors with model and input generator uncertainities. Automatica 2015, 54, 317–324. [Google Scholar] [CrossRef]
- Song, Y.; Nuske, S.; Scherer, S. A multi-sensor fusion MAV state estimation from long-range stereo, IMU, GPS and barometric sensors. Sensors 2016, 17, 11. [Google Scholar] [CrossRef] [PubMed]
- Xia, D.; Kong, L.; Hu, Y.; Ni, P. Silicon microgyroscope temperature prediction and control system based on bp neural network and fuzzy-pid control method. Meas. Sci. Technol. 2015, 26, 025101. [Google Scholar] [CrossRef]
- Shen, C.; Bai, Z.; Cao, H. Optical flow sensor/ins/magnetometer integrated navigation system for MAV in GPS-denied environment. J. Sens. 2016, 2016, 1–10. [Google Scholar]
- Weiss, S.; Achtelik, M.W.; Lynen, S.; Chli, M. Real-time onboard visual-inertial state estimation and self-calibration of MAVs in unknown environments. IEEE Int. Conf. Robot. Autom. 2012, 44, 957–964. [Google Scholar]
- Weiss, S.; Siegwart, R. Real-time metric state estimation for modular vision-inertial systems. IEEE Int. Conf. Robot. Automation 2011, 19, 4531–4537. [Google Scholar]
- Mahony, R.; Hamel, T.; Pflimlin, J.M. Nonlinear complementary filters on the special orthogonal group. IEEE Trans. Autom. Control 2008, 53, 1203–1218. [Google Scholar] [CrossRef]
- Zhang, X.; Xian, B.; Zhao, B.; Zhang, Y. Autonomous flight control of a Nano Quadrotor helicopter in a GPS-Denied environment using on-board vision. IEEE Trans. Ind. Electron. 2015, 62, 6392–6403. [Google Scholar] [CrossRef]
- Choi, Y.C.; Ahn, H.S. Nonlinear control of quadrotor for point tracking: Actual implementation and experimental tests. IEEE/ASME Trans. Mechatron. 2015, 20, 1179–1193. [Google Scholar] [CrossRef]

















| Name | Variable | Value | Units |
|---|---|---|---|
| Mass | M | 2.0 | kg |
| Arm length | L | 0.20 | m |
| Inertia on x axis | 1.25 | ||
| Inertia on y axis | 1.25 | ||
| Inertia on z axis | 2.5 | ||
| Drag coefficients | 0.012 |
| Case 1 | 10 | 10 | 10 | 1 | 1 | 1 | 0.1 | 0.1 | 0.1 |
| Case 2 | 10 | 10 | 10 | 5 | 5 | 5 | 0.1 | 0.1 | 0.1 |
| Case 3 | 10 | 10 | 10 | 1 | 1 | 1 | 1 | 1 | 1 |
| Case 4 | 12 | 12 | 12 | 1 | 1 | 1 | 0.1 | 0.1 | 0.1 |
| IAE | ISE | ISCI | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Case 1 | 0.9682 | 0.3469 | 1.0215 | 0.4407 | 0.0845 | 0.3788 | 0.3028 | 0.3809 | 38.9353 |
| Case 2 | 0.6981 | 0.3435 | 0.6408 | 0.2748 | 0.1024 | 0.2152 | 0.0275 | 0.1890 | 38.6488 |
| Case 3 | 0.7641 | 0.2911 | 0.7862 | 0.3699 | 0.0791 | 0.3035 | 0.2422 | 0.3760 | 38.8503 |
| Case 4 | 1.2993 | 0.4847 | 1.3257 | 0.5999 | 0.1073 | 0.5238 | 0.5210 | 0.4912 | 39.3407 |
| Index | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Cases | MAE | IAE | ISE | MAE | IAE | ISE | MAE | IAE | ISE | |
| Case 1 | PD + PD | 1 | 1.2819 | 0.6831 | 0.5441 | 0.8947 | 0.2843 | 1.0052 | 1.1981 | 0.6336 |
| SMC + SMC | 1 | 1.0367 | 0.6080 | 0.2608 | 0.3024 | 0.0535 | 1.0017 | 1.0085 | 0.5592 | |
| Case 2 | PD + PD | 1 | 1.6168 | 0.7109 | 0.5465 | 1.2783 | 0.3123 | 1.0052 | 1.4237 | 0.6357 |
| SMC + SMC | 1 | 1.1433 | 0.6104 | 0.2607 | 0.4089 | 0.0541 | 1.0017 | 1.0469 | 0.5601 | |
| Sensor | Gyroscope | Accelerometer | Magnetometer |
|---|---|---|---|
| Type | MPU6000 | MPU6000 | LSM303D |
| Full scale | −1000~1000 (°/s) | −8~+8 (g) | −8~+8 (gauss) |
| Sensitivity | 0.030 (°/s/LSB) | 0.2 (mg/LSB) | 0.320 (mGauss/LSB) |
| Index | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parameters | MO | IAE | ISE | MO | IAE | ISE | MO | IAE | ISE | |
| 16 | 0.2551 | 1.5721 | 0.1943 | 0.2415 | 2.1305 | 0.4862 | 0.1766 | 1.9916 | 0.4019 | |
| 5.6 | ||||||||||
| 16 | 0.1263 | 1.6070 | 0.2033 | 0.1576 | 2.0041 | 0.3983 | 0.1637 | 1.9363 | 0.3997 | |
| 10 | ||||||||||
| 18 | 0.1502 | 1.5100 | 0.1819 | 0.1074 | 1.9805 | 0.3766 | 0.084 | 1.9285 | 0.3883 | |
| 10 | ||||||||||
| Controller | SMC + SMC | PD + PD | |||||
|---|---|---|---|---|---|---|---|
| Index | |||||||
| Case 1 | Settling time [s] | 3.39 | 3.42 | 4.49 | 5.29 | 5.30 | 6.44 |
| Range [m] | (−0.25,0.26) | (−0.41,0.31) | (−0.76,0.32) | (−0.31,0.32) | (−0.72,0.41) | (−0.78,0.42) | |
| The percentage of error within 0.2 m | 98.3% | 95.6% | 92. 7% | 94.3% | 87.8 % | 89.4 % | |
| Standard deviation [m] | 0.0921 | 0.1006 | 0.1353 | 0.09724 | 0.1514 | 0.1396 | |
| Case 2 | Settling time [s] | 3.43 | 3.45 | 4.53 | 5.69 | 5.68 | 6.83 |
| Range [m] | (−0.31,0.35) | (−0.43,0.33) | (−0.77,0.34) | (−0.38,0.45) | (−0.73,0.46) | (−0.79,0.53) | |
| The percentage of error within 0.2 m | 96.2% | 93.8% | 90.8% | 88.0% | 80.4% | 78.2% | |
| Standard deviation [m] | 0.0935 | 0.1018 | 0.1364 | 0.1283 | 0.1698 | 0.1738 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, D.; Cheng, L.; Yao, Y. A Robust Inner and Outer Loop Control Method for Trajectory Tracking of a Quadrotor. Sensors 2017, 17, 2147. https://doi.org/10.3390/s17092147
Xia D, Cheng L, Yao Y. A Robust Inner and Outer Loop Control Method for Trajectory Tracking of a Quadrotor. Sensors. 2017; 17(9):2147. https://doi.org/10.3390/s17092147
Chicago/Turabian StyleXia, Dunzhu, Limei Cheng, and Yanhong Yao. 2017. "A Robust Inner and Outer Loop Control Method for Trajectory Tracking of a Quadrotor" Sensors 17, no. 9: 2147. https://doi.org/10.3390/s17092147
APA StyleXia, D., Cheng, L., & Yao, Y. (2017). A Robust Inner and Outer Loop Control Method for Trajectory Tracking of a Quadrotor. Sensors, 17(9), 2147. https://doi.org/10.3390/s17092147




