A High Sensitivity Electric Field Microsensor Based on Torsional Resonance
Abstract
:1. Introduction
2. Working Principle and Structure Design
2.1. Working Principle
2.2. Structure Design
3. Simulation and Optimization
3.1. Electric Field Distribution
3.2. Parameter Optimization
3.3. Resonant Mode Simulation
4. Analysis of Charge Induction Efficiency
- (a)
- Increasing k. The optimization of the sensitive structure design will be helpful, such as adopting coplanar interdigital electrodes and out-of-plane vibration.
- (b)
- Increasing θ0. The amplitude of the torsional angle can be raised by raising the driving voltages. However, the torsional angle is limited because of the pull-in effect.
- (c)
- Increasing excitation frequency ω. However, for this resonant microsensor, it is best to work at resonant frequency for gaining the largest torsional angle θ0.
5. Fabrication
- (a)
- Metal layer is deposited on the glass substrate as driving electrodes.
- (b)
- Deep reactive ion etching (DRIE) is used to form a cavity on the device silicon of an SOI wafer.
- (c)
- The anodic bonding of the SOI wafer and the glass substrate is conducted.
- (d)
- The substrate silicon and SiO2 layers are removed completely.
- (e)
- Metal pads are deposited on the device silicon layer as an ohmic contact.
- (f)
- DRIE is used to pattern the device structure, with the shielding electrodes and the sensing electrodes included.
6. Experiments
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Vaillancourt, G.H.; Carignan, S.; Jean, C. Experience with the detection of faulty composite insulators on high-voltage power lines by the electric field measurement method. IEEE Trans. Power Deliv. 1998, 13, 661–666. [Google Scholar] [CrossRef]
- Gerrard, C.A.; Gibson, J.R.; Jones, G.R.; Holt, L.; Simkin, D. Measurements of power system voltages using remote electric field monitoring. IEE Proc. Gen. Trans. Distrib. 1998, 145, 217–224. [Google Scholar] [CrossRef]
- Hornfeldt, S.P. DC-probes for electric field distribution measurements. IEEE Trans. Power Deliv. 1991, 11, 524–529. [Google Scholar] [CrossRef]
- Zeng, Q.; Wang, Z.; Guo, F.; Feng, M.; Zhou, S.; Wang, H.; Xu, D. The application of lightning forecasting based on surface electrostatic field observations and radar data. J. Electrost. 2013, 71, 6–13. [Google Scholar] [CrossRef]
- Schumann, C.; Silva, R.B.G.D.; Schulz, W. Electric fields changes produced by positives cloud-to-ground lightning flashes. J. Atmos. Sol.-Terr. Phys. 2013, 92, 37–42. [Google Scholar] [CrossRef]
- Ferro, M.A.D.S.; Yamasaki, J.; Pimentel, D.R.M.; Naccarato, K.P.; Saba, M.M.F. Lightning risk warnings based on atmospheric electric field measurements in Brazil. J. Aerosp. Technol. Manag. 2011, 3, 301–310. [Google Scholar] [CrossRef]
- Evans, W.H. The measurement of electric fields in clouds. Pure Appl. Geophys. 1965, 62, 191–197. [Google Scholar] [CrossRef]
- Liao, J.T.; Peng, Z.R.; Zhang, L.X.; Zhang, S.; Li, N.; Li, J. Electric field distribution on four-bundle conductors in 750 kV AC substation. In Proceedings of the IEEE 10th International Conference on Properties and Applications of Dielectric Materials (ICPADM2012), Bangalore, India, 1–4 July 2012. [Google Scholar]
- Hsu, C.H.; Muller, R.S. Micromechanical electrostatic voltmeter. In Proceedings of the International Conference on Solid-State Sensors and Actuators, San Francisco, CA, USA, 24–27 June 1991. [Google Scholar]
- Zhu, Y.; Lee, E.Y.; Seshia, A.A. A resonant micromachined electrostatic charge sensor. IEEE Sens. J. 2008, 8, 1499–1505. [Google Scholar]
- Peng, C.; Chen, X.; Bai, Q.; Luo, L.; Xia, S. A novel high performance micromechanical resonant electrostatic field sensor used in atmospheric electric field detection. In Proceedings of the IEEE International Conference on MICRO Electro Mechanical Systems, Las Vegas, NV, USA, 22–26 January 2006. [Google Scholar]
- Chen, X.; Peng, C.; Xia, S. Design of a thermally driven resonant miniature electric field sensor with feedback control. In Proceedings of the IEEE International Conference on Nano/micro Engineered and Molecular Systems, Sanya, China, 6–9 January 2008. [Google Scholar]
- Riehl, P.S.; Scott, K.L.; Muller, R.S.; Howe, R.T.; Yasaitis, J.A. Electrostatic charge and field sensors based on micromechanical resonators. J. Microelectromechanical Syst. 2003, 12, 577–589. [Google Scholar] [CrossRef]
- Gong, C.; Tao, H.; Peng, C.; Bai, Q.; Chen, S.; Xia, S. A novel miniature interlacing vibrating electric field sensor. In Proceedings of the IEEE Sensors, Irvine, CA, USA, 30 October–3 November 2005. [Google Scholar]
- Yang, P.; Peng, C.; Zhang, H.; Liu, S.; Fang, D.; Xia, S. A high sensitivity SOI electric-field sensor with novel comb-shaped microelectrodes. In Proceedings of the 16th International Solid-State Sensors, Actuators and Microsystems Conference, Beijing, China, 5–9 June 2011. [Google Scholar]
- Horenstein, M.N.; Stone, P.R. A micro-aperture electrostatic field mill based on MEMS technology. J. Electrost. 2001, 51, 515–521. [Google Scholar] [CrossRef]
- Bahreyni, B.; Wijeweera, G.; Shafai, C.; Rajapakse, A. Design and testing of a field-chopping electric field sensor using thermal actuators with mechanically amplified response. In Proceedings of the Solid-State Sensors, Actuators and Microsystems Conference, Lyon, France, 10–14 June 2007. [Google Scholar]
- Bahreyni, B.; Wijeweera, G.; Shafai, C.; Rajapakse, A. Analysis and design of a micromachined electric-field sensor. J. Microelectromechanical Syst. 2008, 17, 31–36. [Google Scholar] [CrossRef]
- Wu, X.; Wang, X.; Yan, X.; Lin, L. A novel high-sensitivity electrostatic biased electric field sensor. J. Micromechanics Microengineering 2015, 25. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, D.; Feng, K.; Ren, R.; Chen, B.; Peng, C.; Xia, S. A novel micro electric field sensor with X–Y, dual axis sensitive differential structure. Sens. Actuators A 2015, 229, 1–7. [Google Scholar] [CrossRef]
- Ma, Q.; Huang, K.; Yu, Z.; Wang, Z. An electric field sensor with double-layer floating structure for measurement of dc synthetic field coupled with ion flow. In Proceedings of the International Conference on Solid-State Sensors, Actuators and Microsystems, Kaohsiung, Taiwan, 18–22 June 2017. [Google Scholar]
- Bao, M.; Yang, H. Squeeze film air damping in MEMS. Sens. Actuators A 2007, 136, 3–27. [Google Scholar] [CrossRef]
- Pan, F.; Kubby, J.; Peeters, E.; Tran, A.T.; Mukherjee, S. Squeeze film damping effect on the dynamic response of a MEMS torsion mirror. J. Micromechanics Microengineering 1998, 8, 474–479. [Google Scholar] [CrossRef]





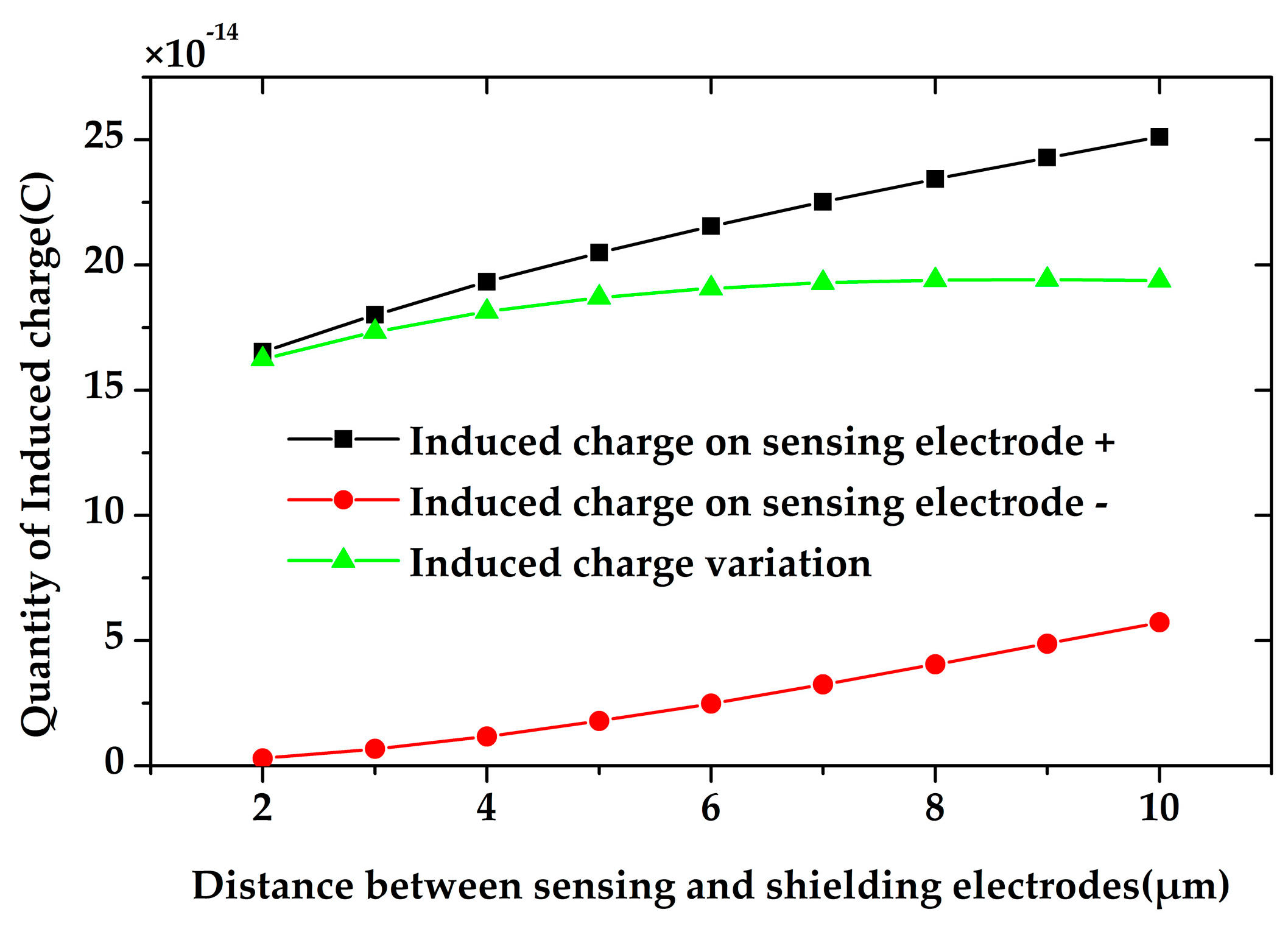

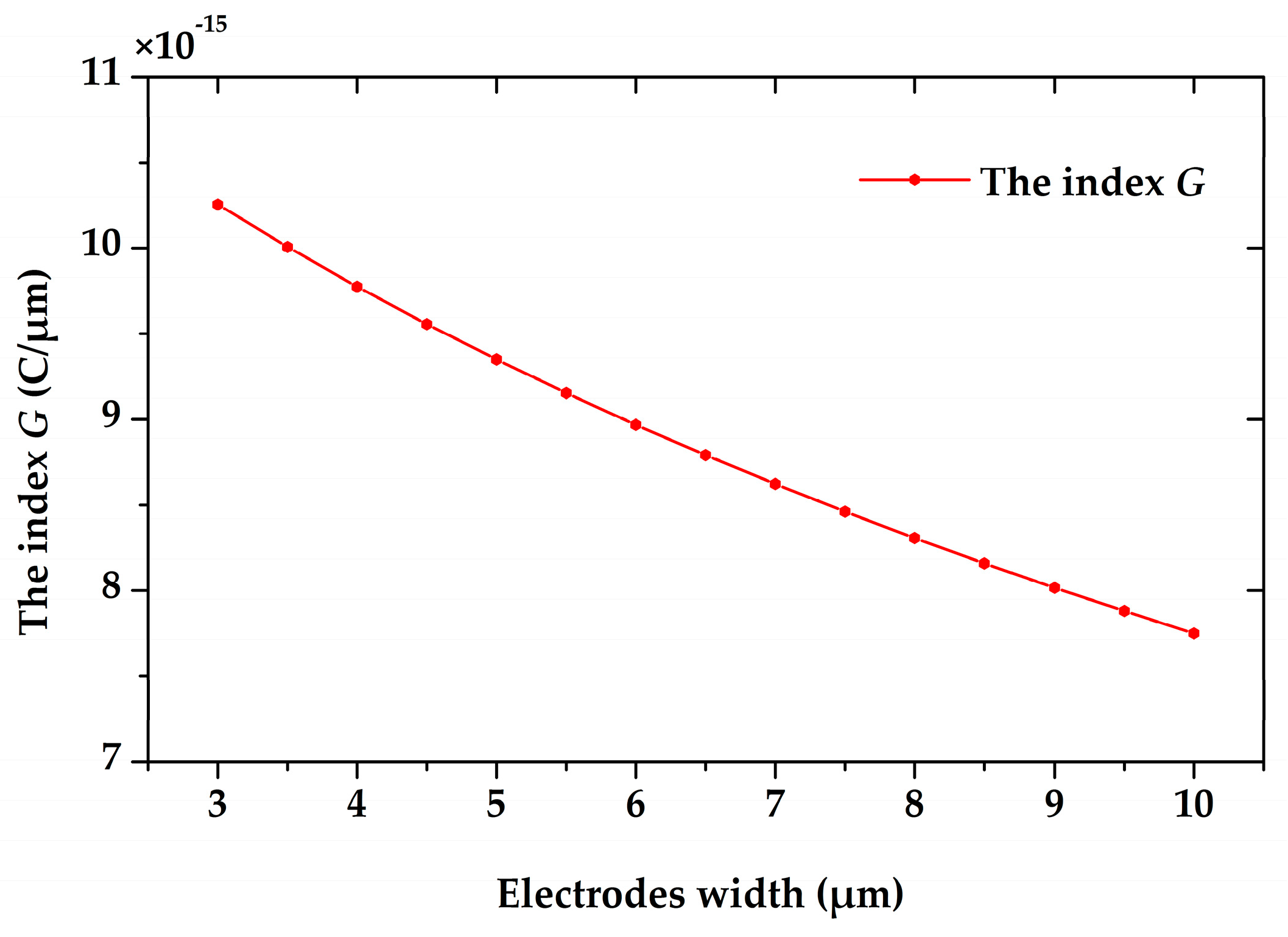









| Symbol | Structural Parameters | Value |
|---|---|---|
| τ | thickness of the sensitive structure | 10 µm |
| d | distance between the sensitive structure and substrate | 15 µm |
| W | width of the driving elements | 1900 µm |
| L | length of the driving elements | 500 µm |
| wt | width of the torsional beam | 20 µm |
| lt | length of the torsional beam | 100 µm |
| w | width of the electrodes | 5 µm |
| l | length of the electrodes | 500 µm |
| g | gap between the electrodes | 5 µm |
| Ne | number of the sensing electrodes | 94 × 2 |
| lh | side length of the square holes | 30 µm |
| Nh | number of the square holes | 217 × 2 |
| Qe | induced charge variation on single electrode (with the shielding electrodes’ maximum displacement of 10 µm) | 5.98 × 10−17 C |
| Data Resources | Conditions | Sensitivity |
|---|---|---|
| Experimental result | Tested in open air | 4.82 mV/(kV/m) |
| Simulation result 1 | The maximum displacement of shielding electrodes is 7 µm | 4.67 mV/(kV/m) |
| Simulation result 2 | The maximum displacement of shielding electrodes is 8 µm | 5.16 mV/(kV/m) |
| Simulation result 3 | The maximum displacement of shielding electrodes is 10 µm | 6.02 mV/(kV/m) |
| EFMs | Year | Sensitivity |
|---|---|---|
| MEMS field mill [16] | 2001 | 40 nV/(kV/m) |
| EFM using thermal actuators [17] | 2007 | 0.1 mV/(kV/m) |
| Thermally driven resonant EFM [12] | 2008 | 0.098 mV/(kV/m) |
| Micromachined EFM [18] | 2008 | 0.15 mV/(kV/m) |
| SOI EFM [15] | 2011 | 0.2 mV/(kV/m) |
| Electrostatic biased EFM [19] | 2015 | 0.84 mV/(kV/m) |
| EFM in this paper | 2017 | 4.82 mV/(kV/m) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, Z.; Peng, C.; Ren, R.; Ling, B.; Zhang, Z.; Lei, H.; Xia, S. A High Sensitivity Electric Field Microsensor Based on Torsional Resonance. Sensors 2018, 18, 286. https://doi.org/10.3390/s18010286
Chu Z, Peng C, Ren R, Ling B, Zhang Z, Lei H, Xia S. A High Sensitivity Electric Field Microsensor Based on Torsional Resonance. Sensors. 2018; 18(1):286. https://doi.org/10.3390/s18010286
Chicago/Turabian StyleChu, Zhaozhi, Chunrong Peng, Ren Ren, Biyun Ling, Zhouwei Zhang, Hucheng Lei, and Shanhong Xia. 2018. "A High Sensitivity Electric Field Microsensor Based on Torsional Resonance" Sensors 18, no. 1: 286. https://doi.org/10.3390/s18010286
APA StyleChu, Z., Peng, C., Ren, R., Ling, B., Zhang, Z., Lei, H., & Xia, S. (2018). A High Sensitivity Electric Field Microsensor Based on Torsional Resonance. Sensors, 18(1), 286. https://doi.org/10.3390/s18010286





