Composite Hierarchical Anti-Disturbance Control with Multisensor Fusion for Compact Optoelectronic Platforms
Abstract
:1. Introduction
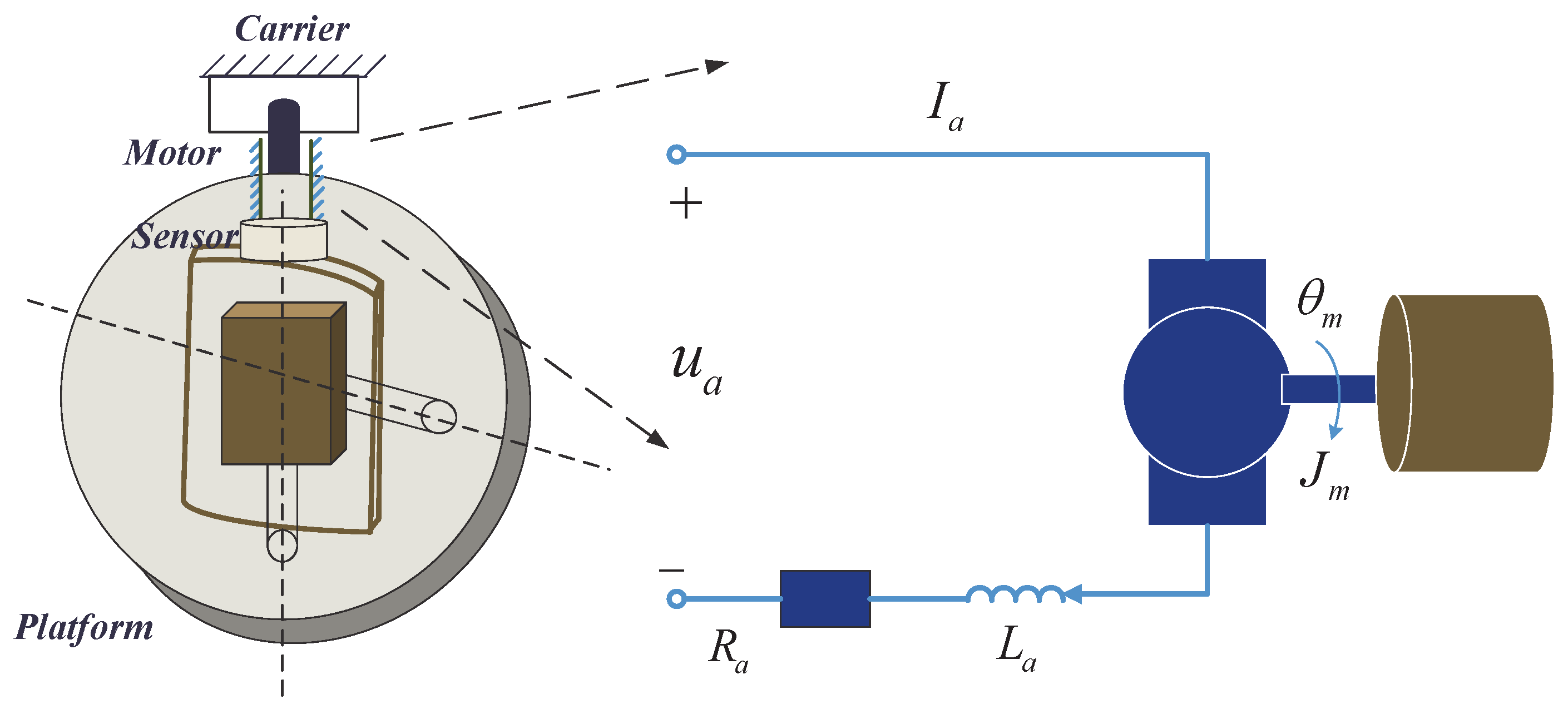
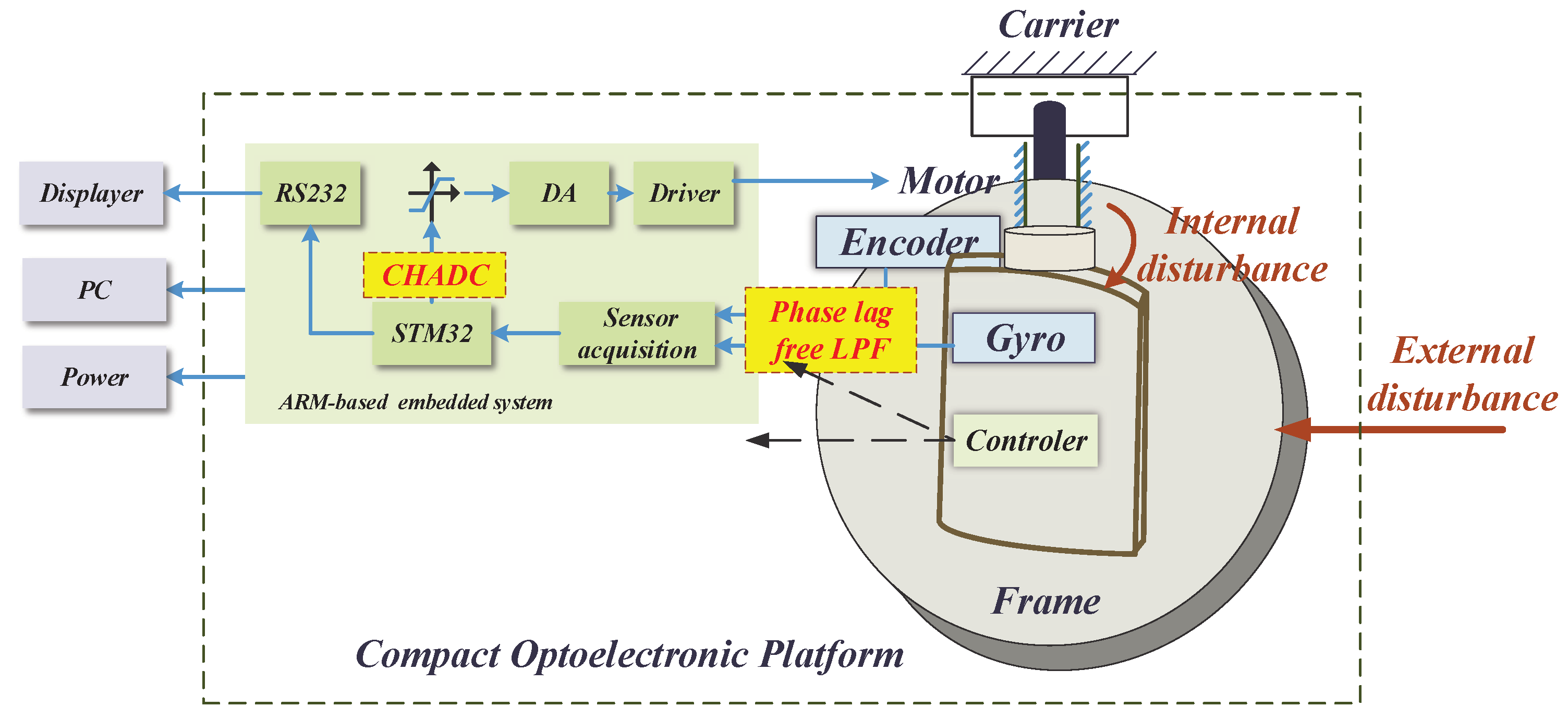
2. Modelling of the Compact Optoelectronic Platform
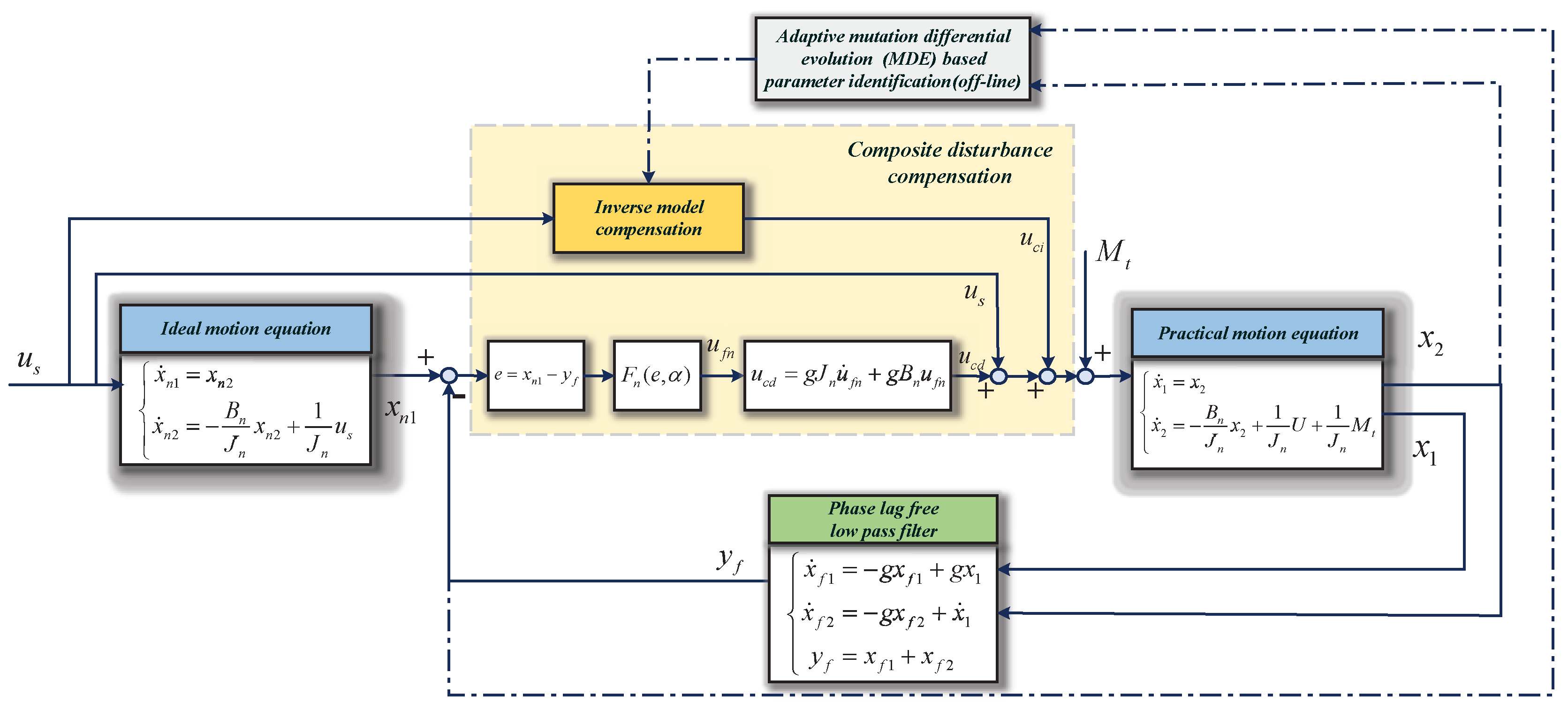
3. Control Strategy Design of Composite Hierarchical Anti-Disturbance Control
3.1. Composite Disturbance Identification, Modelling and Compensation
3.1.1. Internal Disturbance Identification, Modelling and Compensation
3.1.2. Finite-Time Disturbance Observer
- (1)
- V is a positive definite function;
- (2)
- the arithmetic number c and a satisfy and , respectively. The open neighbourhood containing the origin satisfies . If the following condition is established,then, the system shown in Equation (42) is finite-time stable. If , and is radial unbounded, then the system is globally finite-time stable. In addition, the convergence time T satisfies .
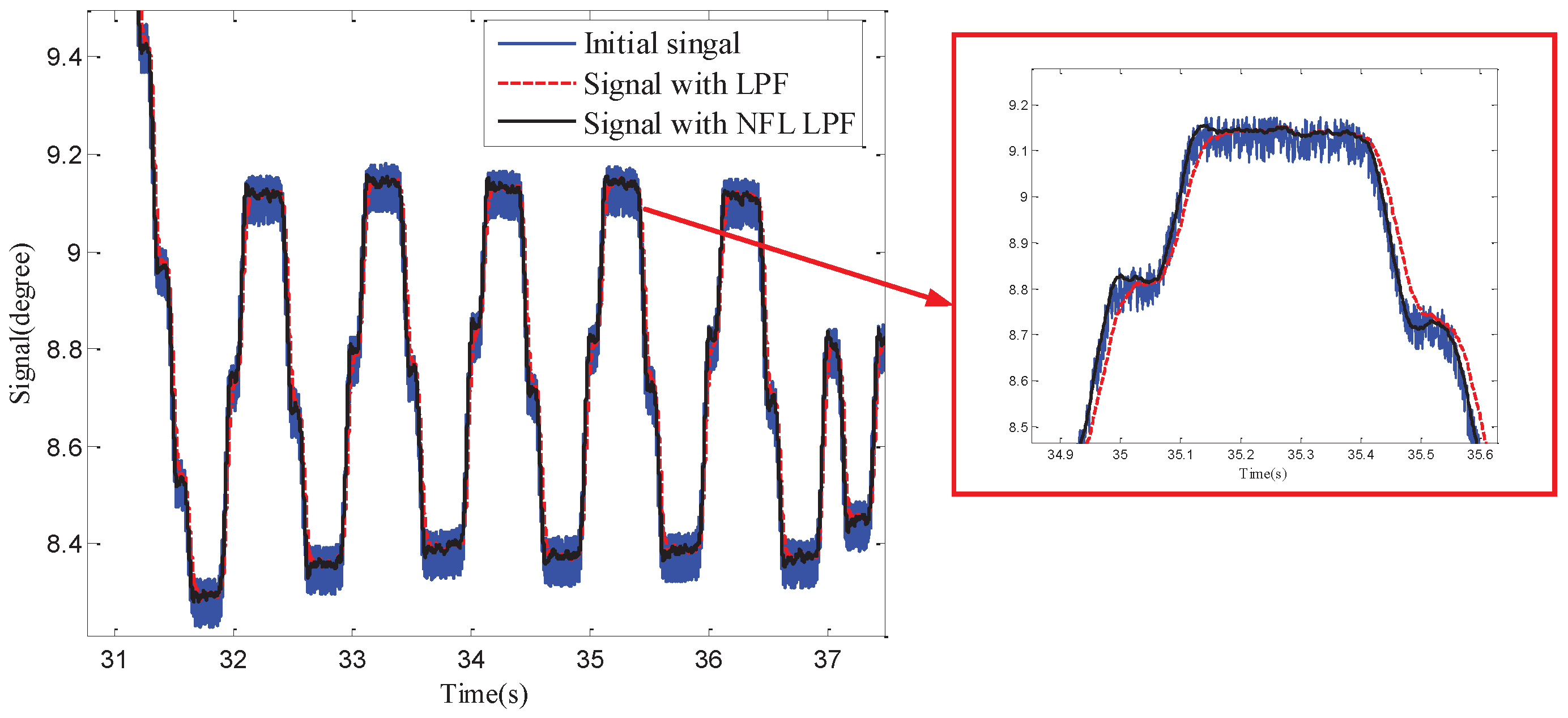
3.2. Phase Lag-Free Sensor Filter
3.3. Disturbance Suppression Control Strategy Based on Non-Singular Terminal Sliding Mode
4. Experimental Results and Discussion
4.1. Implementation of the Experimental System
4.2. Experimental Results and Discussions
4.2.1. Sensor Data Processing
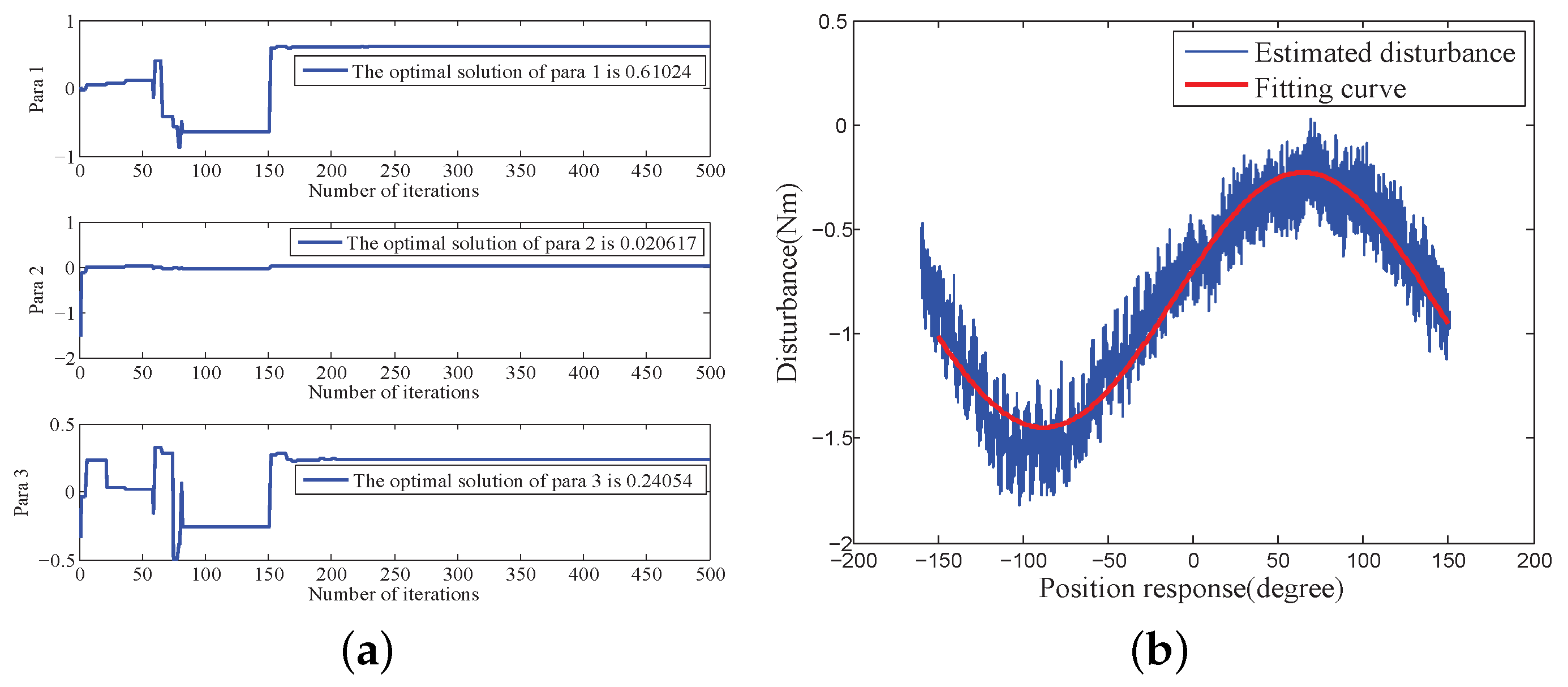
4.2.2. Internal Disturbance Model Identification
4.2.3. Finite-Time Disturbance Observer
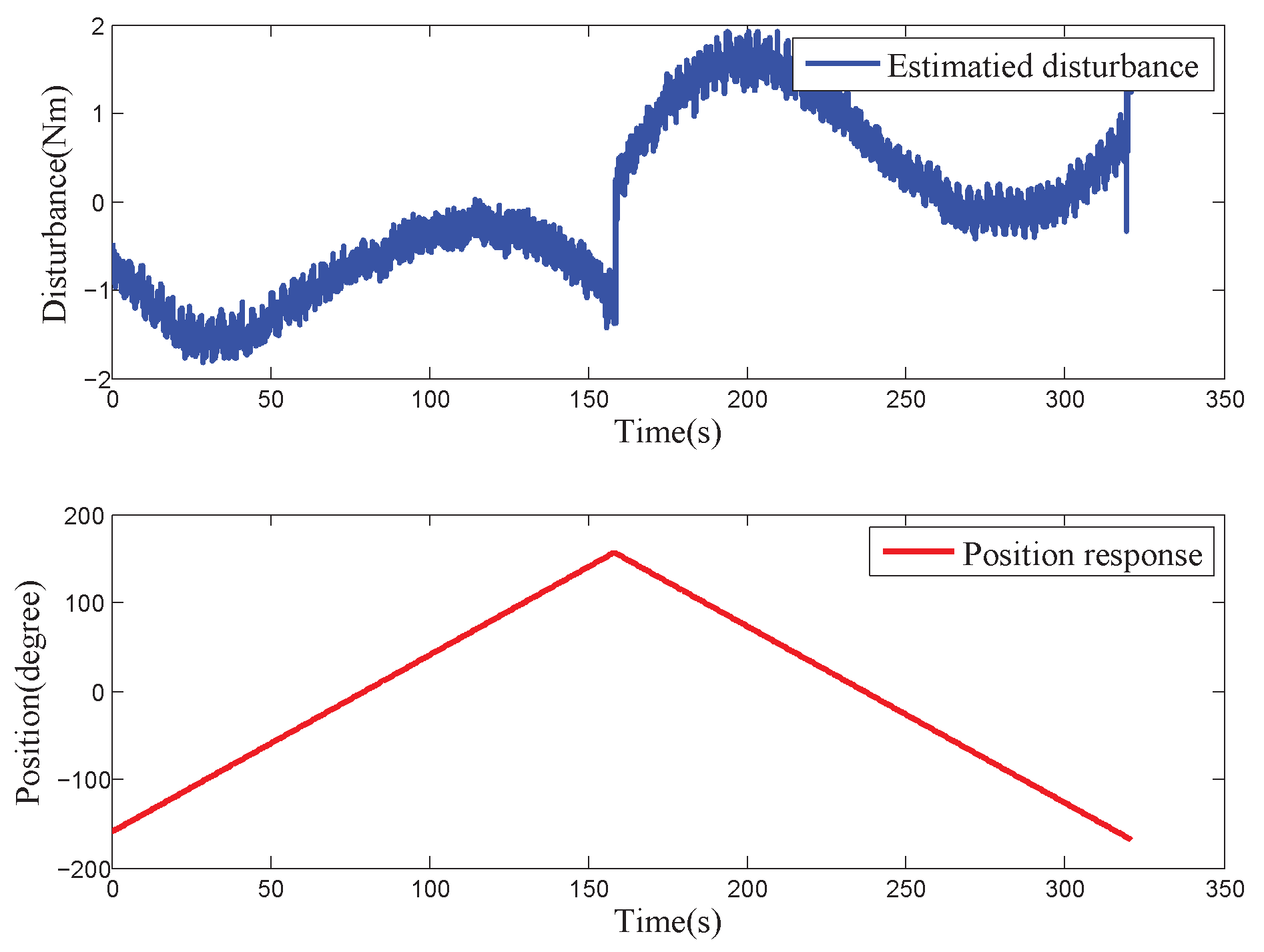
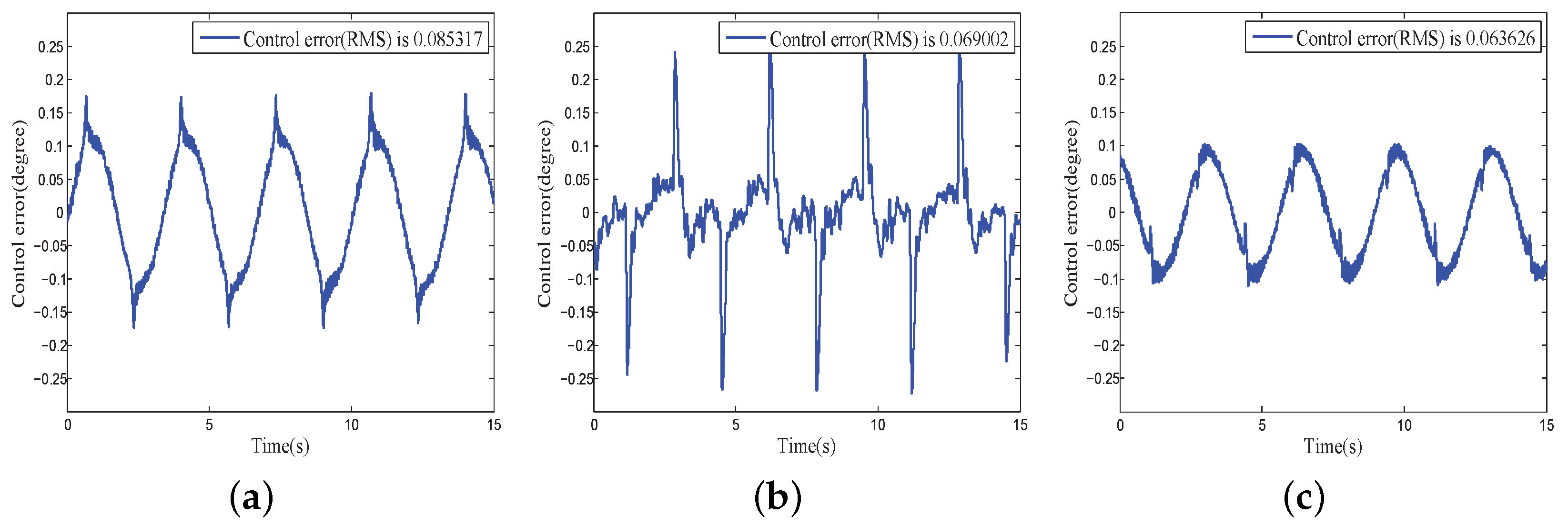
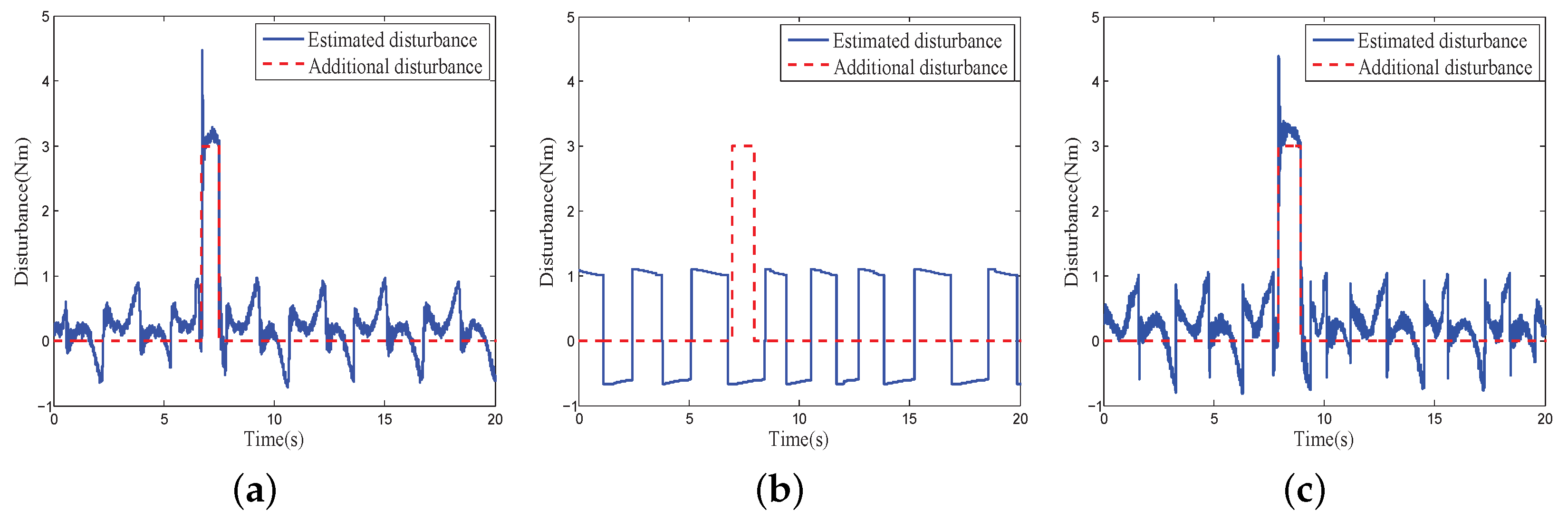
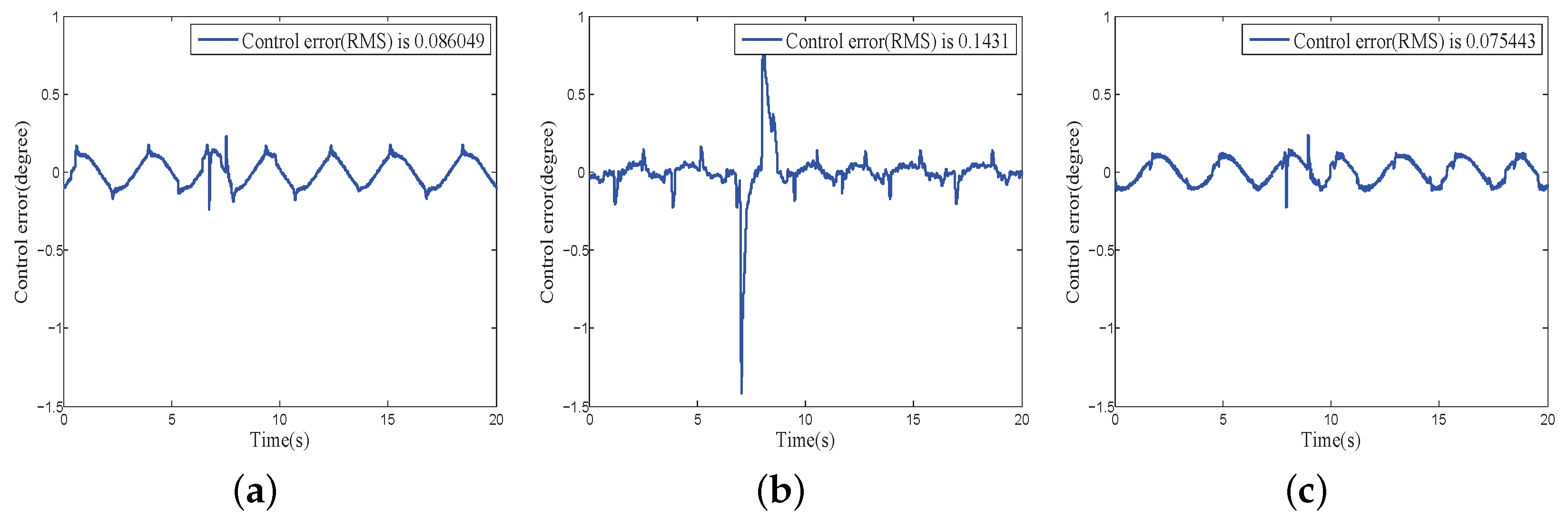
4.2.4. Disturbance Compensation Performance under Multiple Disturbances
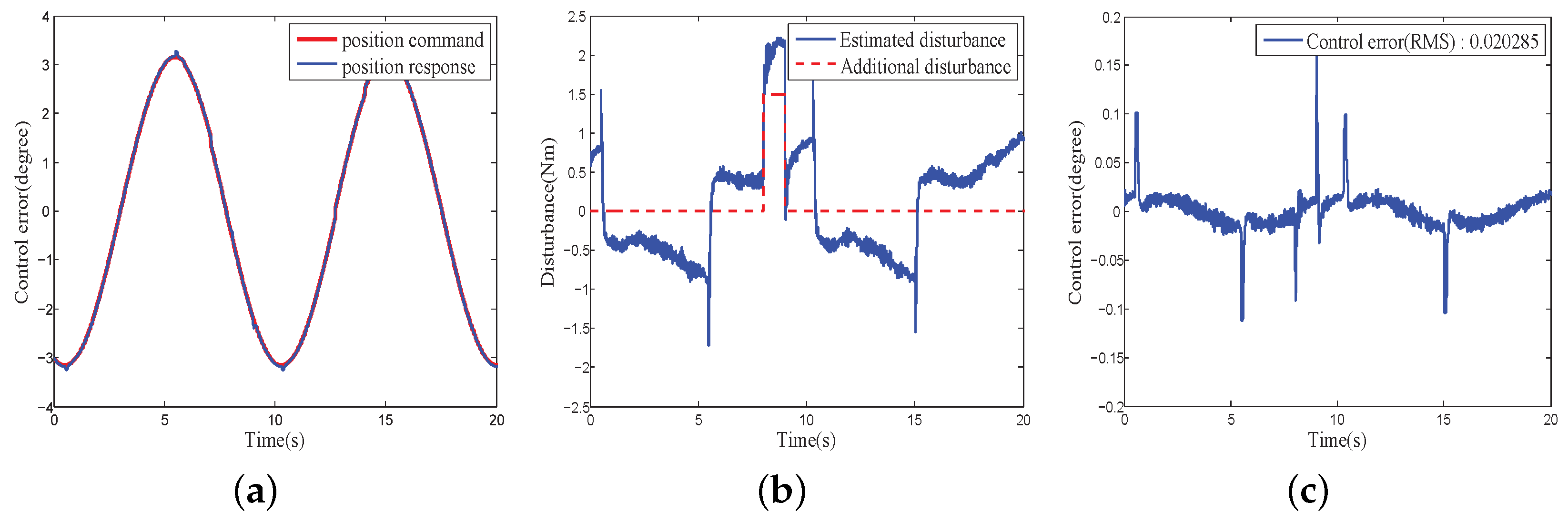
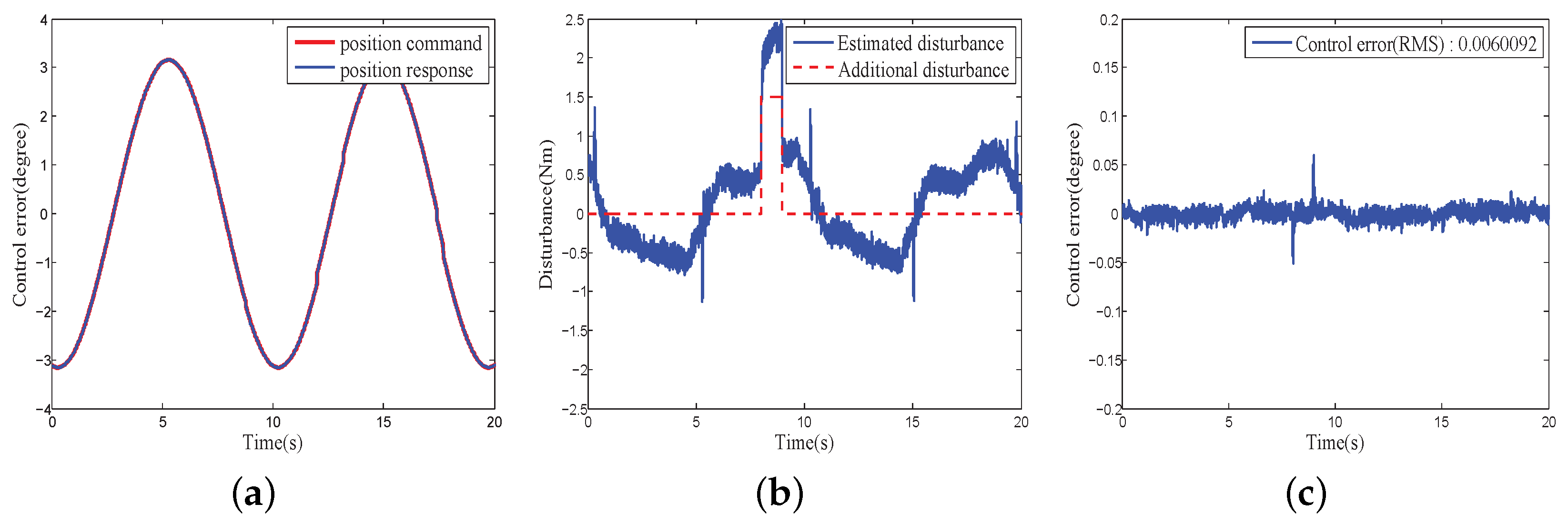
4.2.5. Performance of the Proposed CHADC for COPs
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, Y.; Lin, Z.J.; Liu, F.Z. Stable imaging and accuracy issues of low-altitude unmanned aerial vehicle photogrammetry systems. Remote Sens. 2016, 8, 316. [Google Scholar] [CrossRef]
- Luo, Y.; Huang, Y.M.; Deng, C.; Mao, Y.; Ren, W.; Wu, Q.Y. Combining a disturbance observer with triple-loop control based on MEMS accelerometers for line-of-Sight stabilization. Sensors 2017, 17, 2648. [Google Scholar] [CrossRef] [PubMed]
- Hirwa, S.; Feyel, P.; Duc, G.; Sandou, G. Reduced order controllers for inertial line of sight stabilization. In Proceedings of the 7th IFAC Symposium on Robust Control Design, Aalborg, Denmark, 20–22 June 2012; pp. 103–108. [Google Scholar]
- Abdo, M.M.; Vali, A.R.; Toloei, A.R.; Arvan, M.R. Stabilization loop of a two axes gimbal system using self-tuning PID type fuzzy controller. ISA Trans. 2014, 56, 591–602. [Google Scholar] [CrossRef] [PubMed]
- Xing, H.L.; Jeon, J.H.; Park, K.C.; Oh, I.K. Active disturbance rejection control for precise position tracking of ionic polymer-metal composite actuators. IEEE/ASME Trans. Mechatron. 2013, 18, 86–95. [Google Scholar] [CrossRef]
- Sofla, M.S.; Zareinejad, M.; Parsa, M.; Sheibani, H. Integral based sliding mode stabilizing a camera platform using Kalman filter attitude estimation. Mechatronics 2017, 44, 42–51. [Google Scholar] [CrossRef]
- Toloei, A.R.; Pirzadehb, M.; Valitorques, A.R. Design of predictive control and evaluate the effects of flight dynamics on performance of one axis gimbal system, considering disturbance. Aerosp. Sci. Technol. 2016, 54, 143–150. [Google Scholar] [CrossRef]
- Leroy, E.; Hafez, M. Ultrasonic spherical motor for compact inertially stabilized platforms. In Proceedings of the 2012 International Symposium on Optomechatronic Technologies (ISOT), Paris, France, 29–31 October 2012; pp. 1–5. [Google Scholar]
- Chen, W.H.; Yang, J.; Guo, L.; Li, S.H. Disturbance-Observer-Based Control and Related Methods—An Overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef] [Green Version]
- Xia, Y.Q.; Fu, M.Y.; Deng, Z.H.; Ren, X.M. Recent developments in sliding mode control and active disturbance rejection control. Control Theory Appl. 2013, 30, 137–147. [Google Scholar]
- Babaghasabha, R.; Khosravi, M.A.; Taghirad, H.D. Adaptive robust control of fully-constrained cable driven parallel Robots. Mechatronics 2015, 25, 27–36. [Google Scholar] [CrossRef]
- Mary, A.D.; Mathew, A.T.; Jacob, J. H-infinity disturbance rejection for robust control of tractor trailer systems. Int. Rev. Autom. Control 2012, 5, 262–273. [Google Scholar]
- Ohnishi, K.; Shibata, M.; Murakami, T. Motion control for advanced mechatronics. IEEE/ASME Trans. Mechatron. 1996, 1, 56–67. [Google Scholar] [CrossRef]
- Sariyildiz, E.; Ohnishi, K. Stability and robustness of disturbance-observer-based motion control systems. IEEE Trans. Ind. Electron. 2015, 62, 414–422. [Google Scholar] [CrossRef]
- Han, J.Q.T. From PID to active disturbance rejection control. IEEE Trans. Ind. Eletron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Nowak, P.; Czeczot, J.; Klopot, T. Robust tuning of a first order reduced Active Disturbance Rejection Controller. Control Eng. Pract. 2018, 74, 44–57. [Google Scholar] [CrossRef]
- Chen, W.H.; Ballance, D.J.; Gawthrop, P.J.; O’Reilly, J. A nonlinear disturbance observer for robotic manipulators. IEEE Trans. Ind. Electron. 2000, 47, 932–938. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Li, S.; Sun, C.; Guo, L. Nonlinear-Disturbance-Observer-Based Robust Flight Control for Airbreathing Hypersonic Vehicles. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1263–1275. [Google Scholar] [CrossRef]
- She, J.H.; Xin, X.; Ohyama, Y. Estimation of equivalent input disturbance improves vehicular steering control. IEEE Trans. Veh. Technol. 2007, 56, 3722–3731. [Google Scholar] [CrossRef]
- Liu, R.J.; Wy, M.; Liu, G.P.; She, J.H.; Thomas, C. Active disturbance rejection control based on an improved equivalent-input-disturbance approach. IEEE/ASME Trans. Mechatron. 2013, 18, 1410–1413. [Google Scholar] [CrossRef]
- Jamaludin, Z.; Brussel, H.V.; Swevers, J. Friction compensation of an XY teed table using friction-model-based reedforward and an inverse-model-based disturbance observer. IEEE Trans. Ind. Electron. 2009, 56, 3848–3853. [Google Scholar] [CrossRef]
- Cong, S.; Deng, K.; Shang, W.W.; Kong, D.J.; Shen, H.H. Isolation control for inertially stabilized platform based on nonlinear friction compensation. Nonlinear Dyn. 2016, 84, 1123–1133. [Google Scholar] [CrossRef]
- Chen, X.D.; Fang, F.; Luo, X. A friction identification approach based on dual-relay feedback configuration with application to an inertially stabilized platform. Mechatronics 2014, 24, 1120–1131. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Zhao, B.L.; Liu, W.; Yue, H.X.; Yu, R.X.; Zhao, Y.L. A compound scheme on parameters identification and adaptive compensation of nonlinear friction disturbance for the aerial inertially stabilized platform. ISA Trans. 2017, 67, 293–305. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Zhou, X.Y. Nonlinear friction modeling and adaptive compensation on an inertially stabilized platform system for aerial remote sensing application. J. Mech. Eng. 2013, 49, 122–129. [Google Scholar] [CrossRef]
- Mitra, R.; Sozer, Y. Torque ripple minimization of switched reluctance motors through speed signal processing. Energy Convers. Congr. Expos. 2014, 1366–1373. [Google Scholar]
- Li, M.; Li, J.; Zhang, Y.S. modeling and simulation of imbalance disturbance for inertially stabilized platforms. J. Vib. Shock 2016, 35, 138–153. [Google Scholar]
- Su, K.H.; Cheng, M.Y.; Chang, Y.C. Contouring accuracy improvement of parametric free-form curves—A Fuzzy Logic-based Disturbance Compensation approach. IEEE Int. Conf. Mechatron. 2013, 6, 730–735. [Google Scholar]
- Herrmann, G.; Lewis, F.L.; Ge, S.S.; Zhang, J. Discrete adaptive neural network disturbance feedforward compensation for non-linear disturbances in servo-control applications. Int. J. Control 2009, 82, 721–740. [Google Scholar] [CrossRef]
- Guo, L. Composite hierarchical anti-disturbance control(CHADC) for system with multiple disturbances: Survey and overview. In Proceedings of the 30th Chinese Control Conference, Yantai, China, 22–24 July 2011; pp. 6193–6198. [Google Scholar]
- Aboudonia, A.; Rashad, R.; El-Badawy, A. Composite hierarchical anti-disturbance control of a quadrotor UAV in the presence of matched and mismatched disturbances. J. Intell. Robot. Syst. 2018, 90, 201–216. [Google Scholar] [CrossRef]
- Peng, C.; Fang, J.; Xu, S. Composite anti-disturbance controller for magnetically suspended control moment gyro subject to mismatched disturbances. Nonlinear Dyn. 2015, 79, 1563–1573. [Google Scholar] [CrossRef]
- Foti, F.; Martinelli, L. Mechanical modeling of metallic strands subjected to tension, torsion and bending. Int. J. Solids Struct. 2016, 91, 1–17. [Google Scholar] [CrossRef]
- Xiang, L.; Wang, H.Y.; Chen, Y.; Guan, Y.J.; Wang, Y.L.; Dai, L.H. Modeling of multi-strand wire ropes subjected to axial tension and torsion loads. Int. J. Solids Struct. 2015, 58, 233–245. [Google Scholar] [CrossRef]
- Xiong, L.W.; Chen, M.F.; Wang, X.; Xu, B.G. System identification method for Hammerstein model based on improved differential evolution algorithm. J. Nanjing Univ. Sci. Technol. 2013, 37, 538–542. [Google Scholar]
- Kim, B.K.; Chung, W.K. Advanced disturbance observer design for mechanical positioning systems. IEEE Trans. Ind. Electron. 2003, 50, 1207–1216. [Google Scholar]
- Li, S.H.; Ding, S.H.; Du, H.B.; Qian, C.J. Theory and Application of Non Smooth Control; Science Press: Beijing, China, 2013; pp. 5–30. [Google Scholar]
- Tian, D.P.; Gao, H.J. Phase-lag-free Low pass filter with higher-order sensors and its application in motion control. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 607–612. [Google Scholar]
- Li, S.H.; Zhou, M.M.; Yu, X.H. Design and Implementation of Terminal Sliding Mode Control Method for PMSM Speed Regulation System. IEEE Trans. Ind. Inform. 2013, 9, 1879–1891. [Google Scholar] [CrossRef]
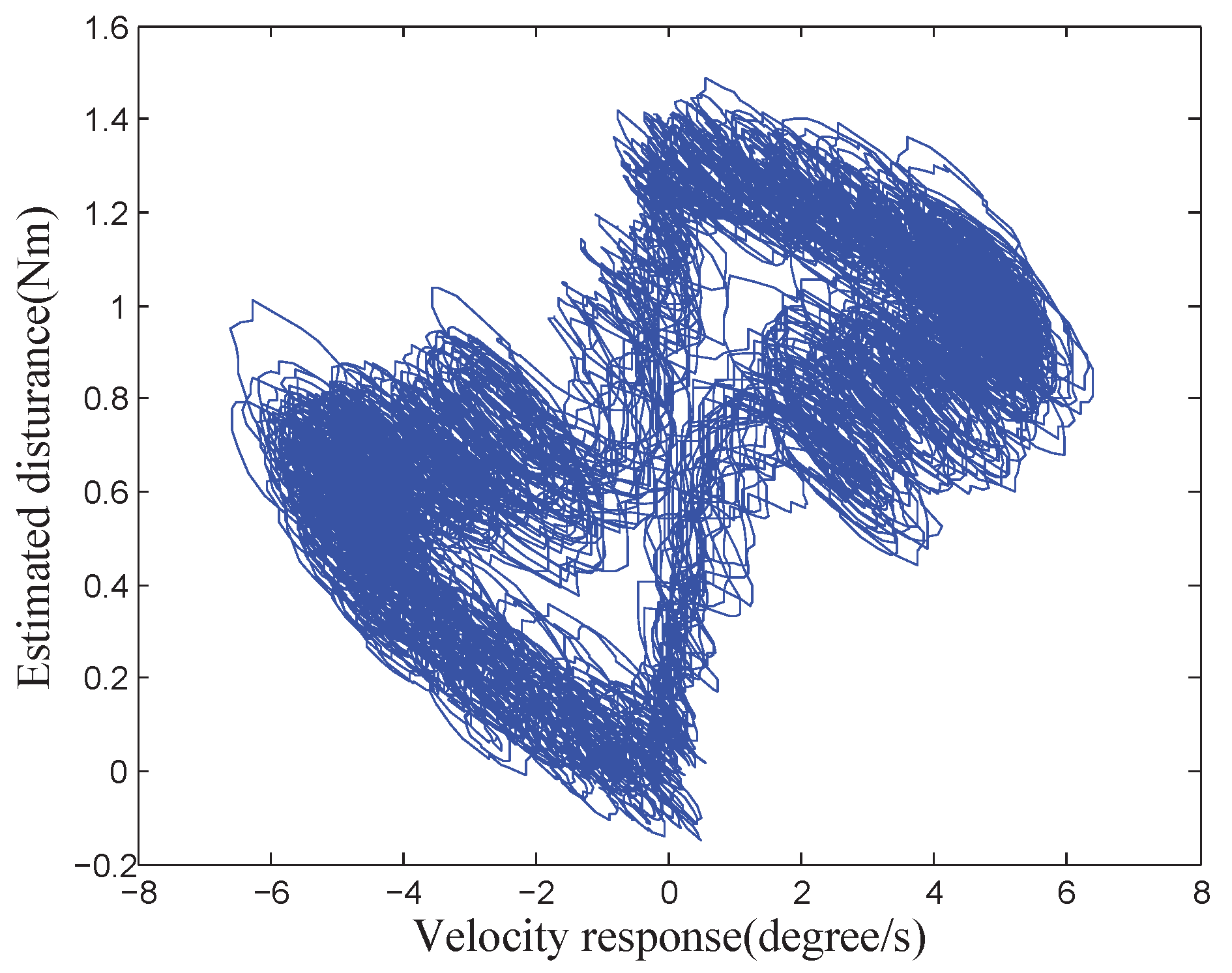





| Parameters | Symbols | Values |
|---|---|---|
| Nominal mass | 0.0021667 [kg m2] | |
| Nominal damping | 0.15 [N s/m] | |
| Filter cutoff frequency | 50 [rad/s] | |
| Nonlinear parameter of finite-time DOB | 0.9 | |
| Amplitude output limit | 8.5 [V] | |
| Cutoff frequency of sensor filter | g | 62.8 [rad/s] |
| Proportional gain of PID | 4 | |
| Integral gain of PID | 8 | |
| Derivative gain of PID | 0.04 | |
| Switching gain of NTSM | l | 400 |
| Control parameter of NTSM | 60 | |
| Non-singular parameter of NTSM | 5/3 |
| Parameters | Symbols | Values |
|---|---|---|
| Number of Decision Variables | 3 | |
| Population Size | 30 | |
| Crossover Probability | ||
| Basic mutation factor | ||
| Maximum number of iterations | 500 | |
| Bound of Scaling Factor 1 | ||
| Bound of Scaling Factor 2 | ||
| Bound of Scaling Factor 3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Tian, D.; Dai, M. Composite Hierarchical Anti-Disturbance Control with Multisensor Fusion for Compact Optoelectronic Platforms. Sensors 2018, 18, 3190. https://doi.org/10.3390/s18103190
Wang Y, Tian D, Dai M. Composite Hierarchical Anti-Disturbance Control with Multisensor Fusion for Compact Optoelectronic Platforms. Sensors. 2018; 18(10):3190. https://doi.org/10.3390/s18103190
Chicago/Turabian StyleWang, Yutang, Dapeng Tian, and Ming Dai. 2018. "Composite Hierarchical Anti-Disturbance Control with Multisensor Fusion for Compact Optoelectronic Platforms" Sensors 18, no. 10: 3190. https://doi.org/10.3390/s18103190
APA StyleWang, Y., Tian, D., & Dai, M. (2018). Composite Hierarchical Anti-Disturbance Control with Multisensor Fusion for Compact Optoelectronic Platforms. Sensors, 18(10), 3190. https://doi.org/10.3390/s18103190






