Reconstructed Order Analysis-Based Vibration Monitoring under Variable Rotation Speed by Using Multiple Blade Tip-Timing Sensors
Abstract
:1. Introduction
2. Angular Sampling-Based BTT Vibration Monitoring under Variable Rotation Speed
2.1. Basic Principles of BTT-Based Vibration Monitoring
2.2. Problem Statements of BTT Vibration Reconstruction under VRS
2.3. Basic Structure of Angular Sampling-Based BTT Vibration Monitoring under VRS
3. Angular-Domain BTT Vibration Reconstruction Algorithms under VRS
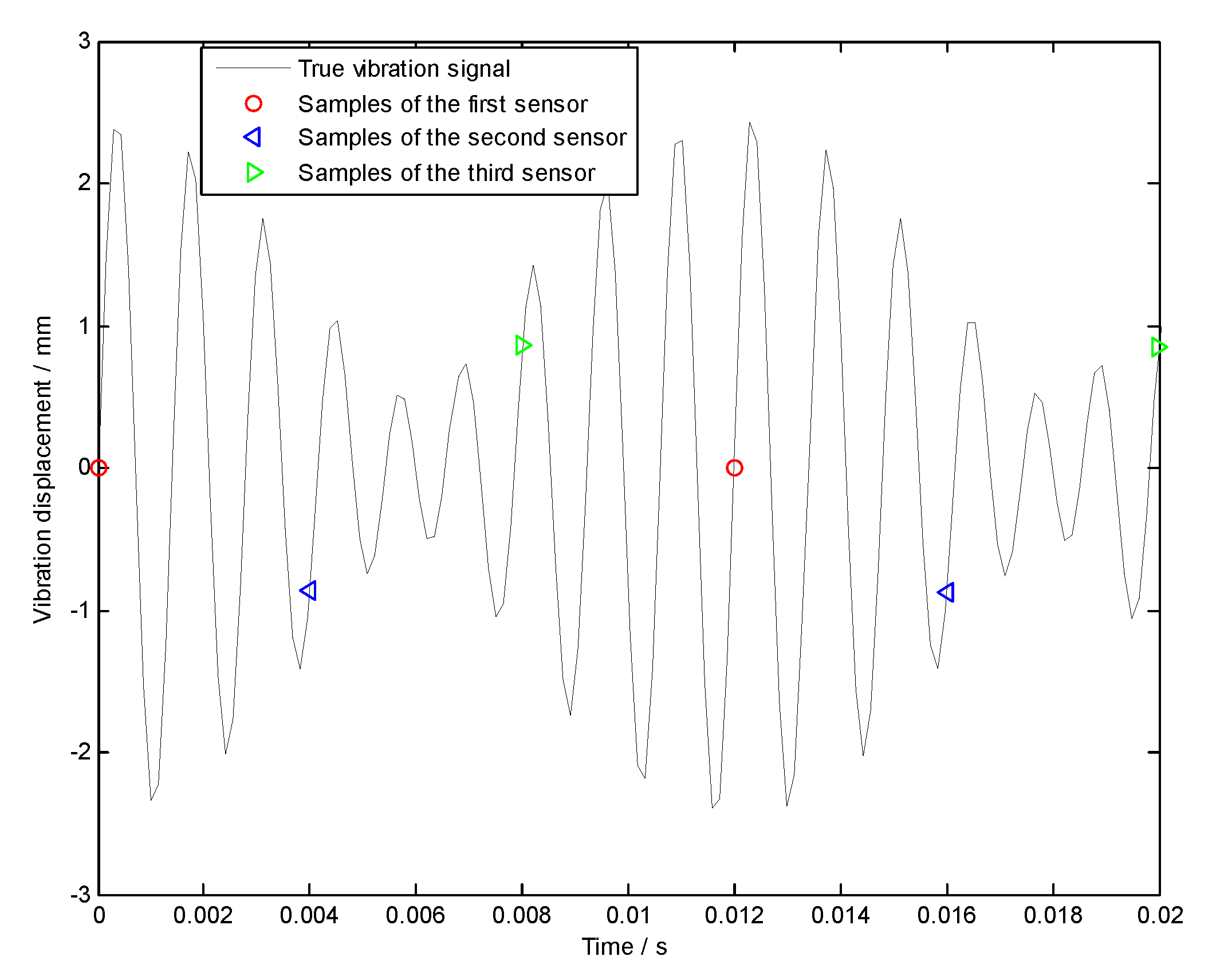
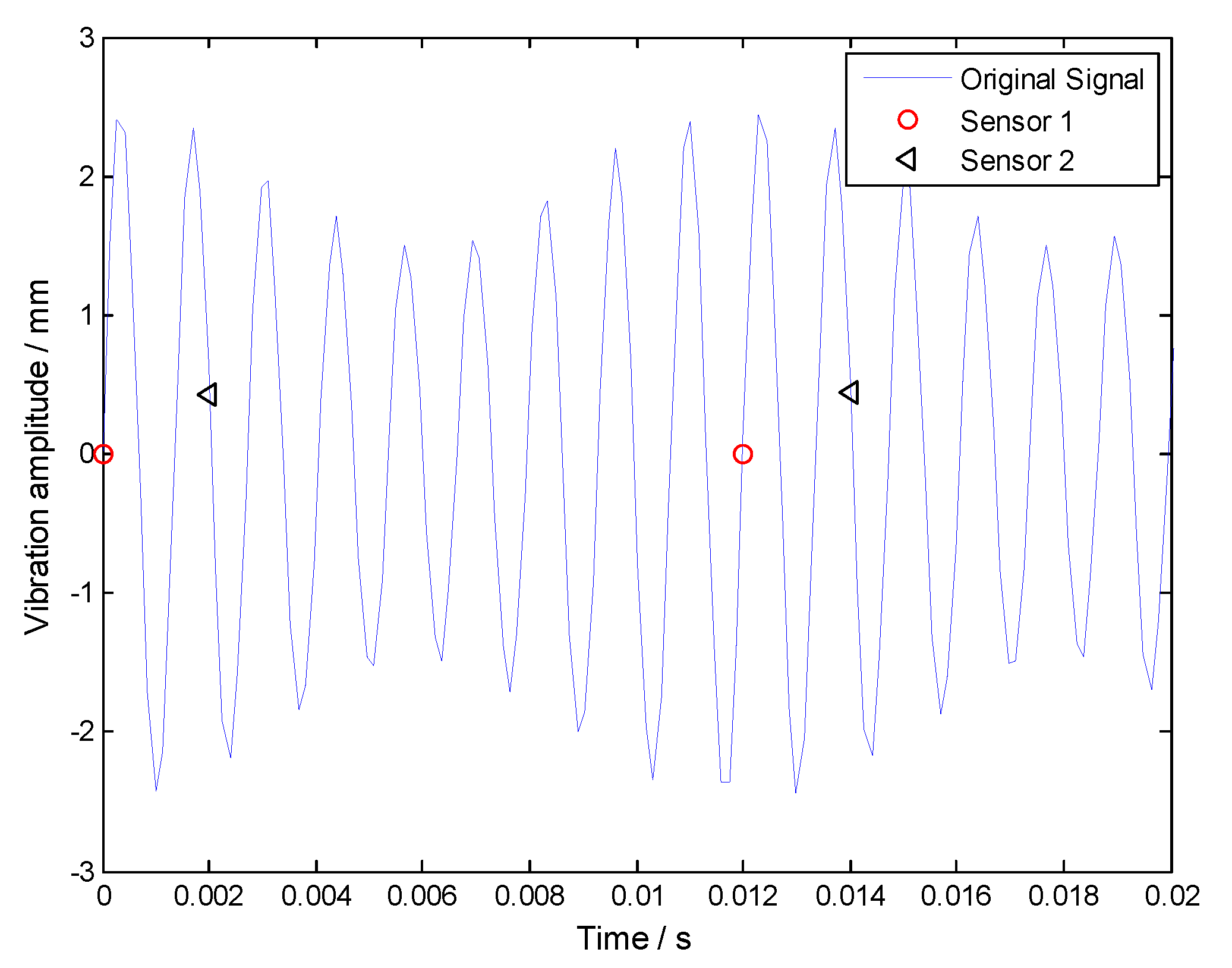
3.1. Uniform BTT Sensor Configuration
3.2. Non-Uniform BTT Sensor Configuration
4. Numerical Simulations and Validations
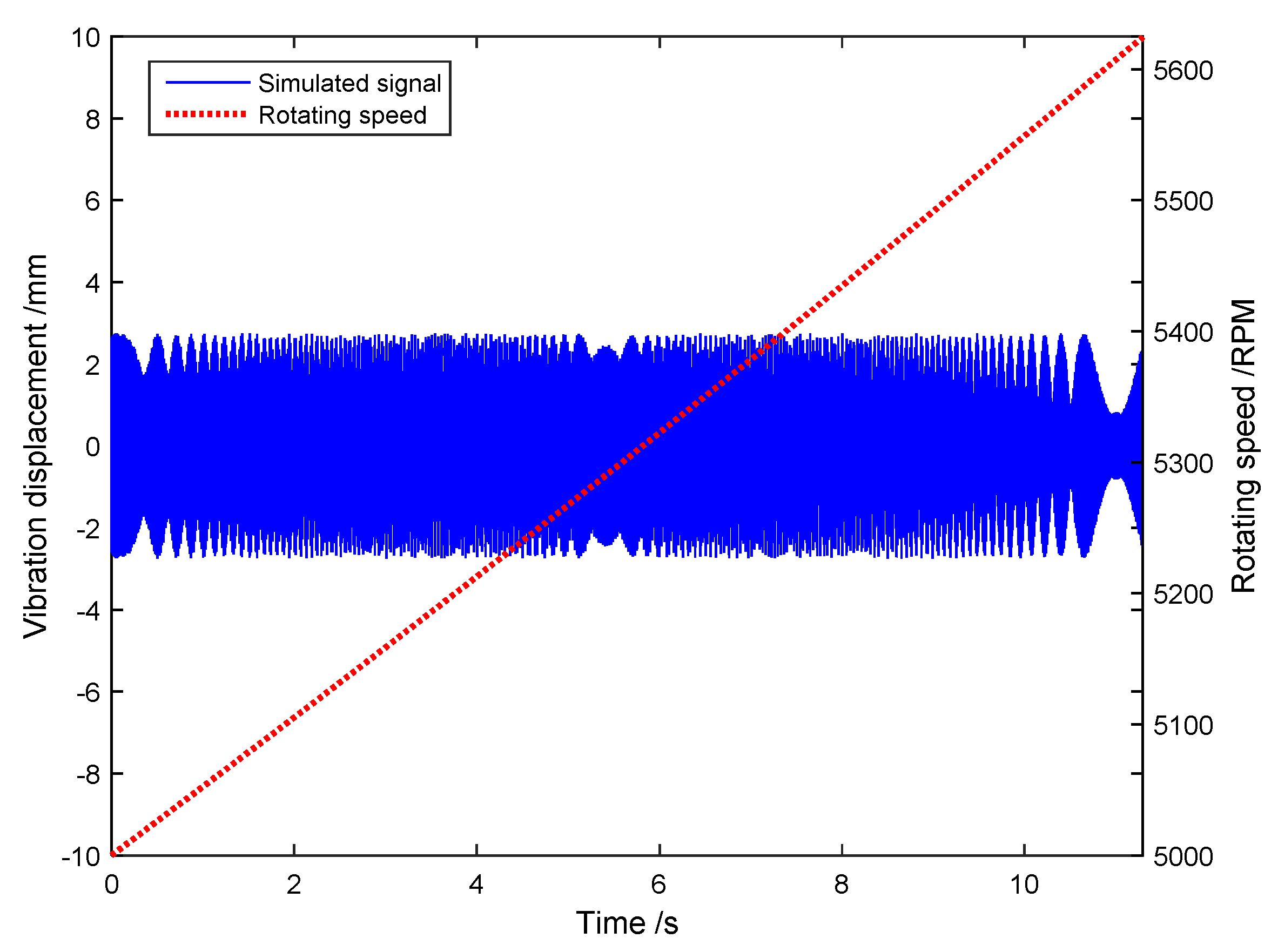
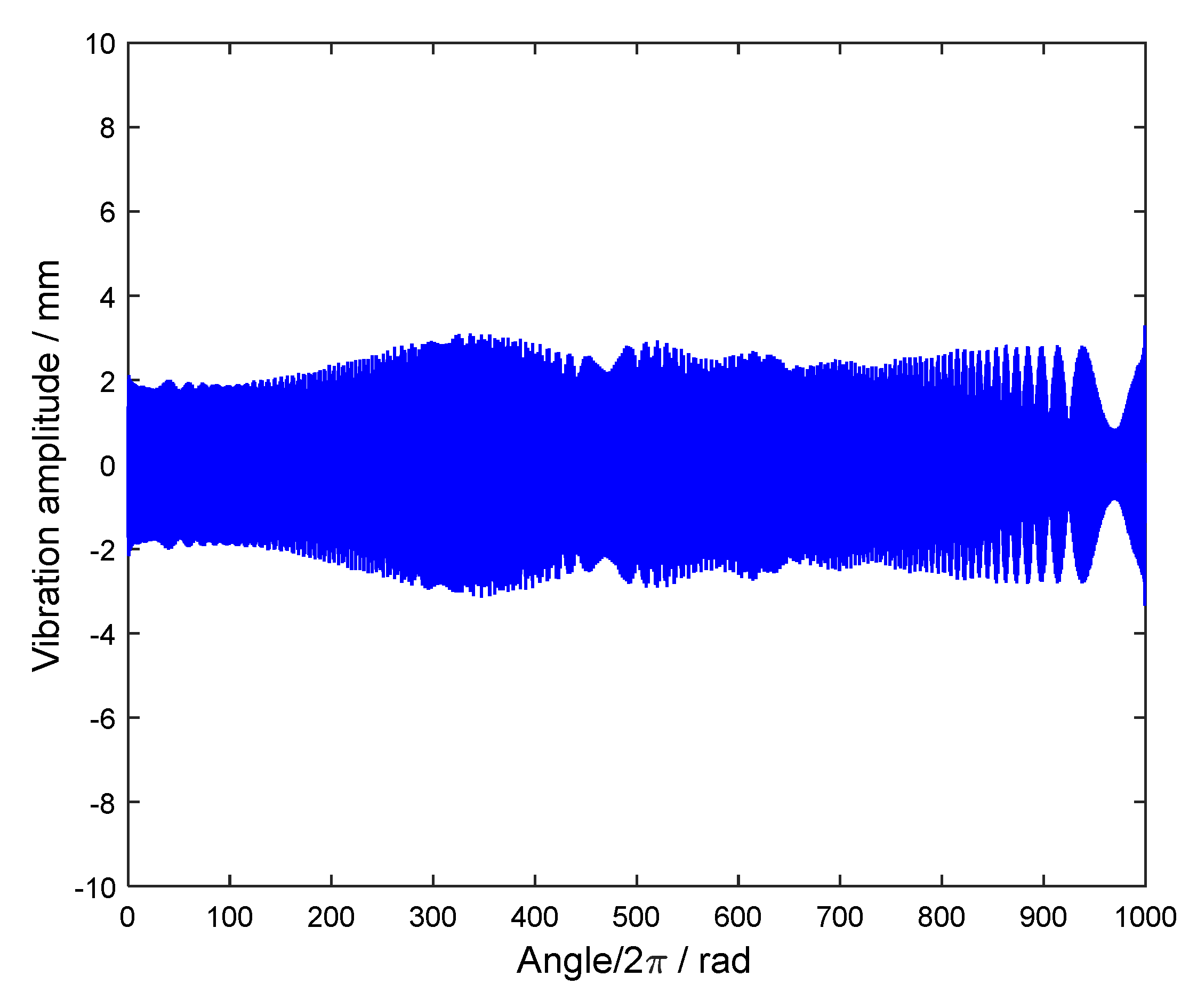
4.1. Simulated Vibration Signals with Variable Frequencies
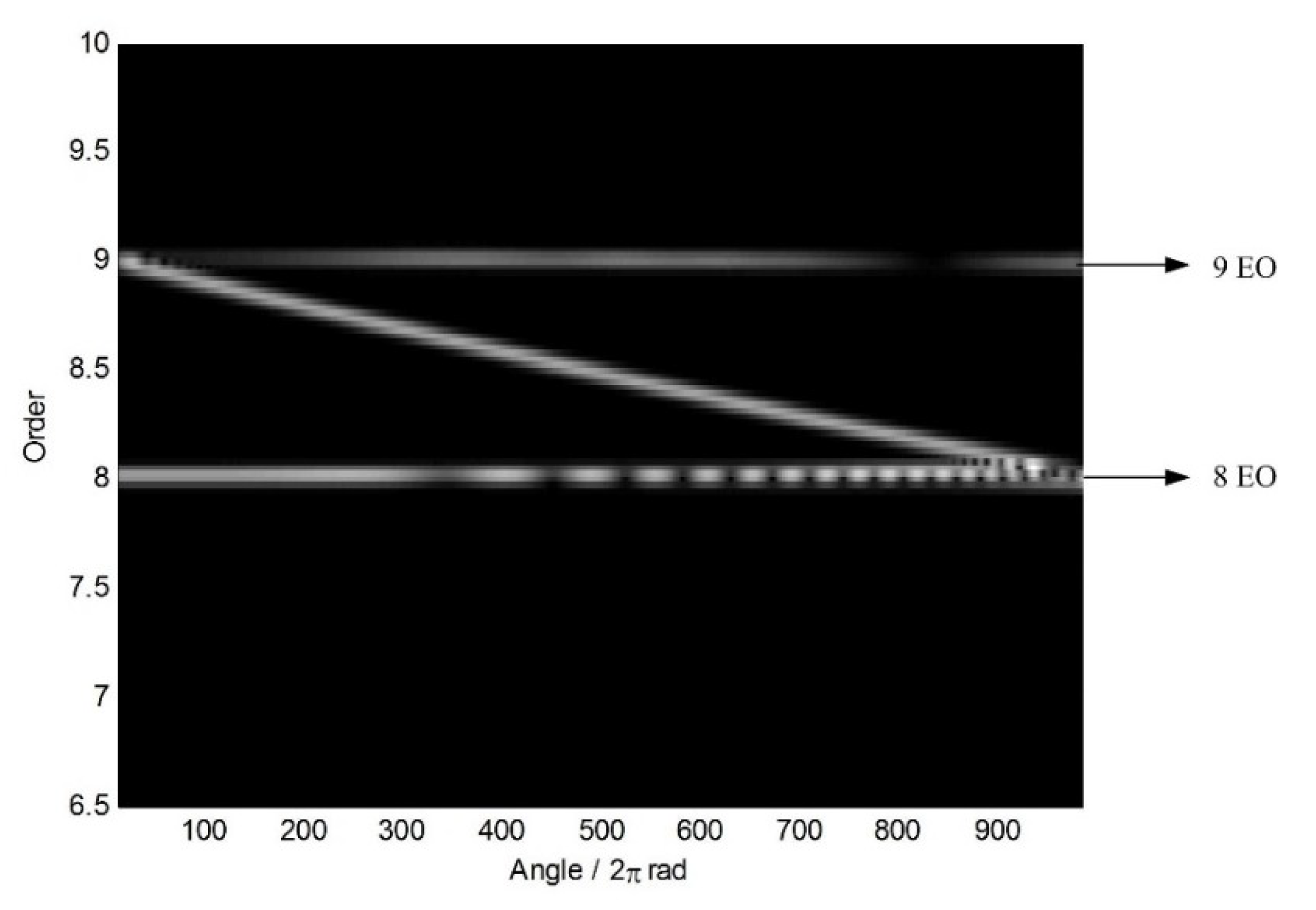
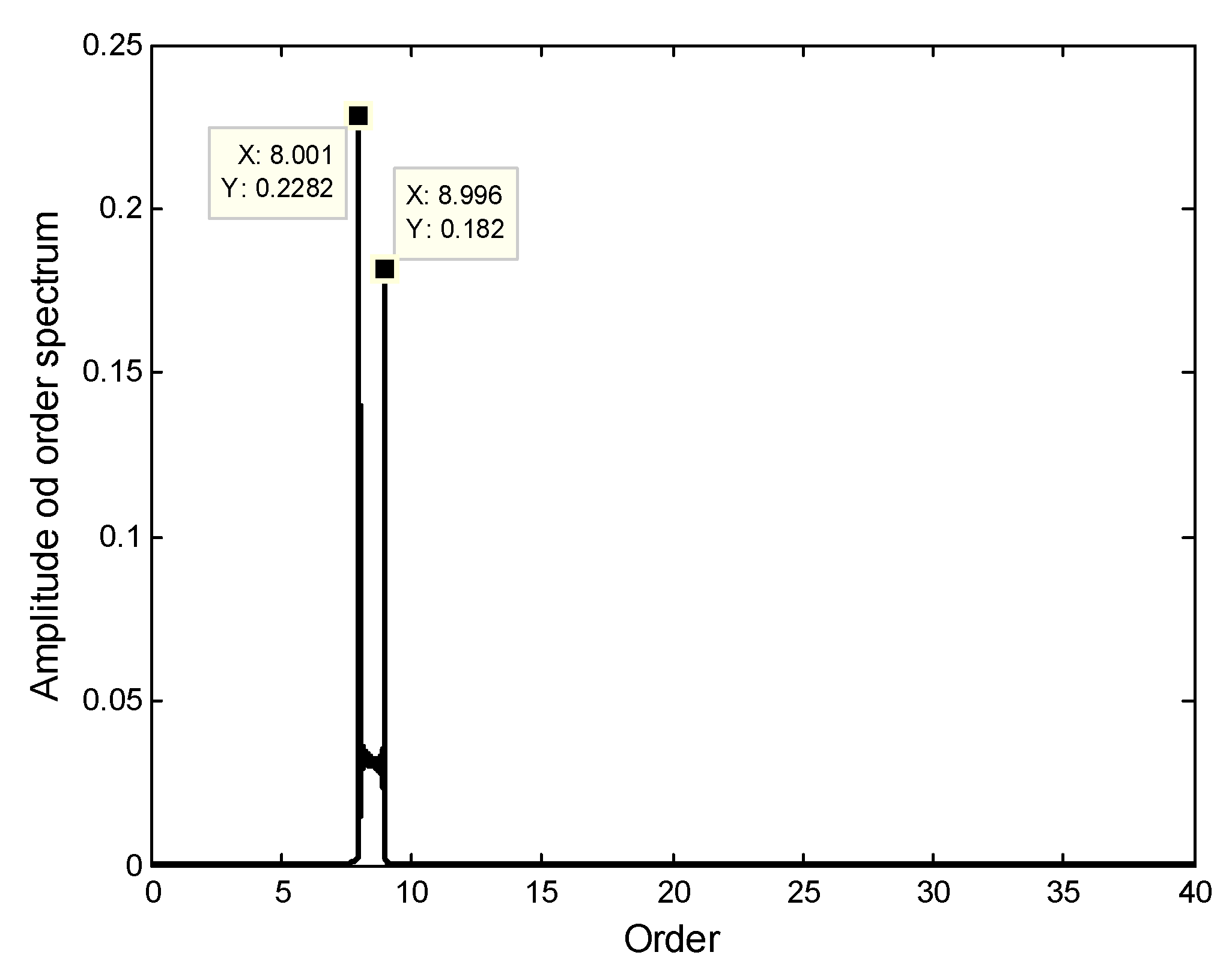
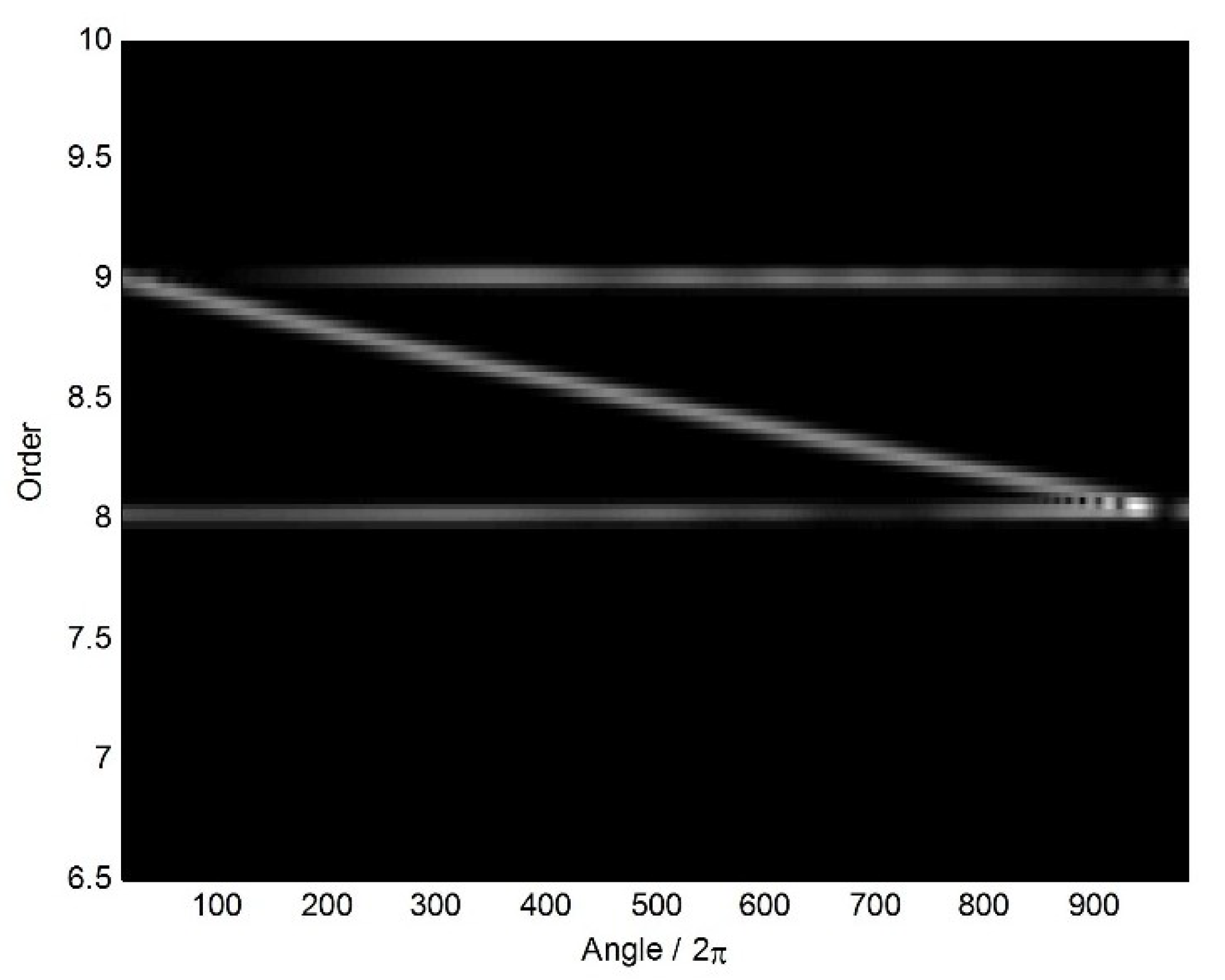
4.2. Reconstruction Results under Uniform BTT Sensor Configuration
4.3. Reconstruction Results under Non-Uniform BTT Sensor Configuration
5. Experimental Validations
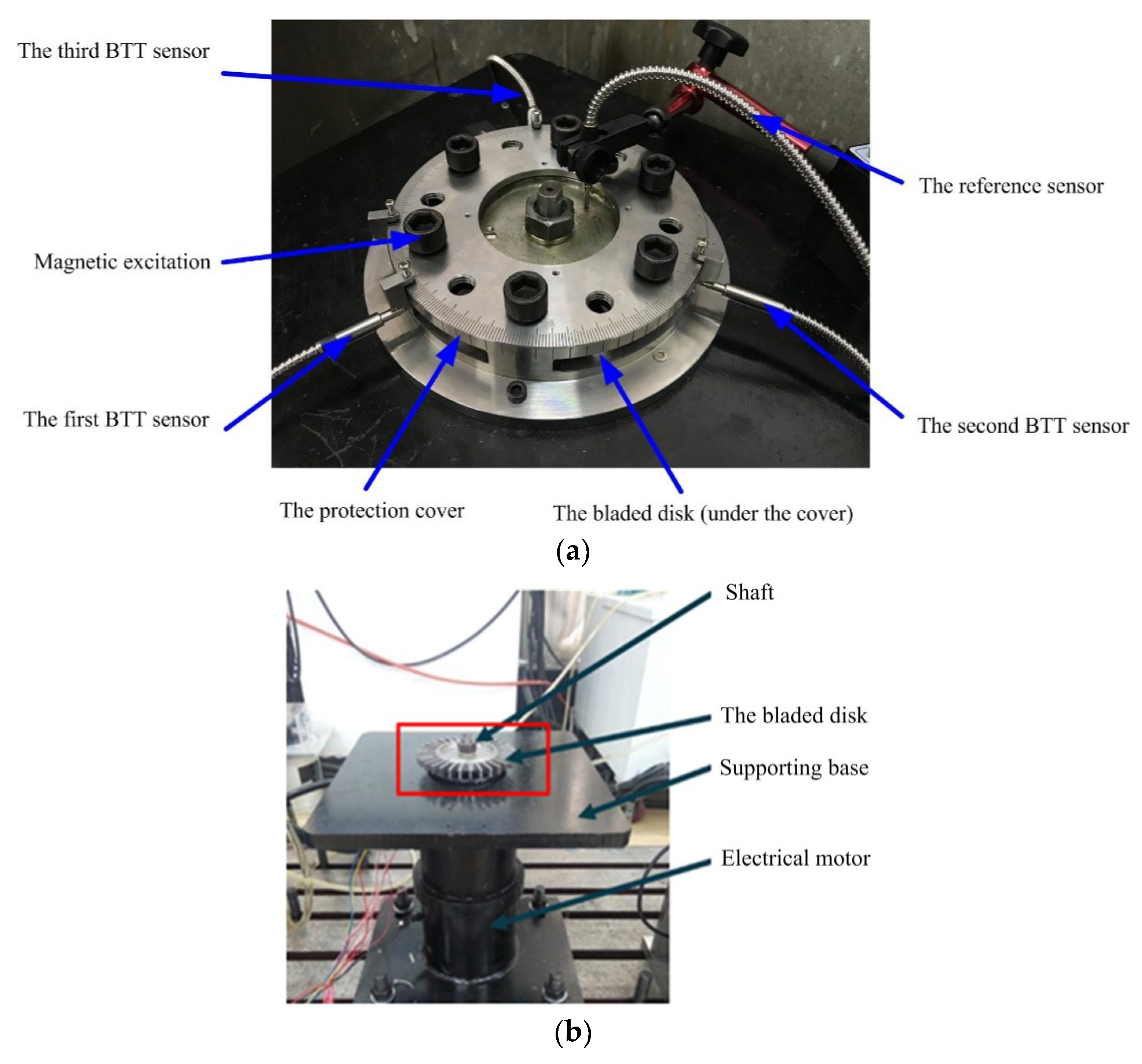
5.1. Experimental Set-Up
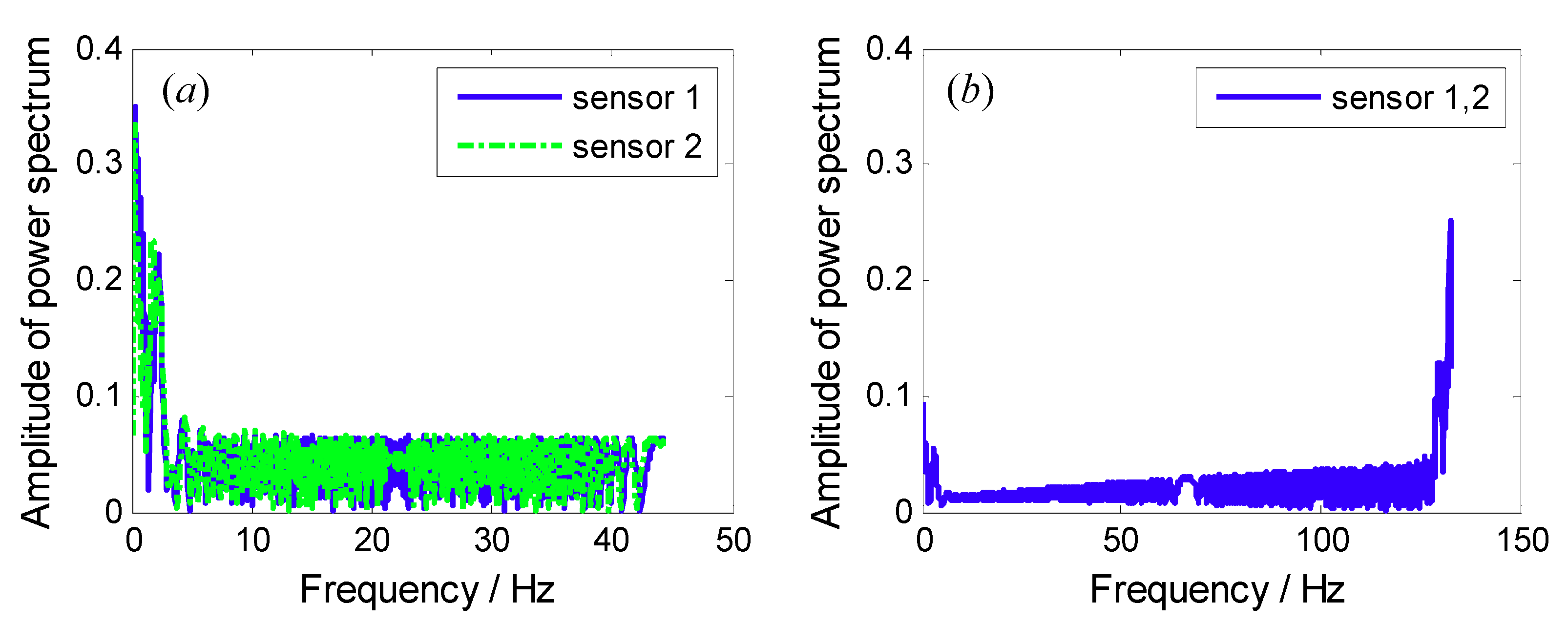
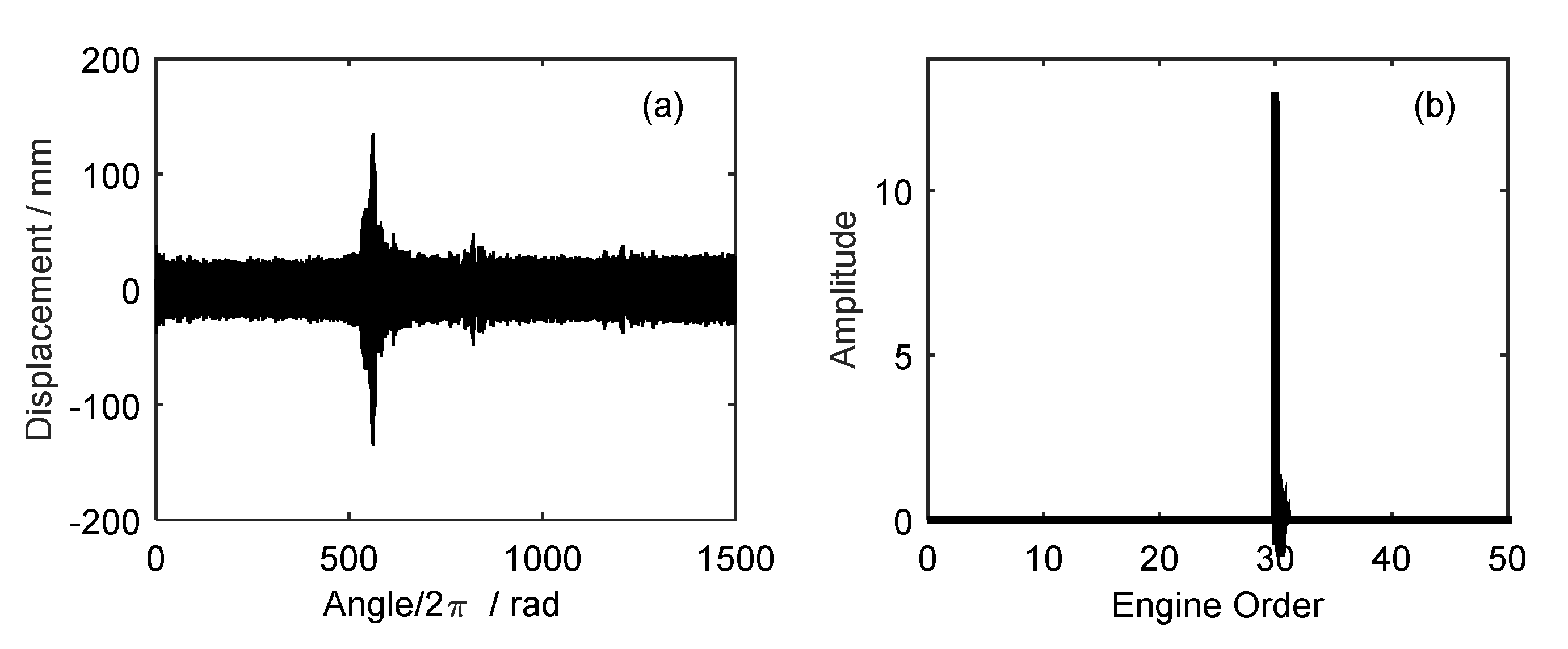
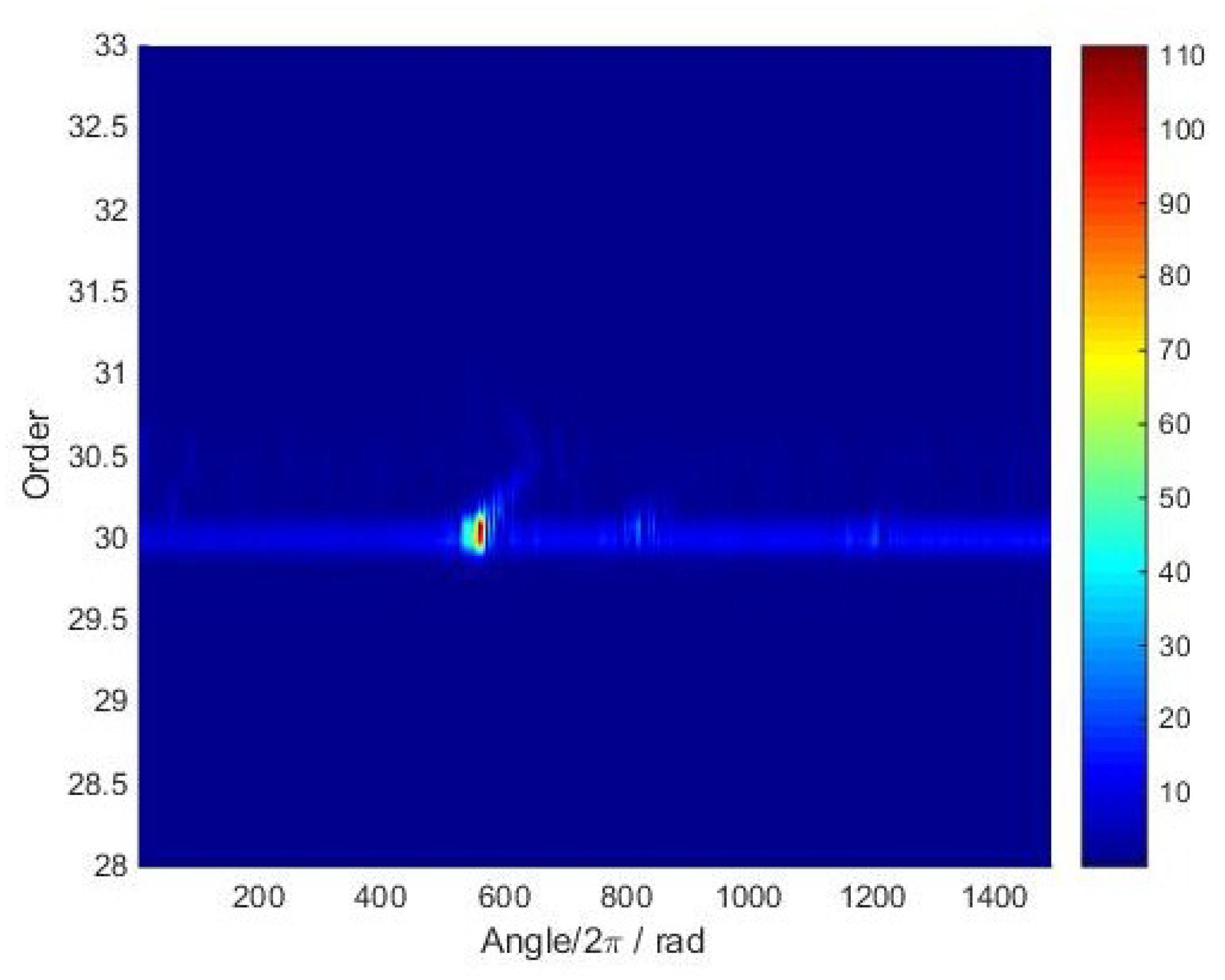
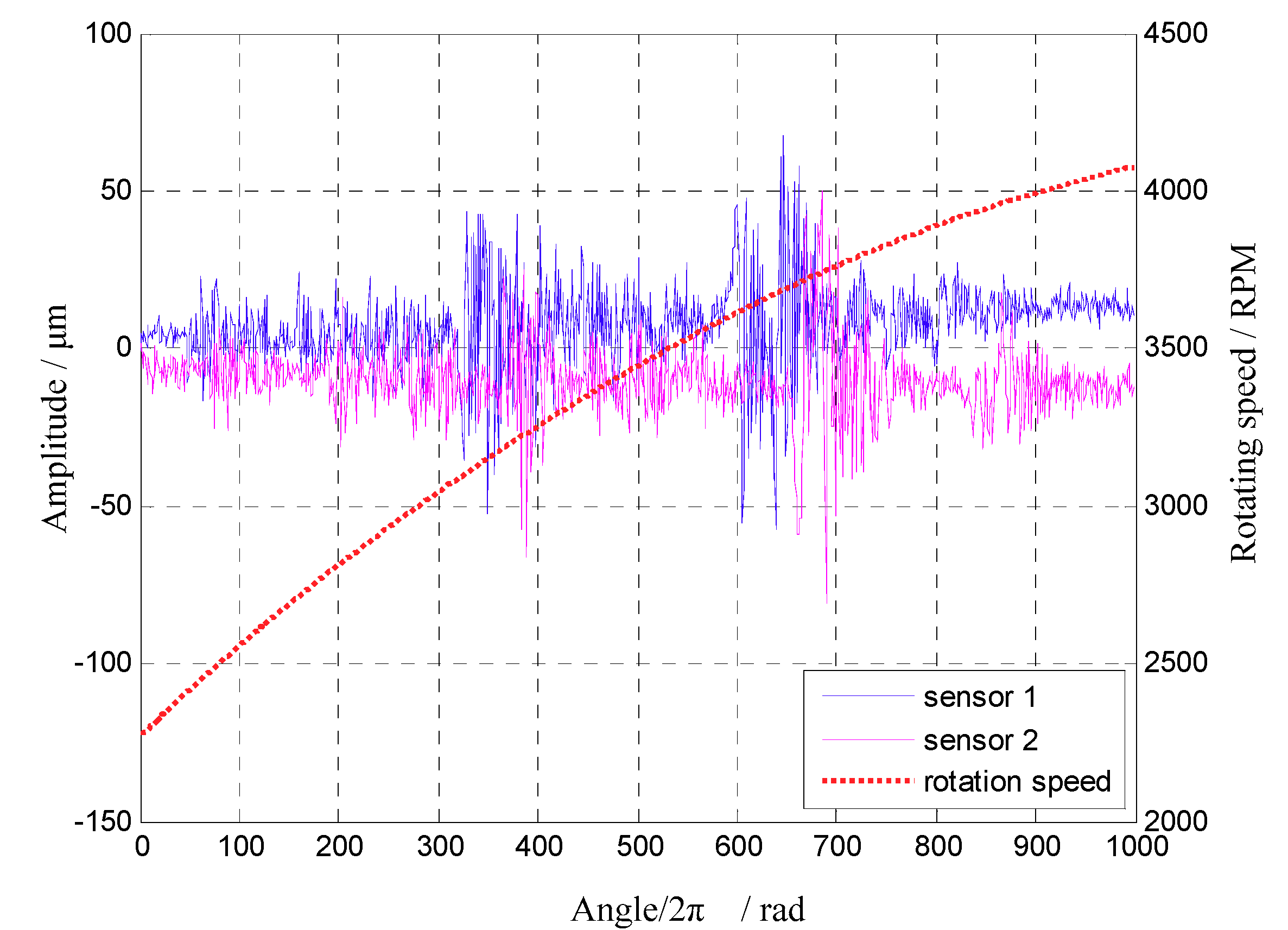
5.2. Experimental Results under Uniform Sensor Configuration
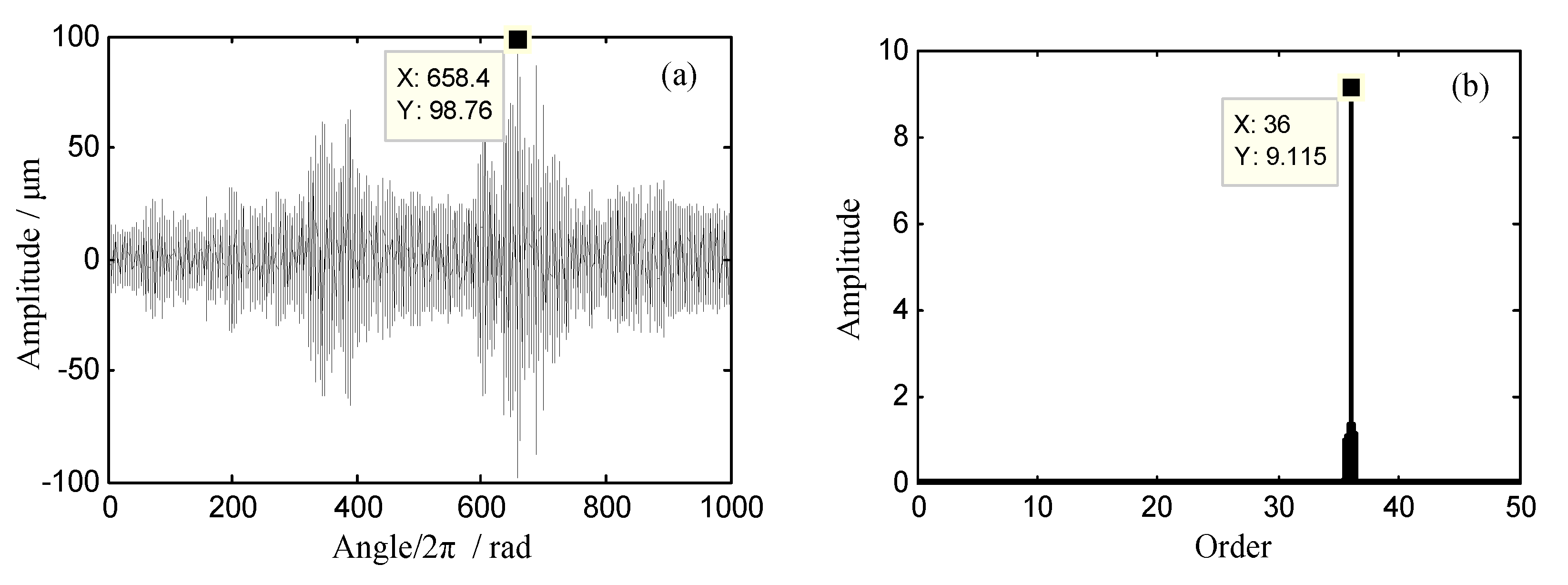
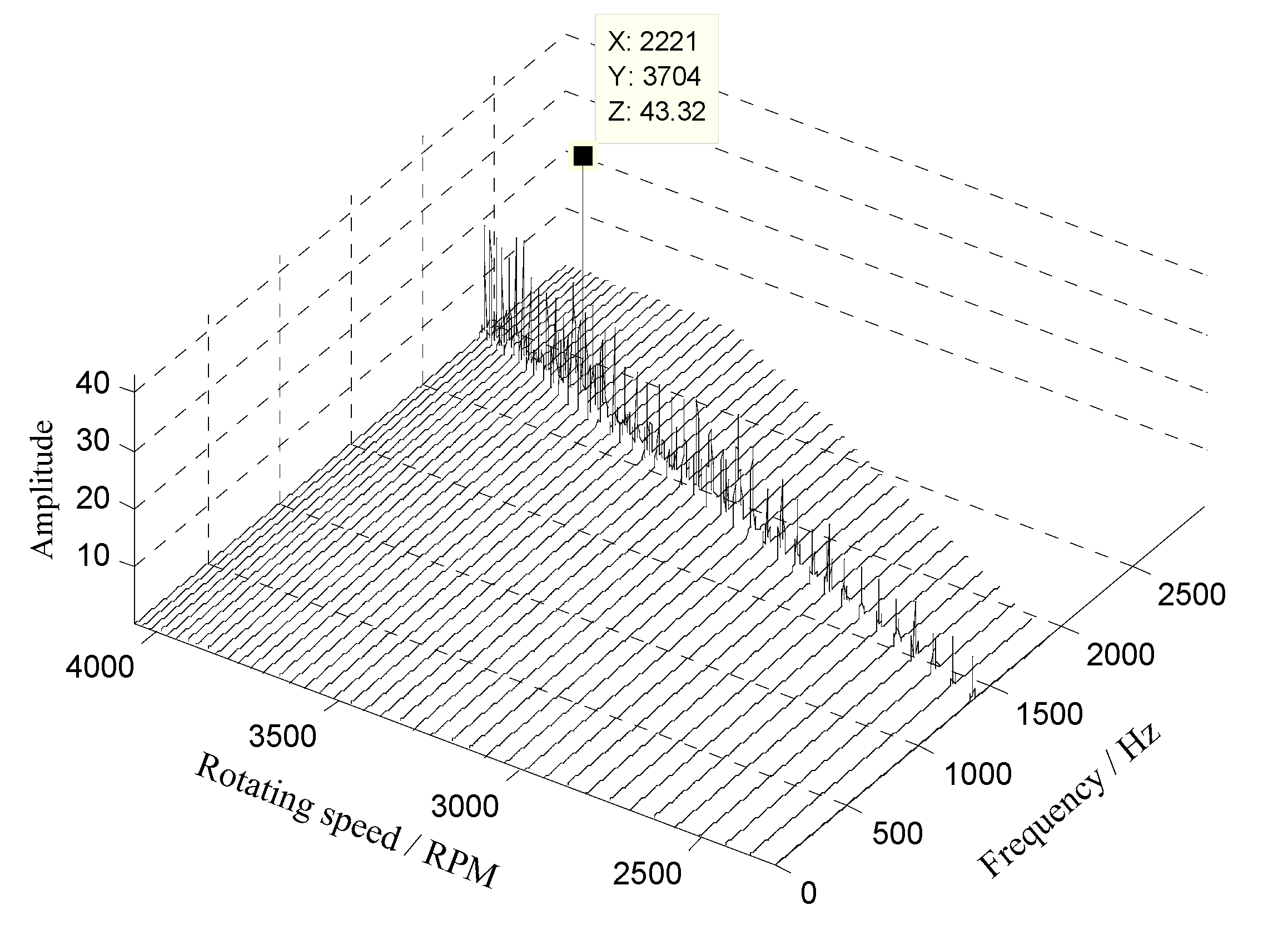
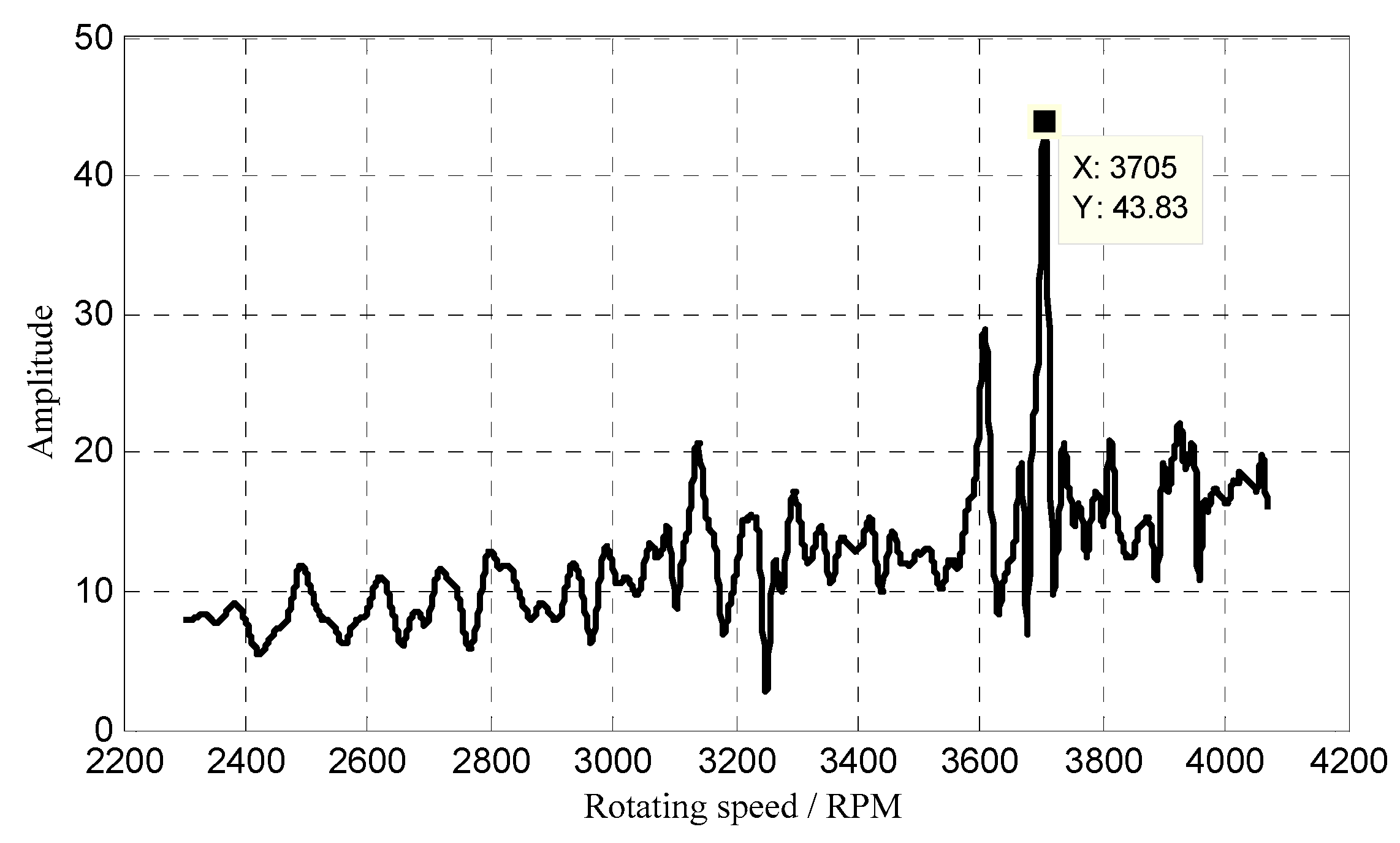
5.3. Experimental Results under Non-Uniform Sensor Configuration
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Song, Z.H. Analysis of Typical Malfunction of Aero Engine; Beijing University of Aeronautics and Astronautics Press: Beijing, China, 1993. [Google Scholar]
- Li, H.K.; He, C.B.; Malekian, R.; Li, Z.X. Weak defect identification for centrifugal compressor blade crack based on pressure sensors and genetic algorithm. Sensors 2018, 18, 1264. [Google Scholar] [CrossRef] [PubMed]
- Ghoshal, A.; Sundaresan, M.; Schulz, M.; Pai, P. Structural health monitoring techniques for wind turbine blades. J. Wind Eng. Ind. Aerodyn. 2000, 85, 309–324. [Google Scholar] [CrossRef]
- Oberholster, A.; Heyns, P. Eulerian laser doppler vibrometry online blade damage identification on a multi-blade test rotor. Mech. Syst. Signal Process. 2011, 25, 344–359. [Google Scholar] [CrossRef]
- Neri, P. Bladed wheels damage detection through non-harmonic Fourier analysis improved algorithm. Mech. Syst. Signal Pocess. 2017, 88, 1–8. [Google Scholar] [CrossRef]
- Neri, P.; Peeters, B. Non-harmonic Fourier analysis for bladed wheels damage detection. J. Sound Vib. 2015, 356, 181–194. [Google Scholar] [CrossRef]
- Oberholster, A.; Heyns, P. A study of the non-harmonic Fourier analysis technique. In Proceedings of the 21st International Congress on Condition Monitoring and Diagnostic Engineering Management, Prague, Czech Republic, 10–13 June 2008; pp. 361–370. [Google Scholar]
- Zhang, J.L.; Duan, F.J.; Niu, G.Y.; Jiang, J.J.; Li, J. A blade tip timing method based on a microwave sensor. Sensors 2017, 17, 1097. [Google Scholar] [CrossRef] [PubMed]
- Gil-Garcia, J.M.; Solis, A.; Aranguren, G.; Zubia, J. An architecture for on-Line measurement of the tip clearance and time of arrival of a bladed disk of an aircraft engine. Sensors 2017, 17, 2162. [Google Scholar] [CrossRef] [PubMed]
- Carrington, I.B.; Wright, J.R.; Cooper, J.E.; Dimitriadis, G. A comparison of blade tip timing data analysis methods. Proc. Inst. Mech. Eng. Part G 2001, 215, 301–312. [Google Scholar] [CrossRef] [Green Version]
- Heath, S.; Imregun, M. A survey of blade tip-timing measurement techniques for turbomachinery vibration. ASME J. Eng. Gas Turbines Power 1998, 120, 784–791. [Google Scholar] [CrossRef]
- Bendali, S.; Joseph, L.; Marc, B.; Philippe, V.; Charles, B. Modal parameter identification of mistuned bladed disks using tip timing data. J. Sound Vib. 2008, 314, 885–906. [Google Scholar]
- Tao, O.Y.; Guo, W.L.; Duan, F.J.; Li, M.L. New method for identifying rotating blades synchronous vibration based on tip-timing. J. Vib. Shock 2011, 30, 249–252. [Google Scholar]
- Lawson, C.; Ivey, P. Tubomachinery blade vibration amplitude measurement through tip timing with capacitance tip clearance probes. Sens. Actuators A Phys. 2005, 118, 14–24. [Google Scholar] [CrossRef]
- Bastami, A.R.; Safarpour, P.; Mikaeily, A.; Mohammadi, M. Identification of asynchronous blade vibration parameters by linear regression of blade tip timing data. ASME J. Eng. Gas Turbines Power 2018, 140, 072506. [Google Scholar] [CrossRef]
- Dimitriadis, G.; Carrington, I.B.; Wright, J.R.; Cooper, J.E. Blade-tip timing measurement of synchronous vibrations of rotating bladed assemblies. Mech. Syst. Signal Process. 2002, 16, 599–622. [Google Scholar] [CrossRef]
- Battiato, G.; Firrone, C.M.; Berruti, T.M. Forced response of rotating bladed disks: Blade tip-timing measurements. Mech. Syst. Signal Process. 2017, 85, 912–926. [Google Scholar] [CrossRef]
- Diamond, D.H.; Heyns, P.S.; Oberholster, A.J. A comparison between three blade tip timing algorithms for estimating synchronous turbomachine blade vibration. In Proceedings of the World Congress on Engineering Asset Management, Pretoria, South Africa, 28–31 October 2014. [Google Scholar]
- Chen, Z.S.; Yang, Y.M.; Guo, B.; Hu, Z. Blade damage prognosis based on kernel principal component analysis and grey model using subsampled tip-timing signals. Proc. Inst. Mech. Eng. Part C J. Mech. 2014, 228, 3178–3185. [Google Scholar]
- Chen, Z.S.; Yang, Y.M.; Xie, Y.; Guo, B.; Hu, Z. Non-contact crack detection of high-speed blades based on principal component analysis and Euclidian angles using optical-fiber sensors. Sens. Actuators A Phys. 2013, 201, 66–72. [Google Scholar] [CrossRef]
- Hu, Z.; Lin, J.; Chen, Z.S.; Yang, Y.M.; Li, X.J. A non-uniformly under-sampled blade tip-timing signal reconstruction method for blade vibration monitoring. Sensors 2015, 15, 2419–2437. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Hu, Z.; Chen, Z.S.; Yang, Y.M.; Xu, H.L. Sparse reconstruction of blade tip-timing signals for multi-mode blade vibration monitoring. Mech. Syst. Signal Process. 2016, 85, 250–258. [Google Scholar] [CrossRef]
- Xu, H.L.; Chen, Z.S.; Xiong, Y.P.; Yang, Y.M.; Tao, L.M. Nonlinear dynamic behaviors of rotated blades with small breathing cracks based on vibration power flow analysis. Shock Vib. 2016, 2016, 4197203. [Google Scholar] [CrossRef]
- Hu, Y.; Tu, X.T.; Li, F.C.; Li, H.G.; Meng, G. An adaptive and tacholess order analysis method based on enhanced empirical wavelet transform for fault detection of bearings with varying speeds. J. Sound Vib. 2017, 409, 241–255. [Google Scholar] [CrossRef]
- Feng, Z.P.; Chen, X.W.; Liang, M. Joint envelope and frequency order spectrum analysis based on iterative generalized demodulation for planetary gearbox fault diagnosis under nonstationary conditions. Mech. Syst. Signal Process. 2016, 16, 242–264. [Google Scholar] [CrossRef]
- Wang, J.; Peng, Y.Y.; Qiao, W. Current-aided order tracking of vibration signals for bearing fault diagnosis of direct-drive wind turbines. IEEE Trans. Ind. Electron. 2016, 63, 6336–6346. [Google Scholar] [CrossRef]
- Wang, J.; Cheng, F.Z.; Qiao, W.; Qu, L.Y. Multiscale filtering reconstruction for wind turbine gearbox fault diagnosis under varying-speed and noisy conditions. IEEE Trans. Ind. Electron. 2018, 65, 4268–4278. [Google Scholar] [CrossRef]
- Sapena-Bano, A.; Burriel-Valencia, J.; Pineda-Sanchez, M.; Puche-Panadero, R.; Riera-Guasp, M. The harmonic order tracking analysis method for the fault diagnosis in induction motors under time-varying conditions. IEEE Trans. Energy Convers. 2017, 32, 244–256. [Google Scholar] [CrossRef]
- Fyfe, K.R.; Munck, E.D.S. Analysis of computed order tracking. Mech. Syst. Signal Process. 1997, 11, 187–205. [Google Scholar] [CrossRef]
- Bossley, K.M.; McKendrick, R.J.; Harris, C.J.; Mercer, C. Hybrid computed order tracking. Mech. Syst. Signal Process. 1999, 13, 627–641. [Google Scholar] [CrossRef]
- Caesarendra, W.; Kosasih, B.; Tieu, A.K.; Moodie, C.A.S. Circular domain features based condition monitoring for low speed slewing bearing. Mech. Syst. Signal Process. 2014, 45, 114–138. [Google Scholar] [CrossRef]
- Coulson, A.J. A generalization of nonuniform bandpass sampling. IEEE Trans. Signal Process. 1995, 43, 694–704. [Google Scholar] [CrossRef]
- Vaughan, R.G.; Scott, L.N.; White, D.R. The theory of bandpass sampling. IEEE Trans. Signal Process. 1991, 39, 1973–1984. [Google Scholar] [CrossRef]












| Parameters | Values |
|---|---|
| Blade material | 40 Cr steel |
| Blade length | 34 mm |
| Blade width | 11 mm |
| Blade thickness | 3 mm |
| Blade tip radius | 103 mm |
| Different Methods | Resonant Frequency | Absolute Errors |
|---|---|---|
| Theoretical calculation | 2140.4 Hz | – |
| The GARIV method | 2270 Hz | 6.05% |
| Algorithm in Section 3.1 | 2226 Hz | 4.00% |
| Algorithm in Section 3.2 | 2223 Hz | 3.86% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Liu, J.; Zhan, C.; He, J.; Wang, W. Reconstructed Order Analysis-Based Vibration Monitoring under Variable Rotation Speed by Using Multiple Blade Tip-Timing Sensors. Sensors 2018, 18, 3235. https://doi.org/10.3390/s18103235
Chen Z, Liu J, Zhan C, He J, Wang W. Reconstructed Order Analysis-Based Vibration Monitoring under Variable Rotation Speed by Using Multiple Blade Tip-Timing Sensors. Sensors. 2018; 18(10):3235. https://doi.org/10.3390/s18103235
Chicago/Turabian StyleChen, Zhongsheng, Jianhua Liu, Chi Zhan, Jing He, and Weimin Wang. 2018. "Reconstructed Order Analysis-Based Vibration Monitoring under Variable Rotation Speed by Using Multiple Blade Tip-Timing Sensors" Sensors 18, no. 10: 3235. https://doi.org/10.3390/s18103235
APA StyleChen, Z., Liu, J., Zhan, C., He, J., & Wang, W. (2018). Reconstructed Order Analysis-Based Vibration Monitoring under Variable Rotation Speed by Using Multiple Blade Tip-Timing Sensors. Sensors, 18(10), 3235. https://doi.org/10.3390/s18103235





