Weighted Measurement Fusion Particle Filter for Nonlinear Systems with Correlated Noises
Abstract
:1. Introduction
2. Problem Formulation
3. Weighted Measurement Fusion Particle Filter (WMF-PF) Algorithm
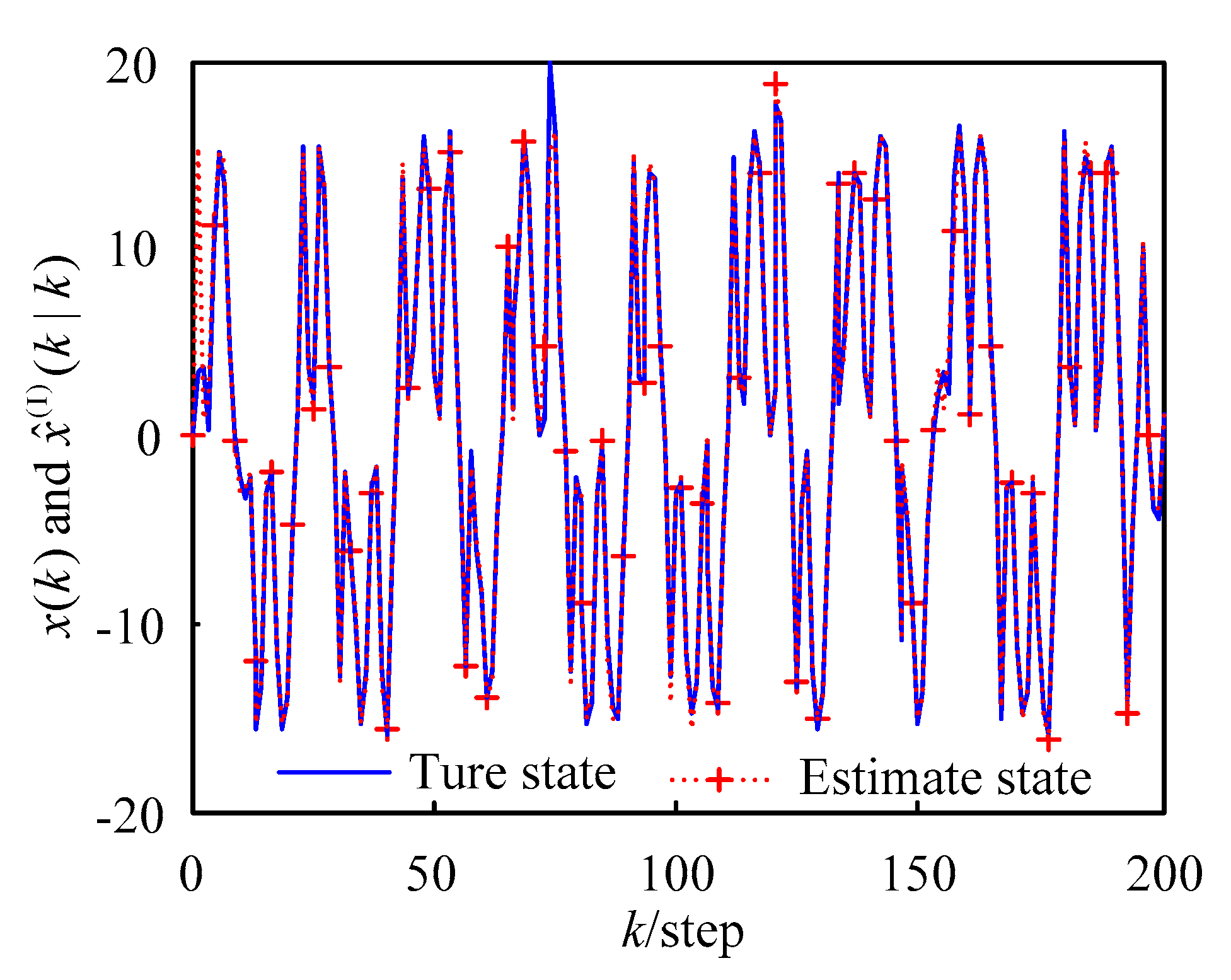
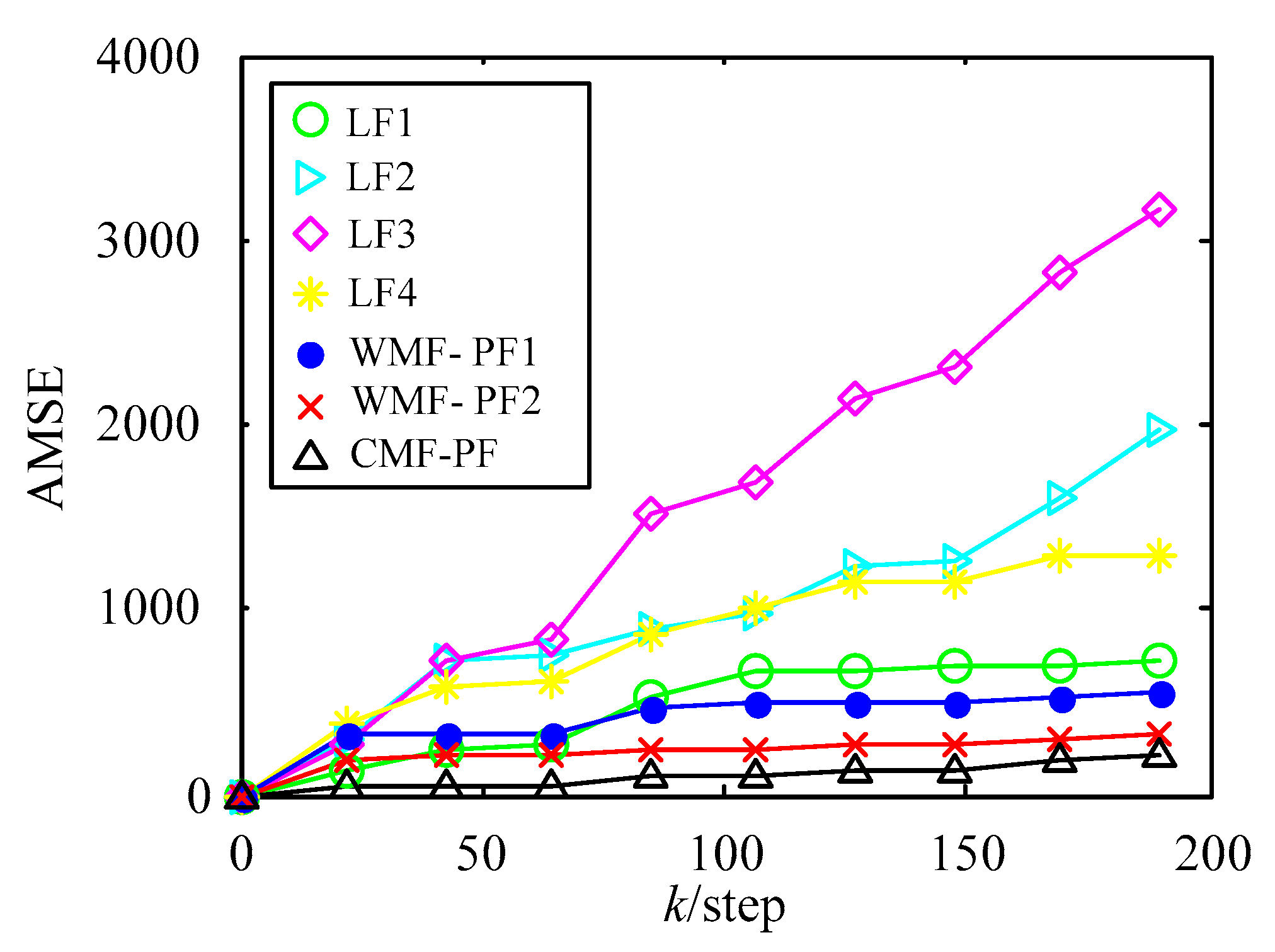
4. Simulation Example
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bar-Shalom, Y.; Li, X.R. Multitarget-Multisensor Tracking: Principles and Techniques; YBS Publishing: Storrs, CT, USA, 1995. [Google Scholar]
- Arasaratnam, I.; Haykin, S.; Thomas, R.H. Cubature Kalman filtering for continuous-discrete systems: Theory and simulations. IEEE Trans. Signal Process. 2010, 58, 4977–4993. [Google Scholar] [CrossRef]
- Strano, S.; Terzo, M. Accurate state estimation for a hydraulic actuator via a SDRE nonlinear filter. Mech. Syst. Signal Process. 2016, 75, 576–588. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Guida, D. A time-domain system identification numerical procedure for obtaining linear dynamical models of multibody mechanical systems. Arch. Appl. Mech. 2018, 88, 1325–1347. [Google Scholar] [CrossRef]
- Caracciolo, R.; Richiedei, D.; Trevisani, A. Robust piecewise-linear state observers for flexible link mechanisms. J. Dyn. Syst. Meas. Control 2008, 130, 928–950. [Google Scholar] [CrossRef]
- Pappalard, C.M.; Guida, D. System identification algorithm for computing the modal parameters of linear. Machines 2018, 6, 12. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Guida, D. System identification and experimental modal analysis of a frame structure. Eng. Lett. 2018, 26, 56–68. [Google Scholar]
- Wang, S.Y.; Feng, J.C.; Tse, C.K. Novel cubature Kalman filtering for systems involving nonlinear states and linear measurements. Int. J. Electron. Commun. 2015, 69, 314–320. [Google Scholar] [CrossRef]
- Calabrese, A.; Strano, S.; Serino, G.; Terzo, M. An extended Kalman Filter procedure for damage detection of base-isolated structures. In Proceedings of the 2014 IEEE Workshop on Environmental, Energy, and Structural Monitoring Systems, Naples, Italy, 17–18 September 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Gobbo, D.D.; Napolitano, M.; Famouri, P.; Innocenti, M. Experimental application of extended Kalman filtering for sensor validation. IEEE Trans. Control Syst. Technol. 2001, 9, 376–380. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. A new extension of the Kalman filter to nonlinear systems. In Proceedings of the International Symposium on Aerospace/Defense Sensing, Simulation and Controls, Orlando, FL, USA, 28 July 1997; pp. 182–193. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Hammersley, J.M.; Morton, K.W. Poor man’s Monte Carlo. J. R. Stat. Soc. B 1954, 16, 786–802. [Google Scholar]
- Doucet, A.; Freitas, N.D.; Gordon, N. Sequential Monte Carlo Methods in Practice, Statistics for Engineering and Information Science; Springer: New York, NY, USA, 2001. [Google Scholar]
- Berg, B.A. Markov Chain Monte Carlo Simulations and Their Statistical Analysis; World Scientific: Singapore, 2004. [Google Scholar]
- Ge, Q.B.; Shao, T.; Yang, Q.; Shen, X.; Wen, C.L. Multisensor nonlinear fusion methods based on adaptive ensemble fifth-degree iterated Cubature information filter for biomechatronics. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 912–925. [Google Scholar] [CrossRef]
- Crisan, D.; Doucet, A. A survey of convergence results on Particle filtering methods for practitioners. IEEE Trans. Signal Process. 2002, 50, 736–746. [Google Scholar] [CrossRef]
- Bruno, M.G.S.; Pavlov, A. Improved particle filters for ballistic target tracking. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Montreal, QC, Canada, 17–21 May 2004; pp. 17–21. [Google Scholar]
- Gordon, N.; Salmond, D.J.; Smith, A.F.M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation. IEEE Proc. Radar Signal Process. 2002, 140, 107–113. [Google Scholar] [CrossRef]
- Ge, Q.B.; Shao, T.; Chen, S.D.; Wen, C.L. Carrier Tracking Estimation Analysis by Using the Extended Strong Tracking Filtering. IEEE Trans. Ind. Electron. 2017, 64, 1415–1424. [Google Scholar] [CrossRef]
- Sun, S.L.; Lin, H.L.; Ma, J.; Li, X.Y. Multi-sensor distributed fusion estimation with applications in networked systems: A review paper. Inf. Fusion 2017, 38, 122–134. [Google Scholar] [CrossRef]
- Gispan, L.; Leshem, A.; Be’ery, Y. Decentralized estimation of regression coefficients in sensor networks. Digit. Signal Process. 2017, 68, 16–23. [Google Scholar] [CrossRef]
- Sun, S.L.; Deng, Z.L. Multi-sensor optimal information fusion Kalman filter. Automatica 2004, 40, 1017–1023. [Google Scholar] [CrossRef]
- Pastorino, R.; Richiedei, D.; Cuadrado, J.; Trevisani, A. State estimation using multibody models and non-linear Kalman filters. Int. J. Non-Linear Mech. 2013, 53, 83–90. [Google Scholar] [CrossRef]
- Ma, J.; Sun, S.L. Information fusion estimators for systems with multiple sensors of different packet dropout rates. Inf. Fusion 2011, 12, 213–222. [Google Scholar] [CrossRef]
- Tian, T.; Sun, S.L.; Li, N. Multi-sensor information fusion estimators for stochastic uncertain systems with correlated noises. Inf. Fusion 2016, 27, 126–137. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, Q.D.; Sun, S.L. Weighted measurement fusion estimation algorithm with correlated noises and its global optimality. Syst. Eng. Electron. 2010, 32, 2057–2061. [Google Scholar] [CrossRef]
- Wang, X.; Sun, S.L.; Ding, K.H.; Xue, J.Y. Weighted measurement fusion white noise deconvolution Filter with correlated noise for multisensor stochastic systems. Math. Probl. Eng. 2012, 21, 857–868. [Google Scholar] [CrossRef]
- Wang, X.X.; Zhao, L.; Xia, Q.X.; Cao, W.; Li, L. Design of unscented Kalman filter with correlative noises. Control Theory Appl. 2010, 27, 1362–1368. [Google Scholar]
- Wang, X.X.; Zhao, L.; Pan, Q.; Xia, Q.X.; Hong, W. Design of UKF with correlative noises based on minimum mean square error estimation. Control Decis. 2010, 25, 1393–1398. [Google Scholar] [CrossRef]
- Qian, H.M.; Ge, L.; Huang, W.; Liu, X. Design of CKF with correlative noises based on Bayesian estimation, systems engineering and electronics. Syst. Eng. Electron. 2012, 34, 2214–2218. [Google Scholar] [CrossRef]
- Wang, X.X.; Liang, Y.; Pan, Q.; Zhao, C.H.; Yang, F. Design and implementation of Gaussian filter for nonlinear system with randomly delayed measurements and correlated noises. Appl. Math. Comput. 2014, 232, 1011–1024. [Google Scholar] [CrossRef]
- Wang, X.X.; Liang, Y.; Pan, Q.; Yang, F. A Gaussian approximation recursive filter for nonlinear systems with correlated noises. Automatica 2012, 48, 2290–2297. [Google Scholar] [CrossRef]
- Xu, J.H.; Dimirovski, G.M.; Jing, Y.W.; Shen, C. UKF design and stability for nonlinear stochastic systems with correlated noises. In Proceedings of the 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 2–14 December 2007; pp. 6226–6231. [Google Scholar] [CrossRef]
- Fu, A.; Zhu, Y.M.; Song, E. The optimal Kalman type state estimator with multi-step correlated process and measurement noises. In Proceedings of the 2008 International Conference on Embedded Software and Systems, Chengdu, China, 22–26 September 2008; pp. 215–220. [Google Scholar] [CrossRef]
- Huang, Y.L.; Zhang, Y.G.; Wang, X.X.; Zhao, L. Gaussian filter for nonlinear systems with correlated noises at the same epoch. Automatica 2015, 60, 122–126. [Google Scholar] [CrossRef]
- Song, E.B.; Zhu, Y.M.; Zhou, J. Sensors’ optimal dimensionality compression matrix in estimation fusion. Automatica 2005, 41, 2131–2139. [Google Scholar] [CrossRef]
- Ran, C.J.; Hui, Y.S.; Gu, L.; Deng, Z.L. Correlated measurement fusion steady-state Kalman filtering algorithms and their optimality. Acta Autom. Sin. 2008, 34, 233–239. [Google Scholar] [CrossRef]
- Duan, Z.S.; Han, C.Z. Multisensor centralized fusion tracking with correlated measurement noises. Syst. Eng. Electron. 2005, 27, 1160–1163. [Google Scholar]
- Ou, L.J.; Qiu, H.Z.; Zhang, H.Y. Multiple correlated measurements fusion algorithm and its optimality. Inf. Control 2005, 34, 690–695. [Google Scholar] [CrossRef]
- Gan, Q.; Harris, C.J. Comparison of two measurement fusion methods for Kalman filter based multisensor data fusion. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 273–279. [Google Scholar] [CrossRef]
- Kitagawa, G. Non-Gaussian state space modeling of time series. In Proceedings of the 26th Conference on decision and Control, Los Angeles, CA, USA, 9–11 December 1987; pp. 1700–1705. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.W.; Hao, G.; Sun, S.L. Weighted Measurement Fusion Particle Filter for Nonlinear Systems with Correlated Noises. Sensors 2018, 18, 3242. https://doi.org/10.3390/s18103242
Zhang KW, Hao G, Sun SL. Weighted Measurement Fusion Particle Filter for Nonlinear Systems with Correlated Noises. Sensors. 2018; 18(10):3242. https://doi.org/10.3390/s18103242
Chicago/Turabian StyleZhang, Ke Wei, Gang Hao, and Shu Li Sun. 2018. "Weighted Measurement Fusion Particle Filter for Nonlinear Systems with Correlated Noises" Sensors 18, no. 10: 3242. https://doi.org/10.3390/s18103242
APA StyleZhang, K. W., Hao, G., & Sun, S. L. (2018). Weighted Measurement Fusion Particle Filter for Nonlinear Systems with Correlated Noises. Sensors, 18(10), 3242. https://doi.org/10.3390/s18103242




