An Improved Strapdown Inertial Navigation System Initial Alignment Algorithm for Unmanned Vehicles
Abstract
:1. Introduction
2. Background Knowledge
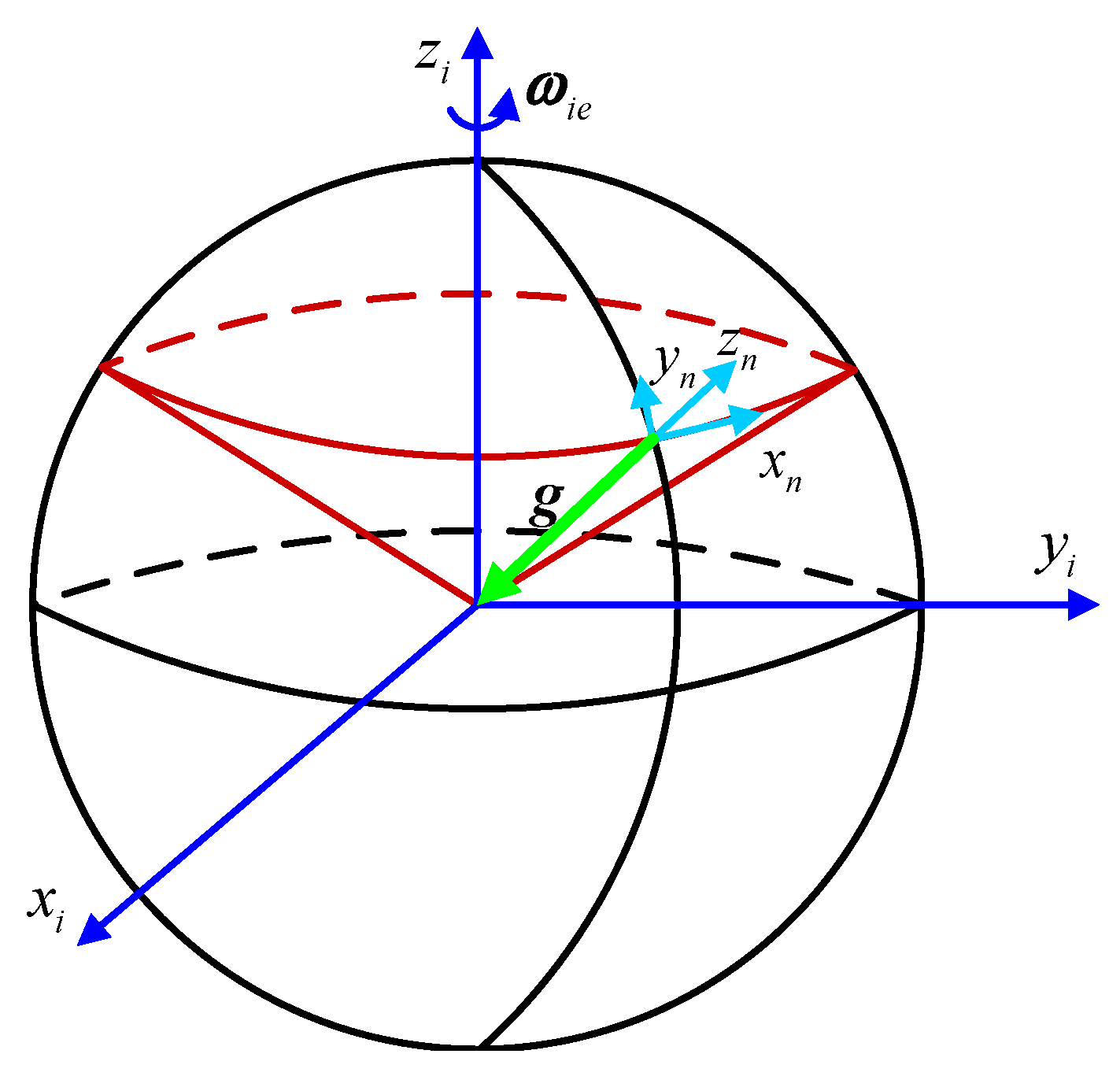
2.1. Analytical Coarse Alignment Algorithm Based on the Solidification Coordinate Frame
2.2. Integrated Fine Alignment Algorithm Based on the CKF Method
2.2.1. Nonlinear Model for Integrated Fine Alignment of SINS/ GNSS Integrated Navigation Systems
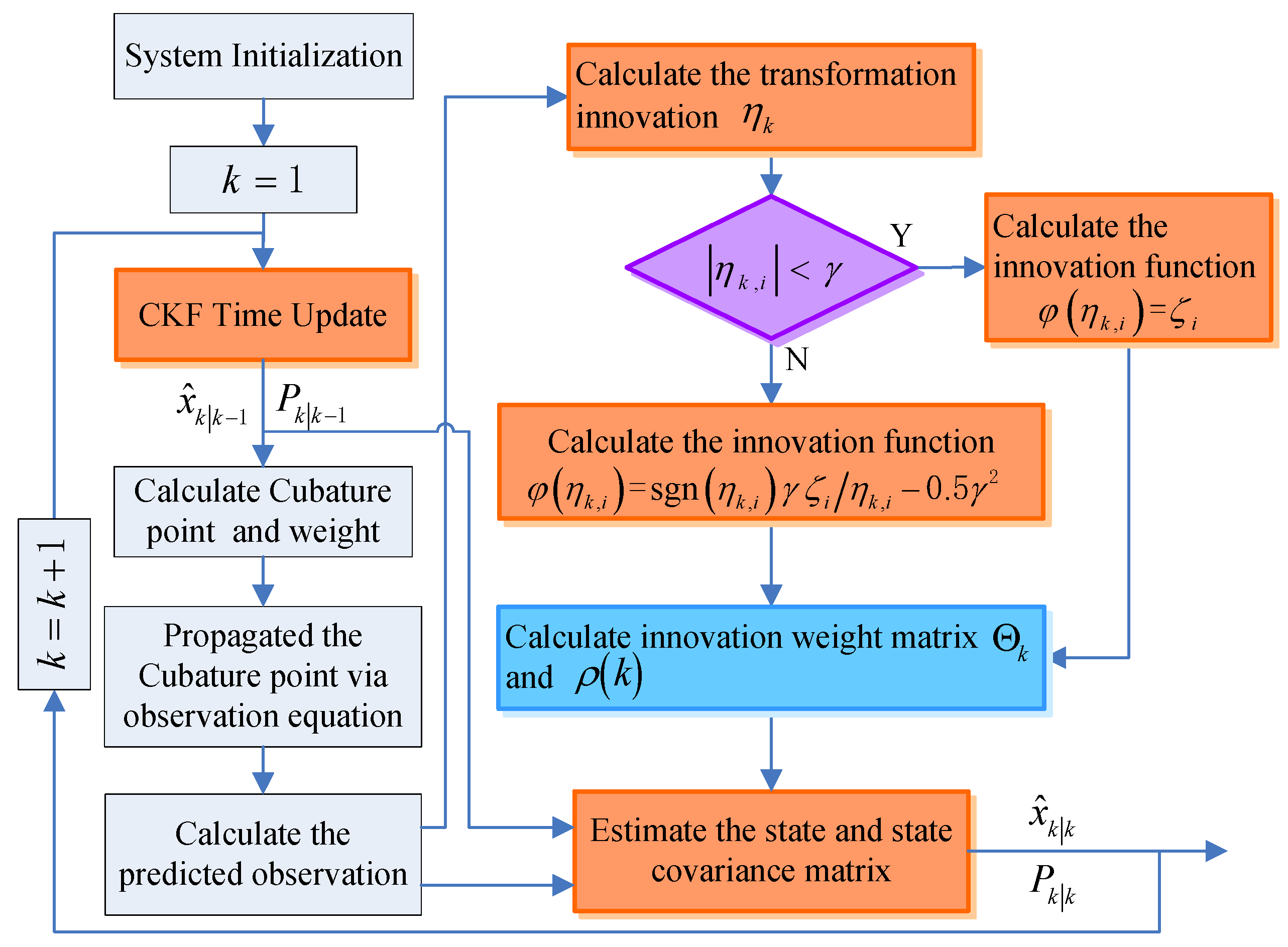
2.2.2. Nonlinear Filter Algorithm Based on CKF
| Algorithm 1 CKF algorithm |
|
3. Initial Alignment Algorithm for the Unmanned Vehicle
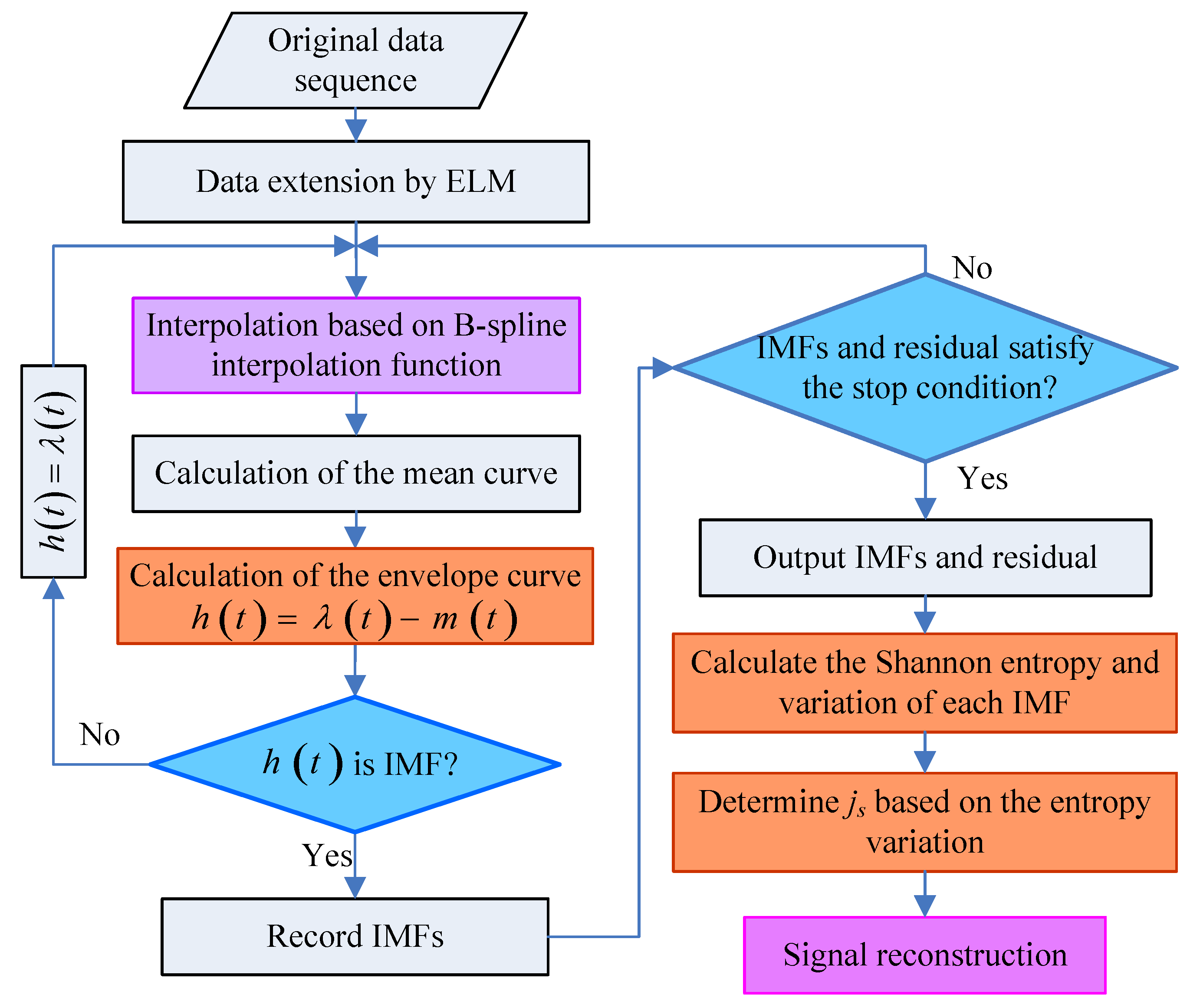
3.1. Improved Denoising Method Based on the ELM and EMD–Shannon Method
3.1.1. A Brief Review of the EMD Method
- In the entire data set, the difference between the number of extreme values and the number of zero crossings must not be greater than one;
- At any point of the data set, the mean value of the envelope defined by the local extrema is all zero.
- First of all, all local extreme values of the signal should be found out and identified. The cubic spline line is used to connect all the local maxima and all the local minima, producing the upper envelope and the lower envelope, respectively. Thus, all of the signal data should be covered by the upper and lower envelopes. We suppose that is the mean of the covered data by the envelopes, so the difference between the signal and the mean can be taken as a new signal, indicated as , named the first component:
- In general, we can not guarantee that is a stationary data sequence, so we should repeat the above operation. Now, is taken as a new signal and its envelope mean is . Thus, the data sequence after removing the low-frequency components represented by is :Repeating the above operation up to k times, we can obtain the signal and the first IMF as follows:
- Finally, the residual is a new signal that removed the high frequency component from the original signal:
- Then, we can deal with the residual iteratively to get the other IMFs. The stop iterating condition is that when the residue becomes a monotonic function or a function with only one extremum. It means that no more IMF can be extracted from the residual signal . Thus, after the decomposition, is decomposed into several IMFs and a residual:
3.1.2. Improved EMD Denoising Method Based on ELM and Shannon Entropy
- Step 1:
- Extend the time series to the right and seven adjacent samples are used as the input of the ELM method. Use the adjacent right (or left) samples as a training sample.
- Step 2:
- Add the previous prediction value into each new learning before each step of learning. Repeatedly training and learning, obtain all the required extension sequence according to the required extension of the extreme points.
- Step 3:
- Decompose the inertial sensor signal into several IMFs and residuals by using the EMD method.
- Step 4:
- Calculate the Shannon entropy of each IMF .
- Step 5:
- Calculate the adjacent Shannon entropy variation .
- Step 6:
- Determine the value of based on Step 5.
- Step 7:
- Reconstruct the signal based on the value of .
3.2. Improved Robust Filter based on the RHCKF Method for Fine Alignment
3.3. Improved Initial Alignment Algorithm Based on ELMEMD-Shannon and RHCKF Methods
| Algorithm 2 Improved Initial Alignment Algorithm |
|
4. Test Result and Analysis
4.1. Static Test in the Laboratory
4.1.1. Test Environment Establishment
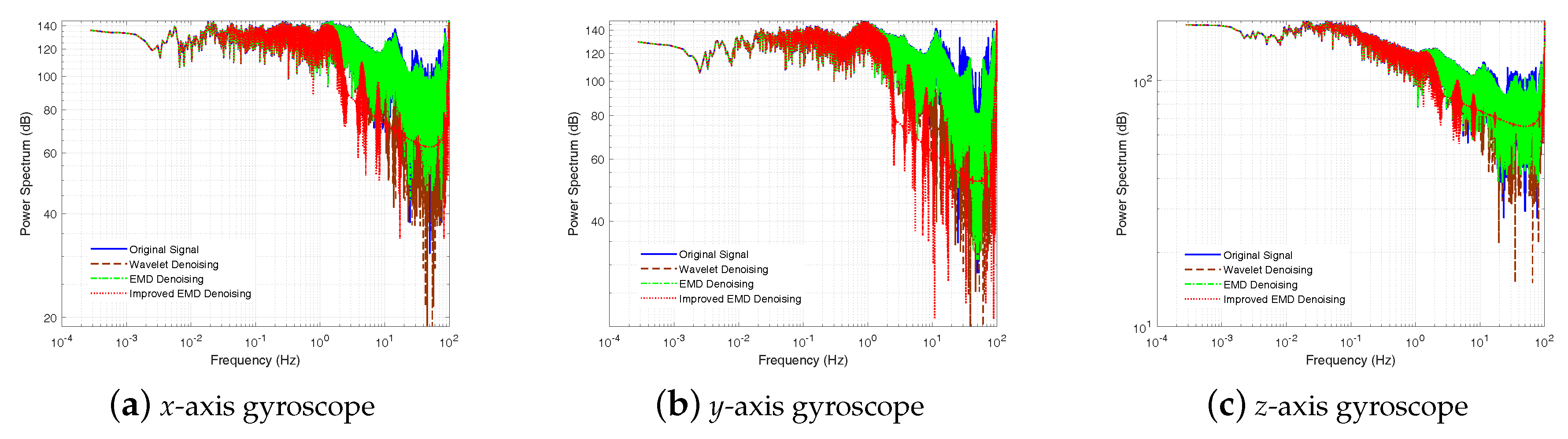
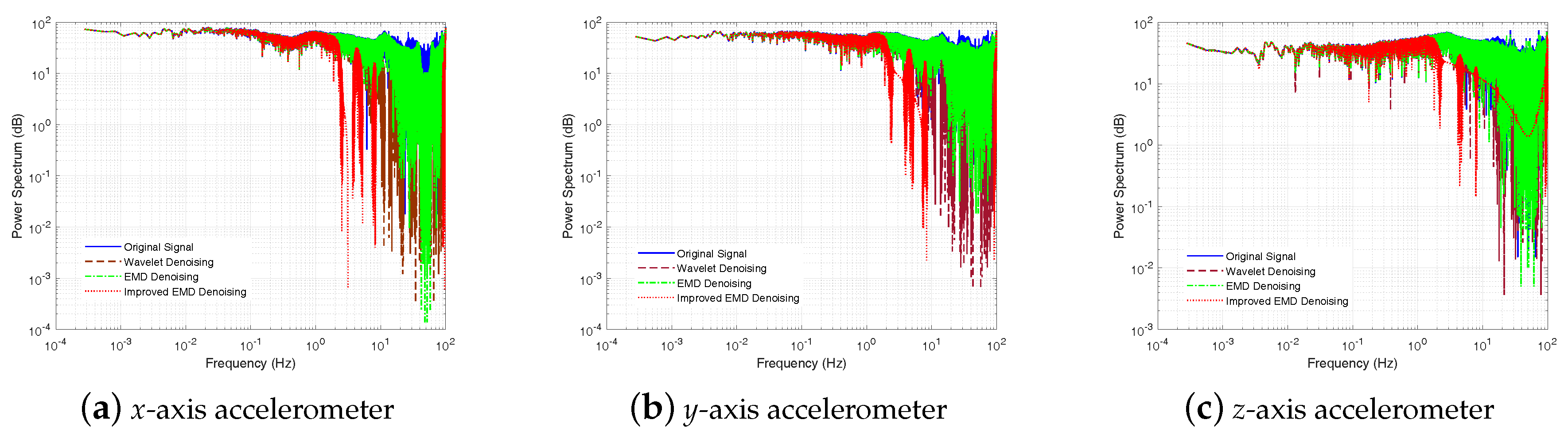
4.1.2. Static Test Results and Analysis
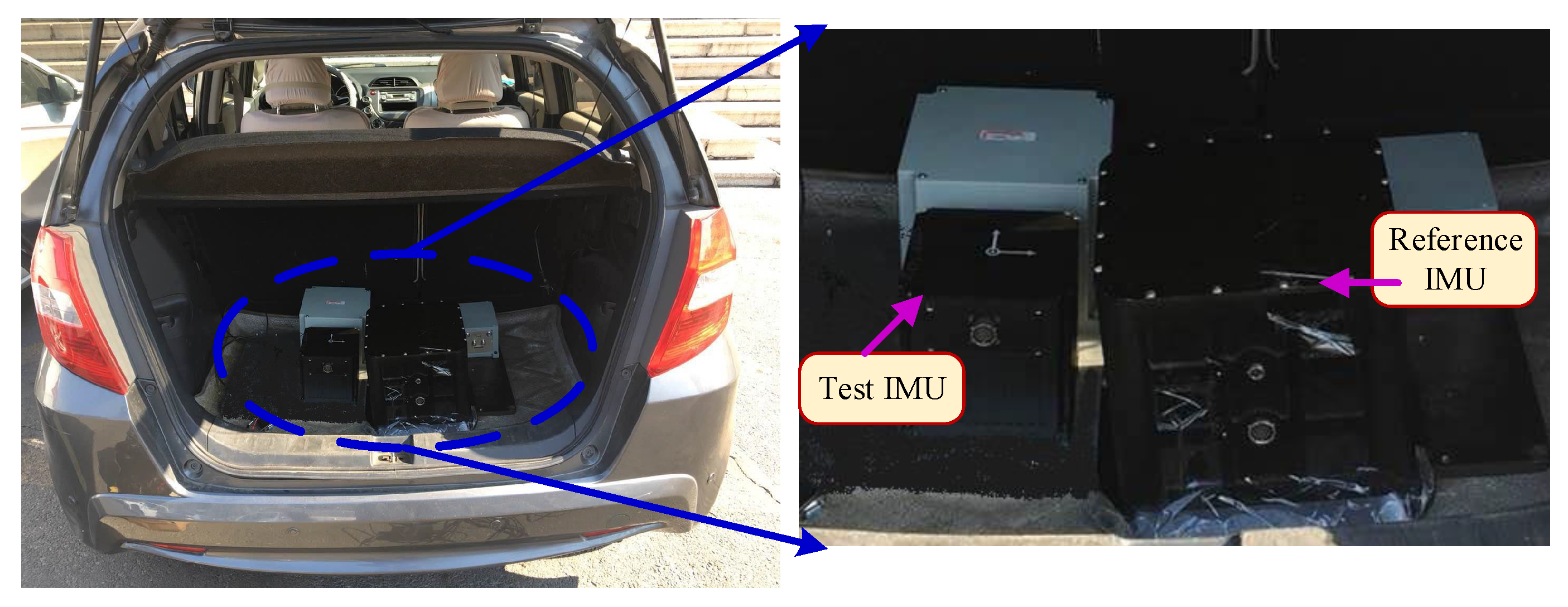
4.2. Dynamic Test in Vehicle
4.2.1. Test Environment Establishment
4.2.2. Result and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sun, Q.; Zhang, Y.; Wang, J.; Gao, W. An Improved FAST Feature Extraction based on RANSAC Method of Vision/SINS Integrated Navigation System in GNSS-Denied Environments. Adv. Space Res. 2017, 60, 2660–2671. [Google Scholar] [CrossRef]
- Sun, Q.; Diao, M.; Zhang, Y.; Li, Y. Cooperative Localization Algorithm for Multiple Mobile Robot System in Indoor Environment Based on Variance Component Estimation. Symmetry 2017, 9, 94. [Google Scholar] [CrossRef]
- Yu, F.; Sun, Q.; Lv, C.; Ben, Y.; Fu, Y. A SLAM Algorithm Based on Adaptive Cubature Kalman Filter. Math. Probl. Eng. 2014, 2014, 1–11. [Google Scholar] [CrossRef]
- Petritoli, E.; Giagnacovo, T.; Leccese, F. Lightweight GNSS/IRS integrated navigation system for UAV vehicles. In Proceedings of the 2014 IEEE Metrology for Aerospace (MetroAeroSpace), Benevento, Italy, 29–30 May 2014; pp. 56–61. [Google Scholar]
- Hinüber, E.L.; Reimer, C.; Schneider, T.; Stock, M. INS/GNSS Integration for Aerobatic Flight Applications and Aircraft Motion Surveying. Sensors 2017, 17, 941. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Tian, Y.; Diao, M. Cooperative Localization Algorithm based on Hybrid Topology Architecture for Multiple Mobile Robot System. IEEE Int. Things J. 2018. [Google Scholar] [CrossRef]
- Wu, M.; Wu, Y.; Hu, X.; Hu, D. Optimization-based alignment for inertial navigation systems: Theory and algorithm. Aerosp. Sci. Technol. 2011, 15, 1–17. [Google Scholar] [CrossRef]
- Chang, L.; Li, J.; Chen, S. Initial Alignment by Attitude Estimation for Strapdown Inertial Navigation Systems. IEEE Trans. Instrum. Meas. 2015, 64, 784–794. [Google Scholar] [CrossRef]
- Silson, P.M.G. Coarse Alignment of a Ship’s Strapdown Inertial Attitude Reference System Using Velocity Loci. IEEE Trans. Instrum. Meas. 2011, 60, 1930–1941. [Google Scholar] [CrossRef]
- Wu, Y.; Pan, X. Velocity/Position Integration Formula Part I: Application to In-Flight Coarse Alignment. IEEE Trans. Aerosp. Electron. Syst. 2012, 49, 1006–1023. [Google Scholar] [CrossRef]
- Fang, J.; Yang, S. Study on Innovation Adaptive EKF for In-Flight Alignment of Airborne POS. IEEE Trans. Instrum. Meas. 2011, 60, 1378–1388. [Google Scholar]
- Dong, Q.; Li, Y.; Sun, Q.; Zhang, Y. An Adaptive Initial Alignment Algorithm Based on Variance Component Estimation for a Strapdown Inertial Navigation System for AUV. Symmetry 2017, 9, 129. [Google Scholar] [CrossRef]
- Niu, C.; Li, Y.; Hu, R.Q.; Ye, F. Fast and Efficient Radio Resource Allocation in Dynamic Ultra-Dense Heterogeneous Networks. IEEE Access 2017, 5, 1911–1924. [Google Scholar] [CrossRef]
- El-Sheimy, N.; Nassar, S.; Noureldin, A. Wavelet de-noising for IMU alignment. IEEE Aerosp. Electron. Syst. Mag. 2004, 19, 32–39. [Google Scholar] [CrossRef]
- Cui, B.; Chen, X. Improved hybrid filter for fiber optic gyroscope signal denoising based on EMD and forward linear prediction. Sens. Actuators A Phys. 2015, 230, 150–155. [Google Scholar] [CrossRef]
- Gan, Y.; Sui, L.; Wu, J.; Wang, B.; Zhang, Q.; Xiao, G. An EMD threshold de-noising method for inertial sensors. Measurement 2014, 49, 34–41. [Google Scholar] [CrossRef]
- Ayachi, F.; Nguyen, H.; Goubault, E.; Boissy, P.; Duval, C. The Use of Empirical Mode Decomposition-Based Algorithm and Inertial Measurement Units to Auto-Detect Daily Living Activities of Healthy Adults. IEEE Trans. Neural Syst. Rehabil. Eng. A Publ. IEEE Eng. Med. Biol. Soc. 2016, 24, 1060–1070. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.J.; Agrawal, V.; Gaunaurd, I.; Gailey, R.; Bennett, C. Missing Sample Recovery for Wireless Inertial Sensor-Based Human Movement Acquisition. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 1191. [Google Scholar] [CrossRef] [PubMed]
- Vincent, B.; Sofiane, R.; Christine, A.C.; Philippe, F.; Claudia, M.; Aurelio, C. Integration of Human Walking Gyroscopic Data Using Empirical Mode Decomposition. Sensors 2013, 14, 370–381. [Google Scholar] [Green Version]
- Wang, L.; Li, S. Enhanced multi-sensor data fusion methodology based on multiple model estimation for integrated navigation system. Int. J. Control Autom. Syst. 2018, 16, 295–305. [Google Scholar] [CrossRef]
- Gong, X.; Zhang, J.; Fang, J. A Modified Nonlinear Two-Filter Smoothing for High-Precision Airborne Integrated GPS and Inertial Navigation. IEEE Trans. Instrum. Meas. 2015, 64, 3315–3322. [Google Scholar] [CrossRef]
- Xu, X.; Xu, X.; Zhang, T.; Li, Y.; Tong, J. A Kalman Filter for SINS Self-Alignment Based on Vector Observation. Sensors 2017, 17, 264. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Jia, Y. A nonlinear quaternion-based fault-tolerant SINS/GNSS integrated navigation method for autonomous UAVs. Aerosp. Sci. Technol. 2015, 40, 191–199. [Google Scholar] [CrossRef]
- Ali, J.; Mirza, M.R.U.B. Performance comparison among some nonlinear filters for a low cost SINS/GPS integrated solution. Nonlinear Dyn. 2010, 61, 491–502. [Google Scholar] [CrossRef]
- Chang, L.; Li, J.; Li, K. Optimization-based Alignment for Strapdown Inertial Navigation System: Comparison and Extension. IEEE Trans. Aerosp. Electron. Syst. 2014, 52, 1697–1713. [Google Scholar] [CrossRef]
- Zhang, M.; Wen, Y.; Chen, J.; Yang, X.; Gao, R.; Zhao, H. Pedestrian Dead-Reckoning Indoor Localization Based on OS-ELM. IEEE Access 2018, 6, 6116–6129. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, Y.; Wang, J. Research on Initial Alignment and Self-Calibration of Rotary Strapdown Inertial Navigation Systems. Sensors 2015, 15, 3154–3171. [Google Scholar] [CrossRef] [PubMed]
- Sun, G.; Wang, M.; Huang, L.; Shen, L. Generating Multi-Scroll Chaotic Attractors via Switched Fractional Systems. Circ. Syst. Signal Process. 2011, 30, 1183–1195. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, Y.; Wang, J. A strapdown interial navigation system/Beidou/Doppler velocity log integrated navigation algorithm based on a Cubature Kalman filter. Sensors 2014, 14, 1511–1527. [Google Scholar] [CrossRef] [PubMed]
- Abdolkarimi, E.S.; Abaei, G.; Mosavi, M.R. A wavelet-extreme learning machine for low-cost INS/GPS navigation system in high-speed applications. GPS Solut. 2018, 22, 15. [Google Scholar] [CrossRef]
- Chang, L.; Li, K.; Hu, B. Huber’s M-Estimation-Based Process Uncertainty Robust Filter for Integrated INS/GPS. IEEE Sens. J. 2015, 15, 3367–3374. [Google Scholar] [CrossRef]
- Xu, X.; Xu, X.; Yao, Y.; Wang, Z. In-motion coarse alignment method based on reconstructed observation vectors. Rev. Sci. Instrum. 2017, 88, 035001. [Google Scholar] [CrossRef] [PubMed]

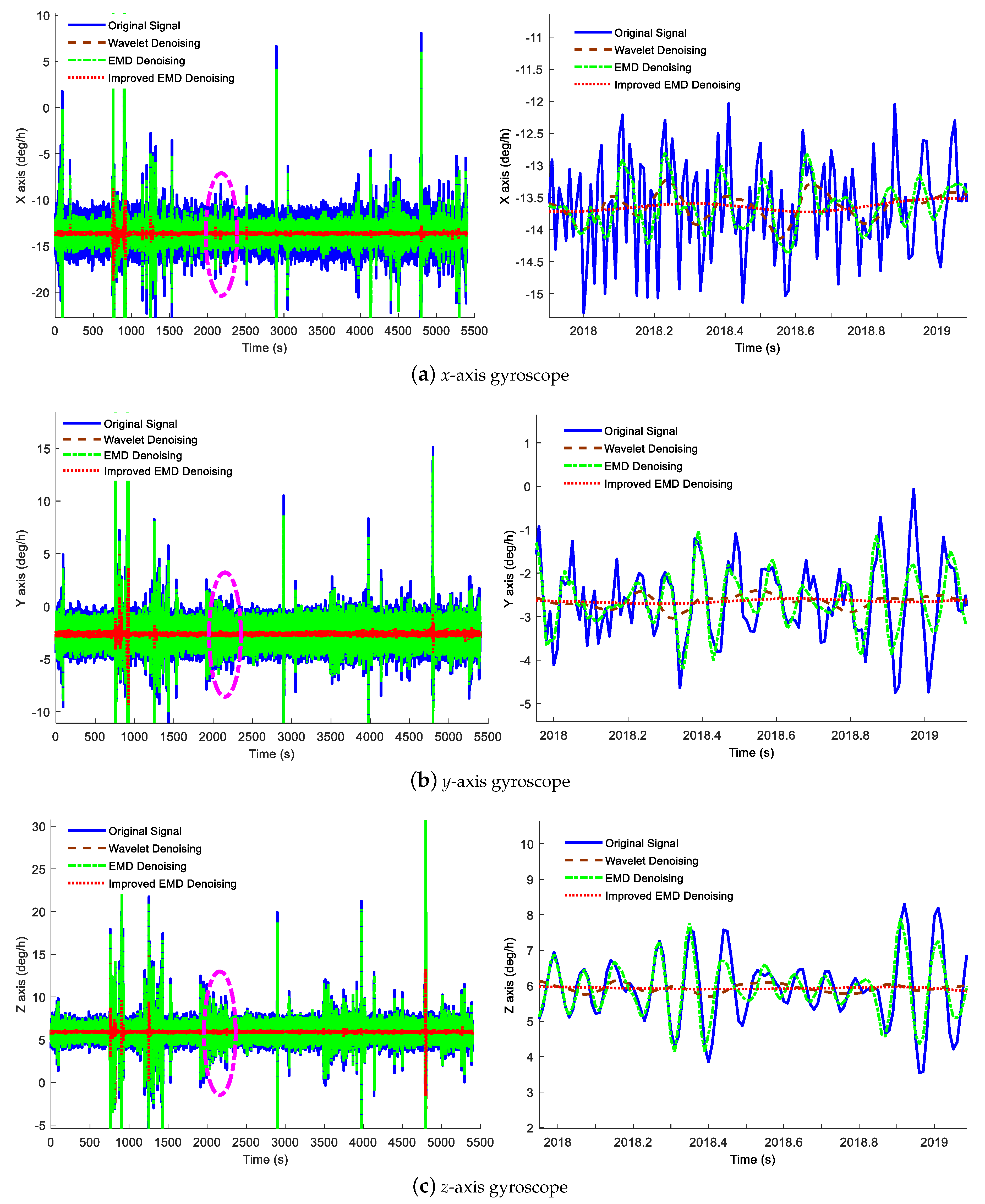



| Orignal | Wavelet | EMD | ELMEMD-Shannon | |
|---|---|---|---|---|
| QN (deg/h) | 0.00827 | 0.00202 | 0.00599 | 0.00012 |
| RAW (deg/) | 0.00277 | 0.00056 | 0.00182 | 0.00010 |
| BI (deg/h) | 0.28702 | 0.13535 | 0.09335 | 0.07795 |
| ARW (deg/h/) | 0.58961 | 1.24727 | 0.40130 | 0.33749 |
| RR (deg/h/h) | 1.53834 | 0.72803 | 0.49311 | 0.41639 |
| Orignal | Wavelet | EMD | ELMEMD-Shannon | |
|---|---|---|---|---|
| QN (deg/h) | 0.00785 | 0.00209 | 0.00663 | 0.00020 |
| RAW (deg/) | 0.00245 | 0.00058 | 0.00198 | 0.00012 |
| BI (deg/h) | 0.20602 | 0.13690 | 0.09408 | 0.09006 |
| ARW (deg/h/) | 0.59640 | 0.89345 | 0.40294 | 0.39058 |
| RR (deg/h/h) | 1.10144 | 0.73614 | 0.49505 | 0.48154 |
| Orignal | Wavelet | EMD | ELMEMD-Shannon | |
|---|---|---|---|---|
| QN (deg/h) | 0.00743 | 0.00170 | 0.00617 | 0.00037 |
| RAW (deg/) | 0.00226 | 0.00046 | 0.00185 | 0.00016 |
| BI (deg/h) | 0.19115 | 0.13484 | 0.09195 | 0.08868 |
| ARW (deg/h/) | 0.58718 | 0.82919 | 0.39492 | 0.42828 |
| RR (deg/h/h) | 1.02223 | 0.72478 | 0.48544 | 0.52824 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Yu, F.; Gao, W.; Wang, Y. An Improved Strapdown Inertial Navigation System Initial Alignment Algorithm for Unmanned Vehicles. Sensors 2018, 18, 3297. https://doi.org/10.3390/s18103297
Zhang Y, Yu F, Gao W, Wang Y. An Improved Strapdown Inertial Navigation System Initial Alignment Algorithm for Unmanned Vehicles. Sensors. 2018; 18(10):3297. https://doi.org/10.3390/s18103297
Chicago/Turabian StyleZhang, Ya, Fei Yu, Wei Gao, and Yanyan Wang. 2018. "An Improved Strapdown Inertial Navigation System Initial Alignment Algorithm for Unmanned Vehicles" Sensors 18, no. 10: 3297. https://doi.org/10.3390/s18103297
APA StyleZhang, Y., Yu, F., Gao, W., & Wang, Y. (2018). An Improved Strapdown Inertial Navigation System Initial Alignment Algorithm for Unmanned Vehicles. Sensors, 18(10), 3297. https://doi.org/10.3390/s18103297





