A Mathematical Model of a Piezo-Resistive Eight-Beam Three-Axis Accelerometer with Simulation and Experimental Validation
Abstract
:1. Introduction
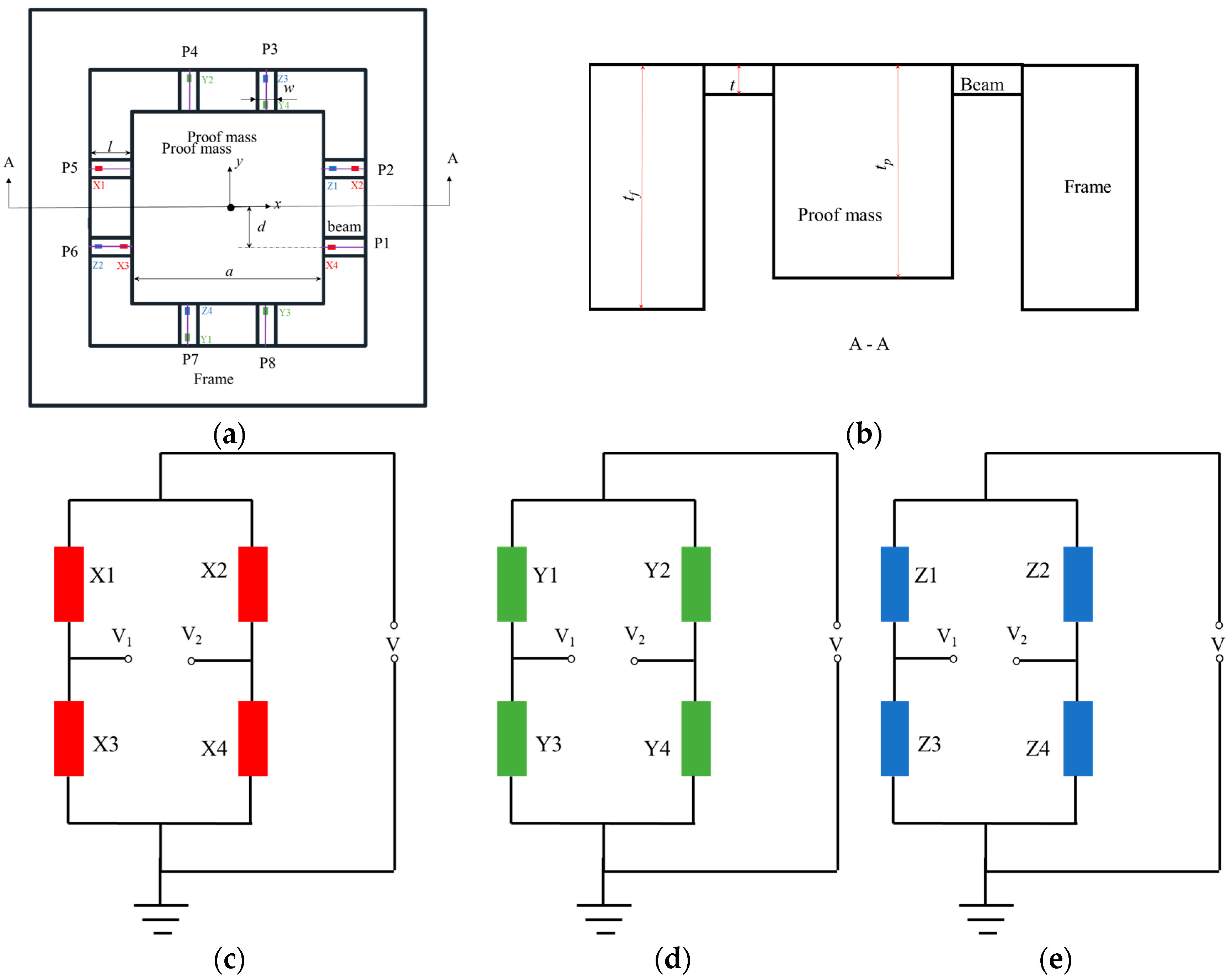
2. Modeling Piezo-Resistive Eight-Beam Three-Axis Accelerometer
2.1. Modeling the Static Behavior
2.1.1. Acceleration in Normal (Z) Direction
2.1.2. Acceleration in X (or Y) Direction
Beams Along the X Direction
Beams Along the Y Direction
Proof-Mass
2.2. Output and Sensitivity
2.3. Modeling Dynamic Behavior
2.3.1. Natural Frequency
2.3.2. Amplitude Frequency Characteristics
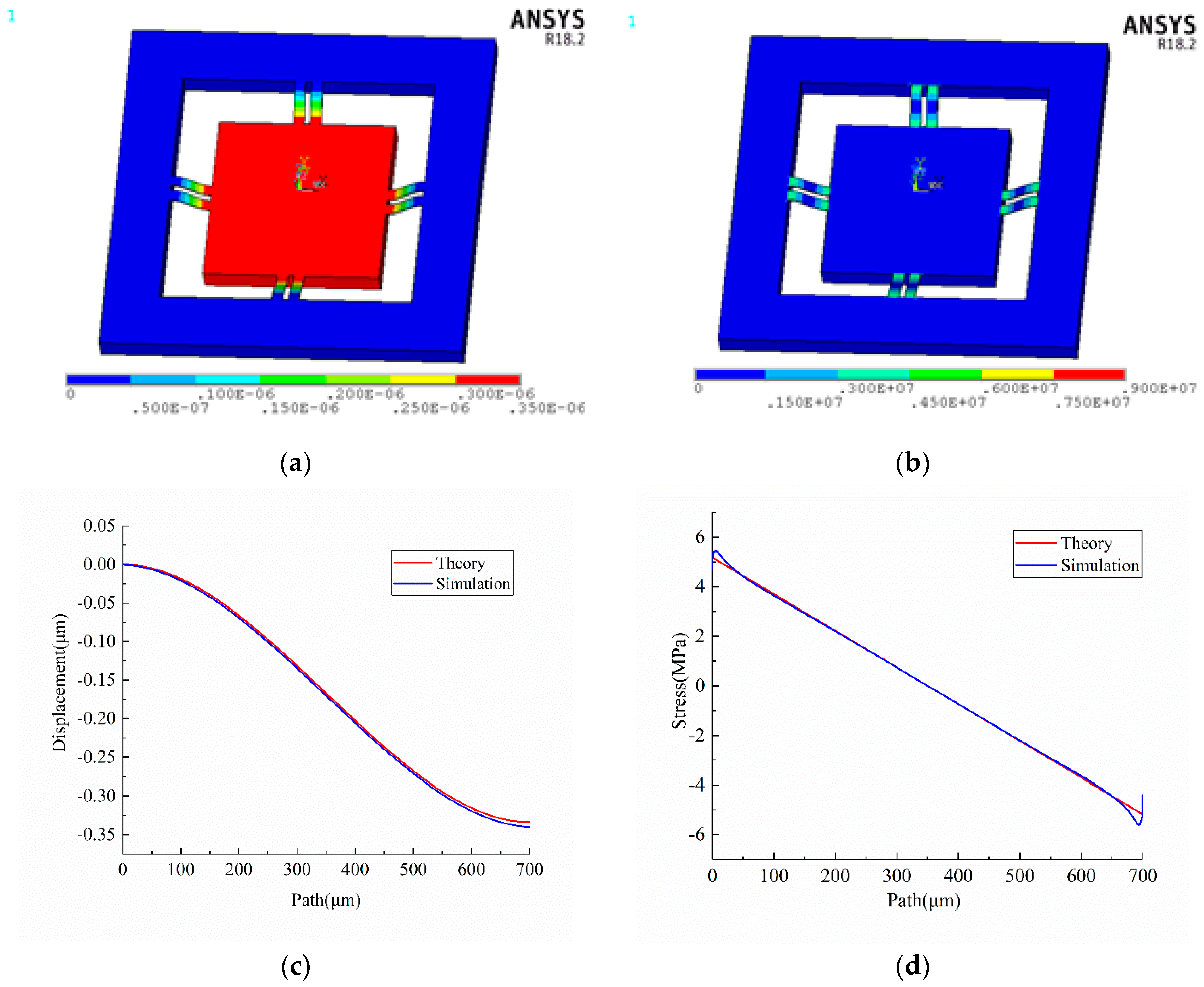
3. Mechanical Simulation
3.1. Static Simulation
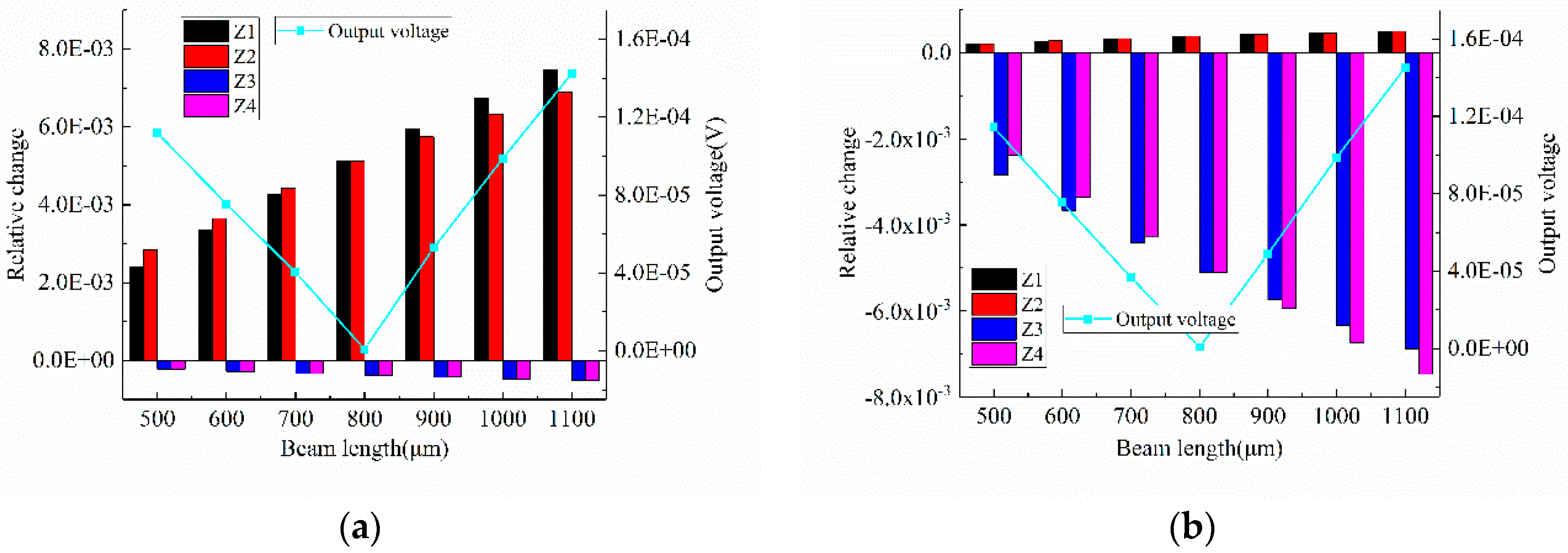
3.1.1. Acceleration in Normal (Z) Direction
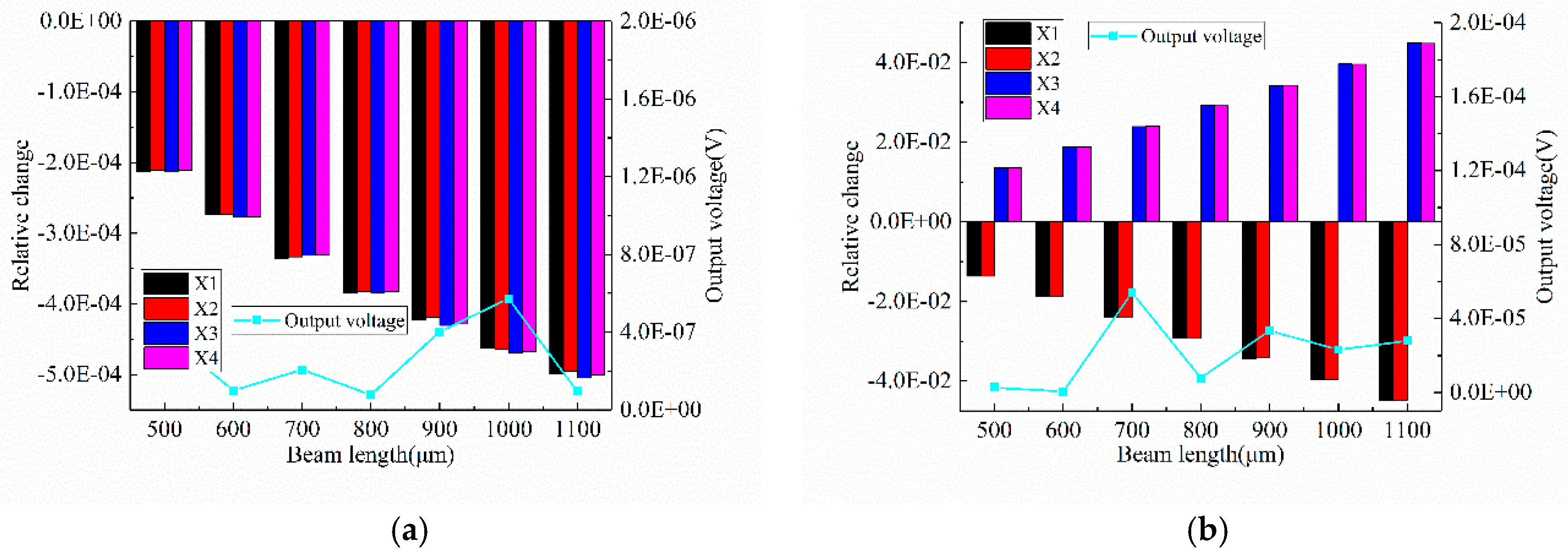
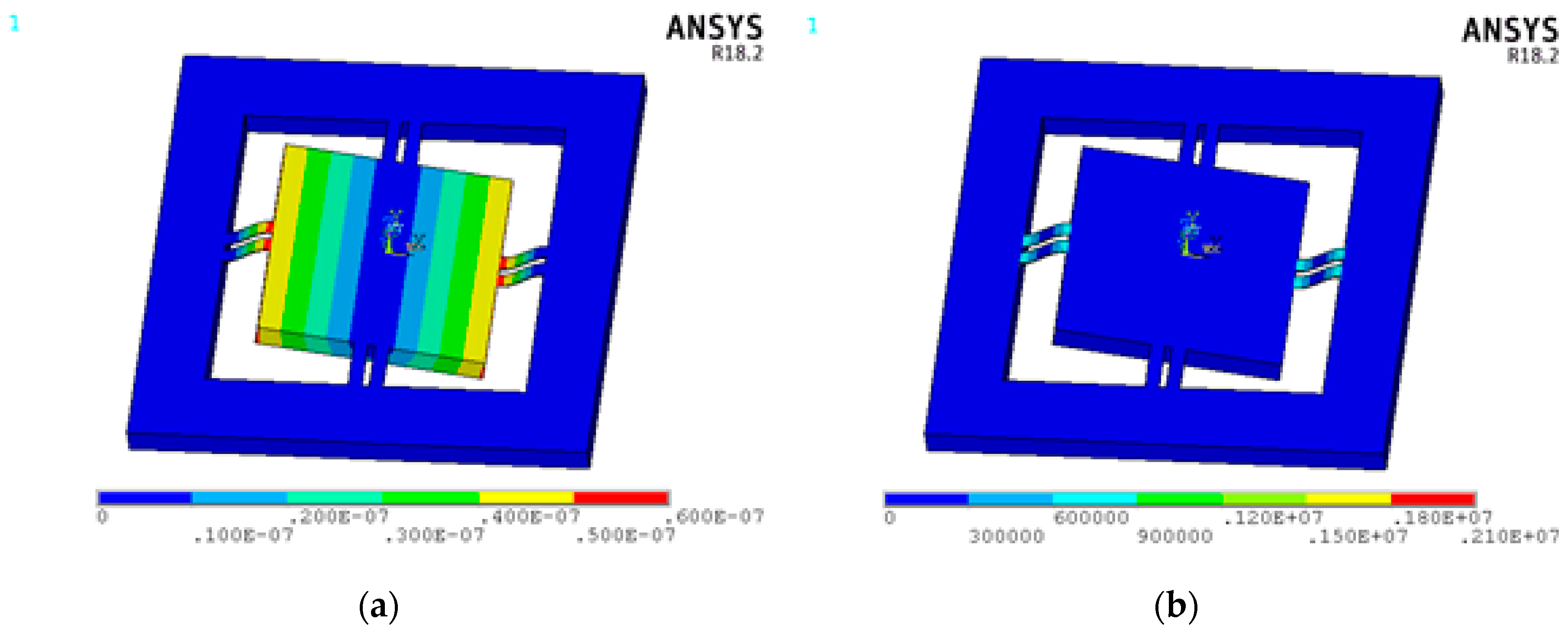
3.1.2. Acceleration in the X Direction
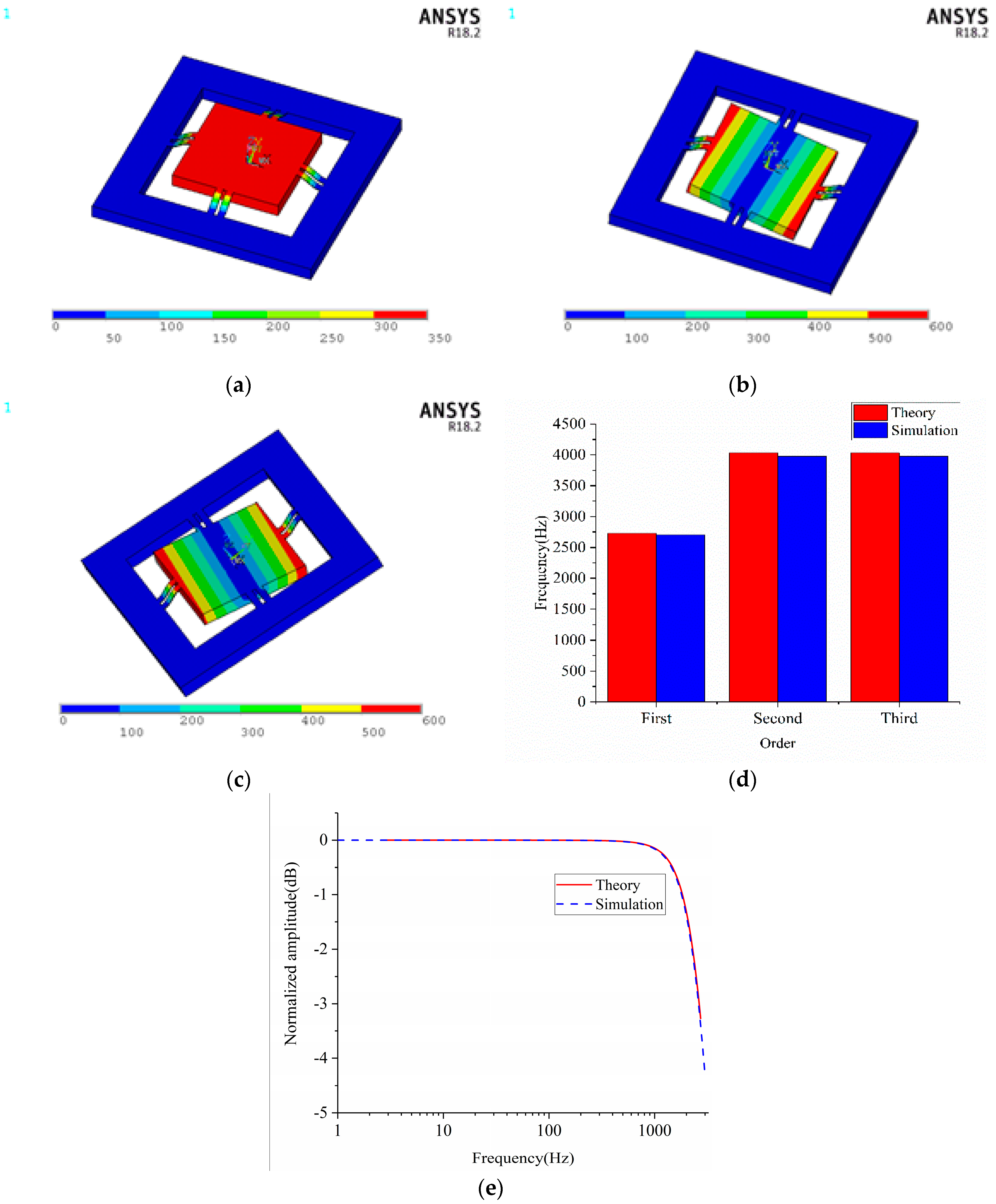
3.2. Natural Frequency and Frequency Characteristic
4. Results
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Parameters | Value (μm) | Parameters | Value (μm) |
|---|---|---|---|
| beam length | 500–1100 | beam width | 200 |
| beam thickness | 15 | beam distance | 300 |
| Proof mass length | 3200 | Proof mass thickness | 380 |
| Piezo-resistors length | 96 | Piezo-resistors width | 8 |
References
- Biswas, S.; Gogoi, A.K. Design Issues of Piezoresistive MEMS Accelerometer for an Application Specific Medical Diagnostic System. IETE Tech. Rev. 2016, 33, 11–16. [Google Scholar] [CrossRef]
- Sabato, A.; Niezrecki, C.; Fortino, G. Wireless MEMS-Based Accelerometer Sensor Boards for Structural Vibration Monitoring: A Review. IEEE Sens. J. 2016, 17, 226–235. [Google Scholar] [CrossRef]
- Speller, K.E.; Yu, D. A low-noise MEMS accelerometer for unattended ground sensor applications. Proc. SPIE 2004, 5417, 63–72. [Google Scholar]
- Chiang, C.T. Design of a CMOS MEMS Accelerometer Used in IoT Devices for Seismic Detection. IEEE J. Emerg. Sel. Top. Circuits Syst. 2018, 8, 566–577. [Google Scholar] [CrossRef]
- O’Loughlin, C.D.; Gaudin, C.; Morton, J.P.; White, D.J. MEMS accelerometers for measuring dynamic penetration events in geotechnical centrifuge tests. Int. J. Phys. Model. Geotech. 2015, 14, 31–39. [Google Scholar] [CrossRef]
- Santoso, D.R.; Maryanto, S.; Nadhir, A.J.T. Application of Single MEMS-accelerometer to Measure 3-axis Vibrations and 2-axis Tilt-Angle Simultaneously. TELKOMNIKA Telecommun. Comput. Electron. Control 2015, 13, 442–450. [Google Scholar] [CrossRef]
- Sankar, A.R.; Das, S.; Lahiri, S.K. Cross-axis sensitivity reduction of a silicon MEMS piezoresistive accelerometer. Microsyst. Technol. 2009, 15, 511–518. [Google Scholar] [CrossRef]
- Raaja, B.P.; Daniel, R.J.; Sumangala, K. A Simple Analytical Model for MEMS Cantilever Beam Piezoelectric Accelerometer and High Sensitivity Design for SHM (structural health monitoring) Applications. Trans. Electr. Electron. Mater. 2017, 18, 78–88. [Google Scholar] [CrossRef] [Green Version]
- Dutta, S.; Saxena, P.; Panchal, A.; Pal, R.; Jain, K.K.; Bhattacharya, D.K. Effect of vacuum packaging on bandwidth of push–pull type capacitive accelerometer structure. Microsyst. Technol. 2018, 6, 1–8. [Google Scholar] [CrossRef]
- Roylance, L.M.; Angell, J.B. A batch-fabricated silicon accelerometer. IEEE Trans. Electron Devices 2005, 26, 1911–1917. [Google Scholar] [CrossRef]
- Jung, H.I.; Kwon, D.S.; Kim, J.J.M.; Letters, N.S. Fabrication and characterization of monolithic piezoresistive high-g three-axis accelerometer. Micro Nano Syste. Lett. 2017, 5. [Google Scholar] [CrossRef]
- Zhao, S.; Shi, Y.; Zhao, Y.; Sun, Y.; Ren, J.; Li, F. Design of a Piezoresistive Accelerometer Sensor with Low Transverse Effect. Micronanoelectron. Technol. 2018, 55, 577–582. [Google Scholar]
- Yu, X.; Zhao, L.; Jiang, Z.; Ding, J.; Peng, N.; Zhao, Y.J.S. A Novel Piezoresistive Accelerometer with SPBs to Improve the Tradeoff between the Sensitivity and the Resonant Frequency. Sensors 2016, 16, 210. [Google Scholar] [Green Version]
- Liu, X.R.; Shi, K.L.; Zou, J.L. Multi-Objective Optimization Design for Piezoresistive Accelerometer. In Proceedings of the International Conference of the Chinese Society of Micro-Nano Technology, Beijing, China, 28–31 July 2016; pp. 321–326. [Google Scholar]
- Van Kampen, R.P.; Wolffenbuttel, R.F. Modeling the mechanical behavior of bulk-micromachined silicon accelerometers. Sens. Actuators A Phys. 1998, 64, 137–150. [Google Scholar] [CrossRef]
- Mukhiya, R.; Gopal, R.; Pant, B.D.; Khanna, V.K.; Bhattacharyya, T.K. Design, modeling and FEM-based simulations of a 1-DoF MEMS bulk micromachined piezoresistive accelerometer. Microsyst. Technol. 2015, 21, 2241–2258. [Google Scholar] [CrossRef]
- Lin, L.; Pan, F.; Xu, J.; Guo, H. Design of a three-axis high-g piezoresistive accelerometer. In Proceedings of the IEEE International Conference on Nano/micro Engineered and Molecular Systems, Xiamen, China, 20–23 January 2010; pp. 773–776. [Google Scholar]
- Wang, W.; Hao, Y. Design and anslysis of a two-end fixed beam structure of piezoresistive accelerometer. Trans. Microsyst. Technol. 2003, 22, 30–32. [Google Scholar]
- Meng, M.Y.; Liu, J.; Shi, Y.B. Structure mechanics analysis on three-axis piezoresistive micro accelerometer. J. Chin. Inert. Technol. 2007, 15, 355–358. [Google Scholar]
- Wang, P.; Zhao, Y.; Tian, B.; Liu, Y.; Wang, Z.; Li, C.; Zhao, Y. A piezoresistive micro-accelerometer with high frequency response and low transverse effect. Meas. Sci. Technol. 2017, 28, 015103. [Google Scholar] [CrossRef]
- Hang, B.T.; Tan, T.D.; Duc, T.C. Three-axis piezoresistive accelerometer with adjustable axial resolutions. Vietnam J. Mech. 2012, 34, 45–54. [Google Scholar] [CrossRef]
- Doll, J.C.; Pruitt, B.L. Piezoresistor Design and Applications; Springer: New York, NY, USA, 2013. [Google Scholar]
- Plaza, J.A.; Esteve, J.; Cané, C.J.S. Twin-mass accelerometer optimization to reduce the package stresses. Sens. Actuators A Phys. 2000, 80, 199–207. [Google Scholar] [CrossRef]
- Bian, Y.M.; Zheng, F.; He, H.T. Research on damping characteristics of MEMS piezoresistive accelerometer. Micronanoelectron. Micronanoelectron. Technol. 2008, 45, 466–469. [Google Scholar]
- Meng, L.F.; Zheng, B. Sensor Principle and Technology; National Defense Industry Press: Beijing, China, 2005. [Google Scholar]







| Parameters | Piezoelectric | Piezo-Resistive | Capacitive |
|---|---|---|---|
| DC response | poor | good | good |
| Impedance | high | low | high |
| Signal level | high | low | medium |
| Static Calibration | poor | good | good |
| sensitivity | high | low | high |
| Damped design | poor | good | good |
| Cost | high | low | high |
| Measurement of long course impact (>10 ms) | bad | good | good |
| Sensitivity to installation and other stresses | high | low | low |
| Circuit | simple | simple | complex |
| Work | Stress | Displacement | Sensitivity | Cross-Axis Sensitivity | Natural Frequency | Amplitude Frequency Characteristics | DoF |
|---|---|---|---|---|---|---|---|
| Kampen et al. [15] | √ a | √ | √ | √ | √ | × b | 1 |
| Mukhiya et al. [16] | √ | √ | √ | √ | √ | × | 1 |
| Yu et al. [13] | √ | × | × | × | √ | × | 1 |
| Lin et al. [17] | √ | √ | √ | × | √ | × | 3 |
| Wang et al. [18] | √ | × | √ | √ | × | 1 | |
| Meng et al. [19] | √ | √ | × | × | √ | × | 3 |
| Wang et al. [20]. | √ | √ | × | × | √ | × | 1 |
| Hang et al. [21] | × | × | × | × | × | √ | 3 |
| Liu et al. [8] | √ | √ | √ | × | √ | √ | 1 |
| This work | √ | √ | √ | √ | √ | √ | 3 |
| Piezo-Resistors | Induced Stress | |
|---|---|---|
| X1 | compressive | |
| X2 | tensile | |
| X3 | tensile | |
| X4 | compressive | |
| Y1 | compressive | |
| Y2 | compressive | |
| Y3 | compressive | |
| Y4 | compressive | |
| Z1 | compressive | |
| Z2 | compressive | |
| Z3 | tensile | |
| Z4 | tensile |
| Piezo-Resistors | Induced Stress | |
|---|---|---|
| X1 | tensile | |
| X2 | tensile | |
| X3 | compressive | |
| X4 | compressive | |
| Y1 | tensile | |
| Y2 | tensile | |
| Y3 | compressive | |
| Y4 | compressive | |
| Z1 | compressive | |
| Z2 | tensile | |
| Z3 | tensile | |
| Z4 | compressive |
| Parameters | Description (μm) |
|---|---|
| beam length/l | 700 |
| beam width/w | 200 |
| beam thickness/t | 15 |
| beam distance/db | 100 |
| proof-mass length/a | 3200 |
| proof-mass width/a | 3200 |
| proof-mass thickness/h | 380 |
| frame length/lf | 6600 |
| frame width/wf | 1000 |
| frame thickness/tf | 395 |
| Parameters | Theory | Simulation |
|---|---|---|
| Sensitivity (SZZ) (mV/g) | 1.196 | 1.177 |
| Cross-axis sensitivity (SXZ) (mV/g) | 0 | −6.526 × 10−4 |
| Cross-axis sensitivity (SYZ) (mV/g) | 0 | 2.287 × 10−4 |
| Parameters | Theory | Simulation |
|---|---|---|
| Sensitivity (SXX) (mV/g) | 0.226 | 0.212 |
| Cross-axis sensitivity (SYX) (mV/g) | 0 | 7.140 × 10−6 |
| Cross-axis sensitivity (SZX) (mV/g) | −0.003 | −0.001 |
| Sensitivity (mV/g) | Acceleration Direction | ||
|---|---|---|---|
| X | Y | Z | |
| X | 0.209 | 0.003 | 0.009 |
| Y | 0.004 | 0.212 | 0.003 |
| Z | 0.011 | 0.014 | 1.247 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; He, C.; Wang, R.; Xue, C.; Zhang, W. A Mathematical Model of a Piezo-Resistive Eight-Beam Three-Axis Accelerometer with Simulation and Experimental Validation. Sensors 2018, 18, 3641. https://doi.org/10.3390/s18113641
Song J, He C, Wang R, Xue C, Zhang W. A Mathematical Model of a Piezo-Resistive Eight-Beam Three-Axis Accelerometer with Simulation and Experimental Validation. Sensors. 2018; 18(11):3641. https://doi.org/10.3390/s18113641
Chicago/Turabian StyleSong, Jinlong, Changde He, Renxin Wang, Chenyang Xue, and Wendong Zhang. 2018. "A Mathematical Model of a Piezo-Resistive Eight-Beam Three-Axis Accelerometer with Simulation and Experimental Validation" Sensors 18, no. 11: 3641. https://doi.org/10.3390/s18113641
APA StyleSong, J., He, C., Wang, R., Xue, C., & Zhang, W. (2018). A Mathematical Model of a Piezo-Resistive Eight-Beam Three-Axis Accelerometer with Simulation and Experimental Validation. Sensors, 18(11), 3641. https://doi.org/10.3390/s18113641






