Hierarchical Sub-Pixel Anomaly Detection Framework for Hyperspectral Imagery
Abstract
:1. Introduction
2. Related Work and Proposed Method
2.1. Brief Introduction to the RX Algorithm
2.2. Hierarchical-RX Algorithm
| Algorithm 1 Hierarchical-RX Algorithm |
| Input and Initialization: 1. Spectral matrix , target spectrum , set tolerance , , |
| Hierarchical Background Spectral Restraint: 2. 3. 4. Rebuild data 5. |
| Stop Criterion: 6. ; if , go back to step 2; else, go to step 7 Anomaly Regularization: 7. |
| Output: 8. Final outputs: . |
3. Theoretical Analysis
3.1. Background Spectral Suppression Layer
- (1)
- The output of the H-RX algorithm will be restrained to a small constant for the background spectrum, whereas this constant will generally retain the original value for the anomaly target spectrum.
- (2)
- This layer can increase the difference between the target spectrum and background spectrum.
- (3)
- Because the background spectrum is restrained to a zero vector, the sparsity of the rebuilt data will be significantly increased.
- (4)
- Although the H-RX algorithm contains several RX detectors, as the data sparsity increases, the calculation speed of each layer with the exception of the first layer will increase.
3.2. Stop Criteria Layer
- (1)
- The background spectral magnitude is reduced while its direction in the spectral space is maintained, and after several ranges of suppression operations, it will be transformed close to a zero vector.
- (2)
- Concurrently, the target spectra remain unchanged.
3.3. Spatial Regularization Layer Analysis
4. Experimental Results and Analysis
4.1. Dataset Description
4.2. Performance Analysis of Background Suppression Layer
4.3. Sub-Pixel Anomaly Detection Experiments
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mo, C.; Kim, G.; Lim, J.; Kim, M.S.; Cho, H.; Cho, B.K. Detection of Lettuce Discoloration Using Hyperspectral Reflectance Imaging. Sensors 2015, 15, 29511–29534. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lacar, F.M.; Lewis, M.M.; Grierson, I.T. Use of hyperspectral imagery for mapping grape varieties in the Barossa Valley, South Australia. In Proceedings of the International Geoscience and Remote Sensing Symposium, Scanning the Present and Resolving the Future, Sydney, Australia, 9–13 July 2001; Volume 6, pp. 2875–2877. [Google Scholar]
- Meer, F.V.D. Analysis of spectral absorption features in hyperspectral imagery. Int. J. Appl. Earth Obs. Geoinf. 2004, 5, 55–68. [Google Scholar] [CrossRef]
- Malthus, T.; Mumby, P. Remote sensing of the coastal zone: An overview and priorities for future research. Int. J. Remote Sens. 2003, 24, 2805–2815. [Google Scholar] [CrossRef] [Green Version]
- Han, Y.; Li, J.; Zhang, Y.; Hong, Z.; Wang, J. Sea Ice Detection Based on an Improved Similarity Measurement Method Using Hyperspectral Data. Sensors 2017, 17, 1124. [Google Scholar] [Green Version]
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral Remote Sensing Data Analysis and Future Challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef] [Green Version]
- Matteoli, S.; Diani, M.; Corsini, G. A tutorial overview of anomaly detection in hyperspectral images. Aerosp. Electron. Syst. Mag. 2010, 25, 5–28. [Google Scholar] [CrossRef]
- Reed, I.S.; Yu, X. Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1760–1770. [Google Scholar] [CrossRef]
- Wright, J.; Ganesh, A.; Rao, S.; Ma, Y. Robust Principal Component Analysis: Exact Recovery of Corrupted Low-Rank Matrices. In Proceedings of the 23rd Annual Conference on Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 7–10 December 2009. [Google Scholar]
- Xu, Y.; Wu, Z.; Li, J.; Plaza, A.; Wei, Z. Anomaly Detection in Hyperspectral Images Based on Low-Rank and Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1990–2000. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, B.; Zhang, L.; Wang, S. A Low-Rank and Sparse Matrix Decomposition-Based Mahalanobis Distance Method for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1376–1389. [Google Scholar] [CrossRef]
- Borghys, D.; Kåsen, I.; Achard, V.; Perneel, C. Comparative evaluation of hyperspectral anomaly detectors in different types of background. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XVIII; International Society for Optics and Photonics: Bellingham, WA, USA, 2012; 83902J-83902J-12; Volume 8390. [Google Scholar]
- Nasrabadi, N.M. Regularization for spectral matched filter and RX anomaly detector—Art. no. 696604. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery Xiv; Shen, S.S., Lewis, P.E., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2008; Volume 6966, p. 96604. [Google Scholar]
- Kwon, H.; Nasrabadi, N.M. Kernel RX-algorithm: A nonlinear anomaly detector for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 388–397. [Google Scholar] [CrossRef]
- Zhao, C.; Deng, W.; Yan, Y.; Yao, X. Progressive Line Processing of Kernel RX Anomaly Detection Algorithm for Hyperspectral Imagery. Sensors 2017, 17, 1815. [Google Scholar] [CrossRef] [PubMed]
- Williams, J.P.; Bihl, T.J.; Bauer, K.W. Towards the mitigation of correlation effects in anomaly detection for hyperspectral imagery. J. Defense Model. Simul. 2013, 10, 263–273. [Google Scholar] [CrossRef]
- Williams, J.; Bihl, T.; Bauer, K. Mitigation of Correlation and Heterogeneity Effects in Hyperspectral Data. Intell. Eng. Syst. Through Artif. Neural Netw. 2010, 20, 501–507. [Google Scholar]
- Gao, C.; Meng, D.; Yang, Y.; Wang, Y.; Zhou, X.; Hauptmann, A.G. Infrared Patch-Image Model for Small Target Detection in a Single Image. IEEE Trans. Image Process. 2013, 22, 4996–5009. [Google Scholar] [CrossRef] [PubMed]
- Anderson, K.L.; Iltis, R.A. A tracking algorithm for infrared images based on reduced sufficient statistics. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 464–472. [Google Scholar] [CrossRef]
- Xiong, Y.; Peng, J.X.; Ding, M.Y.; Xue, D.H. An extended track-before-detect algorithm for infrared target detection. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 1087–1092. [Google Scholar] [CrossRef]
- Manolakis, D.; Marden, D.; Shaw, G.A. Hyperspectral Image Processing for Automatic Target Detection Applications. Linc. Lab. J. 2003, 14, 79–116. [Google Scholar]
- Chang, C.I. Multiparameter Receiver Operating Characteristic Analysis for Signal Detection and Classification. IEEE Sens. J. 2010, 10, 423–442. [Google Scholar] [CrossRef]
- Clare, P.E.; Bernhardt, M.; Oxford, W.J. A new approach to anomaly detection in hyperspectral images. Proc. SPIE 2003, 5093, 17–28. [Google Scholar]
- Rakotomamonjy, A. Optimizing area under ROC curve with SVMs. In Proceedings of the 1th International Workshop on ROC Analysis in Artificial Intelligence (ROCAI), Valencia, Spain, 22 August 2004; pp. 71–80. [Google Scholar]
- Green, R.O.; Chrien, T.G.; Enmark, H.T. First Results from the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS). Remote Sens. Environ. 1987, 65, 127–143. [Google Scholar]
- Porter, W.M.; Enmark, H.T. A System Overview of the Airborne Visible/Infrared Imaging Spectrometer (Aviris). Proc. SPIE 1988, 834, 22–31. [Google Scholar]
- Mitchell, P.A. Hyperspectral digital imagery collection experiment (HYDICE). In Proceedings of the Geographic Information Systems, Photogrammetry, and Geological/Geophysical Remote Sensing, Paris, France, 25–28 September 1995; Volume 2587, pp. 70–95. [Google Scholar]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image processing system (SIPS)-interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–463. [Google Scholar] [CrossRef]
- Rao, N.R.; Garg, P.K.; Ghosh, S.K. Development of an agricultural crops spectral library and classification of crops at cultivar level using hyperspectral data. Precis. Agric. 2007, 8, 173–185. [Google Scholar] [CrossRef]
- Nidamanuri, R.R.; Zbell, B. A method for selecting optimal spectral resolution and comparison metric for material mapping by spectral library search. Progr. Phys. Geogr. 2010, 34, 47–58. [Google Scholar] [CrossRef]
- Keshava, N. Distance metrics and band selection in hyperspectral processing with applications to material identification and spectral libraries. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1552–1565. [Google Scholar] [CrossRef]
- Stefanou, M.S.; Kerekes, J.P. A Method for Assessing Spectral Image Utility. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1698–1706. [Google Scholar] [CrossRef] [Green Version]
- Ren, H.; Chang, C.; Rand, R.S. How to design synthetic images to validate and evaluate hyperspectral imaging algorithms. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XIV; International Society for Optics and Photonics: Bellingham, WA, USA, 2008; Volume 6966. [Google Scholar]
- Bioucas-Dias, J.M. A variable splitting augmented Lagrangian approach to linear spectral unmixing. In Proceedings of the 2009 Workshop on Hyperspectral Image & Signal Processing: Evolution in Remote Sensing, Grenoble, France, 26–28 August 2009; pp. 1–4. [Google Scholar]
- Chen, S.Y.; Wang, Y.; Wu, C.C.; Liu, C. Real-time causal processing of anomaly detection for hyperspectral imagery. Aerosp. Electron. Syst. IEEE Trans. 2014, 50, 1511–1534. [Google Scholar] [CrossRef]




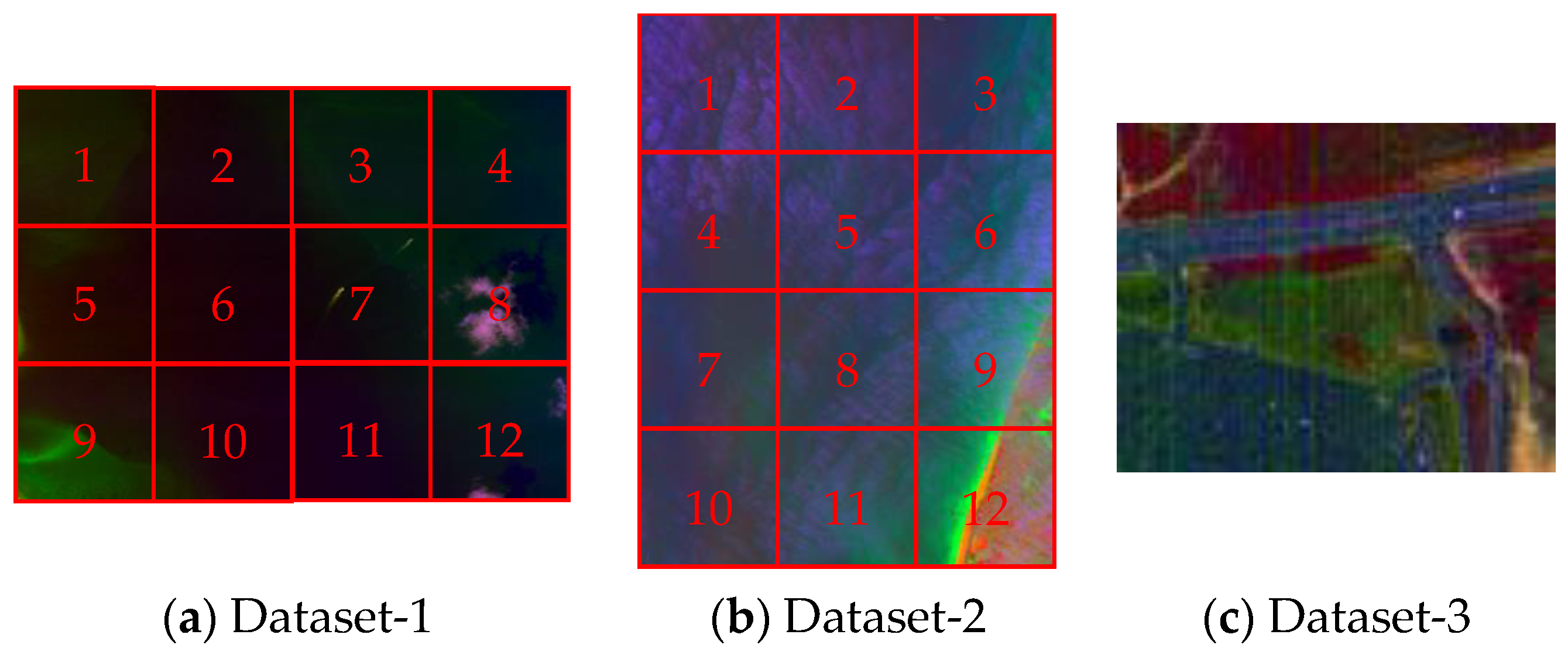









| Dataset | Size | Bands | Resolution | Sub-Pixel Targets | Background |
|---|---|---|---|---|---|
| AVIRIS Dataset-1 | 224 | 15.5 m | Synthetic | Real-World | |
| AVIRIS Dataset-2 | 224 | 15.5 m | Synthetic | Real-World | |
| HYDICE Dataset-3 | 162 | 1 m | Real | Real-World |
| Algorithm | Original RX | Suppression-Once | Suppression-Twice |
|---|---|---|---|
| Distance | 1.9 | 6.8 | 125.58 |
| Test Data | Euclidean Distance | SAM |
|---|---|---|
| Original data | 0.0595 | |
| Rebuilt data after first layer | 0.2073 | |
| Rebuilt data after second layer | 0.9619 |
| Dataset | Number of Iterations | Spatial Smooth Window |
|---|---|---|
| Dataset-1 | 2 | |
| Dataset-2 | 2 | |
| Dataset-3 | 1 |
| Algorithm | Dataset-1 (%) | Dataset-2 (%) | Dataset-3 (%) | |||
|---|---|---|---|---|---|---|
| P-D | P-FA | P-D | P-FA | P-D | P-FA | |
| Original RX | 72.3 ± 12.5 | 16.7 ± 7.6 | 53.7 ± 18.2 | 99.1 ± 2.6 | 76.8 ± 0.01 | 26.3 ± 0.01 |
| RPCA | 85.9 ± 9.2 | 9.7 ± 6.2 | 62.3 ± 24.8 | 100.0 ± 0.0 | 76.7 ± 0.00 | 17.8 ± 0.01 |
| Kernel RX | 85.0 ± 14.0 | 61.5 ± 45.64 | 29.2 ± 28.7 | 68.4 ± 22.9 | 61.3 ± 0.01 | 84.6 ± 0.02 |
| LARSR | 54.9 ± 31.9 | 81.6 ± 38.6 | 17.9 ± 35.2 | 95.2 ± 12.1 | 82.6 ± 0.01 | 26.9 ± 0.01 |
| Proposed | 89.1 ± 7.8 | 11.5 ± 7.5 | 65.4 ± 21.7 | 94.1 ± 12.9 | 83.4 ± 0.00 | 12.6 ± 0.00 |
| Algorithm | Dataset-2 (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| Original RX | 79.9 | 87.9 | 80.7 | 90.9 | 80.6 | 77.4 | 87.1 | 78.7 | 49.6 | 85.8 | 85.6 | 30.8 |
| RPCA | 54.0 | 77.7 | 74.9 | 74.9 | 74.4 | 19.6 | 79.8 | 70.0 | 0.0 | 74.7 | 78.8 | 0.0 |
| Kernel RX | 70.0 | 84.6 | 83.5 | 90.4 | 81.5 | 67.1 | 88.4 | 87.9 | 61.2 | 86.3 | 84.3 | 50.8 |
| LARSR | 50.8 | 65.9 | 46.9 | 56.3 | 55.8 | 54.8 | 73.5 | 57.9 | 63.0 | 99.4 | 56.6 | 47.0 |
| Proposed | 94.7 | 94.9 | 88.0 | 89.8 | 94.9 | 89.6 | 89.5 | 90.0 | 84.4 | 95.0 | 95.0 | 54.5 |
| Algorithm | Dataset-2 (s) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| Original RX | 4.8 | 4.8 | 4.3 | 4.7 | 4.8 | 4.6 | 4.7 | 4.2 | 4.8 | 4.3 | 4.8 | 4.6 |
| RPCA | 70.7 | 57.7 | 56.6 | 121.2 | 59.0 | 48.4 | 73.7 | 62.1 | 100.4 | 56.9 | 58.8 | 157.9 |
| Kernel RX | 755.35 | 818.68 | 1087.3 | 2962.91 | 811.7 | 876.6 | 1521.7 | 919.2 | 768.4 | 1478.9 | 683.5 | 801.1 |
| LARSR | 9.1 | 9.9 | 9.9 | 11.6 | 9.7 | 7.9 | 10.6 | 8.7 | 7.9 | 6.3 | 10.3 | 6.8 |
| Proposed | 5.7 | 5.3 | 4.8 | 5.4 | 5.3 | 5.4 | 5.2 | 4.7 | 5.3 | 4.7 | 5.2 | 5.2 |
| Algorithm | AUC Score (%) | ||
|---|---|---|---|
| Dataset-1 | Dataset-2 | Dataset-3 | |
| Original RX | 92.70 ± 2.2 | 76.25 ± 17.79 | 96.98 ± 0.01 |
| RPCA | 96.58 ± 1.8 | 56.57 ± 31.27 | 97.42 ± 0.01 |
| Kernel RX | 92.81 ± 6.6 | 78.01 ± 12.69 | 94.21 ± 0.01 |
| LARSR | 46.29 ± 30.6 | 60.66 ± 14.37 | 96.62 ± 0.00 |
| Proposed | 97.71 ± 1.7 | 88.36 ± 11.22 | 98.39 ± 0.00 |
| Algorithm | Average Time Consumption (s) | ||
|---|---|---|---|
| Dataset-1 | Dataset-2 | Dataset-3 | |
| Original RX | 0.79 ± 0.02 | 4.61 ± 0.23 | 0.88 ± 0.04 |
| RPCA | 51.08 ± 5.90 | 76.96 ± 33.01 | 139.11 ± 1.61 |
| Kernel RX | 13.34 ± 5.81 | 1123.26 ± 641.14 | 83.96 ± 1.17 |
| LARSR | 1.61 ± 0.37 | 9.06 ± 1.59 | 3.08 ± 0.29 |
| Proposed | 1.29 ± 0.11 | 6.17 ± 0.31 | 1.25 ± 0.13 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Zhao, B.; Feng, F.; Nan, J.; Li, C. Hierarchical Sub-Pixel Anomaly Detection Framework for Hyperspectral Imagery. Sensors 2018, 18, 3662. https://doi.org/10.3390/s18113662
Wang W, Zhao B, Feng F, Nan J, Li C. Hierarchical Sub-Pixel Anomaly Detection Framework for Hyperspectral Imagery. Sensors. 2018; 18(11):3662. https://doi.org/10.3390/s18113662
Chicago/Turabian StyleWang, Wenzheng, Baojun Zhao, Fan Feng, Jinghong Nan, and Cheng Li. 2018. "Hierarchical Sub-Pixel Anomaly Detection Framework for Hyperspectral Imagery" Sensors 18, no. 11: 3662. https://doi.org/10.3390/s18113662
APA StyleWang, W., Zhao, B., Feng, F., Nan, J., & Li, C. (2018). Hierarchical Sub-Pixel Anomaly Detection Framework for Hyperspectral Imagery. Sensors, 18(11), 3662. https://doi.org/10.3390/s18113662





