A Method for Extrinsic Parameter Calibration of Rotating Binocular Stereo Vision Using a Single Feature Point
Abstract
:1. Introduction
2. Principles and Methods
2.1. Camera model of the Binocular Stereo Vision
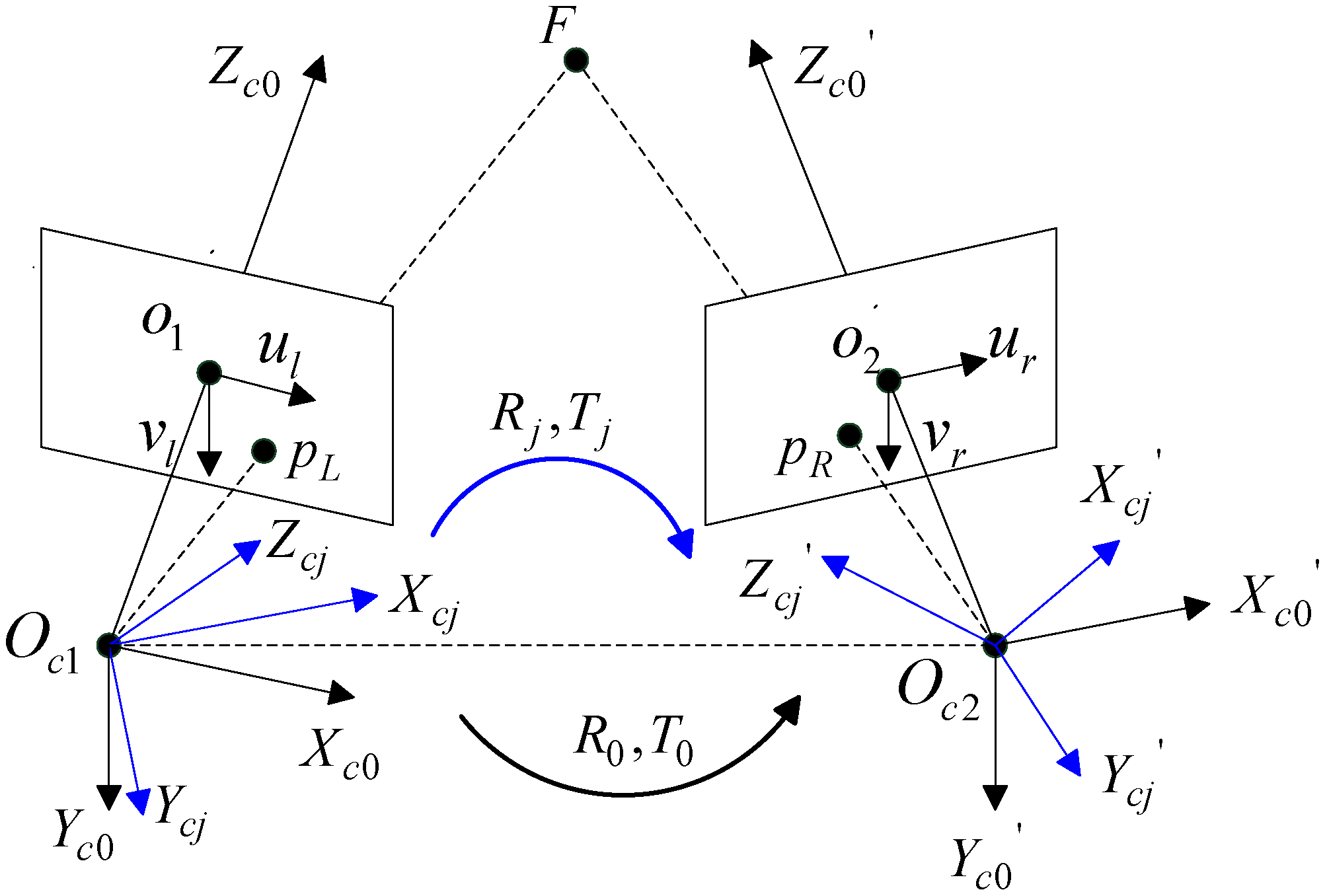
2.2. Extrinsic Parameter Calibration Using a Single Feature Point
3. Feasibility Analysis
4. Experiments
4.1. Computer Simulation
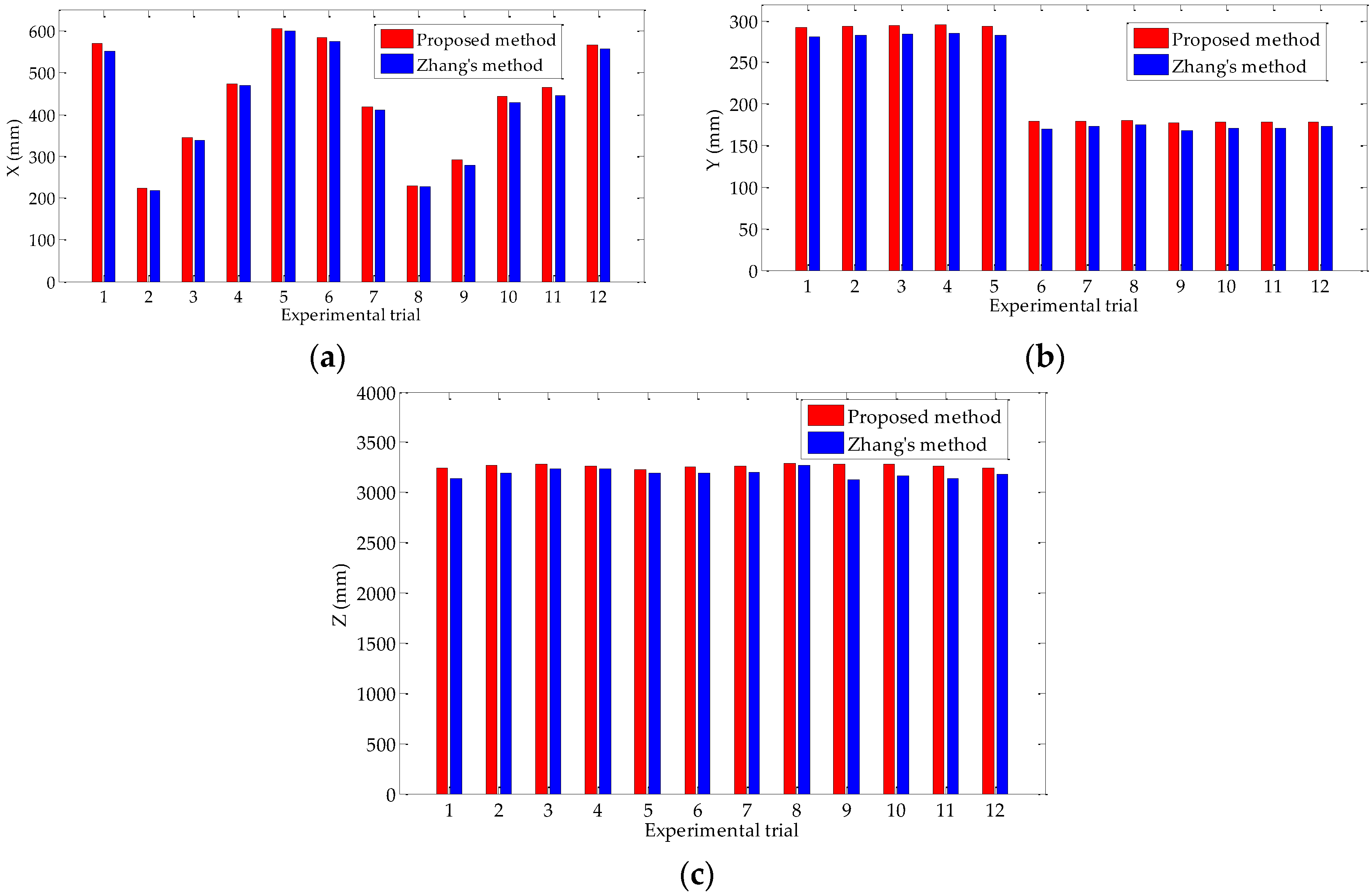
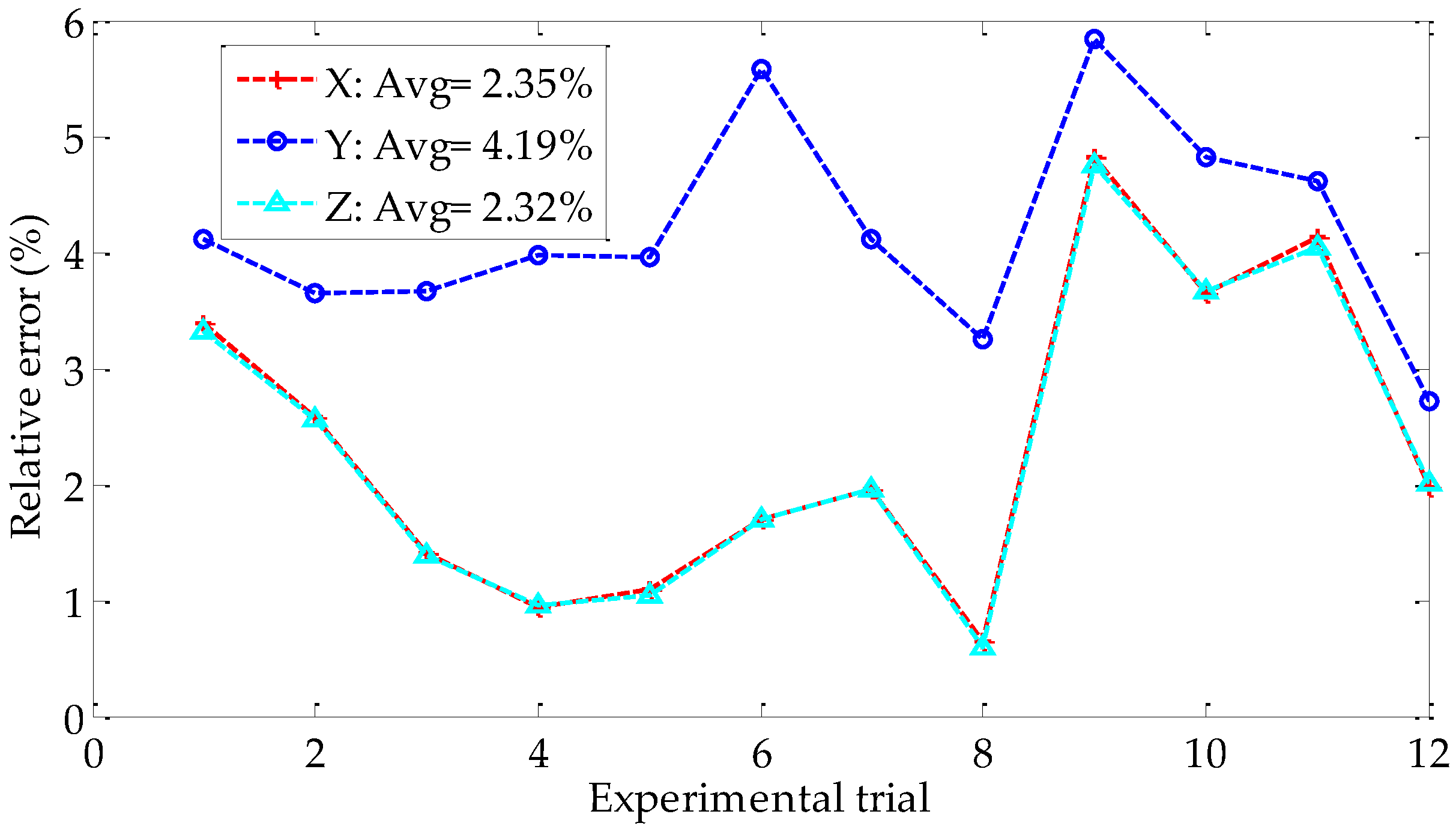
4.2. Physical Experiment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tsai, R.; Lenz, R.K. A technique for fully autonomous and efficient 3D robotics hand/eye calibration. IEEE Trans. Robot. Autom. 1989, 5, 345–358. [Google Scholar] [CrossRef]
- Tsai, R.Y. An efficient and accurate camera calibration technique for 3D machine vision. In Proceedings of the CVPR’86: IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Miami Beach, FL, USA, 22–26 June 1986; pp. 364–374. [Google Scholar]
- Tian, S.-X.; Lu, S.; Liu, Z.-M. Levenberg-Marquardt algorithm based nonlinear optimization of camera calibration for relative measurement. In Proceedings of the 34th Chinese Control Conference, Hangzhou, China, 28–30 July 2015; pp. 4868–4872. [Google Scholar]
- Habed, A.; Boufama, B. Camera self-calibration from bivariate polynomials derived from Kruppa’s equations. Pattern Recognit. 2008, 41, 2484–2492. [Google Scholar] [CrossRef]
- Wang, L.; Kang, S.-B.; Shum, H.-Y.; Xu, G.-Y. Error analysis of pure rotation based self-calibration. In Proceedings of the Eighth IEEE International Conference on Computer Vision, Vancouver, BC, Canada, 7–14 July 2001; pp. 464–471. [Google Scholar]
- Hemayed, E.E. A survey of camera calibration. In Proceedings of the IEEE Conference on Advanced Video and Signal Based Surveillance, Miami, FL, USA, 21–22 July 2003; pp. 351–357. [Google Scholar]
- Abdel-Aziz, Y.I.; Karara, H.M. Direct linear transformation into object space coordinates in close-range photogrammetry. Photogramm. Eng. Remote Sens. 2015, 81, 103–107. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, D. Automatic calibration of computer vision based on RAC calibration algorithm. Metall. Min. Ind. 2015, 7, 308–312. [Google Scholar]
- Zhang, Z. Flexible camera calibration by viewing a plane from unknown orientations. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; pp. 666–673. [Google Scholar]
- Martins, H.A.; Birk, J.R.; Kelley, R.B. Camera models based on data from two calibration planes. Comput. Graph. Image Process. 1981, 17, 173–180. [Google Scholar] [CrossRef]
- Faugeras, O.D.; Luong, Q.-T.; Maybank, S.J. Camera self-calibration: Theory and experiments. In Proceedings of the 2nd European Conference on Computer Vision, Santa Margherita Ligure, Italy, 19–22 May 1992; pp. 321–334. [Google Scholar]
- Li, X.; Zheng, N.; Cheng, H. Camera linear self-calibration method based on the Kruppa equation. J. Xi'an Jiaotong Univ. 2003, 37, 820–823. [Google Scholar]
- Hartley, R. Euclidean reconstruction and invariants from multiple images. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 1036–1041. [Google Scholar] [CrossRef]
- Triggs, B. Auto-calibration and the absolute quadric. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, PR, USA, 17–19 June 1997; pp. 609–614. [Google Scholar]
- De Ma, S. A self-calibration technique for active vision system. IEEE Trans. Robot. Autom. 1996, 12, 114–120. [Google Scholar] [CrossRef]
- Zhang, Z.; Tang, Q. Camera self-calibration based on multiple view images. In Proceedings of the Nicograph International (NicoInt), Hanzhou, China, 6–8 July 2016; pp. 88–91. [Google Scholar]
- Wu, Z.; Radke, R.J. Keeping a pan-tilt-zoom camera calibrated. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1994–2007. [Google Scholar] [CrossRef] [PubMed]
- Junejo, I.N.; Foroosh, H. Optimizing PTZ camera calibration from two images. Mach. Vis. Appl. 2012, 23, 375–389. [Google Scholar] [CrossRef]
- Echigo, T. A camera calibration technique using three sets of parallel lines. Mach. Vis. Appl. 1990, 3, 159–167. [Google Scholar] [CrossRef]
- Song, K.-T.; Tai, J.-C. Dynamic calibration of Pan-Tilt-Zoom cameras for traffic monitoring. IEEE Trans. Syst. Man Cybern. Part B 2006, 36, 1091–1103. [Google Scholar] [CrossRef]
- Schoepflin, T.N.; Dailey, D.J. Dynamic camera calibration of roadside traffic management cameras for vehicle speed estimation. IEEE Trans. Intell. Transp. Syst. 2003, 4, 90–98. [Google Scholar] [CrossRef]
- Kim, H.; Hong, K.S. A practical self-calibration method of rotating and zooming cameras. In Proceedings of the 15th International Conference on Pattern Recognition, Barcelona, Spain, 3–7 September 2000; pp. 354–357. [Google Scholar]
- Rodríguez, J.A.M. Online self-camera orientation based on laser metrology and computer algorithms. Opt. Commun. 2011, 284, 5601–5612. [Google Scholar] [CrossRef]
- Rodríguez, J.A.M.; Alanís, F.C.M. Binocular self-calibration performed via adaptive genetic algorithm based on laser line imaging. J. Mod. Opt. 2016, 63, 1219–1232. [Google Scholar] [CrossRef]
- Ji, Q.; Dai, S. Self-calibration of a rotating camera with a translational offset. IEEE Trans. Robot. Autom. 2004, 20, 1–14. [Google Scholar] [CrossRef]
- Cai, H.; Zhu, W.; Li, K.; Liu, M. A linear camera self-calibration approach from four points. In Proceedings of the 4th International Symposium on Computational Intelligence and Design, Hangzhou, China, 28–30 October 2011; pp. 202–205. [Google Scholar]
- Tang, A.W.K.; Hung, Y.S. A Self-calibration algorithm based on a unified framework for constraints on multiple views. J. Math. Imaging Vis. 2012, 44, 432–448. [Google Scholar] [CrossRef]
- Yu, H.; Wang, Y. An improved self-calibration method for active stereo camera. In Proceedings of the Sixth World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; pp. 5186–5190. [Google Scholar]
- De Agapito, L.; Hartley, R.I.; Hayman, E. Linear self-calibration of a rotating and zooming camera. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Fort Collins, CO, USA, 23–25 June 1999; pp. 15–21. [Google Scholar]
- Sun, J.; Wang, P.; Qin, Z.; Qiao, H. Effective self-calibration for camera parameters and hand-eye geometry based on two feature points motions. IEEE/CAA J. Autom. Sin. 2017, 4, 370–380. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, F.; Little, J.J. A two-point method for PTZ camera calibration in sports. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 287–295. [Google Scholar]











| Camera | fu/pixels | fv/pixels | u0/pixels | v0/pixels | kc |
|---|---|---|---|---|---|
| Left | 2493.09 | 2493.92 | 725.77 | 393.03 | [−0.17, 0.18, 0.003, 0.0004, 0.00] |
| Right | 2811.56 | 2811.54 | 692.04 | 371.96 | [−0.13, 0.16, 0.001, 0.0003, 0.00] |
| om | [0.01085, 0.05695, 0.03387] | ||||
| T0/mm | [−306.9049, −4.3956, 39.6172] | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, X.; Wan, Z.; Zhang, J. A Method for Extrinsic Parameter Calibration of Rotating Binocular Stereo Vision Using a Single Feature Point. Sensors 2018, 18, 3666. https://doi.org/10.3390/s18113666
Wang Y, Wang X, Wan Z, Zhang J. A Method for Extrinsic Parameter Calibration of Rotating Binocular Stereo Vision Using a Single Feature Point. Sensors. 2018; 18(11):3666. https://doi.org/10.3390/s18113666
Chicago/Turabian StyleWang, Yue, Xiangjun Wang, Zijing Wan, and Jiahao Zhang. 2018. "A Method for Extrinsic Parameter Calibration of Rotating Binocular Stereo Vision Using a Single Feature Point" Sensors 18, no. 11: 3666. https://doi.org/10.3390/s18113666
APA StyleWang, Y., Wang, X., Wan, Z., & Zhang, J. (2018). A Method for Extrinsic Parameter Calibration of Rotating Binocular Stereo Vision Using a Single Feature Point. Sensors, 18(11), 3666. https://doi.org/10.3390/s18113666





