Silicon Field Effect Transistor as the Nonlinear Detector for Terahertz Autocorellators
Abstract
1. Introduction
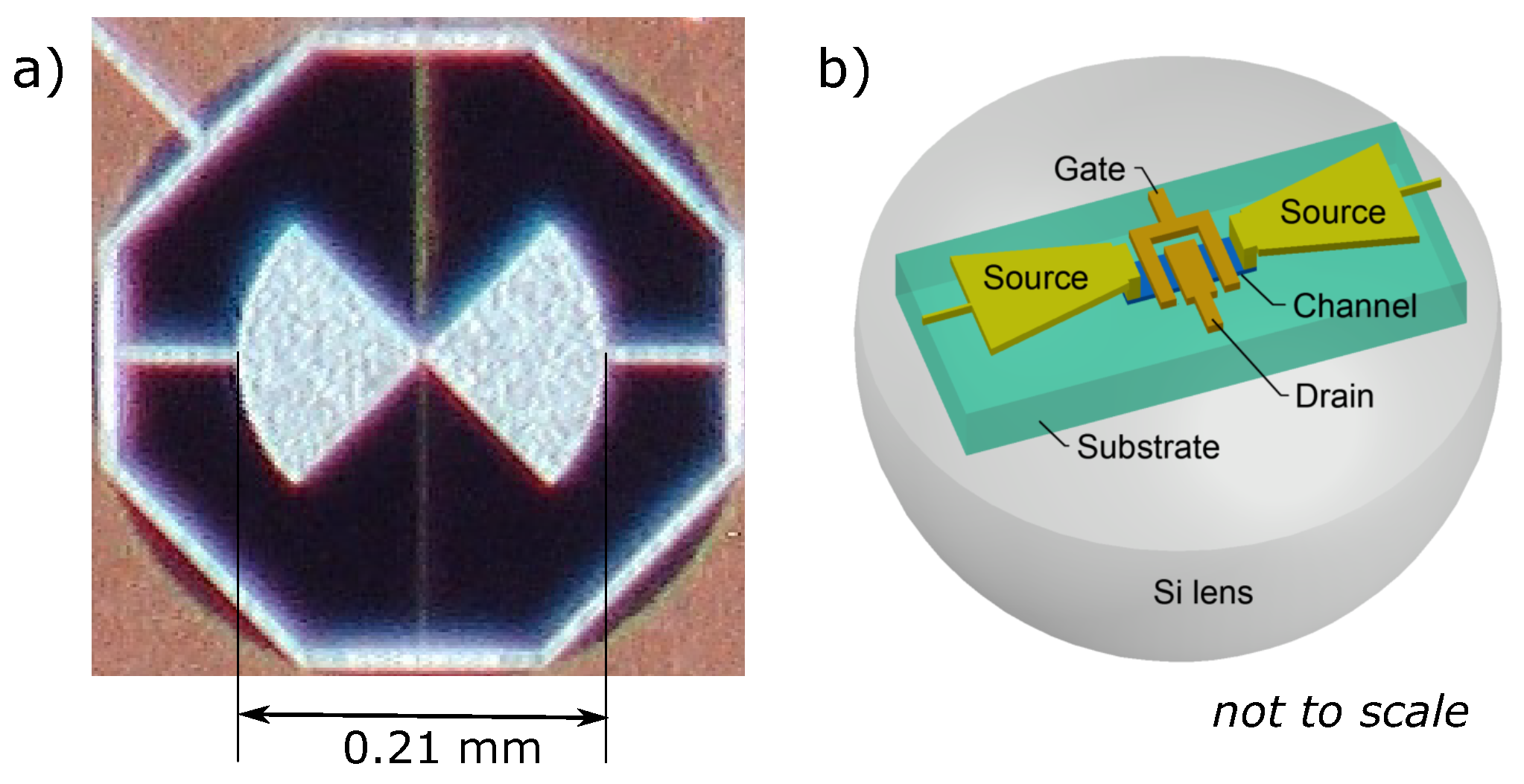
2. Si CMOS FET Detector
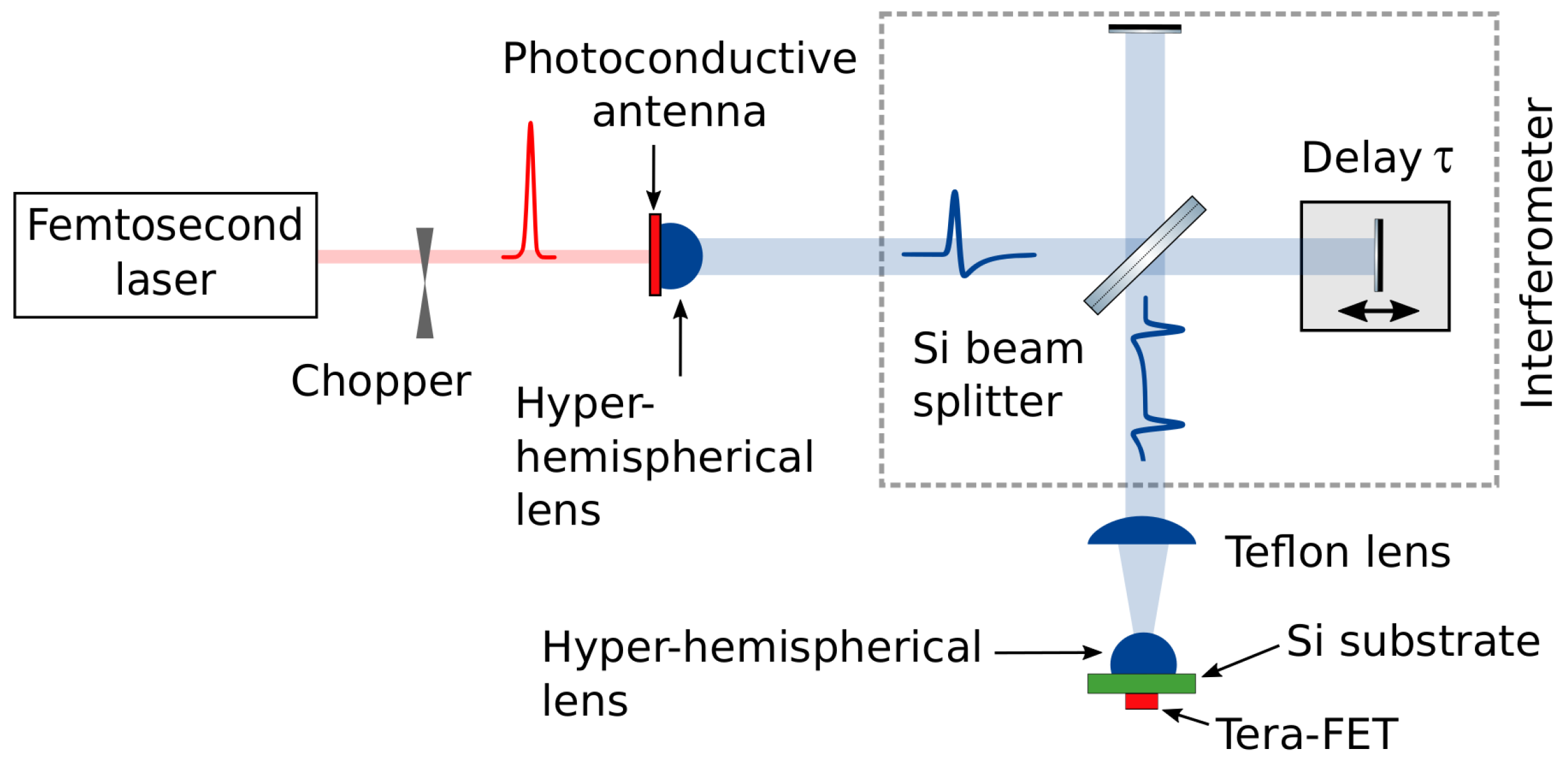
3. Experiment Setup
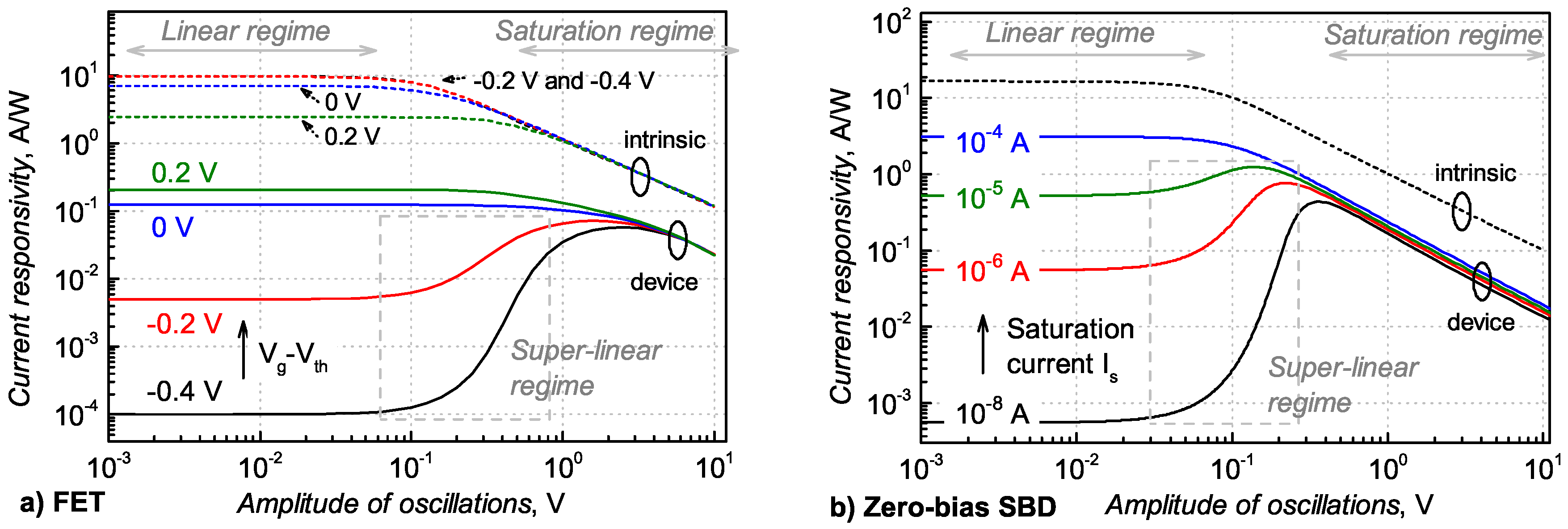
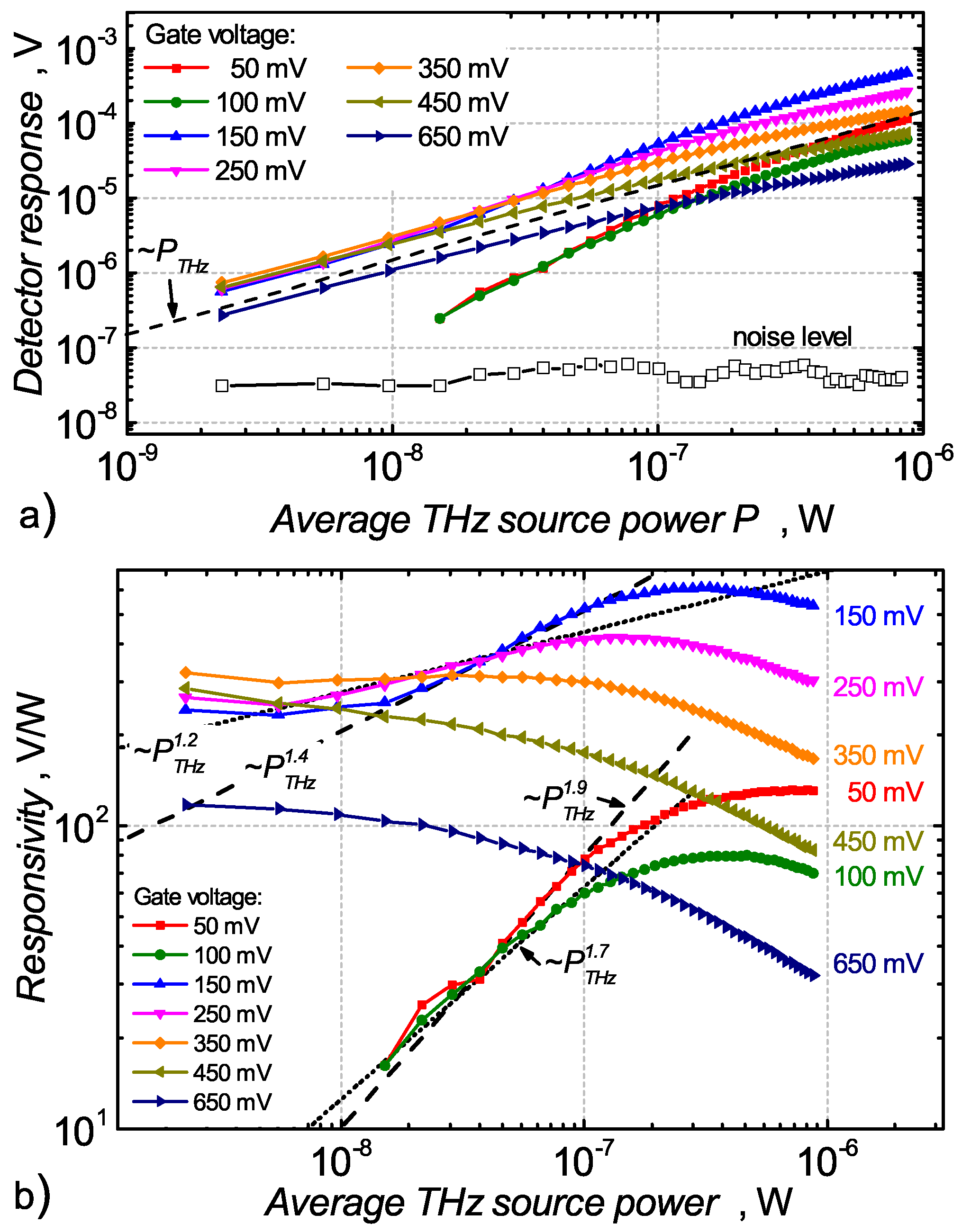
4. Nonlinearity of the TeraFET Detector
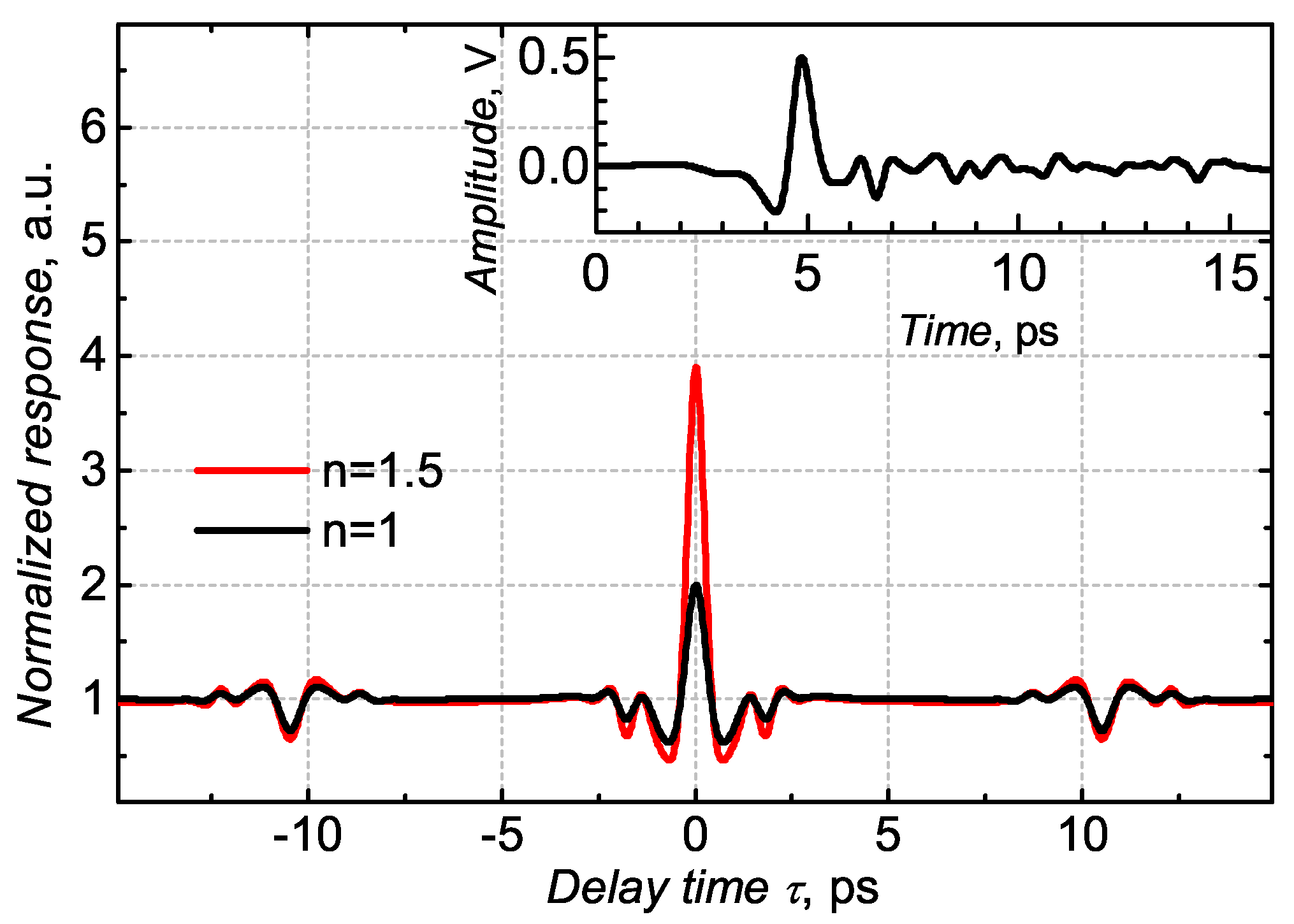
5. Nonlinear Autocorrelation Measurements
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schneider, H.; Drachenko, O.; Winnerl, S.; Helm, M.; Walther, M. Quadratic autocorrelation of free-electron laser radiation and photocurrent saturation in two-photon quantum well infrared photodetectors. Appl. Phys. Lett. 2006, 89, 133508. [Google Scholar] [CrossRef]
- Jepsen, P.; Cooke, D.; Koch, M. Terahertz spectroscopy and imaging—Modern techniques and applications. Laser Photon. Rev. 2011, 5, 124–166. [Google Scholar] [CrossRef]
- Schneider, H.; Drachenko, O.; Winnerl, S.; Helm, M.; Maier, T.; Walther, M. Autocorrelation measurements of free-electron laser radiation using a two-photon QWIP. Infrared Phys. Technol. 2007, 50, 95–99. [Google Scholar] [CrossRef]
- Preu, S.; Mittendorff, M.; Winnerl, S.; Cojocari, O.; Penirschke, A. THz Autocorrelators for ps Pulse Characterization Based on Schottky Diodes and Rectifying Field-Effect Transistors. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 922–929. [Google Scholar] [CrossRef]
- Mittendorff, M.; Winnerl, S.; Kamann, J.; Eroms, J.; Weiss, D.; Schneider, H.; Helm, M. Ultrafast graphene-based broadband THz detector. Appl. Phys. Lett. 2013, 103, 021113. [Google Scholar] [CrossRef]
- Lisauskas, A.; Ikamas, K.; Massabeau, S.; Bauer, M.; Čibiraitė, D.; Matukas, J.; Mangeney, J.; Mittendorff, M.; Winnerl, S.; Krozer, V.; et al. Field-effect transistors as electrically controllable nonlinear rectifiers for the characterization of terahertz pulses. APL Photon. 2018, 3, 051705. [Google Scholar] [CrossRef]
- Peter, F.; Winnerl, S.; Nitsche, S.; Dreyhaupt, A.; Schneider, H.; Helm, M. Coherent terahertz detection with a large-area photoconductive antenna. Appl. Phys. Lett. 2007, 91, 081109. [Google Scholar] [CrossRef]
- Mittendorff, M.; Xu, M.; Dietz, R.J.B.; Künzel, H.; Sartorius, B.; Schneider, H.; Helm, M.; Winnerl, S. Large area photoconductive terahertz emitter for 1.55 μm excitation based on an InGaAs heterostructure. Nanotechnology 2013, 24, 214007. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Mu, K.; Zhou, Y.; Wang, H.; Zhang, C.; Zhang, X.C. High-power THz to IR emission by femtosecond laser irradiation of random 2D metallic nanostructures. Sci. Rep. 2015, 5, 12536. [Google Scholar] [CrossRef] [PubMed]
- Farzad Zangeneh-Nejad, R.S. Significant enhancement in the efficiency of photoconductive antennas using a hybrid graphene molybdenum disulphide structure. J. Nanophoton. 2016, 10, 036005. [Google Scholar] [CrossRef]
- Lee, Y.S. Principles of Terahertz Science and Technology; Springer US: Boston, MA, USA, 2009. [Google Scholar]
- Hale, P.J.; Madeo, J.; Chin, C.; Dhillon, S.S.; Mangeney, J.; Tignon, J.; Dani, K.M. 20 THz broadband generation using semi-insulating GaAs interdigitated photoconductive antennas. Opt. Express 2014, 22, 26358. [Google Scholar] [CrossRef] [PubMed]
- Dreyhaupt, A.; Winnerl, S.; Dekorsy, T.; Helm, M. High-intensity terahertz radiation from a microstructured large-area photoconductor. Appl. Phys. Lett. 2005, 86, 121114. [Google Scholar] [CrossRef]
- Liu, T.A.; Tani, M.; Nakajima, M.; Hangyo, M.; Pan, C.L. Ultrabroadband terahertz field detection by photoconductive antennas based on multi-energy arsenic-ion-implanted GaAs and semi-insulating GaAs. Appl. Phys. Lett. 2003, 83, 1322–1324. [Google Scholar] [CrossRef]
- Krotkus, A.; Bertulis, K.; Adomavičius, R.; Pačebutas, V.; Geižutis, A. Semiconductor Materials for Ultrafast Optoelectronic Applications. Lith. J. Phys. 2009, 49, 359–372. [Google Scholar] [CrossRef]
- Duvillaret, L.; Garet, F.; Roux, J.; Coutaz, J. Analytical modeling and optimization of terahertz time-domain spectroscopy experiments, using photoswitches as antennas. IEEE J. Sel. Top. Quantum Electron. 2001, 7, 615–623. [Google Scholar] [CrossRef]
- Lisauskas, A.; Pfeiffer, U.; Öjefors, E.; Bolìvar, P.H.; Glaab, D.; Roskos, H.G. Rational design of high-responsivity detectors of terahertz radiation based on distributed self-mixing in silicon field-effect transistors. J. Appl. Phys. 2009, 105, 114511. [Google Scholar] [CrossRef]
- Boppel, S.; Lisauskas, A.; Mundt, M.; Seliuta, D.; Minkevicius, L.; Kasalynas, I.; Valusis, G.; Mittendorff, M.; Winnerl, S.; Krozer, V.; et al. CMOS Integrated Antenna-Coupled Field-Effect Transistors for the Detection of Radiation From 0.2 to 4.3 THz. IEEE Trans. Microw. Theory Tech. 2012, 60, 3834–3843. [Google Scholar] [CrossRef]
- Lisauskas, A.; Boppel, S.; Mundt, M.; Krozer, V.; Roskos, H.G. Subharmonic Mixing With Field-Effect Transistors: Theory and Experiment at 639 GHz High Above T. IEEE Sens. J. 2013, 13, 124–132. [Google Scholar] [CrossRef]
- Čibiraitė, D.; Bauer, M.; Rämer, A.; Chevtchenko, S.; Lisauskas, A.; Matukas, J.; Krozer, V.; Heinrich, W.; Roskos, H.G. Enhanced performance of AlGaN/GaN HEMT-Based THz detectors at room temperature and at low temperature. In Proceedings of the 42nd Intenational Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Cancun, Mexico, 27 August–1 September 2017; pp. 1–2. [Google Scholar]
- Ikamas, K.; Cibiraite, D.; Lisauskas, A.; Bauer, M.; Krozer, V.; Roskos, H.G. Broadband Terahertz Power Detectors Based on 90-Nm Silicon CMOS Transistors with Flat Responsivity up to 2.2 THz. IEEE Electron. Device Lett. 2018, 39, 1413–1416. [Google Scholar] [CrossRef]
- Dyakonov, M.; Shur, M. Detection, mixing, and frequency multiplication of terahertzradiation by two-dimensional electronic fluid. IEEE Trans. Electron. Dev. 1996, 43, 380–387. [Google Scholar] [CrossRef]
- Knap, W.; Dyakonov, M.; Coquillat, D.; Teppe, F.; Dyakonova, N.; Lusakowski, J.; Karpierz, K.; Sakowicz, M.; Valušis, G.; Seliuta, D. Field effect transistors for terahertz detection: Physics and first imaging applications. J. Infrared Millim. Terahertz Waves 2009, 30, 1319–1337. [Google Scholar] [CrossRef]
- Preu, S.; Lu, H.; Sherwin, M.S.; Gossard, A.C. Detection of nanosecond-scale, high power THz pulses with a field effect transistor. Rev. Sci. Instrum. 2012, 83, 053101. [Google Scholar] [CrossRef] [PubMed]
- Sakhno, M.; Golenkov, A.; Sizov, F. Uncooled detector challenges: Millimeter-wave and terahertz long channel field effect transistor and Schottky barrier diode detectors. J. Appl. Phys. 2013, 114, 164503. [Google Scholar] [CrossRef]
- Bauer, M.; Rämer, A.; Boppel, S.; Chevtchenko, S.; Lisauskas, A.; Heinrich, W.; Krozer, V.; Roskos, H.G. High-sensitivity wideband THz detectors based on GaN HEMTs with integrated bow-tie antennas. In Proceedings of the 10th European Microwave Integrated Circuits Conference (EuMIC), Paris, France, 7–8 September 2015; pp. 1–4. [Google Scholar]
- Takagi, S.; Toriumi, A.; Iwase, M.; Tango, H. On the universality of inversion layer mobility in Si MOSFET’s: Part I—Effects of substrate impurity concentration. IEEE Trans. Electron. Devices 1994, 41, 2357–2362. [Google Scholar] [CrossRef]
- Carpintero, G.; Garcia-Munoz, E.; Hartnagel, H.; Preu, S.; Räisänen, A. Semiconductor TeraHertz Technology: Devices and Systems at Room Temperature Operation; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Dyakonov, M.; Shur, M. Detection, mixing, and frequency multiplication of terahertz radiation by two-dimensional electronic fluid. IEEE Trans. Electron. Devices 1996, 43, 380–387. [Google Scholar] [CrossRef]
- Preu, S.; Kim, S.; Verma, R.; Burke, P.G.; Sherwin, M.S.; Gossard, A.C. An improved model for non-resonant terahertz detection in field-effect transistors. J. Appl. Phys. 2012, 111, 024502. [Google Scholar] [CrossRef]
- Khmyrova, I.; Seijyou, Y. Analysis of plasma oscillations in high-electron mobility transistorlike structures: Distributed circuit approach. Appl. Phys. Lett. 2007, 91, 143515. [Google Scholar] [CrossRef]
- Lisauskas, A.; Bauer, M.; Ramer, A.; Ikamas, K.; Matukas, J.; Chevtchenko, S.; Heinrich, W.; Krozer, V.; Roskos, H.G. Terahertz rectification by plasmons and hot carriers in gated 2D electron gases. In Proceedings of the 41st Intenational Conference on Noise and Fluctuations (ICNF), Xi’an, China, 2–6 June 2015; pp. 1–5. [Google Scholar]
- Gutin, A.; Kachorovskii, V.; Muraviev, A.; Shur, M. Plasmonic terahertz detector response at high intensities. J. Appl. Phys. 2012, 112, 014508. [Google Scholar] [CrossRef]
- Rudin, S.; Rupper, G.; Gutin, A.; Shur, M. Theory and measurement of plasmonic terahertz detector response to large signals. J. Appl. Phys. 2014, 115, 064503. [Google Scholar] [CrossRef]
- Dyakonova, N.; Faltermeier, P.; But, D.B.; Coquillat, D.; Ganichev, S.D.; Knap, W.; Szkudlarek, K.; Cywinski, G. Saturation of photoresponse to intense THz radiation in AlGaN/GaN HEMT detector. J. Appl. Phys. 2016, 120, 164507. [Google Scholar] [CrossRef]
- Brown, E.R.; Sung, S.; Grundfest, W.S.; Taylor, Z.D. THz impulse radar for biomedical sensing: nonlinear system behavior. Proc. SPIE 2014, 8941, 89411E. [Google Scholar]
- Shur, M.; Fjeldly, T.A.; Ytterdal, T.; Lee, K. Unified MOSFET model. Solid State Electron. 1992, 35, 1795–1802. [Google Scholar] [CrossRef]
- Franke, C. Zwei-Photonen-Übergänge und Intersubbanddynamik in Halbleiterquantenfilmen. Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, 2011. [Google Scholar]
- Paschotta, R. Encyclopedia of Laser Physics and Technology—Autocorrelators, Pulse Duration, Measurement. Available online: www.rp-photonics.com/autocorrelators.html (accessed on 4 May 2018).
- Krotkus, A. Semiconductors for terahertz photonics applications. J. Phys. D Appl. Phys. 2010, 43, 273001. [Google Scholar] [CrossRef]
- Kroll, J.; Darmo, J.; Unterrainer, K. High-performance terahertz electro-optic detector. Electron. Lett. 2004, 40, 763–764. [Google Scholar] [CrossRef]
- Naftaly, M.; Miles, R. A method for removing etalon oscillations from THz time-domain spectra. Opt. Commun. 2007, 280, 291–295. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ikamas, K.; Nevinskas, I.; Krotkus, A.; Lisauskas, A. Silicon Field Effect Transistor as the Nonlinear Detector for Terahertz Autocorellators. Sensors 2018, 18, 3735. https://doi.org/10.3390/s18113735
Ikamas K, Nevinskas I, Krotkus A, Lisauskas A. Silicon Field Effect Transistor as the Nonlinear Detector for Terahertz Autocorellators. Sensors. 2018; 18(11):3735. https://doi.org/10.3390/s18113735
Chicago/Turabian StyleIkamas, Kęstutis, Ignas Nevinskas, Arūnas Krotkus, and Alvydas Lisauskas. 2018. "Silicon Field Effect Transistor as the Nonlinear Detector for Terahertz Autocorellators" Sensors 18, no. 11: 3735. https://doi.org/10.3390/s18113735
APA StyleIkamas, K., Nevinskas, I., Krotkus, A., & Lisauskas, A. (2018). Silicon Field Effect Transistor as the Nonlinear Detector for Terahertz Autocorellators. Sensors, 18(11), 3735. https://doi.org/10.3390/s18113735




