Combined Channel Estimation with Interference Suppression in CPSS
Abstract
:1. Introduction
2. Signal Model
3. Channel Estimation with Interference Suppression
3.1. Interference Suppression in CIR
3.2. Noise Cancellation in CIR
4. Complexity Analysis and Performance Simulation
4.1. Complexity Analysis
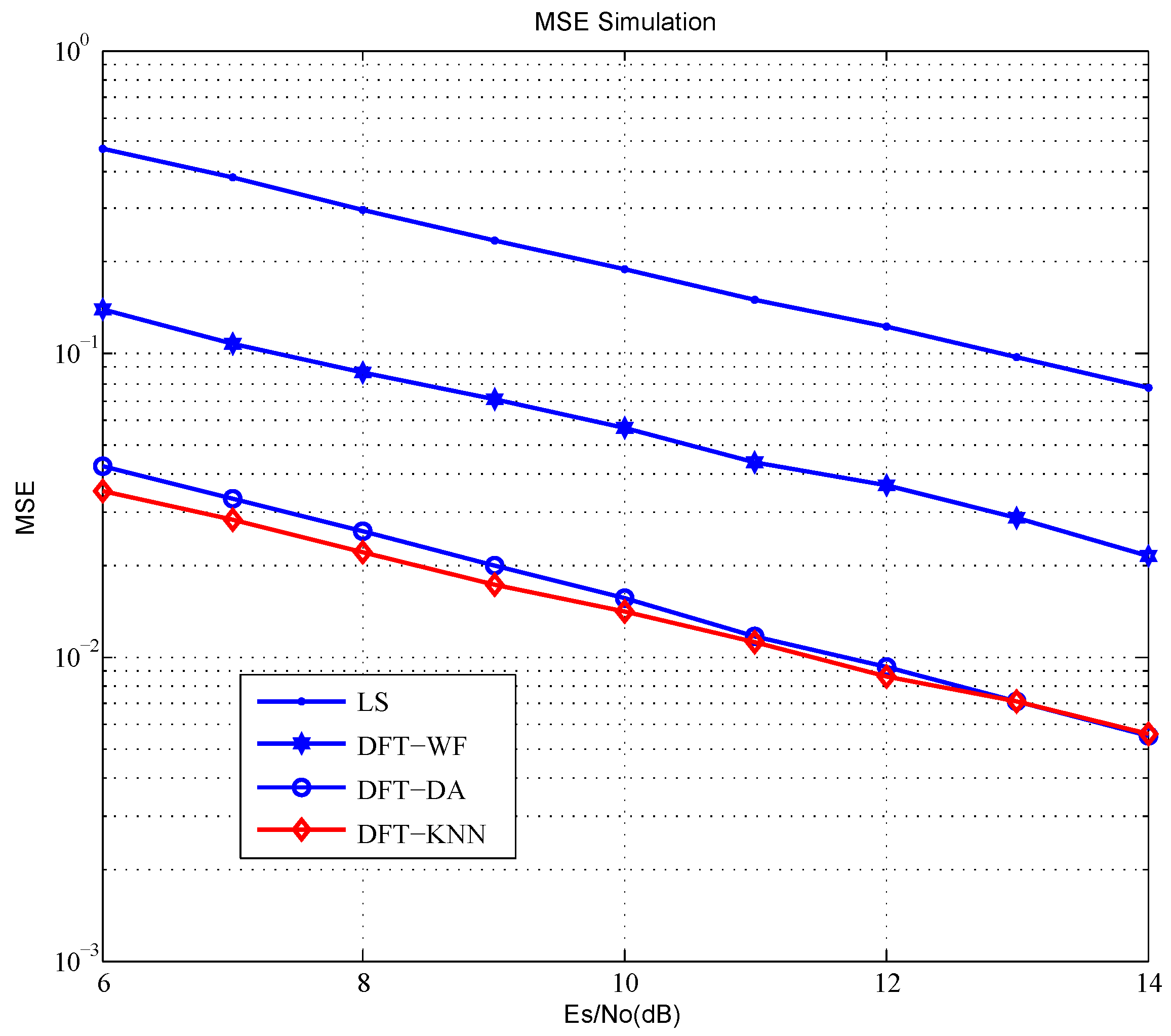
4.2. Simulation Results
4.2.1. Performance without Interference
4.2.2. Performance under Interference
5. Method Application
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Song, H.; Rawat, D.; Jeschke, S.; Brecher, C. Cyber-Physical Systems: Foundations, Principles and Applications; Morgan Kaufmann: Boston, MA, USA, 2016; ISBN 978-0-12-803801-7. [Google Scholar]
- Ning, H.; Liu, H.; Ma, J.; Yang, L.T.; Huang, R. Cyber-physical-social-thinking hyperspace based science and technology. Future Gener. Comput. Syst. 2015, 56, 504–522. [Google Scholar] [CrossRef]
- Jiang, P.; Winkley, J.; Zhao, C.; Munnoch, R.; Min, G.; Yang, L.T. An Intelligent Information Forwarder for Healthcare Big Data Systems with Distributed Wearable Sensors. IEEE Syst. J. 2016, 3, 1147–1159. [Google Scholar] [CrossRef]
- Yi, L.; Deng, X.; Zou, Z.; Ding, D.; Yang, L.T. Confident Information Coverage Hole Detection in Sensor Networks for Uranium Tailing Monitoring. Elsevier J. Parallel Distrib. Comput. 2018, 118, 57–66. [Google Scholar] [CrossRef]
- Naik, V.K.; Liu, C.; Yang, L.T.; Wagner, J. Online resource matching for heterogeneous grid environments. In Proceedings of the IEEE International Symposium on Cluster Computing and the Grid (CCGrid 2005), Cardiff, UK, 9–12 May 2005; pp. 607–614. [Google Scholar]
- Deng, X.; Yang, L.T.; Yi, L.; Wang, M.; Zhu, Z. Detecting Confident Information Coverage Holes in Industrial Internet of Things: An Energy-Efficient Perspective. IEEE Commun. Mag. 2018, 9, 68–73. [Google Scholar] [CrossRef]
- Edfors, O.; Sandell, M.; Van De Beek, J.J.; Wilson, S.K.; Borjesson, P.O. Analysis of DFT-Based Channel Estimators for OFDM. Wirel. Pers. Commun. 2000, 1, 55–70. [Google Scholar] [CrossRef]
- Minn, H.; Dong, I.K.; Bhargava, V.K. A reduced complexity channel estimation for OFDM systems with transmit diversity in mobile wireless channels. IEEE Trans. Commun. 2002, 5, 799–807. [Google Scholar] [CrossRef]
- Fukuhara, T.; Yuan, H.; Takeuchi, Y.; Takeuchi, Y. A novel channel estimation method for OFDM transmission technique under fast time-variant fading channel. In Proceedings of the IEEE Semiannual Vehicular Technology Conference (VTC 2003), Jeju, Korea, 22–25 April 2003; pp. 2343–2347. [Google Scholar]
- Fan, R.; Mu, F.; Su, M. DFT-based pilot-symbol-aided channel estimation in OFDM systems. J. Nanjing Univers. Posts Telecommun. 2015, 2, 79–83. [Google Scholar]
- Fan, T.; Yang, S.; Wu, H.; Wang, D. Two Novel Channel Estimation for OFDM Systems by Time-Domain Cluster Discriminant Analysis Based on Parametric Channel Modeling. Wirel. Pers. Commun. 2013, 2, 349–360. [Google Scholar] [CrossRef]
- Ma, X.; Fan, T.; Du, Y. An Improved DFT-Based Channel Estimation Algorithm for OFDM System on Time-Varying Multipath Fading Channels. Adv. Mater. Res. 2014, 989–994, 3786–3789. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, H.; Liu, X.; Yang, L.T.; Leung, V.C.M. A Novel Sensory Data Processing Framework to Integrate Sensor Networks With Mobile Cloud. IEEE Syst. J. 2016, 3, 1125–1136. [Google Scholar] [CrossRef]
- Du, Q.; Song, H.; Xu, Q.; Ren, P.; Sun, L. Interference-controlled D2D routing aided by knowledge extraction at cellular infrastructure towards ubiquitous CPS. Pers. Ubiquitous Comput. 2015, 7, 1033–1043. [Google Scholar] [CrossRef]
- Zhu, J.; Song, Y.; Jiang, D.; Song, H. A New Deep-Q-Learning-Based Transmission Scheduling Mechanism for the Cognitive Internet of Things. IEEE Internet Things J. 2018, 4, 2375–2385. [Google Scholar] [CrossRef]
- Liu, F.; Zhao, H.; Quan, X.; Liu, Y.; Tang, Y. Eigen Domain Interference Rejection Combining Algorithm for MIMO Systems. IEEE Commun. Lett. 2016, 5, 850–853. [Google Scholar] [CrossRef]
- Deng, X.; Tang, Z.; Yang, L.T.; Lin, M.; Wang, B. Confident Information Coverage Hole Healing in Hybrid Industrial Wireless Sensor Networks. IEEE Trans. Ind. Inform. 2018, 5, 2220–2229. [Google Scholar] [CrossRef]
- Hadaschik, N.; Zakia, I.; Ascheid, G.; Meyr, H. Joint Narrowband Interference Detection and Channel Estimation for Wideband OFDM. In Proceedings of the European Wireless Conference 2007, Paris, France, 1–4 April 2007. [Google Scholar]
- Islam, S.M.R.; Iqbal, A.; Kwak, K.S. Joint Channel Estimation and Interference Suppressions for MB-OFDM UWB Systems. In Proceedings of the 2010 6th International Conference on Wireless Communications Networking and Mobile Computing (WiCOM), Chengdu, China, 23–25 September 2010. [Google Scholar]
- Zhang, L.; Ijaz, A.; Xiao, P.; Tafazolli, R. Channel Equalization and Interference Analysis for Uplink Narrowband Internet of Things (NB-IoT). IEEE Commun. Lett. 2017, 10, 2206–2209. [Google Scholar] [CrossRef]
- Yi, L.; Deng, X.; Wang, M.; Ding, D.; Wang, Y. Localized Confident Information Coverage Hole Detection in Internet of Things for Radioactive Pollution Monitoring. IEEE Access 2017, 5, 18665–18674. [Google Scholar] [CrossRef]
- Al-Tous, H.; Barhumi, I.; Al-Dhahir, N. Narrow-Band Interference Mitigation Using Compressive Sensing for AF-OFDM Systems. IEEE Trans. Veh. Technol. 2017, 9, 2741–2748. [Google Scholar] [CrossRef]
- Deng, X.; Tang, Z.; Yi, L.; Yang, L.T. Healing Multi-modal Confident Information Coverage Holes in NB-IoT-Enabled Networks. IEEE Internet Things J. 2018, 3, 1463–1473. [Google Scholar] [CrossRef]
- Likas, A.; Vlassis, N.; Verbeek, J.J. The global k-means clustering algorithm. Pattern Recogn. 2003, 2, 451–461. [Google Scholar] [CrossRef]
- Arora, P.; Deepali, D.; Varshney, S. Analysis of K-Means and K-Medoids Algorithm For Big Data. Procedia Comput. Sci. 2016, 78, 507–512. [Google Scholar] [CrossRef]
- Keller, J.M.; Gray, M.R.; Givens, J.A. A fuzzy K-nearest neighbor algorithm. IEEE Trans. Syst. Man Cybern. 2012, 4, 580–585. [Google Scholar] [CrossRef]
- Chaudhuri, K.; Dasgupta, S. Rates of Convergence for Nearest Neighbor Classification. Adv. Neural Inf. Process. Syst. 2014, 4, 3437–3445. [Google Scholar]
- Dorazio, C.J.; Choo, K.K.R.; Yang, L.T. Data Exfiltration from Internet of Things Devices: iOS Devices as Case Studies. IEEE Internet Things J. 2017, 2, 524–535. [Google Scholar] [CrossRef]
- Dhar, S.K.; Bhunia, S.S.; Mukherjee, N. Interference Aware Scheduling of Sensors in IoT Enabled Health-Care Monitoring System. In Proceedings of the 2014 Fourth International Conference of Emerging Applications of Information Technology, Kolkata, India, 19–21 December 2014; pp. 152–157. [Google Scholar]
- Zhang, Z.; Wang, H.; Wang, C.; Fang, H. Interference Mitigation for Cyber-Physical Wireless Body Area Network System Using Social Networks. IEEE Trans. Emerg. Top. Comput. 2013, 1, 121–132. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Yang, L.; Shen, X. D2D for Intelligent Transportation Systems: A Feasibility Study. IEEE Trans. Intell. Transp. Syst. 2015, 4, 1784–1793. [Google Scholar] [CrossRef]







| Algorithm Modules | Basis of Algorithm | Core Operator | Computation |
|---|---|---|---|
| FFT transformation | Radix-4 | 16b × 16b MAC | 1013.76 M |
| LS estimation | Least square | 16b × 16b MA | 122.88 M |
| Interference detection | K-means | 16b × 16b MAC | 122.88 M |
| Interference suppression | Linear interpolation | 16b × 16b MA | negligible |
| noise cancellation 1 | KNN | 16b × 16b MAC | 368.64 M |
| noise cancellation 2 | Windowing | 16b × 16b MAC | 245.76 M |
| noise cancellation 3 | Mahalanobis distance | 16b × 16b MA | 368.64 M |
| Parameters | Specifications |
|---|---|
| Carrier frequency | 400 MHz–700 MHz |
| Modulation type | 16 QAM |
| Transmission rate | 23.56 Mbps |
| Subcarrier number | 1024 |
| Subcarrier spacing | 15 kHz |
| Channel codes | Turbo |
| Tap Number | Average Power (dB) | Relative Delay (ns) |
|---|---|---|
| 0 | −3 | 0 |
| 1 | 0 | 200 |
| 2 | −2 | 600 |
| 3 | −6 | 1600 |
| 4 | −8 | 2400 |
| 5 | −10 | 5000 |
| Simulation Scene | Interference Style | JSR | Interference Suppression Method |
|---|---|---|---|
| Scene 1 | No interference | – | – |
| Scene 2 | Single tone | JSR = 10 dB | With nothing done |
| Scene 3 | Single tone | JSR = 10 dB | Zero force |
| Scene 4 | Single tone | JSR = 10 dB | Linear interpolation |
| Scene 5 | multitone with 10 subcarriers | JSR = 10 dB | Linear interpolation |
| Scene 6 | multitone with 10 subcarriers | JSR = 15 dB | Linear interpolation |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, X.; Wang, H. Combined Channel Estimation with Interference Suppression in CPSS. Sensors 2018, 18, 3823. https://doi.org/10.3390/s18113823
Lai X, Wang H. Combined Channel Estimation with Interference Suppression in CPSS. Sensors. 2018; 18(11):3823. https://doi.org/10.3390/s18113823
Chicago/Turabian StyleLai, Xiaoyang, and Huan Wang. 2018. "Combined Channel Estimation with Interference Suppression in CPSS" Sensors 18, no. 11: 3823. https://doi.org/10.3390/s18113823
APA StyleLai, X., & Wang, H. (2018). Combined Channel Estimation with Interference Suppression in CPSS. Sensors, 18(11), 3823. https://doi.org/10.3390/s18113823




