A Low-Cost Resource Re-Allocation Scheme for Increasing the Number of Guaranteed Services in Resource-Limited Vehicular Networks
Abstract
:1. Introduction
1.1. Motivation
1.2. Related Work
1.3. Contributions
- The co-layer and cross-layer interferences in the vehicular network are quantitatively analyzed using stochastic geometry.
- To guarantee the services in the dynamic network, the definition of the guaranteed service is given based on the changes in the data queue.
- To increase the number of guaranteed services at a low cost in a resource-limited vehicular network, we propose a time dynamic optimization method that constrains the network re-allocation rate.
- To decrease the computational complexity, we convert the proposed time dynamic optimization problem into a deterministic optimization problem using the Lyapunov optimization theory to determine the set of served services based on the dynamic changes in the network at each slot.
1.4. Organization
2. System Model and Dynamic Optimization Problem
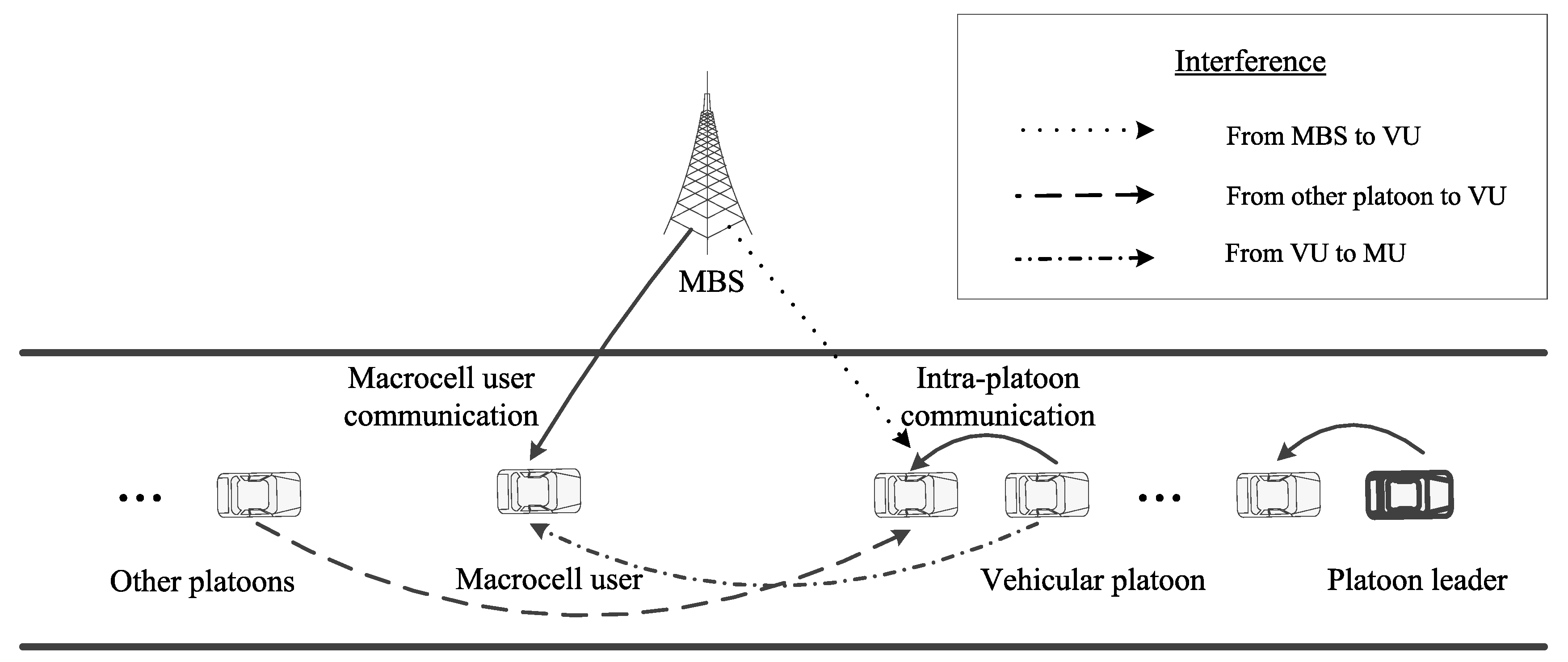
2.1. Network Model
2.2. Signal Model
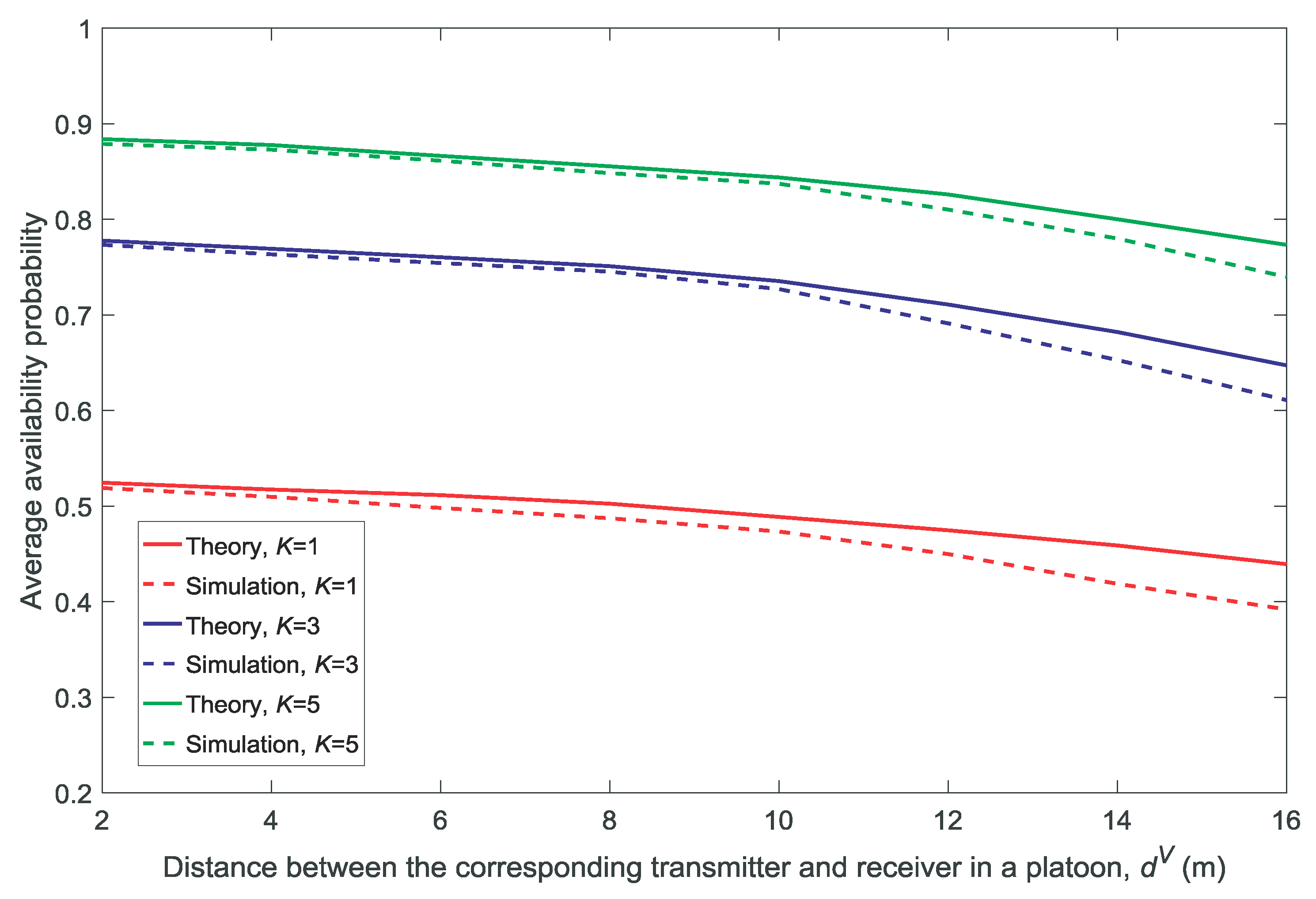
2.3. Availability Probability Calculated by Stochastic Geometry
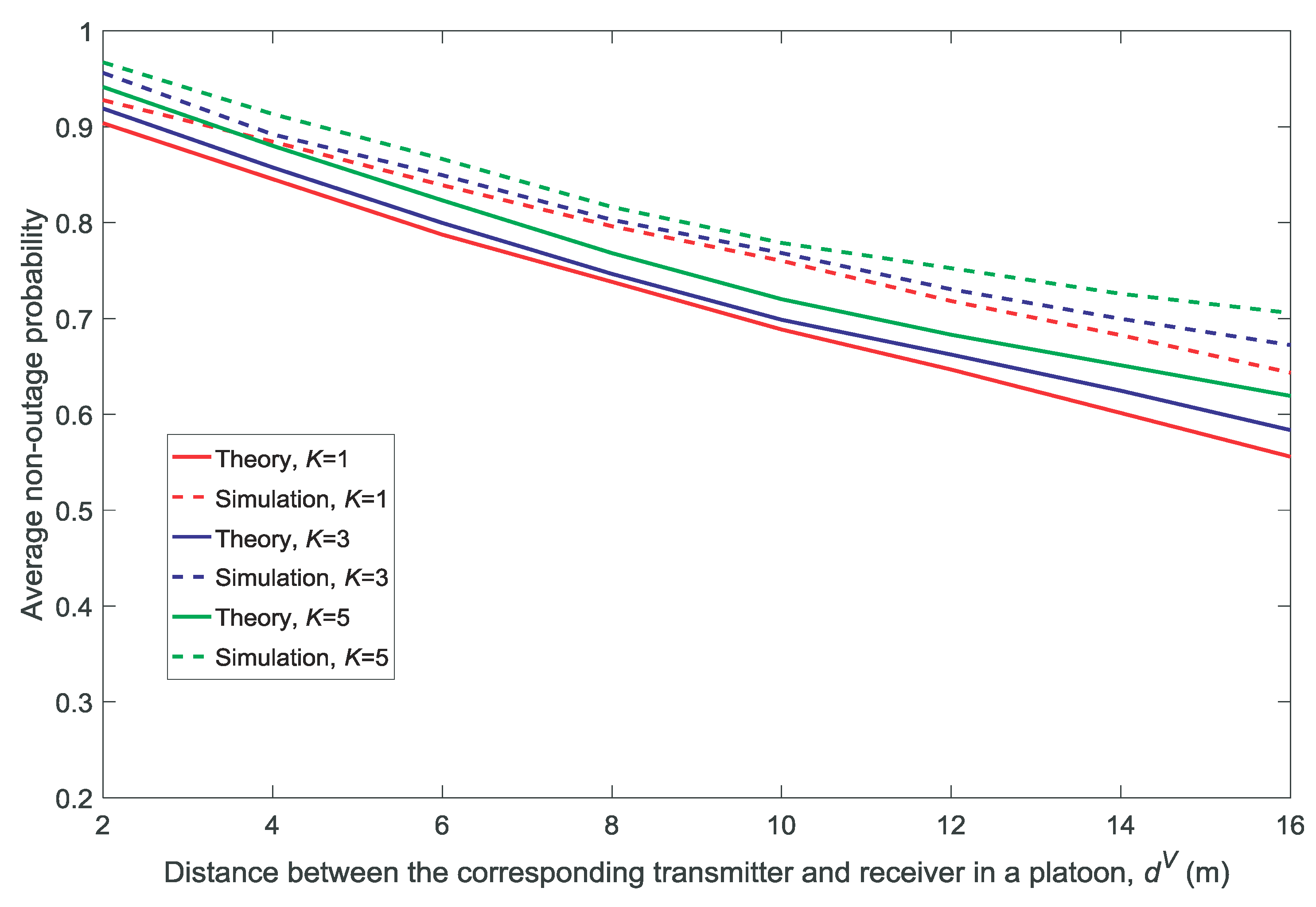
2.4. Non-Outage Probability Calculated by Stochastic Geometry
2.5. Data Queue Model
2.6. Dynamic Maximization Problem of the Number of Service-Guaranteed Users
3. Dynamic Algorithm of Resource Re-allocation
3.1. Virtual Queue
3.2. Lyapunov Optimization
3.3. Implementation of the Proposed Resource Allocation Scheme and Its Overhead
4. Simulation
4.1. Comparison between the Theoretical Calculations and the Simulation Results
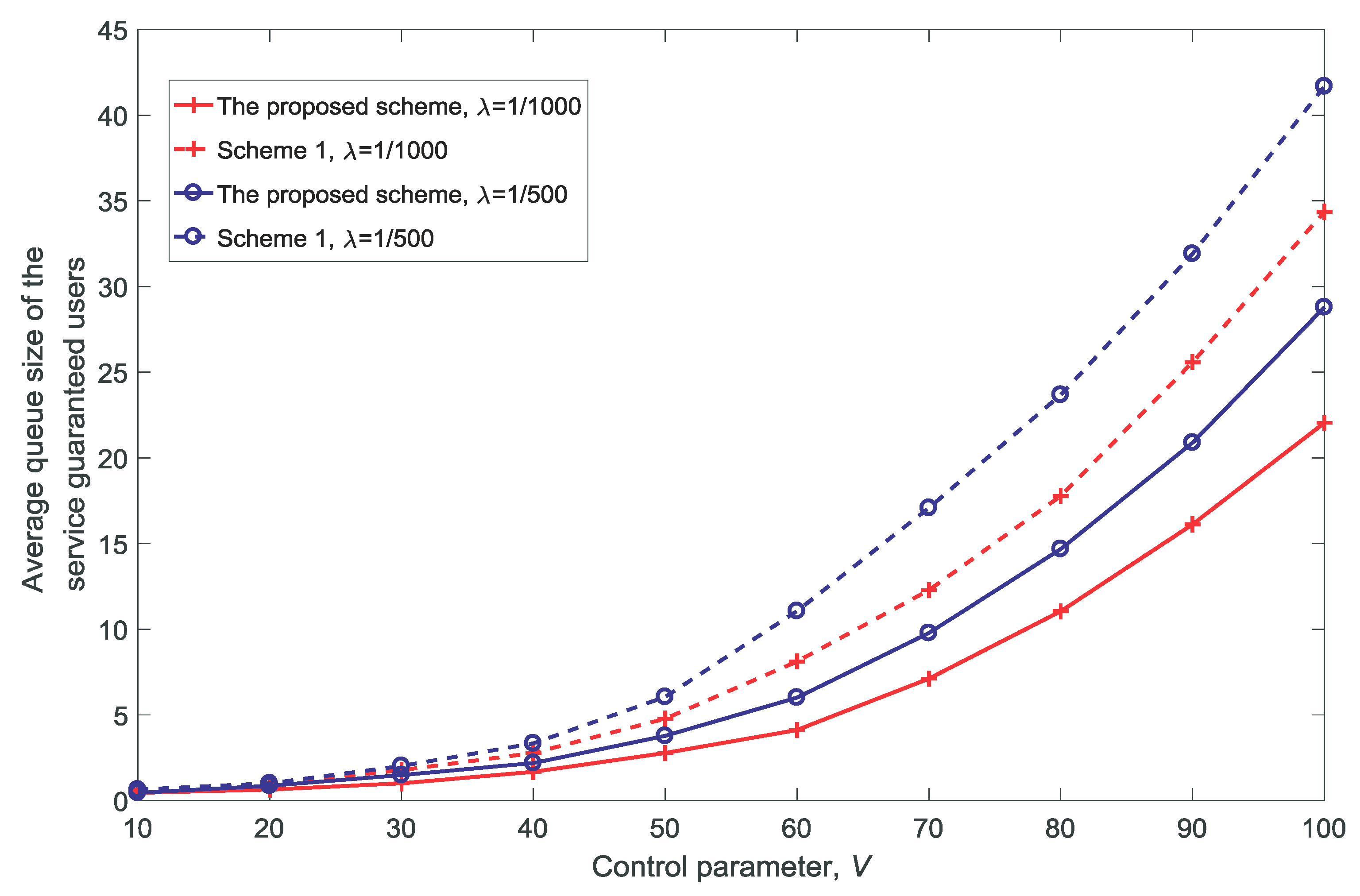
4.2. The Performance of the Proposed Scheme
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ITS | intelligent transportation system |
| V2V | vehicle-to-vehicle |
| V2I | vehicle-to-infrastructure |
| C-V2X | cellular vehicle-to-everything |
| RSU | roadside unit |
| VU | vehicular user |
| MU | macrocell user |
| MBS | macrocell base station |
| 1D PPP | one-dimensional Poisson point process |
| SIR | signal-to-interference-ratio |
References
- Wang, J.; Qi, Q.; Qing, S.; Liao, J. Elastic Vehicular Resource Providing Based on Service Function-Group Resource Mapping of Smart Identify Network. IEEE Syst. J. 2018, 67, 1897–1908. [Google Scholar] [CrossRef]
- Gu, Y.; Cai, L.X.; Pan, M.; Song, L.; Han, Z. Exploiting the Stable Fixture Matching Game for Content Sharing in D2D-Based LTE-V2X Communications. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Chen, S.; Hu, J.; Shi, Y.; Peng, Y.; Fang, J.; Zhao, R.; Zhao, L. Vehicle-to-Everything (v2x) Services Supported by LTE-Based Systems and 5G. IEEE Commun. Standard. Mag. 2017, 1, 70–76. [Google Scholar] [CrossRef]
- Cheng, H.T.; Shan, H.; Zhuang, W. Infotainment and road safety service support in vehicular networking: From a communication perspective. Mech. Syst. Sig. Process. 2011, 25, 2020–2038. [Google Scholar] [CrossRef]
- Wang, M.; Shan, H.; Lu, R.; Zhang, R. Real-Time Path Planning Based on Hybrid-VANET-Enhanced Transportation System. IEEE Trans. Veh. Technol. 2015, 64, 1664–1678. [Google Scholar] [CrossRef]
- Masini, B.M.; Bazzi, A.; Natalizio, E. Radio Access for Future 5G Vehicular Networks. In Proceedings of the IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, ON, Canada, 24–27 September 2017; pp. 1–7. [Google Scholar]
- Zelikman, D.; Segal, M. Reducing Interferences in VANETs. IEEE Trans. Intell. Transp. Syst. 2015, 16, 1582–1587. [Google Scholar] [CrossRef]
- Cheng, N.; Zhou, H.; Lei, L.; Zhang, N.; Zhou, Y.; Shen, X.; Bai, F. Performance Analysis of Vehicular Device-to-Device Underlay Communication. IEEE Trans. Veh. Technol. 2017, 66, 5409–5421. [Google Scholar] [CrossRef]
- Hsieh, H.Y.; Juan, T.C.; Tsai, Y.D.; Huang, H.C. Minimizing Radio Resource Usage for Machine-to-Machine Communications through Data-Centric Clustering. IEEE Trans. Mob. Comput. 2016, 15, 3072–3086. [Google Scholar] [CrossRef]
- Li, G.; Yang, Z.; Chen, S.; Li, Y.; Yuan, P. A traffic flow-based and dynamic grouping-enabled resource allocation algorithm for LTE-D2D vehicular networks. In Proceedings of the IEEE/CIC International Conference on Communications in China (ICCC), Chengdu, China, 27–29 July 2016; pp. 1–6. [Google Scholar]
- Liang, L.; Li, G.Y.; Xu, W. Meeting different QoS requirements of vehicular networks: A D2D-based approach. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 3734–3738. [Google Scholar]
- Le, L.; Geoffrey, L.Y.; Xu, W. Resource Allocation for D2D-Enabled Vehicular Communications. IEEE Trans. Commun. 2017, 65, 3186–3197. [Google Scholar]
- Jangsher, S.; Li, V.O.K. Resource Allocation in Moving Small Cell Network. IEEE Trans. Wireless Commun. 2016, 15, 4559–4570. [Google Scholar] [CrossRef]
- Zheng, Q.; Zheng, K.; Zhang, H.; Leung, V.C.M. Delay-Optimal Virtualized Radio Resource Scheduling in Software-Defined Vehicular Networks via Stochastic Learning. IEEE Trans. Veh. Technol. 2016, 65, 7857–7867. [Google Scholar] [CrossRef]
- Cao, X.; Liu, L.; Cheng, Y.; Cai, L.X.; Sun, C. On Optimal Device-to-Device Resource Allocation for Minimizing End-to-End Delay in VANETs. IEEE Trans. Veh. Technol. 2016, 65, 7905–7916. [Google Scholar] [CrossRef]
- Sun, L.; Shan, H.; Huang, A.; Cai, L.; He, H. Channel Allocation for Adaptive Video Streaming in Vehicular Networks. IEEE Trans. Veh. Technol. 2017, 66, 734–747. [Google Scholar] [CrossRef]
- Tao, J.; Zhang, Z.; Feng, F.; He, J.; Xu, Y. Non-cooperative Resource Allocation Scheme for Data Access in VANET Cloud Environment. In Proceedings of the Third International Conference on Advanced Cloud and Big Data, Yangzhou, China, 30 October–1 November 2015; pp. 1–7. [Google Scholar]
- Qi, Y.; Wang, H.; Zhang, L.; Wang, B. Optimal access mode selection and resource allocation for cellular-VANET heterogeneous networks. IET Commun. 2017, 11, 2012–2019. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, R.; Chen, C.; Cheng, X. Secrecy-Based Resource Allocation for Vehicular Communication Networks with Outdated CSI. In Proceedings of the IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, ON, Canada, 24–27 September 2017; pp. 1–5. [Google Scholar]
- Hou, X.; Li, Y.; Jin, D.; Wu, D.O.; Chen, S. Modeling the impact of mobility on the connectivity of vehicular networks in large-scale urban environments. IEEE Trans. Veh. Technol. 2016, 65, 2753–2758. [Google Scholar] [CrossRef]
- Niu, C.; Li, Y.; Hu, R.Q.; Ye, F. Fast and Efficient Radio Resource Allocation in Dynamic Ultra-Dense Heterogeneous Networks. IEEE Access 2017, 5, 1911–1924. [Google Scholar] [CrossRef]
- Hung, S.C.; Zhang, X.; Festag, A.; Chen, K.C.; Fettweis, G. An Efficient Radio Resource Re-Allocation Scheme for Delay Guaranteed Vehicle-to-Vehicle Network. In Proceedings of the IEEE 84th Vehicular Technology Conference (VTC-Fall), Montreal, QC, Canada, 18–21 September 2016; pp. 1–6. [Google Scholar]
- Hung, S.C.; Zhang, X.; Festag, A.; Chen, K.C.; Fettweis, G. Virtual Cells and Virtual Networks Enable Low-Latency Vehicle-to-Vehicle Communication. In Proceedings of the GLOBECOM 2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–7. [Google Scholar]
- Vukadinovic, V.; Bakowski, K.; Marsch, P.; Garcia, I.D.; Xu, H.; Sybis, M.; Sroka, P.; Wesolowski, K.; Lister, D.; Thibault, I. 3GPP C-V2X and IEEE 802.11 p for Vehicle-to-Vehicle communications in highway platooning scenarios. Ad Hoc Netw. 2018, 74, 17–29. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.E.; Li, K.; Wang, L.Y. Stability and Scalability of Homogeneous Vehicular Platoon: Study on the Influence of Information Flow Topologies. IEEE Trans. Intell. Transp. Syst. 2016, 17, 14–26. [Google Scholar] [CrossRef]
- Ucar, S.; Ergen, S.C.; Ozkasap, O. IEEE 802.11p and Visible Light Hybrid Communication based Secure Autonomous Platoon. IEEE Trans. Veh. Technol. 2018, 67. [Google Scholar] [CrossRef]
- Peng, H.; Li, D.; Ye, Q.; Abboud, K.; Zhao, H.; Zhuang, W.; Shen, X.S. Resource allocation for D2D-enabled inter-vehicle communications in multiplatoons. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Tong, Z.; Lu, H.; Haenggi, M.; Poellabauer, C. A Stochastic Geometry Approach to the Modeling of DSRC for Vehicular Safety Communication. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1448–1458. [Google Scholar] [CrossRef]
- Martın-Vega, F.J.; Soret, B.; Aguayo-Torres, M.C.; Kovacs, I.Z.; Gomez, G. Geolocation-Based Access for Vehicular Communications: Analysis and Optimization via Stochastic Geometry. IEEE Trans. Veh. Technol. 2018, 67, 3069–3084. [Google Scholar] [CrossRef] [Green Version]
- Blaszczyszyn, B.; Mühlethaler, P.; Toor, Y. Maximizing throughput of linear vehicular Ad-hoc NETworks (VANETs)—A stochastic approach. In Proceedings of the European Wireless Conference, Aalborg, Denmark, 17–20 May 2009; pp. 32–36. [Google Scholar]
- Study on LTE-Based V2X services (Release 14). Technical Report Document 3GPP TR 36.885, Technical Specication Group Radio Access. 2016. Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=2934 (accessed on 17 August 2018).
- Georgiadis, L.; Neely, M.J.; Tassiulas, L. Resource Allocation And Cross-Layer Control In Wireless Networks. Found. Trends Netw. 2006, 1, 1–144. [Google Scholar] [CrossRef]
- Stoyan, D.; Kendall, W.S.; Mecke, J. Stochastic Geometry and its Applications. J. Royal Stat. Soc. 2013, 45, 345. [Google Scholar] [CrossRef]













| Notations | Meaning |
|---|---|
| The set of platoons | |
| The density of platoons | |
| The set of vehicles in a platoon | |
| N | The cardinality of |
| The set of orthogonal channels | |
| and | The number of microcell users (MUs) and the number of platoons |
| The threshold of the signal-to-interference ratio (SIR) | |
| and | The transmit power of the microcell base station (MBS) and the transmit power of the vehicle user (VU) |
| The factor of the path loss | |
| n | The member in the platoon |
| The interference from the MBS to member n in the platoon in channel k | |
| The small-scale fading from the MBS to member n in the platoon in channel k | |
| The distance between the MBS and the platoon | |
| The probability of a channel being occupied by an MU | |
| The aggregated interference from the other platoons to member n in the platoon in channel k | |
| The small-scale fading from the VU interferer q to member n in the platoon in channel k | |
| The distance between the VU interferer q and the platoon | |
| The total aggregated interference from the MBS and the other platoons to member n in the platoon in channel k | |
| The SIR of member n in the platoon in channel k | |
| The small-scale fading from the corresponding transmitter to member n in the platoon in channel k | |
| The distance between the corresponding transmitter and receiver in the platoon | |
| The small-scale fading from the MBS to the corresponding MU that is active in channel k | |
| The distance between the MBS and the corresponding MU that is active in channel k | |
| The small-scale fading from the VU interferer to the MU that is active in channel k | |
| The distance between the VU interferer and the MU that is active in channel k | |
| The threshold of the ratio of the interference from the MBS to the interference from the other platoons | |
| The binary variable of channel allocation for the MUs in channel k | |
| The availability probability of channel k for member n in the platoon | |
| The binary variable that indicates whether channel k is available to member n in the platoon at time slot t | |
| The non-outage probability of channel k for member n in the platoon | |
| The binary variable that indicates whether channel k is in a non-outage state for member n in the platoon at time slot t | |
| The data queue for member n in the platoon at time slot t | |
| The rate of service for member n in the platoon at time slot t | |
| The rate of data arrival for member n in the platoon | |
| and | The channel allocation matrix and its element |
| The set of decisions for member n in the platoon | |
| The indicator of re-allocation at time slot t | |
| The threshold of re-allocation rate | |
| The notation that indicates whether member n in the platoon is a service-guaranteed user at time slot t | |
| The virtual cost queue for the re-allocation rate of the platoon at time slot t | |
| and | The Lyapunov function and the Lyapunov drift at time slot t |
| V | The control parameter |
| Simulation Parameters | Value |
|---|---|
| The threshold of the SIR, | 5 |
| The path loss factor, | 4 |
| The transmit power of the MBS, | 10 w |
| The transmit power of the VU, | 3 w |
| The threshold of the re-allocation rate, | 0.2 |
| The length of each slot, | 10 ms |
| The velocity of the platoon and MU | 40 km/h |
| The length of the road | 2000 m |
| The maximum data arrival rate of the VUs, | 1 packet/slot |
| The minimum data arrival rate of the VUs, | 0.1 packet/slot |
| The number of MUs, | 2 |
| The threshold of the ratio of the interference from the MBS to the interference from the other platoons, | 1 |
| The window of the service-guaranteed user, W | 10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, Y.; Dong, Y.; Wu, C.; Liu, X. A Low-Cost Resource Re-Allocation Scheme for Increasing the Number of Guaranteed Services in Resource-Limited Vehicular Networks. Sensors 2018, 18, 3846. https://doi.org/10.3390/s18113846
Meng Y, Dong Y, Wu C, Liu X. A Low-Cost Resource Re-Allocation Scheme for Increasing the Number of Guaranteed Services in Resource-Limited Vehicular Networks. Sensors. 2018; 18(11):3846. https://doi.org/10.3390/s18113846
Chicago/Turabian StyleMeng, Yun, Yuan Dong, Chunling Wu, and Xinyi Liu. 2018. "A Low-Cost Resource Re-Allocation Scheme for Increasing the Number of Guaranteed Services in Resource-Limited Vehicular Networks" Sensors 18, no. 11: 3846. https://doi.org/10.3390/s18113846





