Outage-Based Resource Allocation for DF Two-Way Relay Networks with Energy Harvesting
Abstract
:1. Introduction
2. System Model and Problem Formulation
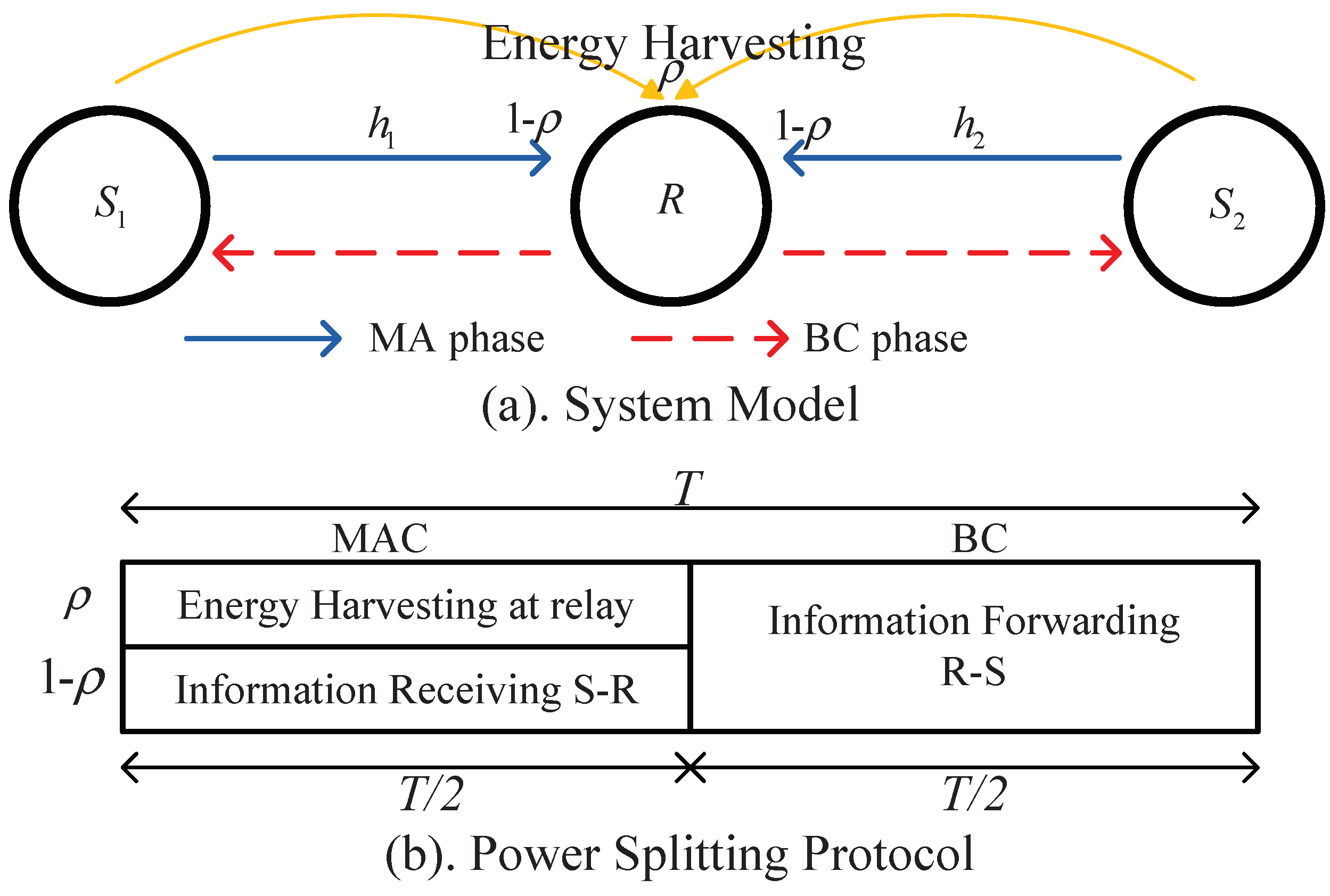
2.1. System Model
2.2. Performance Metric
2.3. Problem Formulation
3. A Two-Step Optimization Algorithm
3.1. Case 1:
3.1.1. Subcase 1:
3.1.2. Subcase 2:
3.1.3. Subcase 3:
3.2. Case 2:
3.2.1. Subcase 1:
3.2.2. Subcase 2:
3.2.3. Subcase 3:
4. The Closed-Form of PA and PS
| Algorithm 1 Optimal joint resource allocation for , . |
|
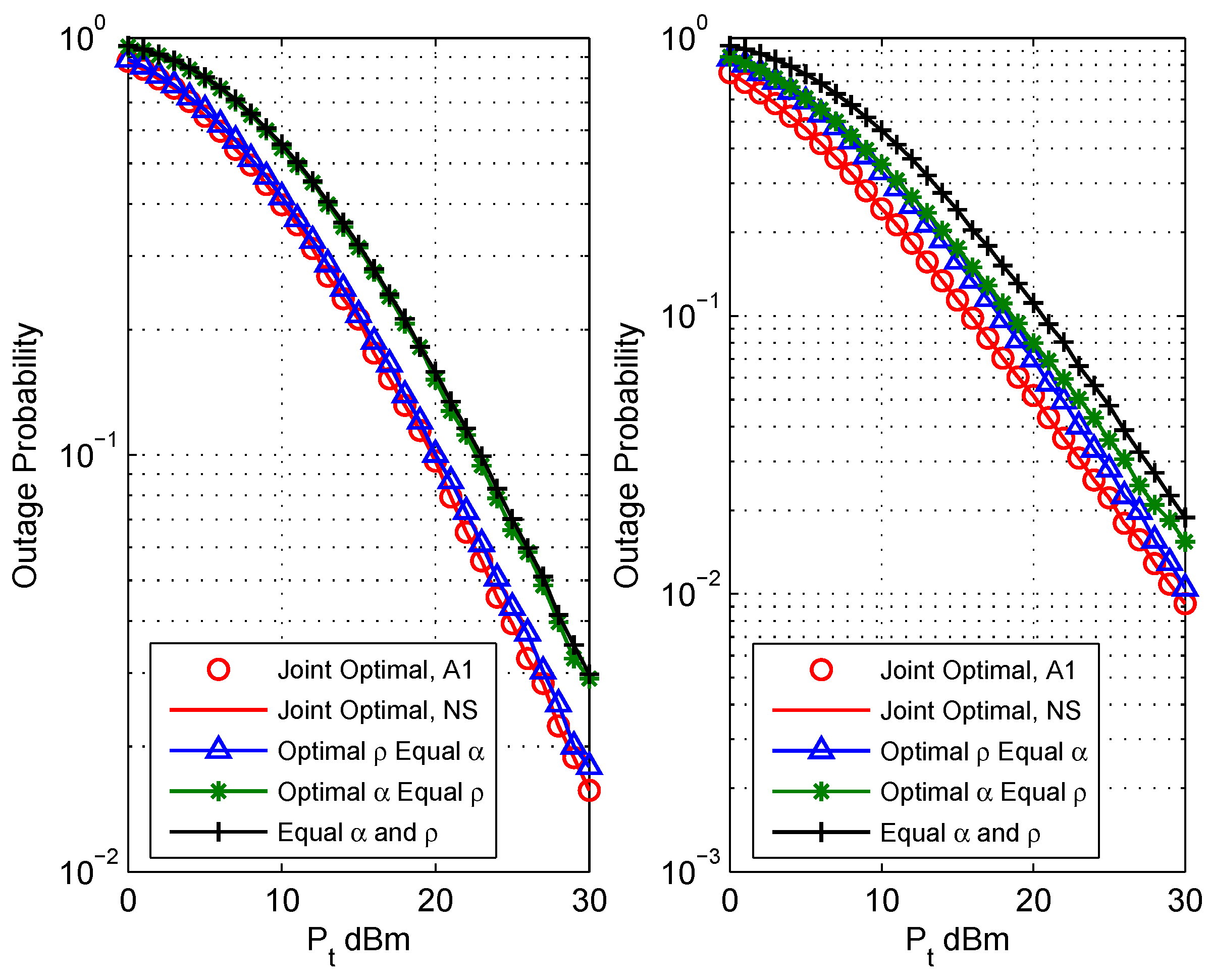
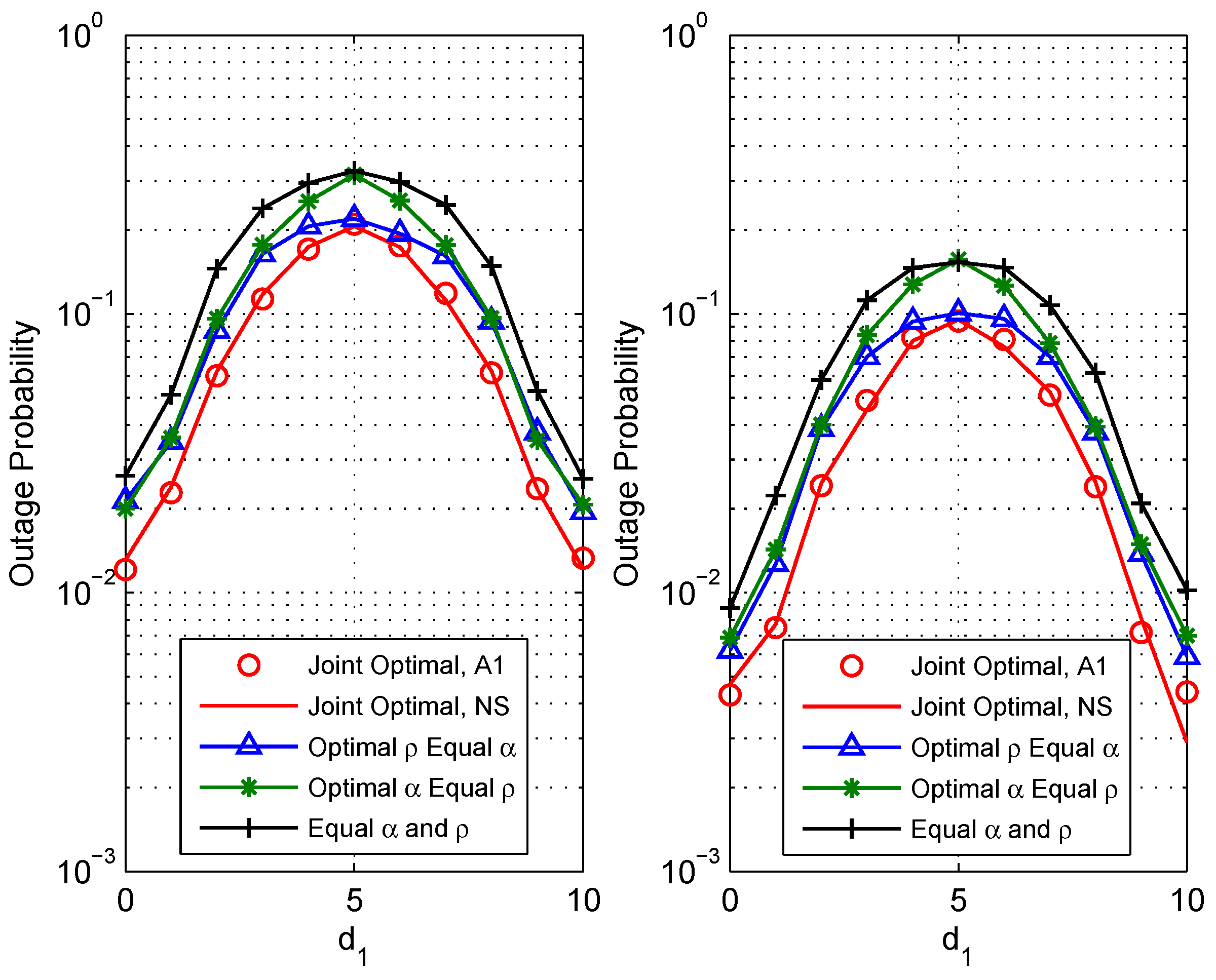
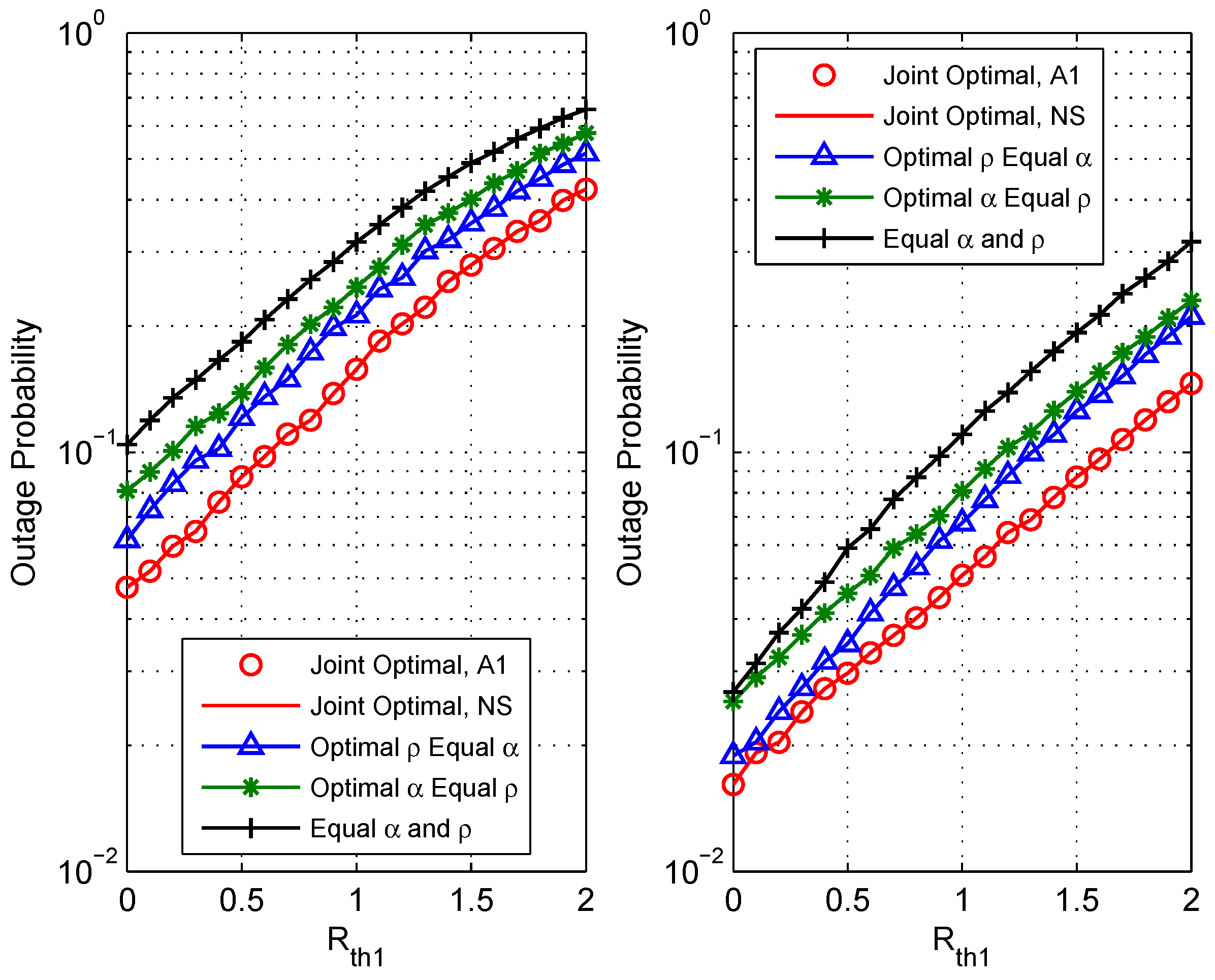
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DF | Decode-and-forward |
| SWIPT | Simultaneous wireless information and power transfer |
| PS | Power splitting |
| PA | Power allocation |
| CSI | Channel state information |
| TWR | Two-way relay |
| AF | Amplify-and-forward |
| EH | Energy harvesting |
| MA | Multiple access |
| BC | Broadcast |
| ID | Information decoding |
| SNR | Signal-to-noise ratio |
| CDF | Cumulative distribution function |
| CSI | Channel state information |
Appendix A
References
- Liu, K.J.R.; Sadek, A.K.; Su, W.; Kwasinski, A. Cooperative Communications and Networking; Cambridge University Press: Cambridge, UK, 2009; ISBN 9780521895132. [Google Scholar]
- Hong, Y.W.P.; Huang, W.J.; Kuo, C.C.J. Cooperative Communications and Networking: Technologies and System Design; Springer: Berlin, Germany, 2010; ISBN 1489998578. [Google Scholar]
- Zhang, S.; Liew, S.; Lam, P. Hot Topic: Physical-Layer Network Coding. In Proceedings of the 12th Annual International Conference on Mobile Computing and Networking, Los Angeles, CA, USA, 23–29 September 2006; pp. 358–365. [Google Scholar] [CrossRef]
- Kim, S.J.; Mitran, P.; Tarokh, V. Performance bounds for bidirectional coded cooperation protocols. IEEE Trans. Inf. Theory 2008, 54, 5235–5241. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.; Kim, I.M. Performance analysis of bidirectional communication protocols based on decode-and-forward relaying. IEEE Trans. Commun. 2010, 58, 2683–2696. [Google Scholar] [CrossRef]
- Rodríguez, L.J.; Tran, N.; Le-Ngoc, T. Achievable rates and power allocation for two-way AF relaying over Rayleigh fading channels. In Proceedings of the 2013 IEEE International Conference on Communications (ICC), Budapest, Hungary, 9–13 June 2013; pp. 5914–5918. [Google Scholar] [CrossRef]
- Pang, L.; Zhang, Y.; Li, J.; Ma, Y.; Wang, J. Power allocation and relay selection for two-way relaying systems by exploiting physical-layer network coding. IEEE Trans. Veh. Technol. 2014, 63, 2723–2730. [Google Scholar] [CrossRef]
- Do, T.P.; Kim, Y.H. Outage-optimal power and time allocation for rate-aware two-way relaying with a decode-and-forward protocol. IEEE Trans. Veh. Technol. 2016, 65, 9673–9686. [Google Scholar] [CrossRef]
- Chen, Z.; Xia, B.; Liu, H. Wireless information and power transfer in two-way amplify-and-forward relaying channels. In Proceedings of the 2014 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Atlanta, GA, USA, 3–5 December 2014; pp. 168–172. [Google Scholar] [CrossRef]
- Men, J.; Ge, J.; Zhang, C.; Li, J. Joint optimal power allocation and relay selection scheme in energy harvesting asymmetric two-way relaying system. IET Commun. 2015, 9, 1421–1426. [Google Scholar] [CrossRef]
- Fang, Z.; Yuan, X.; Wang, X. Distributed energy beamforming for simultaneous wireless information and power transfer in the two-way relay channel. IEEE Signal Process. Lett. 2015, 22, 656–660. [Google Scholar] [CrossRef]
- Nguyen, T.P.V.; Syed, F.H.; Xiang, G.; Subhas, M.; Hung, T. Three-Step Two-Way Decode and Forward Relay With Energy Harvesting. IEEE Commun. Lett. 2017, 21, 857–860. [Google Scholar] [CrossRef]
- Do, T.P.; Song, I.; Kim, Y.H. Simultaneous Wireless Transfer of Power and Information in a Decode-and-Forward Two-Way Relaying Network. IEEE Trans. Wirel. Commun. 2017, 16, 1579–1592. [Google Scholar] [CrossRef]
- Kim, S.; Devroye, N.; Mitra, P.; Tarokh, V. Achievable rate regions and performance comparison of half duplex bi-directional relaying protocols. IEEE Trans. Inf. Theory 2011, 57, 6405–6418. [Google Scholar] [CrossRef]
- Ciccone, V.; Ferrante, A.; Zorzi, M. An alternating minimization algorithm for Factor Analysis. arXiv, 2018; arXiv:1806.04433. [Google Scholar]
- Mishra, D.; De, S.; Chiasserini, C. Joint Optimization Schemes for Cooperative Wireless Information and Power Transfer Over Rician Channels. IEEE Trans. Commun. 2016, 64, 554–571. [Google Scholar] [CrossRef] [Green Version]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, C.; Li, F.; Liu, H.; Wang, G. Outage-Based Resource Allocation for DF Two-Way Relay Networks with Energy Harvesting. Sensors 2018, 18, 3946. https://doi.org/10.3390/s18113946
Peng C, Li F, Liu H, Wang G. Outage-Based Resource Allocation for DF Two-Way Relay Networks with Energy Harvesting. Sensors. 2018; 18(11):3946. https://doi.org/10.3390/s18113946
Chicago/Turabian StylePeng, Chunling, Fangwei Li, Huaping Liu, and Guozhong Wang. 2018. "Outage-Based Resource Allocation for DF Two-Way Relay Networks with Energy Harvesting" Sensors 18, no. 11: 3946. https://doi.org/10.3390/s18113946



