Investigation on the Influence of Humidity on Stimulated Brillouin Backscattering in Perfluorinated Polymer Optical Fibers
Abstract
:1. Introduction
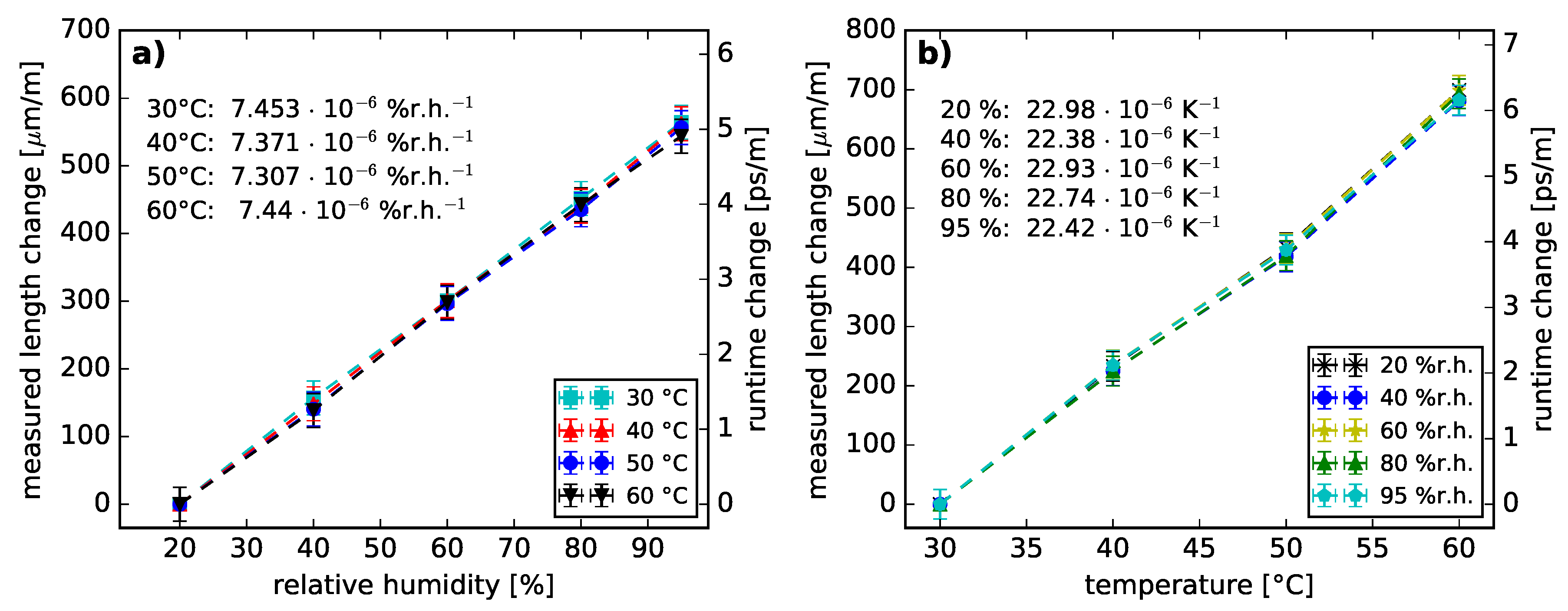
2. Fiber Characterization
2.1. Spectral Absorption
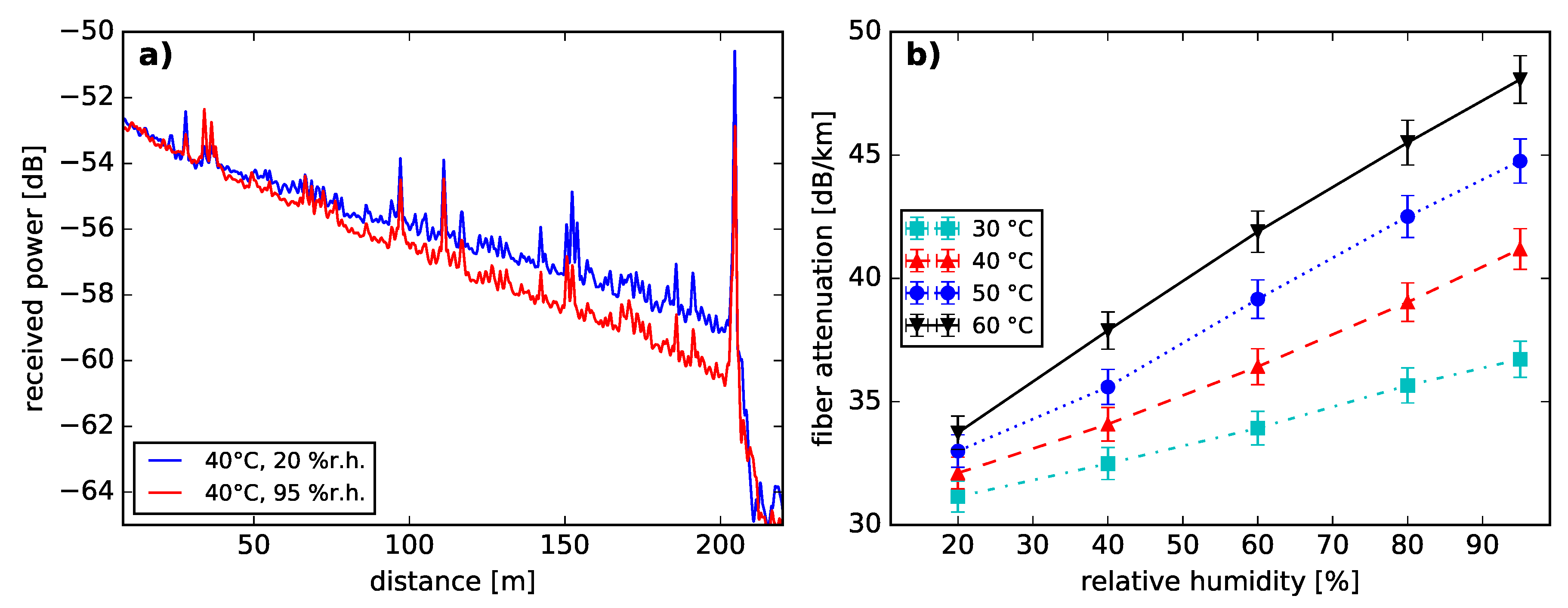
2.2. Rayleigh Backscattering
3. Stimulated Brillouin Backscattering
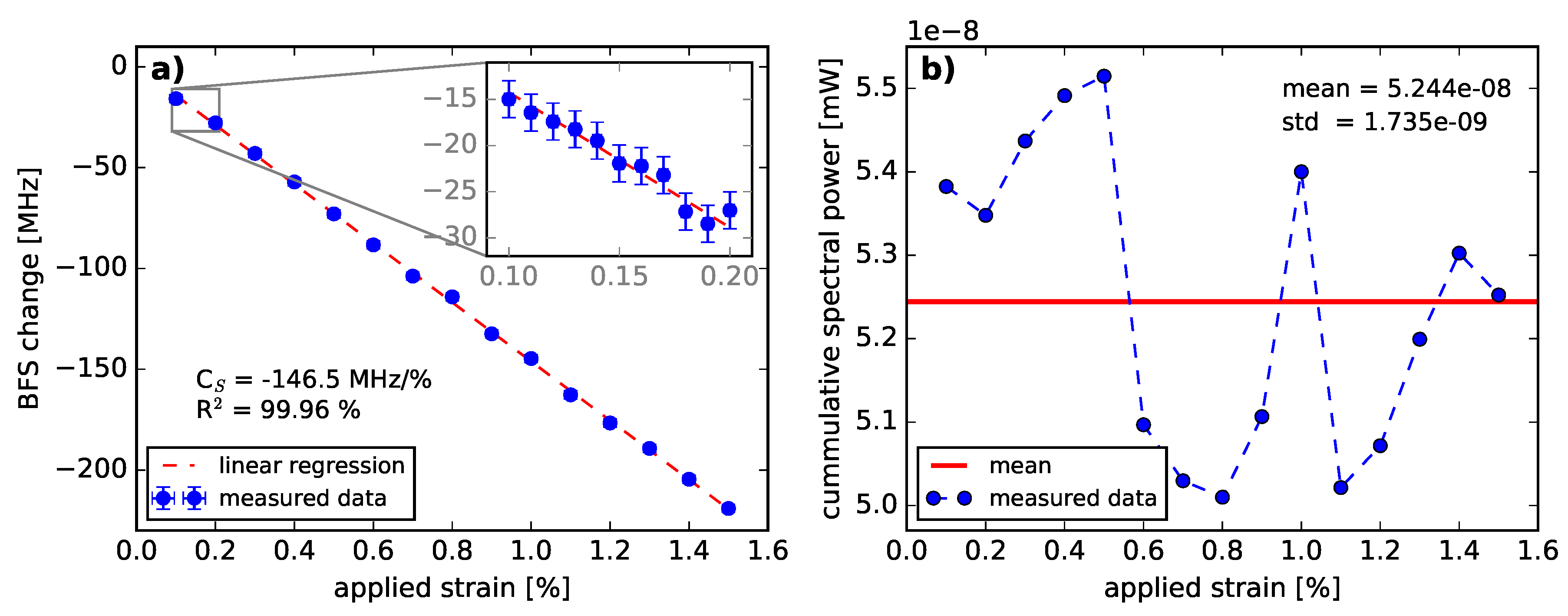
3.1. Brillouin Linewidth and Backscattering Power
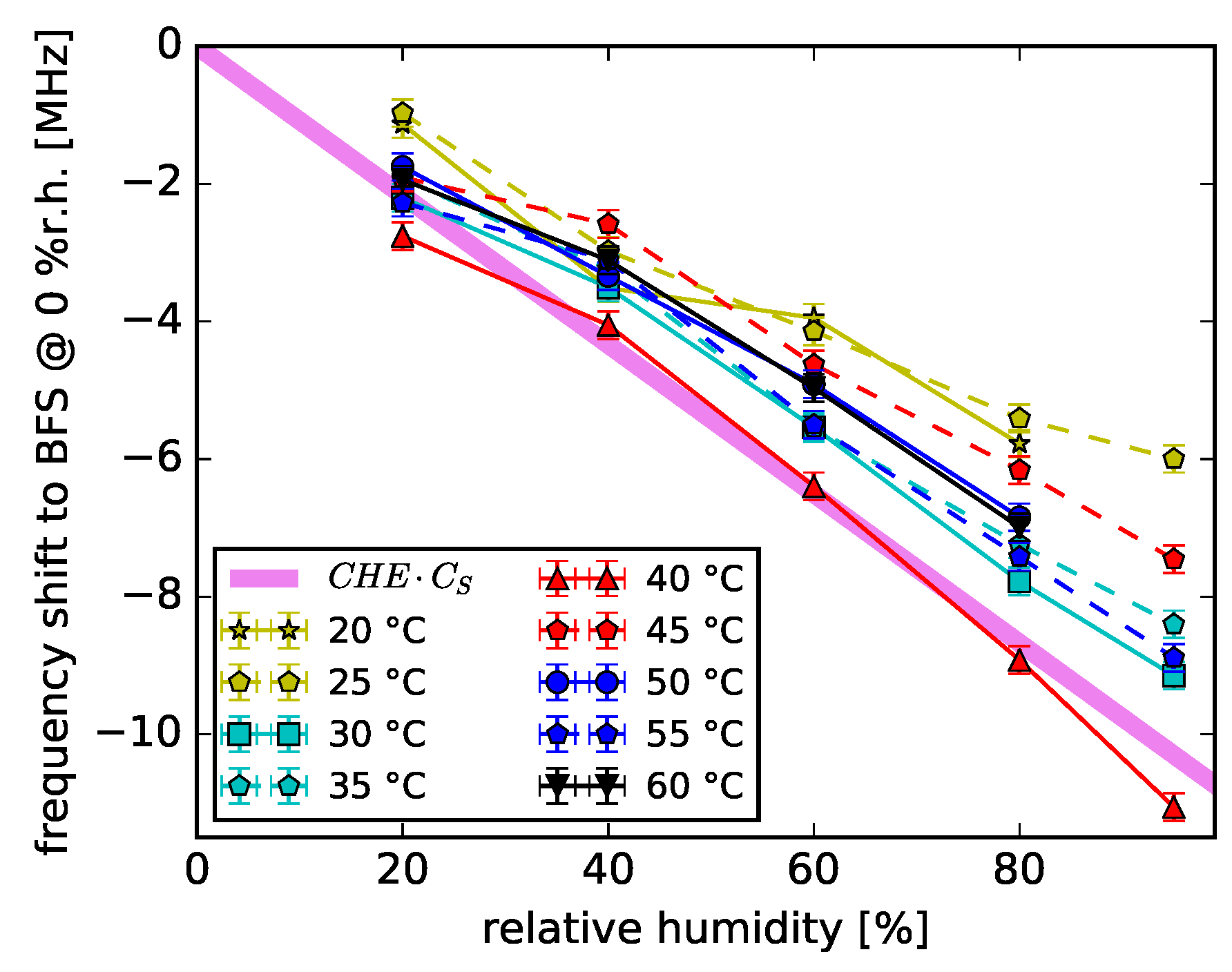
3.2. Brillouin Frequency Shift
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| POF | polymer optical fiber |
| PMMA | polymethylmethacrylate |
| PMMA-POF | POF based on PMMA |
| POFBG | polymer optical fiber Bragg grating |
| PFGI-POF | perfluorinated graded-index POF |
| CYTOP | cyclic transparent optical polymer |
| BFS | Brillouin frequency shift |
| SBS | stimulated Brillouin scattering |
| OSA | optical spectrum analyzer |
| BGS | Brillouin gain spectrum |
| CHE | coefficient of hygroscopic expansion |
| CTE | coefficient of thermal expansion |
References
- Bair, H.; Johnson, G.; Merriweather, R. Water sorption of polycarbonate and its effect on the polymers dielectric behavior. J. Appl. Phys. 1978, 49, 4976–4984. [Google Scholar] [CrossRef]
- Ito, E.; Kobayashi, Y. Changes in physical properties of polycarbonate by absorbed water. J. Appl. Polym. Sci. 1978, 22, 1143–1149. [Google Scholar] [CrossRef]
- Watanabe, T.; Ooba, N.; Hida, Y.; Hikita, M. Influence of humidity on refractive index of polymers for optical waveguide and its temperature dependence. Appl. Phys. Lett. 1998, 72, 1533–1535. [Google Scholar] [CrossRef]
- Weitsman, Y.J. Fluid Effects in Polymers and Polymeric Composites; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Doǧan, A.; Bek, B.; Cevik, N.; Usanmaz, A. The effect of preparation conditions of acrylic denture base materials on the level of residual monomer, mechanical properties and water absorption. J. Dent. 1995, 23, 313–318. [Google Scholar] [CrossRef]
- Muto, S.; Suzuki, O.; Amano, T.; Morisawa, M. A plastic optical fibre sensor for real-time humidity monitoring. Meas. Sci. Technol. 2003, 14, 746. [Google Scholar] [CrossRef]
- Leal-Junior, A.; Frizera-Neto, A.; Marques, C.; Pontes, M.J. Measurement of temperature and relative humidity with polymer optical fiber sensors based on the induced stress-optic effect. Sensors 2018, 18, 916. [Google Scholar] [CrossRef] [PubMed]
- Lenke, P.; Wendt, M.; Liehr, S.; Krebber, K. Distributed humidity sensing based on Rayleigh scattering in polymer optical fibers. Proc. SPIE 2010, 7653, 7653–7656. [Google Scholar]
- Liehr, S.; Breithaupt, M.; Krebber, K. Distributed humidity sensing in PMMA optical fibers at 500 nm and 650 nm wavelengths. Sensors 2017, 17, 738. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Webb, D.J.; Peng, G.D. Investigation into time response of polymer fiber Bragg grating based humidity sensors. J. Lightwave Technol. 2012, 30, 1090–1096. [Google Scholar] [CrossRef]
- Bundalo, I.L.; Nielsen, K.; Markos, C.; Bang, O. Bragg grating writing in PMMA microstructured polymer optical fibers in less than 7 minutes. Opt. Express 2014, 22, 5270–5276. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Yan, B.; Zhang, Q.; Peng, G.D.; Wen, J.; Zhang, J. Fabrication of polymer optical fibre (POF) gratings. Sensors 2017, 17, 511. [Google Scholar] [CrossRef] [PubMed]
- Koike, Y. Fundamentals of Plastic Optical Fibers; John Wiley & Sons.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Liehr, S.; Nöther, N.; Krebber, K. Incoherent optical frequency domain reflectometry and distributed strain detection in polymer optical fibers. Meas. Sci. Technol. 2009, 21, 017001. [Google Scholar] [CrossRef]
- Hayashi, N.; Mizuno, Y.; Nakamura, K. Distributed Brillouin sensing with centimeter-order spatial resolution in polymer optical fibers. J. Lightwave Technol. 2014, 32, 3397–3401. [Google Scholar] [CrossRef]
- Liehr, S. Fibre Optic Sensing Techniques Based on Incoherent Optical Frequency Domain Reflectometry; BAM-Dissertationsreihe: Berlin, Germany, 2015. [Google Scholar]
- Lee, H.; Hayashi, N.; Mizuno, Y.; Nakamura, K. Slope-assisted Brillouin optical correlation-domain reflectometry using polymer optical fibers with high propagation loss. J. Lightwave Technol. 2017, 35, 2306–2310. [Google Scholar] [CrossRef]
- Theodosiou, A.; Komodromos, M.; Kalli, K. Carbon cantilever beam health inspection using a polymer fiber Bragg grating array. J. Lightwave Technol. 2018, 36, 986–992. [Google Scholar] [CrossRef]
- Lethien, C.; Loyez, C.; Vilcot, J.P.; Rolland, N.; Rolland, P.A. Exploit the bandwidth capacities of the perfluorinated graded index polymer optical fiber for multi-services distribution. Polymers 2011, 3, 1006–1028. [Google Scholar] [CrossRef]
- Shao, Y.; Cao, R.; Huang, Y.K.; Ji, P.N.; Zhang, S. 112-Gb/s transmission over 100 m of graded-index plastic optical fiber for optical data center applications. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 4–8 March 2012; p. OW3J-5. [Google Scholar]
- Matsuura, M.; Furukawa, R.; Matsumoto, Y.; Inoue, A.; Koike, Y. Evaluation of modal noise in graded-index silica and plastic optical fiber links for radio over multimode fiber systems. Opt. Express 2014, 22, 6562–6568. [Google Scholar] [CrossRef] [PubMed]
- Koike, Y.; Inoue, A. High-speed graded-index plastic optical fibers and their simple interconnects for 4K/8K video transmission. J. Lightwave Technol. 2016, 34, 1551–1555. [Google Scholar] [CrossRef]
- Min, R.; Ortega, B.; Leal-Junior, A.; Marques, C. Fabrication and characterization of Bragg grating in CYTOP POF at 600-nm wavelength. IEEE Sens. Lett. 2018, 2, 1–4. [Google Scholar] [CrossRef]
- Schreier, A.; Wosniok, A.; Liehr, S.; Krebber, K. Humidity-induced Brillouin frequency shift in perfluorinated polymer optical fibers. Opt. Express 2018, 26, 22307–22314. [Google Scholar] [CrossRef] [PubMed]
- Thorlabs. Graded-Index Polymer Optical Fiber (GI-POF). Available online: https://www.thorlabs.com/catalogPages/1100.pdf (accessed on 15 November 2018).
- Schreier, A.; Jeschke, T.; Petermann, K.; Wosniok, A.; Krebber, K. Analytical model for mode based insertion loss in ball-lensed coupling of graded-index silica and polymer fibres. In Proceedings of the 26th International Conference on Plastic Optical Fibres, POF 2017, Aveiro, Portugal, 13–15 September 2017; p. 30. [Google Scholar]
- Rothman, L.; Gordon, I.; Barbe, A.; Benner, D.; Bernath, P.; Birk, M.; Boudon, V.; Brown, L.; Campargue, A.; Champion, J.P.; et al. The HITRAN 2008 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transfer 2009, 110, 533–572. [Google Scholar] [CrossRef] [Green Version]
- O’Hagan, D. Understanding organofluorine chemistry. An introduction to the C–F bond. Chem. Soc. Rev. 2008, 37, 308–319. [Google Scholar] [CrossRef] [PubMed]
- Spießberger, S.; Schiemangk, M.; Wicht, A.; Wenzel, H.; Erbert, G.; Tränkle, G. DBR laser diodes emitting near 1064 nm with a narrow intrinsic linewidth of 2 kHz. Appl. Phys. B 2011, 104, 813. [Google Scholar] [CrossRef]
- Klehr, A.; Sumpf, B.; Hasler, K.H.; Fricke, J.; Liero, A.; Erbert, G. High-power pulse generation in GHz range with 1064 nm DBR tapered laser. IEEE Photonics Technol. Lett. 2010, 22, 832–834. [Google Scholar] [CrossRef]
- Atkins, P.; de Paula, J. Atkins’ Physical Chemistry; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Dong, Y.; Xu, P.; Zhang, H.; Lu, Z.; Chen, L.; Bao, X. Characterization of evolution of mode coupling in a graded-index polymer optical fiber by using Brillouin optical time-domain analysis. Opt. Express 2014, 22, 26510–26516. [Google Scholar] [CrossRef] [PubMed]
- Reshef, O.; Shtyrkova, K.; Moebius, M.G.; Griesse-Nascimento, S.; Spector, S.; Evans, C.C.; Ippen, E.; Mazur, E. Polycrystalline anatase titanium dioxide microring resonators with negative thermo-optic coefficient. J. Opt. Soc. Am. B: Opt. Phys. 2015, 32, 2288–2293. [Google Scholar] [CrossRef]
- Thomas, P.J.; Hellevang, J.O. A fully distributed fibre optic sensor for relative humidity measurements. Sens. Actuators B 2017, 247, 284–289. [Google Scholar] [CrossRef]
- Thomas, P.J.; Hellevang, J.O. A high response polyimide fiber optic sensor for distributed humidity measurements. Sens. Actuators B 2018, 270, 417–423. [Google Scholar] [CrossRef]
- Mizuno, Y.; Ishigure, T.; Nakamura, K. Brillouin gain spectrum characterization in perfluorinated graded-index polymer optical fiber with 62.5 μm core diameter. IEEE Photonics Technol. Lett. 2011, 23, 1863–1865. [Google Scholar] [CrossRef]
- Nikles, M.; Thevenaz, L.; Robert, P.A. Brillouin gain spectrum characterization in single-mode optical fibers. J. Lightwave Technol. 1997, 15, 1842–1851. [Google Scholar] [CrossRef] [Green Version]
- Shenoy, A. Thermoplastic Melt Rheology and Processing; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Stajanca, P.; Cetinkaya, O.; Schukar, M.; Mergo, P.; Webb, D.J.; Krebber, K. Molecular alignment relaxation in polymer optical fibers for sensing applications. Opt. Fiber Technol. 2016, 28, 11–17. [Google Scholar] [CrossRef] [Green Version]
- Leal-Junior, A.G.; Theodosiou, A.; Marques, C.; Pontes, M.J.; Kalli, K.; Frizera, A. Compensation method for temperature cross-sensitivity in transverse force applications with FBG sensors in POFs. J. Lightwave Technol. 2018, 36, 3660–3665. [Google Scholar] [CrossRef]
- Minakawa, K.; Mizuno, Y.; Nakamura, K. Cross effect of strain and temperature on Brillouin frequency shift in polymer optical fibers. J. Lightwave Technol. 2017, 35, 2481–2486. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics; Academic Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Brillouin, L. Diffusion de la lumière et des rayons X par un corps transparent homogène - Influence de l’agitation thermique. Annales de Physique 1922, 9, 88–122. [Google Scholar] [CrossRef]
- Ippen, E.; Stolen, R. Stimulated Brillouin scattering in optical fibers. Appl. Phys. Lett. 1972, 21, 539–541. [Google Scholar] [CrossRef]
- Mizuno, Y.; Nakamura, K. Potential of Brillouin scattering in polymer optical fiber for strain-insensitive high-accuracy temperature sensing. Opt. Lett. 2010, 35, 3985–3987. [Google Scholar] [CrossRef] [PubMed]
- Wosniok, A. Untersuchungen zur Unterscheidung der Einflussgrößen Temperatur und Dehnung bei Anwendung der verteilten Brillouin-Sensorik in der Bauwerksüberwachung; Technische Universität Berlin: Berlin, Germany, 2013. [Google Scholar]
- Hayashi, N.; Minakawa, K.; Mizuno, Y.; Nakamura, K. Brillouin frequency shift hopping in polymer optical fiber. Appl. Phys. Lett. 2014, 105, 091113. [Google Scholar] [CrossRef]
- Yuan, W.; Stefani, A.; Bache, M.; Jacobsen, T.; Rose, B.; Herholdt-Rasmussen, N.; Nielsen, F.K.; Andresen, S.; Sørensen, O.B.; Hansen, K.S.; Bang, O. Improved thermal and strain performance of annealed polymer optical fiber Bragg gratings. Opt. Commun. 2011, 284, 176–182. [Google Scholar] [CrossRef] [Green Version]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schreier, A.; Liehr, S.; Wosniok, A.; Krebber, K. Investigation on the Influence of Humidity on Stimulated Brillouin Backscattering in Perfluorinated Polymer Optical Fibers. Sensors 2018, 18, 3952. https://doi.org/10.3390/s18113952
Schreier A, Liehr S, Wosniok A, Krebber K. Investigation on the Influence of Humidity on Stimulated Brillouin Backscattering in Perfluorinated Polymer Optical Fibers. Sensors. 2018; 18(11):3952. https://doi.org/10.3390/s18113952
Chicago/Turabian StyleSchreier, Andy, Sascha Liehr, Aleksander Wosniok, and Katerina Krebber. 2018. "Investigation on the Influence of Humidity on Stimulated Brillouin Backscattering in Perfluorinated Polymer Optical Fibers" Sensors 18, no. 11: 3952. https://doi.org/10.3390/s18113952
APA StyleSchreier, A., Liehr, S., Wosniok, A., & Krebber, K. (2018). Investigation on the Influence of Humidity on Stimulated Brillouin Backscattering in Perfluorinated Polymer Optical Fibers. Sensors, 18(11), 3952. https://doi.org/10.3390/s18113952




