An EigenECG Network Approach Based on PCANet for Personal Identification from ECG Signal
Abstract
:1. Introduction
Motivation and Contribution
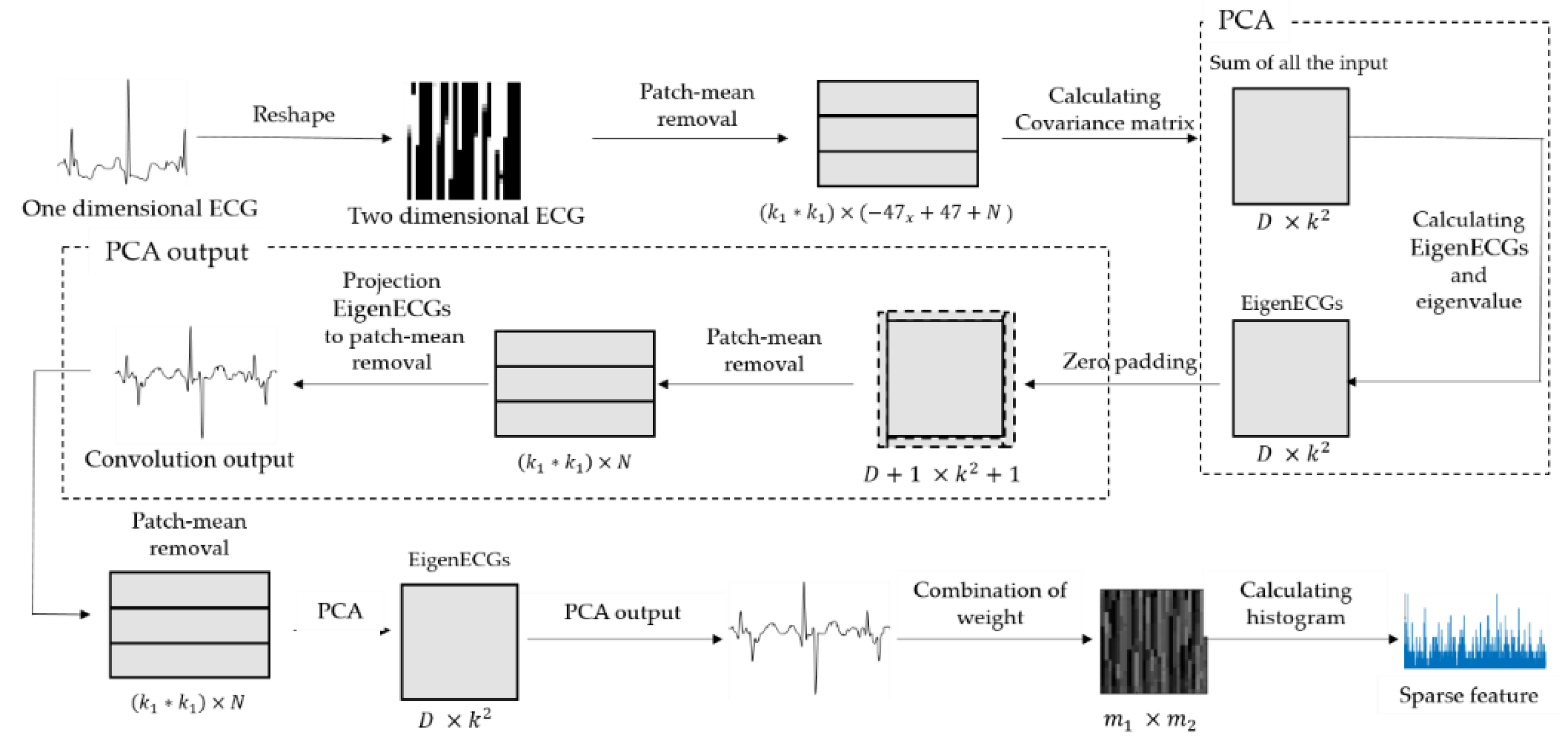
2. PCANet
2.1. PCA
| Algorithm 1 PCA |
| Input: A D-dimensional training set and the new (lower) dimensionality d (with d D)
|
2.2. PCANet
2.2.1. First Stage of PCANet
2.2.2. Second Stage of PCANet
2.2.3. Output Stage of PCANet
2.3. Comparison of PCA with EigenECGs Network (EECGNet)
3. ECG Biometrics Based on EECGNet
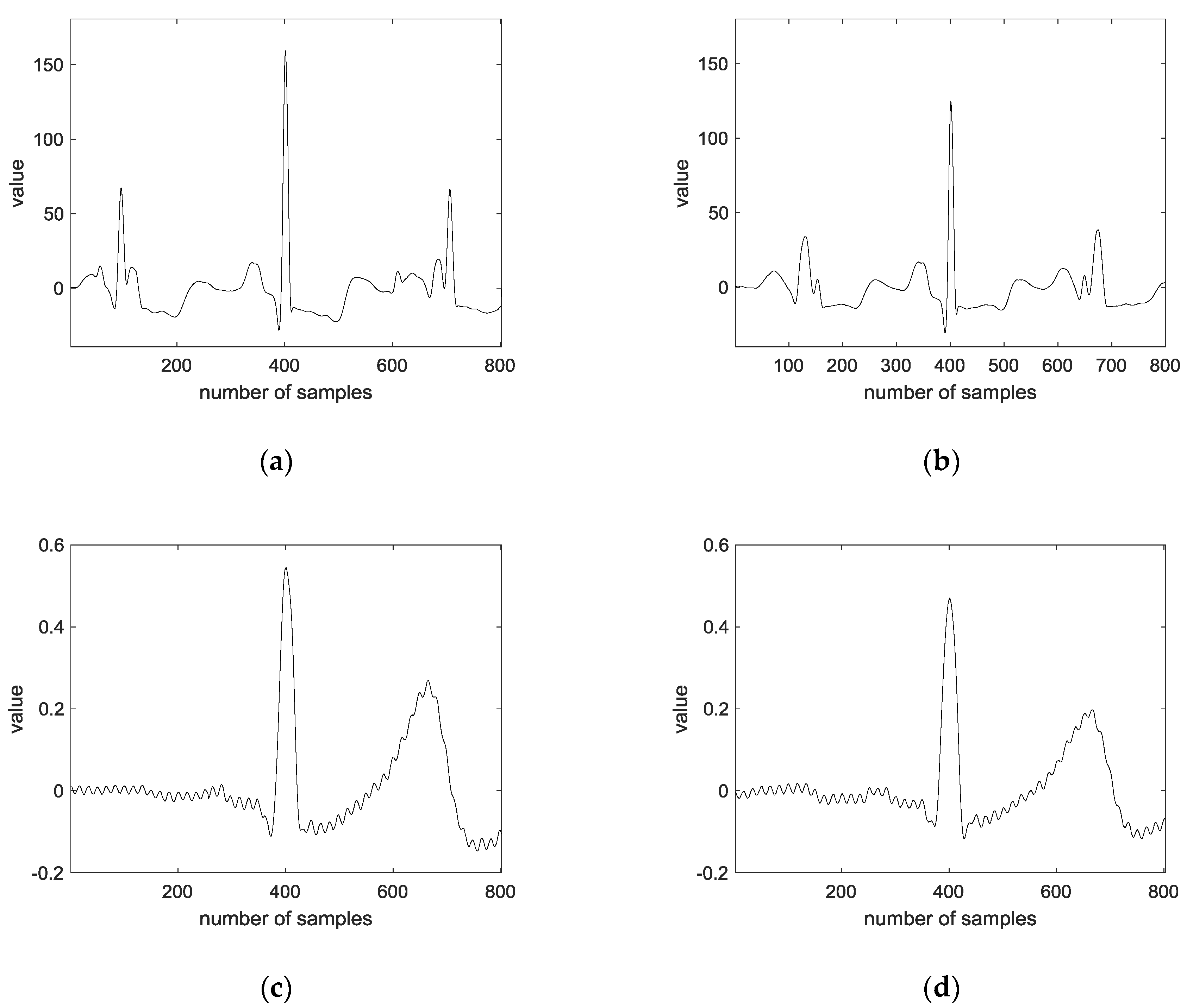
3.1. Preprocessing
- Step 1:
- Convolution is performed on the original signal with an average filter of size 500, and the average convoluted signal is subtracted from the original signal.
- Step 2:
- Convolution is performed with an average filter of size 10 for the regular signal.
- Step 3:
- The largest value in the signal is detected.
- Step 4:
- An average of 400 frames are extracted based on the peaks of both sides.
- Step 5:
- The ECG average signal of one lead and two leads are connected.
3.2. EECGNet-Based ECG Biometrics
| Algorithm 2 EECGNet |
Input: training data
|
4. Experimental Results
4.1. ECG
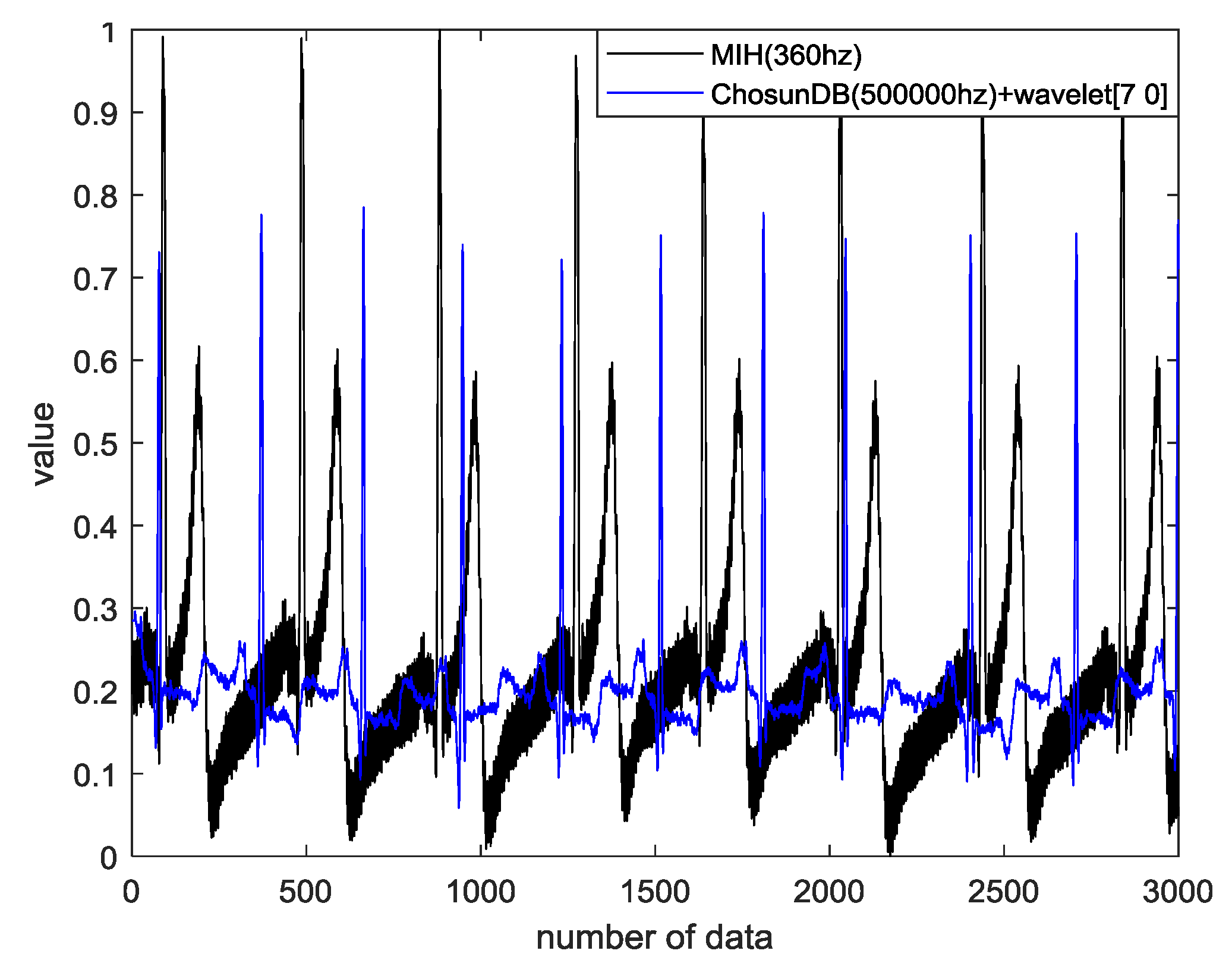
4.2. CU-ECG Database
4.3. MIT-BIH ECG Database
4.4. Data Evaluation and Similarity Measurement
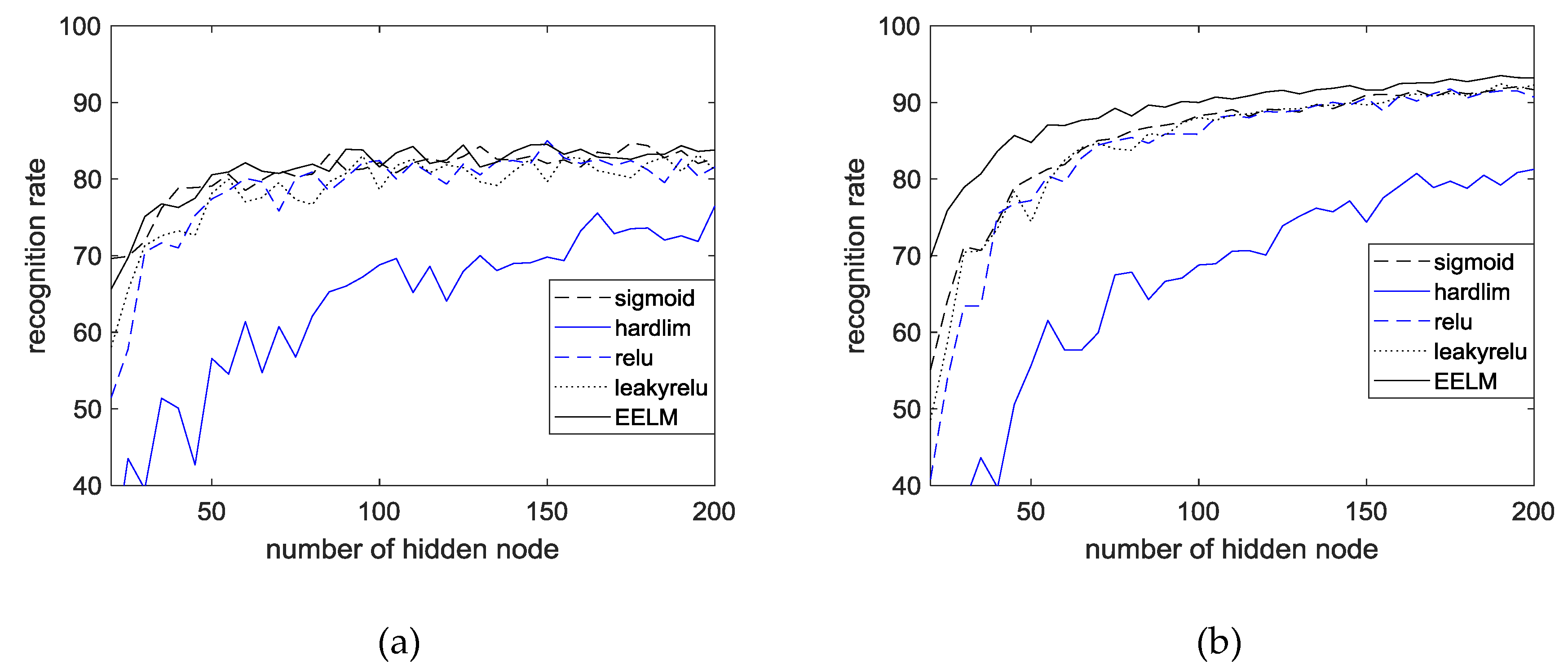
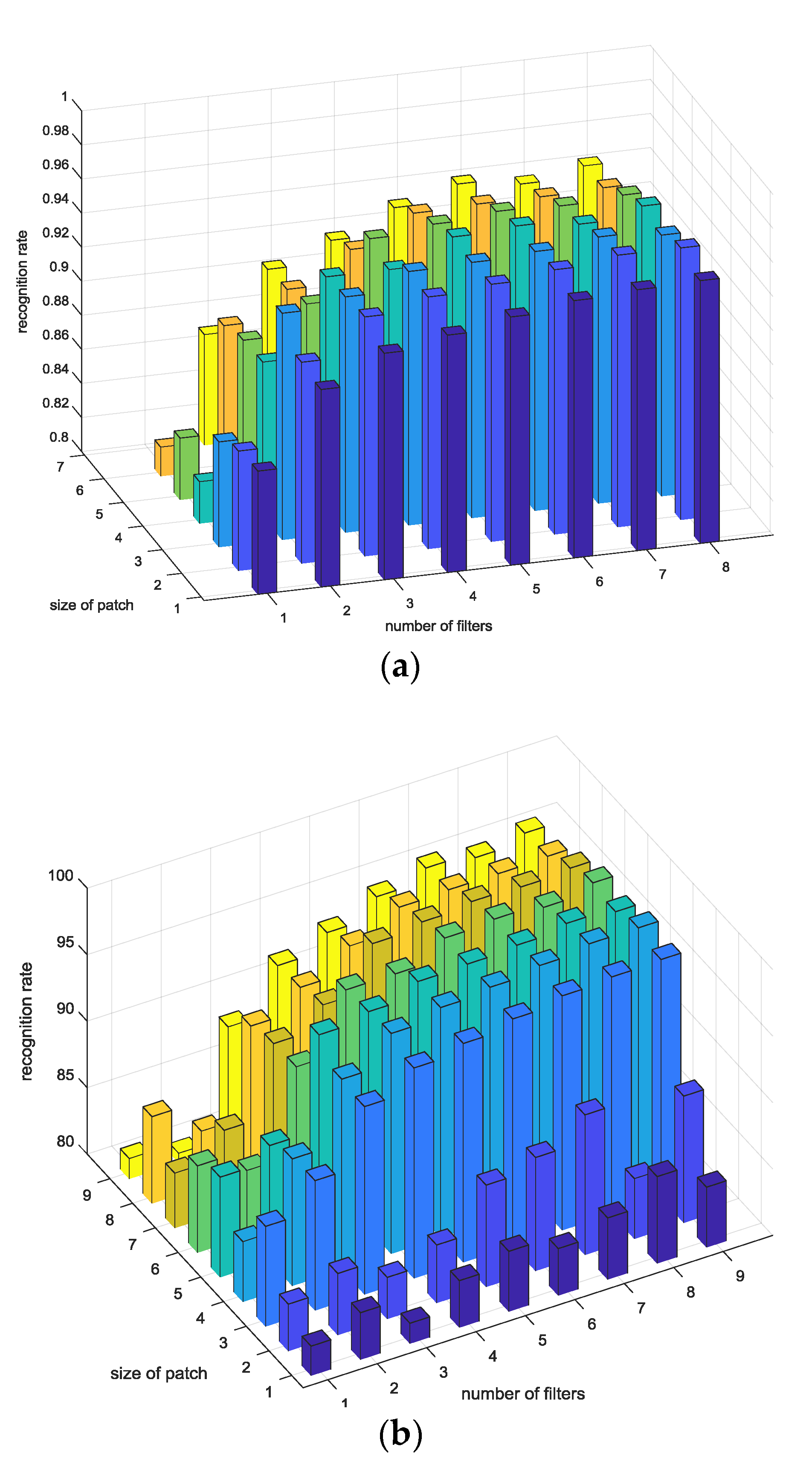
4.5. Performance Evaluation
4.6. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Adam, G.; Witold, P. ECG Signal Processing, Classification and Interpretation; Springer: London, UK, 2012; ISBN 978-0-85729-867-6. [Google Scholar]
- Shadmand, S.; Mashoufi, B. A new personalized ECG signal classification algorithm using block-based neural network and particle swarm optimization. Biomed. Signal. Process. 2016, 25, 12–23. [Google Scholar] [CrossRef]
- Stamos, K.; Naeem, R. DREAMER: A Database for emotion recognition through EEG and ECG signals from wireless low-cost off-the-shelf devices. IEEE J. Biomed. Health Inform. 2018, 22, 98–107. [Google Scholar]
- Rodriguez-Sotelo, J.L.; Cuesta-Frau, D.; Castellanos-Dominguez, G. Unsupervised classification of atrial heartbeats using a prematurity index and wave morphology features. Med. Biol. Eng. Comput. 2009, 47, 731–741. [Google Scholar] [CrossRef] [PubMed]
- Nejadgholi, I.; Moradi, M.H.; Abdolali, F. Using phase space reconstruction for patient independent heartbeat classification in comparison with some benchmark methods. Comput. Biol. Med. 2011, 41, 411–419. [Google Scholar] [CrossRef] [PubMed]
- Wen, C.; Lin, T.C.; Chang, K.C.; Huang, C.H. Classification of ECG complexes using self-organizing CMAC. Measurement 2009, 42, 399–407. [Google Scholar] [CrossRef]
- Yu, S.N.; Chen, Y.H. Noise-tolerant electrocardiogram beat classification based on higher order statistics of subband components. Artif. Intell. Med. 2009, 46, 165–178. [Google Scholar] [CrossRef] [PubMed]
- Kiranyaz, S.; Ince, T.; Pulkkinen, J.; Gabbouj, M. Personalized long-term ECG classification: A systematic approach. Expert Syst. 2011, 38, 3220–3226. [Google Scholar] [CrossRef]
- Long, Z.; Liu, G.; Dai, X. Extracting emotional features from ECG by using wavelet transform. In Proceedings of the 2010 International Conference on Biomedical Engineering and Computer Science, Wuhan, China, 23–25 April 2010; pp. 1–4. [Google Scholar]
- Agrafioti, F.D.; Hatzinakos, A.K. ECG pattern analysis for emotion detection. IEEE Trans. Affect. Comput. 2012, 3, 102–115. [Google Scholar] [CrossRef]
- Tantawi, M.M.; Revett, K.; Salem, A.; Tolba, M.F. Fiducial feature reduction analysis for electrocardiogram (ECG) based biometric recognition. Intell. Inf. Syst. 2013, 40, 17–39. [Google Scholar] [CrossRef]
- Fang, S.C.; Chan, H.L. QRS detection-free electrocardiogram biometrics in the reconstructed phase space. Pattern Recognit. Lett. 2013, 34, 595–602. [Google Scholar] [CrossRef]
- Coutinho, D.P.; Silva, H.; Gamboa, H.; Fred, A.; Figueiredo, M. Novel fiducial and non-fiducial approaches to electrocardiogram-based biometric systems. IET Biom. 2013, 2, 64–75. [Google Scholar] [CrossRef]
- Singh, Y.N.; Gupta, P. Correlation-based classification of heartbeats for individual identification. Soft Comput. 2011, 15, 449–460. [Google Scholar] [CrossRef]
- Odinaka, I.; O’Sullivan, J.A.; Sirevaag, E.J.; Rohrbaugh, J.W. Cardiovascular biometrics: Combining mechanical and electrical signals. IEEE Trans. Inf. Forensics Secur. 2015, 10, 16–27. [Google Scholar] [CrossRef]
- Arteaga-Falconi, J.S.; Osman, H.A.; Saddik, A.E. ECG authentication for mobile devices. IEEE Trans. Instrum. Meas. 2016, 65, 591–600. [Google Scholar] [CrossRef]
- Safie, S.I.; Soraghan, J.J.; Petropoulakis, L. Electrocardiogram (ECG) biometric authentication using pulse active ratio (PAR). IEEE Trans. Inf. Forensics Secur. 2011, 6, 1315–1322. [Google Scholar] [CrossRef]
- Juan, A.; Hussein, A.O. ECG and fingerprint bimodal authentication. Sustain. Cities Soc. 2018, 40, 274–283. [Google Scholar]
- Yin, Z.; Raffaele, G.; Huimin, L. PEA: Parallel electrocardiogram-based authentication for smart healthcare systems. J. Netw. Comput. Appl. 2018, 117, 10–16. [Google Scholar]
- Deng, M.; Wang, C.; Tang, M.; Zheng, T. PEA: Extracting cardiac dynamics within ECG signal for human identification and cardiovascular diseases classification. Neural Netw. 2018, 100, 70–83. [Google Scholar] [CrossRef] [PubMed]
- Carmen, C.; Pedro, P.; Lorena, G.; Juan, T. PEA: Real-time electrocardiogram streams for continuous authentication. Appl. Soft Comput. 2018, 68, 784–794. [Google Scholar]
- Pedro, P.; Lorena, G.; Carmen, C.; Jose, F. Effect of attacker characterization in ECG-based continuous authentication mechanisms for Internet of Things. Future Gener. Comput. Syst. 2018, 81, 67–77. [Google Scholar]
- Mahsa, A.; Nasim, M.; Mohamad, B.; Shamsollahi, C.J. ECG fiducial point extraction using switching Kalman filter. Comput. Methods Programs Biomed. 2018, 157, 129–136. [Google Scholar] [Green Version]
- Peyman, D.; Amir, H.J. A biometric security scheme for wireless body area networks. J. Inf. Secur. Appl. 2018, 41, 62–74. [Google Scholar]
- Abawajy, J.H.; Kelarev, A.V.; Chowdhury, M. Multistage approach for clustering and classification of ECG data. Comput. Methods Programs Biomed. 2013, 112, 720–730. [Google Scholar] [CrossRef] [PubMed]
- Khalaf, A.F.; Owis, M.I.; Yassine, I.A. A novel technique for cardiac arrhythmia classification using spectral correlation and support vector machines. Expert Syst. 2015, 42, 8361–8368. [Google Scholar] [CrossRef]
- Martis, R.J.; Acharya, U.R.; Min, L.C. ECG beat classification using PCA, LDA ICA and discrete wavelet transform. Biomed. Signal. Process. 2013, 8, 437–448. [Google Scholar] [CrossRef]
- Martis, R.J.; Acharya, U.R.; Mandana, K.M.; Ray, A.K.; Chakraborty, C. Cardiac decision making using higher order spectra. Biomed. Signal. Process. 2013, 8, 193–203. [Google Scholar] [CrossRef]
- Wang, J.S.; Lin, C.W. A k-nearest-neighbor classifier with heart rate variability feature-based transformation algorithm for driving stress recognition. Neurocomputing 2013, 116, 136–143. [Google Scholar] [CrossRef]
- Karimipour, A.; Homaeinezhad, M.R. Real-time electrocardiogram P-QRS-T detection-delineation algorithm based on quality-supported analysis of characteristic templates. Comput. Methods Programs Biomed. 2014, 52, 153–165. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Qiu, S.; Kong, Y.; Jiang, L.; Senhadji, L.; Shu, H. PCANet: An energy perspective. Neurocomputing 2018, 313, 271–287. [Google Scholar] [CrossRef]
- Wang, Z.; Bi, Z.; Wang, C.; Wang, H. Traffic lights recognition based on PCANet. In Proceedings of the 2015 Chinese Automation Congress (CAC), Wuhan, China, 27–29 November 2015; pp. 559–564. [Google Scholar]
- Yang, X.; Liu, W.; Tao, D.; Cheng, J. Canonical correlation analysis networks for two-view image recognition. Inf. Sci. 2017, 385, 338–352. [Google Scholar] [CrossRef]
- Zeng, R.; Wu, J.; Shao, Z.; Chen, Y.; Chen, B.; Senhadji, L.; Shu, H. Color image classification via quaternion principal component analysis. Neurocomputing 2016, 216, 416–428. [Google Scholar] [CrossRef]
- Chan, T.H.; Jia, K.; Gao, S.; Lu, J.; Zeng, Z.; Ma, Y. PCANet: A simple deep learning baseline for image classification? IEEE Trans. Image Process. 2015, 24, 5017–5032. [Google Scholar] [CrossRef] [PubMed]
- Fan, R.E.; Chang, K.W.; Hsieh, C.J.; Wang, X.R.; Lin, C.J. LIBLINEAR: A library for large linear classification. J. Mach. Learn. Res. 2008, 9, 1871–1874. [Google Scholar]
- Merone, M.; Soda, P.; Sansone, M.; Sansone, C. ECG databases for biometric systems: A systematic review. Expert Syst. 2017, 67, 189–202. [Google Scholar] [CrossRef]
- Liu, S.H.; Wang, J.J.; Su, C.H.; Tan, T.H. Development of a patch-type electrocardiographic monitor for real time heartbeat detection and heart rate variability analysis. J. Med. Biol. Eng. 2018, 38, 411–423. [Google Scholar] [CrossRef]
- Diagnostic Electrocardiographic Devices (ANSI/AAMI EC11-1991); Association for the Advancement of Medical Instrumentation: Arlington, VA, USA.












| Parameters | Definition |
|---|---|
| The size of input image | |
| N | The number of data |
| The patch size. are odd integers and satisfy | |
| The number of filters of two stages. | |
| The block size: 1 | |
| The overlap ratio of block. |
| Acc (R = 0.5) | Acc (R = 0.6) | Acc (R = 0.5) | Acc (R = 0.6) | Acc (R = 0.5) | Acc (R = 0.6) | Acc (R = 0.5) | Acc (R = 0.6) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 | 3 | 3 | 92.68 | 94.89 | 8 | 3 | 3 | 92.68 | 92.78 | 10 | 3 | 3 | 92.68 | 92.68 | 12 | 3 | 3 | 92.68 | 92.68 |
| 3 | 4 | 95.50 | 95.52 | 3 | 4 | 95.50 | 95.58 | 3 | 4 | 95.50 | 95.50 | 3 | 4 | 95.50 | 95.50 | ||||
| 3 | 5 | 97.35 | 97.37 | 3 | 5 | 97.35 | 97.38 | 3 | 5 | 97.35 | 97.35 | 3 | 5 | 97.35 | 97.35 | ||||
| 3 | 6 | 97.26 | 97.27 | 3 | 6 | 97.26 | 97.46 | 3 | 6 | 97.26 | 97.26 | 3 | 6 | 97.26 | 97.26 | ||||
| 3 | 7 | 96.98 | 96.99 | 3 | 7 | 96.98 | 96.99 | 3 | 7 | 96.98 | 96.98 | 3 | 7 | 96.98 | 96.98 | ||||
| 3 | 8 | 96.82 | 96.92 | 3 | 8 | 96.82 | 96.88 | 3 | 8 | 96.82 | 96.82 | 3 | 8 | 92.82 | 96.82 | ||||
| 3 | 9 | 96.77 | 96.97 | 3 | 9 | 96.61 | 96.79 | 3 | 9 | 96.67 | 96.77 | 3 | 9 | 96.77 | 96.77 | ||||
| 4 | 3 | 94.46 | 94.66 | 4 | 3 | 94.46 | 94.48 | 4 | 3 | 94.46 | 94.46 | 4 | 3 | 94.46 | 94.46 | ||||
| 4 | 4 | 96.39 | 96.79 | 4 | 4 | 96.39 | 96.49 | 4 | 4 | 96.39 | 96.39 | 4 | 4 | 96.39 | 96.39 | ||||
| 4 | 5 | 97.27 | 97.47 | 4 | 5 | 97.27 | 97.67 | 4 | 5 | 97.27 | 97.27 | 4 | 5 | 97.27 | 97.27 | ||||
| 4 | 6 | 97.74 | 97.84 | 4 | 6 | 97.74 | 97.84 | 4 | 6 | 97.74 | 97.84 | 4 | 6 | 97.74 | 97.94 | ||||
| 4 | 7 | 98.19 | 98.69 | 4 | 7 | 98.19 | 98.59 | 4 | 7 | 98.19 | 98.69 | 4 | 7 | 98.19 | 98.89 | ||||
| 4 | 8 | 98.00 | 98.20 | 4 | 8 | 98.00 | 98.20 | 4 | 8 | 98.00 | 98.50 | 4 | 8 | 98.00 | 98.50 | ||||
| 4 | 9 | 98.09 | 98.59 | 4 | 9 | 98.09 | 98.39 | 4 | 9 | 98.09 | 98.39 | 4 | 9 | 98.09 | 98.79 | ||||
| 5 | 3 | 95.52 | 95.62 | 5 | 3 | 95.52 | 95.82 | 5 | 3 | 95.52 | 95.62 | 5 | 3 | 95.52 | 95.92 | ||||
| 5 | 4 | 96.42 | 96.72 | 5 | 4 | 96.42 | 96.62 | 5 | 4 | 96.12 | 96.62 | 5 | 4 | 96.42 | 96.72 | ||||
| 5 | 5 | 97.20 | 97.60 | 5 | 5 | 97.20 | 97.40 | 5 | 5 | 97.20 | 97.50 | 5 | 5 | 97.20 | 97.50 | ||||
| 5 | 6 | 97.77 | 97.87 | 5 | 6 | 97.77 | 97.97 | 5 | 6 | 97.77 | 97.87 | 5 | 6 | 97.77 | 97.97 | ||||
| 5 | 7 | 97.95 | 97.98 | 5 | 7 | 97.95 | 97.99 | 5 | 7 | 97.95 | 98.15 | 5 | 7 | 97.95 | 98.15 | ||||
| 5 | 8 | 98.14 | 98.16 | 5 | 8 | 98.14 | 98.15 | 5 | 8 | 98.14 | 98.34 | 5 | 8 | 98.14 | 98.64 | ||||
| 5 | 9 | 98.21 | 98.28 | 5 | 9 | 98.21 | 98.24 | 5 | 9 | 98.21 | 98.31 | 5 | 9 | 98.21 | 98.71 | ||||
| 6 | 3 | 94.80 | 94.88 | 6 | 3 | 94.80 | 94.88 | 6 | 3 | 94.80 | 95.30 | 6 | 3 | 94.80 | 94.80 | ||||
| 6 | 4 | 96.78 | 96.79 | 6 | 4 | 96.78 | 96.79 | 6 | 4 | 96.78 | 97.28 | 6 | 4 | 96.78 | 96.98 | ||||
| 6 | 5 | 97.31 | 97.61 | 6 | 5 | 97.31 | 97.35 | 6 | 5 | 97.31 | 98.11 | 6 | 5 | 97.31 | 97.71 | ||||
| 6 | 6 | 97.43 | 97.63 | 6 | 6 | 97.43 | 97.63 | 6 | 6 | 97.43 | 97.63 | 6 | 6 | 97.43 | 97.43 | ||||
| 6 | 7 | 98.02 | 98.72 | 6 | 7 | 98.02 | 98.72 | 6 | 7 | 98.02 | 98.32 | 6 | 7 | 98.02 | 98.05 | ||||
| 6 | 8 | 98.26 | 98.36 | 6 | 8 | 98.02 | 98.56 | 6 | 8 | 98.02 | 98.56 | 6 | 8 | 98.26 | 98.27 | ||||
| 6 | 9 | 93.30 | 93.41 | 6 | 9 | 98.26 | 93.60 | 6 | 9 | 98.26 | 93.40 | 6 | 9 | 93.30 | 93.39 | ||||
| 7 | 3 | 96.08 | 96.28 | 7 | 3 | 93.30 | 96.88 | 7 | 3 | 93.30 | 96.58 | 7 | 3 | 96.08 | 96.58 | ||||
| 7 | 4 | 97.19 | 97.69 | 7 | 4 | 96.08 | 97.49 | 7 | 4 | 96.08 | 97.39 | 7 | 4 | 97.19 | 97.39 | ||||
| 7 | 5 | 97.68 | 97.78 | 7 | 5 | 97.19 | 97.88 | 7 | 5 | 97.19 | 97.78 | 7 | 5 | 97.68 | 97.78 | ||||
| 7 | 6 | 97.95 | 97.96 | 7 | 6 | 97.68 | 98.15 | 7 | 6 | 97.68 | 98.15 | 7 | 6 | 97.95 | 97.98 | ||||
| 7 | 7 | 97.96 | 97.98 | 7 | 7 | 97.95 | 97.99 | 7 | 7 | 97.95 | 97.99 | 7 | 7 | 97.96 | 9799 | ||||
| 7 | 8 | 98.01 | 98.06 | 7 | 8 | 97.96 | 98.09 | 7 | 8 | 97.96 | 98.05 | 7 | 8 | 98.01 | 98.05 | ||||
| 7 | 9 | 92.97 | 92.99 | 7 | 9 | 98.01 | 92.99 | 7 | 9 | 98.01 | 92.99 | 7 | 9 | 92.97 | 92.99 | ||||
| 8 | 3 | 95.11 | 95.21 | 8 | 3 | 92.97 | 95.61 | 8 | 3 | 92.97 | 95.16 | 8 | 3 | 95.11 | 95.12 | ||||
| 8 | 4 | 96.62 | 96.72 | 8 | 4 | 95.11 | 96.82 | 8 | 4 | 95.11 | 96.68 | 8 | 4 | 96.62 | 96.72 | ||||
| 8 | 5 | 97.08 | 97.88 | 8 | 5 | 96.62 | 97.58 | 8 | 5 | 96.62 | 97.38 | 8 | 5 | 97.08 | 97.78 | ||||
| 8 | 6 | 97.57 | 97.77 | 8 | 6 | 97.08 | 97.87 | 8 | 6 | 97.08 | 97.67 | 8 | 6 | 97.57 | 97.58 | ||||
| 8 | 7 | 97.65 | 97.85 | 8 | 7 | 97.57 | 98.15 | 8 | 7 | 97.57 | 97.68 | 8 | 7 | 97.65 | 97.68 | ||||
| 8 | 8 | 97.86 | 97.96 | 8 | 8 | 97.65 | 97.86 | 8 | 8 | 97.65 | 97.96 | 8 | 8 | 97.86 | 97.89 | ||||
| 8 | 9 | 92.18 | 92.38 | 8 | 9 | 97.86 | 92.98 | 8 | 9 | 97.86 | 92.38 | 8 | 9 | 92.18 | 92.19 | ||||
| 9 | 3 | 94.23 | 94.53 | 9 | 3 | 92.18 | 94.63 | 9 | 3 | 92.18 | 94.26 | 9 | 3 | 94.23 | 94.29 | ||||
| 9 | 4 | 96.74 | 96.84 | 9 | 4 | 94.23 | 96.94 | 9 | 4 | 94.23 | 96.79 | 9 | 4 | 96.74 | 96.79 | ||||
| 9 | 5 | 96.98 | 96.99 | 9 | 5 | 96.74 | 97.68 | 9 | 5 | 94.74 | 97.98 | 9 | 5 | 96.98 | 96.99 | ||||
| 9 | 6 | 91.57 | 91.77 | 9 | 6 | 96.98 | 91.67 | 9 | 6 | 96.98 | 91.47 | 9 | 6 | 91.57 | 91.67 | ||||
| 9 | 7 | 97.46 | 98.11 | 9 | 7 | 97.46 | 97.66 | 9 | 7 | 97.46 | 97.66 | 9 | 7 | 97.46 | 97.76 | ||||
| 9 | 8 | 97.54 | 97.58 | 9 | 8 | 97.46 | 97.84 | 9 | 8 | 97.46 | 97.58 | 9 | 8 | 97.54 | 97.84 | ||||
| 9 | 9 | 97.54 | 98.14 | 9 | 9 | 97.54 | 97.74 | 9 | 9 | 97.54 | 97.84 | 9 | 9 | 97.54 | 97.94 |
| Acc (R = 0.5) | Acc (R = 0.6) | Acc (R = 0.5) | Acc (R = 0.6) | Acc (R = 0.5) | Acc (R = 0.6) | Acc (R = 0.5) | Acc (R = 0.6) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 | 3 | 3 | 91.60 | 92.23 | 8 | 3 | 3 | 90.00 | 91.06 | 10 | 3 | 3 | 88.51 | 88.94 | 12 | 3 | 3 | 86.49 | 88.72 |
| 3 | 4 | 92.98 | 93.19 | 3 | 4 | 93.09 | 93.30 | 3 | 4 | 92.23 | 92.87 | 3 | 4 | 90.21 | 92.77 | ||||
| 3 | 5 | 94.57 | 94.15 | 3 | 5 | 93.62 | 94.47 | 3 | 5 | 93.93 | 94.57 | 3 | 5 | 93.40 | 94.15 | ||||
| 3 | 6 | 94.68 | 94.89 | 3 | 6 | 94.89 | 95.00 | 3 | 6 | 94.36 | 94.68 | 3 | 6 | 94.47 | 95.00 | ||||
| 3 | 7 | 95.00 | 95.43 | 3 | 7 | 95.53 | 95.74 | 3 | 7 | 95.21 | 95.85 | 3 | 7 | 95.43 | 95.53 | ||||
| 3 | 8 | 95.53 | 95.64 | 3 | 8 | 95.11 | 95.43 | 3 | 8 | 95.64 | 95.85 | 3 | 8 | 95.21 | 95.85 | ||||
| 3 | 9 | 95.32 | 95.43 | 3 | 9 | 95.11 | 95.21 | 3 | 9 | 95.21 | 95.53 | 3 | 9 | 95.96 | 95.43 | ||||
| 4 | 3 | 92.34 | 92.34 | 4 | 3 | 90.96 | 91.06 | 4 | 3 | 88.62 | 89.68 | 4 | 3 | 86.60 | 89.15 | ||||
| 4 | 4 | 94.26 | 92.93 | 4 | 4 | 93.51 | 93.72 | 4 | 4 | 92.66 | 92.77 | 4 | 4 | 90.85 | 92.13 | ||||
| 4 | 5 | 95.00 | 95.11 | 4 | 5 | 94.26 | 94.89 | 4 | 5 | 94.15 | 94.57 | 4 | 5 | 93.94 | 94.26 | ||||
| 4 | 6 | 95.32 | 95.64 | 4 | 6 | 94.89 | 95.43 | 4 | 6 | 95.00 | 95.11 | 4 | 6 | 94.68 | 95.00 | ||||
| 4 | 7 | 95.32 | 95.43 | 4 | 7 | 95.53 | 95.32 | 4 | 7 | 95.64 | 95.53 | 4 | 7 | 95.43 | 95.64 | ||||
| 4 | 8 | 95.85 | 95.74 | 4 | 8 | 95.85 | 95.85 | 4 | 8 | 96.49 | 96.17 | 4 | 8 | 96.28 | 96.38 | ||||
| 4 | 9 | 95.74 | 95.53 | 4 | 9 | 95.64. | 96.06 | 4 | 9 | 96.17 | 95.96 | 4 | 9 | 96.06 | 95.96 | ||||
| 5 | 3 | 93.30 | 92.98 | 5 | 3 | 92.55 | 92.66 | 5 | 3 | 89.47 | 91.70 | 5 | 3 | 88.09 | 89.68 | ||||
| 5 | 4 | 93.51 | 93.62 | 5 | 4 | 92.66 | 93.51 | 5 | 4 | 92.66 | 93.51 | 5 | 4 | 92.13 | 92.66 | ||||
| 5 | 5 | 94.68 | 94.57 | 5 | 5 | 94.79 | 94.36 | 5 | 5 | 94.15 | 94.47 | 5 | 5 | 94.79 | 94.47 | ||||
| 5 | 6 | 95.53 | 94.89 | 5 | 6 | 95.32 | 95.21 | 5 | 6 | 95.32 | 95.53 | 5 | 6 | 95.32 | 95.21 | ||||
| 5 | 7 | 95.32 | 95.53 | 5 | 7 | 95.64 | 95.32 | 5 | 7 | 95.21 | 95.43 | 5 | 7 | 95.85 | 95.21 | ||||
| 5 | 8 | 95.53 | 95.43 | 5 | 8 | 95.85 | 95.53 | 5 | 8 | 95.64 | 95.64 | 5 | 8 | 96.17 | 96.06 | ||||
| 5 | 9 | 95.64 | 95.32 | 5 | 9 | 95.74 | 95.11 | 5 | 9 | 95.64 | 95.53 | 5 | 9 | 95.53 | 95.43 | ||||
| 6 | 3 | 89.36 | 89.89 | 6 | 3 | 89.47 | 89.68 | 6 | 3 | 87.34 | 89.47 | 6 | 3 | 85.85 | 88.51 | ||||
| 6 | 4 | 93.09 | 93.72 | 6 | 4 | 93.30 | 93.30 | 6 | 4 | 91.70 | 92.77 | 6 | 4 | 90.53 | 92.13 | ||||
| 6 | 5 | 93.09 | 93.83 | 6 | 5 | 93.51 | 94.04 | 6 | 5 | 93.51 | 93.83 | 6 | 5 | 92.77 | 94.36 | ||||
| 6 | 6 | 94.79 | 95.21 | 6 | 6 | 95.21 | 95.00 | 6 | 6 | 94.79 | 95.32 | 6 | 6 | 94.57 | 95.21 | ||||
| 6 | 7 | 95.43 | 95.32 | 6 | 7 | 95.11 | 95.32 | 6 | 7 | 95.64 | 95.3 | 6 | 7 | 95.21 | 95.53 | ||||
| 6 | 8 | 94.89 | 94.89 | 6 | 8 | 95.21 | 95.21 | 6 | 8 | 95.74 | 95.53 | 6 | 8 | 95.64 | 96.06 | ||||
| 6 | 9 | 95.21 | 95.53 | 6 | 9 | 95.64 | 95.64 | 6 | 9 | 95.64 | 95.96 | 6 | 9 | 95.43 | 95.74 | ||||
| 7 | 3 | 89.04 | 89.26 | 7 | 3 | 87.13 | 88.72 | 7 | 3 | 87.23 | 87.13 | 7 | 3 | 85.53 | 86.49 | ||||
| 7 | 4 | 91.28 | 91.49 | 7 | 4 | 91.17 | 90.96 | 7 | 4 | 90.53 | 90.96 | 7 | 4 | 89.79 | 91.06 | ||||
| 7 | 5 | 94.04 | 94.26 | 7 | 5 | 94.04 | 94.36 | 7 | 5 | 93.62 | 93.83 | 7 | 5 | 93.19 | 93.51 | ||||
| 7 | 6 | 94.36 | 94.15 | 7 | 6 | 94.36 | 94.04 | 7 | 6 | 93.40 | 93.72 | 7 | 6 | 93.51 | 93.83 | ||||
| 7 | 7 | 94.57 | 94.89 | 7 | 7 | 95.00 | 95.00 | 7 | 7 | 94.36 | 95.00 | 7 | 7 | 94.47 | 94.57 | ||||
| 7 | 8 | 94.26 | 94.57 | 7 | 8 | 95.11 | 95.43 | 7 | 8 | 95.21 | 95.11 | 7 | 8 | 95.64 | 95.43 | ||||
| 7 | 9 | 94.79 | 94.79 | 7 | 9 | 94.68 | 95.43 | 7 | 9 | 95.74 | 95.64 | 7 | 9 | 95.64 | 95.43 | ||||
| 8 | 3 | 88.40 | 88.83 | 8 | 3 | 87.98 | 88.19 | 8 | 3 | 86.91 | 86.91 | 8 | 3 | 85.00 | 86.70 | ||||
| 8 | 4 | 90.11 | 90.32 | 8 | 4 | 89.57 | 89.04 | 8 | 4 | 88.62 | 88.72 | 8 | 4 | 87.87 | 88.51 | ||||
| 8 | 5 | 92.02 | 92.34 | 8 | 5 | 91.49 | 91.49 | 8 | 5 | 90.53 | 90.96 | 8 | 5 | 90.21 | 91.60 | ||||
| 8 | 6 | 93.40 | 93.40 | 8 | 6 | 93.51 | 93.40 | 8 | 6 | 93.09 | 93.19 | 8 | 6 | 92.02 | 93.40 | ||||
| 8 | 7 | 93.72 | 93.40 | 8 | 7 | 93.19 | 92.87 | 8 | 7 | 92.98 | 93.30 | 8 | 7 | 92.87 | 93.09 | ||||
| 8 | 8 | 93.72 | 93.83 | 8 | 8 | 93.94 | 92.83 | 8 | 8 | 93.83 | 94.04 | 8 | 8 | 93.83 | 94.15 | ||||
| 8 | 9 | 93.72 | 93.51 | 8 | 9 | 93.72 | 92.83 | 8 | 9 | 93.94 | 93.72 | 8 | 9 | 93.94 | 94.57 | ||||
| 9 | 3 | 86.06 | 87.23 | 9 | 3 | 85.96 | 85.43 | 9 | 3 | 84.57 | 85.32 | 9 | 3 | 83.19 | 84.47 | ||||
| 9 | 4 | 90.00 | 90.00 | 9 | 4 | 90.53 | 89.15 | 9 | 4 | 88.19 | 88.62 | 9 | 4 | 87.34 | 88.19 | ||||
| 9 | 5 | 91.06 | 80.85 | 9 | 5 | 90.64 | 91.06 | 9 | 5 | 90.74 | 90.96 | 9 | 5 | 90.32 | 90.74 | ||||
| 9 | 6 | 92.98 | 92.55 | 9 | 6 | 92.23 | 92.23 | 9 | 6 | 92.34 | 91.91 | 9 | 6 | 91.81 | 92.55 | ||||
| 9 | 7 | 93.30 | 93.40 | 9 | 7 | 93.72 | 92.87 | 9 | 7 | 93.19 | 93.09 | 9 | 7 | 92.98 | 92.98 | ||||
| 9 | 8 | 93.09 | 93.51 | 9 | 8 | 93.19 | 93.19 | 9 | 8 | 92.66 | 93.09 | 9 | 8 | 93.09 | 93.51 | ||||
| 9 | 9 | 93.62 | 93.94 | 9 | 9 | 95.51 | 93.51 | 9 | 9 | 93.94 | 93.62 | 9 | 9 | 93.72 | 94.04 |
| Algorithm | PCA | ELM | EELM | AE | EECGNet | |
|---|---|---|---|---|---|---|
| Database | ||||||
| MIT-BIH ECG database | 90.82% | 85.72% | 87.30% | 91.25% | 96.06% | |
| CU-ECG database | 96.45% | 89.89% | 91.24% | 93.24% | 98.87% | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-N.; Byeon, Y.-H.; Pan, S.-B.; Kwak, K.-C. An EigenECG Network Approach Based on PCANet for Personal Identification from ECG Signal. Sensors 2018, 18, 4024. https://doi.org/10.3390/s18114024
Lee J-N, Byeon Y-H, Pan S-B, Kwak K-C. An EigenECG Network Approach Based on PCANet for Personal Identification from ECG Signal. Sensors. 2018; 18(11):4024. https://doi.org/10.3390/s18114024
Chicago/Turabian StyleLee, Jae-Neung, Yeong-Hyeon Byeon, Sung-Bum Pan, and Keun-Chang Kwak. 2018. "An EigenECG Network Approach Based on PCANet for Personal Identification from ECG Signal" Sensors 18, no. 11: 4024. https://doi.org/10.3390/s18114024
APA StyleLee, J.-N., Byeon, Y.-H., Pan, S.-B., & Kwak, K.-C. (2018). An EigenECG Network Approach Based on PCANet for Personal Identification from ECG Signal. Sensors, 18(11), 4024. https://doi.org/10.3390/s18114024







