Effect of Torsion Stress on the Offset and Sensitivity of Diagonal and Off-Diagonal GMI in Amorphous Wires †
Abstract
:1. Introduction
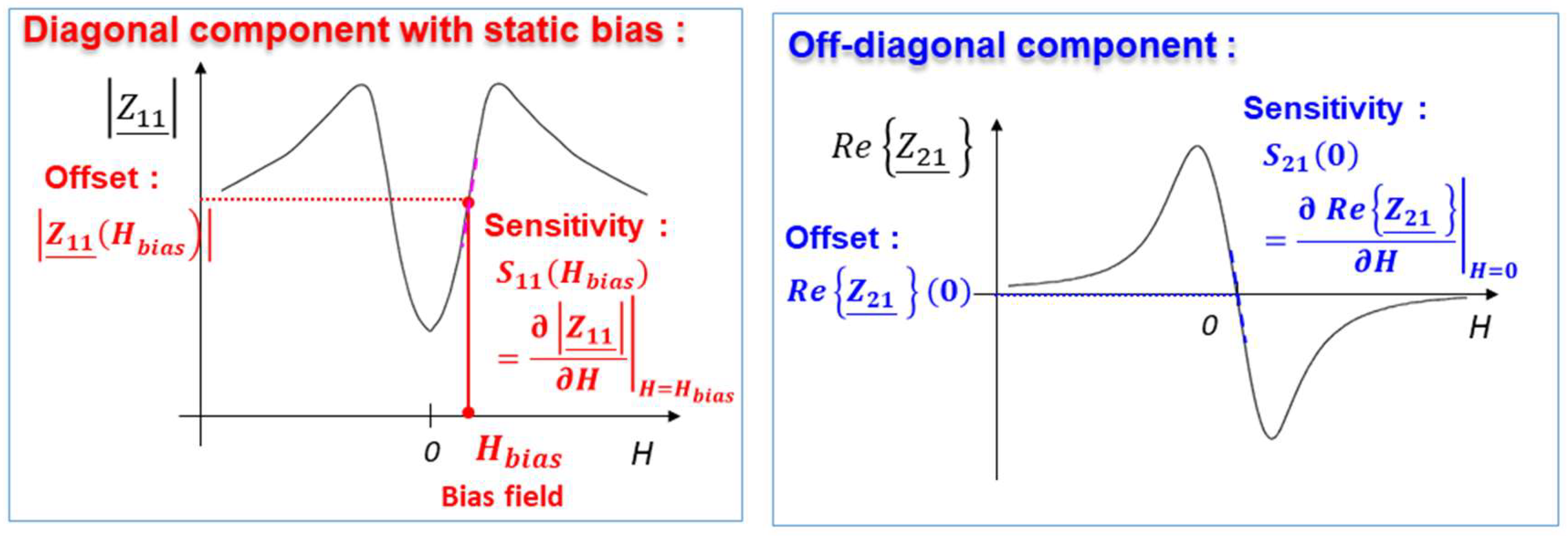
2. Quantities Considered and Experimental Setup
3. Results and Discussion
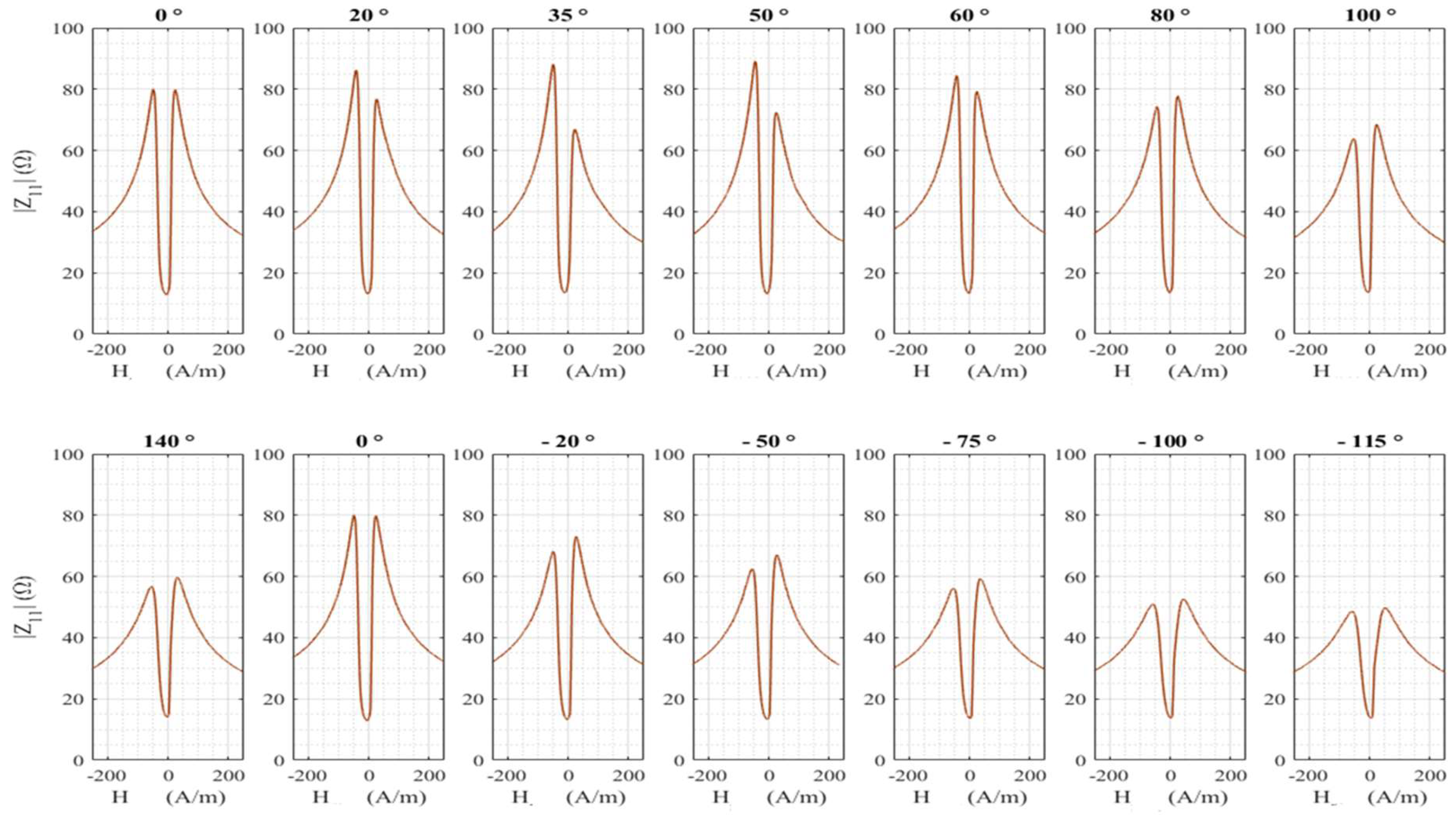
3.1. The GMI Ratio of the Diagonal Component
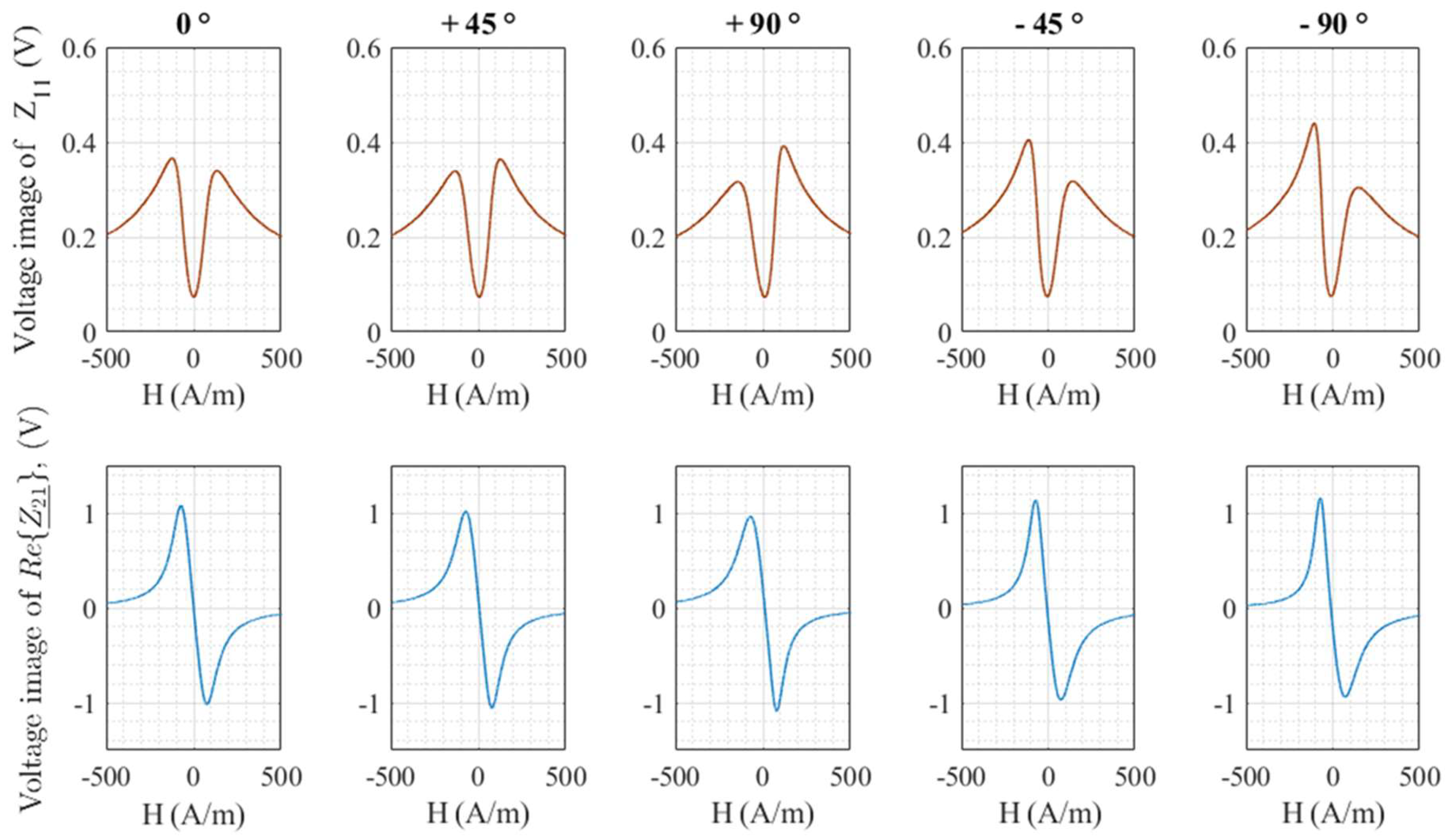
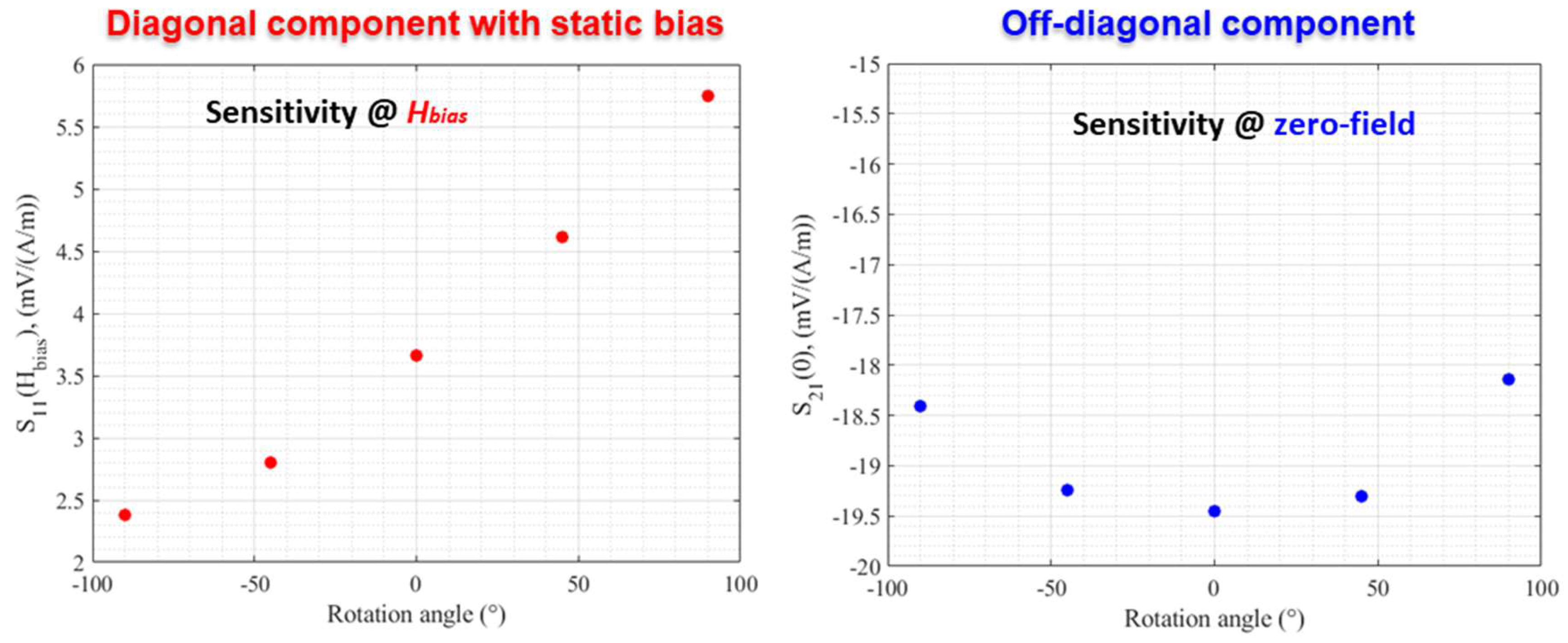
3.2. Offset and Sensitivity of the Diagonal and Off-Diagonal Components
Author Contributions
Funding
Conflicts of Interest
References
- Panina, L.V.; Mohri, K. Magneto-impedance effect in amorphous wires. Appl. Phys. Lett. 1994, 65, 1189–1191. [Google Scholar] [CrossRef]
- MI Sensor Electro-Magnetic Product Aichi Steel. Available online: https://www.aichisteel.co.jp/ENGLISH/products/electromagnetic/mi_censor/index.html (accessed on 15 July 2018).
- Coillot, C.; Moutoussamy, J.; Chanteur, G.; Robert, P.; Alves, F. On-board hybrid magnetometer of NASA CHARM-II rocket: Principle, design and performances. J. Sens. Sens. Syst. 2013, 2, 137–145. [Google Scholar] [CrossRef]
- Mohri, K.; Uchiyama, T.; Shen, L.P.; Cai, C.M.; Panina, L.V. Amorphous wire and CMOS IC-based sensitive micro-magnetic sensors (MI sensor and SI sensor) for intelligent measurements and controls. J. Magn. Magn. Mater. 2002, 249, 351–356. [Google Scholar] [CrossRef]
- Honkura, Y. Development of amorphous wire type MI sensors for automobile use. J. Magn. Magn. Mater. 2002, 249, 375–381. [Google Scholar] [CrossRef]
- Gudoshnikov, S.; Usov, N.; Nozdrin, A.; Ipatov, M.; Zhukov, A.; Zhukova, V. Highly sensitive magnetometer based on the off-diagonal GMI effect in Co-rich glass-coated microwire. Phys. Stat. Sol. 2014, 211, 980–985. [Google Scholar] [CrossRef]
- Uchiyama, T.; Mohri, K.; Nakayama, S. Measurement of Spontaneous Oscillatory Magnetic Field of Guinea-Pig Smooth Muscle Preparation Using Pico-Tesla Resolution Amorphous Wire Magneto-Impedance Sensor. IEEE Trans. Magn. 2011, 47, 3070–3073. [Google Scholar] [CrossRef]
- García, C.; Zhukov, A.; Blanco, J.M.; Zhukova, V.; Ipatov, M.; Gonzalez, J. Effect of tensile stresses on GMI of Co-rich amorphous microwires. In Proceedings of the INTERMAG Asia 2005, Digests of the IEEE International Magnetics Conference, Nagoya, Japan, 4–8 April 2005; pp. 1273–1274. [Google Scholar]
- Ciureanu, P.; Khalil, I.; Melo, L.G.C.; Rudkowski, P.; Yelon, A. Stress-induced asymmetric magneto-impedance in melt-extracted Co-rich amorphous wires. J. Magn. Magn. Mater. 2002, 249, 305–309. [Google Scholar] [CrossRef]
- Knobel, M.; Sanchez, M.L.; Velazquez, J.; Vázquez, M. Stress dependence of the giant magneto-impedance effect in amorphous wires. J. Phys. Condens. Matter 1995, 7, L115. [Google Scholar] [CrossRef]
- Knobel, M.; Pirota, K.R. Giant magnetoimpedance: Concepts and recent progress. J. Magn. Magn. Mater. 2002, 242, 33–40. [Google Scholar] [CrossRef]
- Atkinson, D.; Squire, P.T. Experimental and phenomenological investigation of the effect of stress on magneto-impedance in amorphous alloys. IEEE Trans. Magn. 1997, 33, 3364–3366. [Google Scholar] [CrossRef]
- Knobel, M.; Vazquez, M.; Hernando, A.; Sánchez, M.L. Effect of tensile stress on the field response of impedance in low magnetostriction amorphous wires. J. Magn. Magn. Mater. 1997, 169, 89–97. [Google Scholar]
- Mandal, K.; Puerta, S.; Vazquez, M.; Hernando, A. The frequency and stress dependence of giant magnetoimpedance in amorphous microwires. IEEE Trans. Magn. 2000, 36, 3257–3259. [Google Scholar] [CrossRef]
- Kim, C.G.; Yoon, S.S.; Vazquez, M. Evaluation of helical magnetoelastic anisotropy in Fe-based amorphous wire from the decomposed susceptibility spectra. J. Magn. Magn. Mater. 2001, 223, 199–202. [Google Scholar] [CrossRef]
- Blanco, J.M.; Zhukov, A.; Gonzalez, J. Effect of tensile and torsion on GMI in amorphous wire. J. Magn. Magn. Mater. 1999, 196, 377–379. [Google Scholar] [CrossRef]
- Nabias, J.; Asfour, A.; Yonnet, J.P. Investigation of Bending Stress Effect on the Diagonal and Off-Diagonal Impedances for GMI Sensor Implementation. IEEE Trans. Magn. 2017, 53, 1–8. [Google Scholar] [CrossRef]
- Nabias, J.; Asfour, A.; Yonnet, J.P. The Impact of the Bending Stress on the Performance of Giant Magneto-Impedance (GMI) Magnetic Sensors. Sensors 2017, 17, 640. [Google Scholar] [CrossRef] [PubMed]
- Beato-López, J.J.; Vargas-Silva, G.; Pérez-Landazábal, J.I.; Gómez-Polo, C. Giant Stress-Impedance (GSI) sensor for diameter evaluation in cylindrical elements. Sens. Actuators A Phys. 2018, 269, 269–275. [Google Scholar] [CrossRef]
- Chizhik, A.; Gonzalez, J.; Zhukov, A.; Stupakiewcz, A. Torsion stress induced magnetic switching in amorphous microwires. IEEE Magn. Lett. 2017, 8, 1–5. [Google Scholar] [CrossRef]
- Blanco, J.M.; Zhukov, A.; Gonzalez, J. Torsional Stress Impedance and Magneto-impedance in (Co0.95Fe0.05)72.5Si12.5B15 Amorphous Wire with Helical Induced Anisotropy. J. Phys. D Appl. Phys. 1999, 32, 3140–3145. [Google Scholar] [CrossRef]
- Tejedor, M.; Hernando, B.; Sanchez, M.L.; Prida, V.M.; Vazquez, M. The torsional dependence of the magneto-impedance effect in current-annealed Co-rich amorphous wires. J. Phys. D Appl. Phys. 1998, 31, 3331–3336. [Google Scholar] [CrossRef]
- Blanco, J.M.; Zhukov, A.; Gonzalez, J. Asymmetric torsion stress giant magnetoimpedance in nearly-zero magnetostrictive amorphous wires. J. Appl. Phys. 2000, 87, 4813–4815. [Google Scholar] [CrossRef]
- Blanco, J.M.; Zhukov, A.; Chen, A.P.; Cobeño, A.F.; Chizhik, A.; Gonzalez, J. Asymmetric torsion giant impedance in nearly-zero magnetostrictive amorphous wires with induced helical anisotropy. J. Phys. D Appl. Phys. 2001, 34, L31–L34. [Google Scholar] [CrossRef]
- García, K.L.; García-Beneytez, J.M.; Valenzuela, R.; Zhukov, A.; González, J.; Vázquez, M. Effects of Torsion on the Magnetoimpedance Response of CoFeBSi Amorphous Wires. J. Magn. Magn. Mater. 2001, 226, 731–733. [Google Scholar]
- Antonov, A.S.; Buznikov, N.A.; Granovsky, A.B. Asymmetric Giant Magnetoimpedance of Amorphous Microwires under the Action of Torsional Stresses. Tech. Phys. Lett. 2014, 40, 267–270. [Google Scholar] [CrossRef]
- Ménard, D.; Seddaoui, D.; Melo, L.G.C.; Yelon, A.; Dufay, B.; Saez, S.; Dolabdjian, C. Perspectives in giant magnetoimpedance magnetometry. Sens. Lett. 2009, 73, 339–342. [Google Scholar] [CrossRef]
- Ipatov, M.; Zhukova, V.; Zhukov, A.; Gonzalez, J. Magnetoimpedance sensitive to dc bias current in amorphous microwires. Appl. Phys. Lett. 2010, 97, 252507. [Google Scholar] [CrossRef]
- Ipatov, M.; Chizhik, A.; Zhukova, V.; Gonzalez, J.; Zhukov, A. Correlation of surface domain structure and magneto-impedance in amorphous microwires. J. Appl. Phys 2011, 109, 113924. [Google Scholar] [CrossRef]
- Buznikov, N.A.; Antonov, A.S.; Granovsky, A.B. Asymmetric magnetoimpedance in amorphous microwires due to bias current: Effect of torsional stress. J. Magn. Magn. Mater. 2014, 355, 289–294. [Google Scholar] [CrossRef]
- Sandacci, D.; Makhnovskiy, D.; Panina, L.; Mohri, K.; Honkura, Y. Off-diagonal impedance in amorphous wires and its application to linear magnetic sensors. IEEE Trans. Magn. 2004, 40, 3505–3511. [Google Scholar] [CrossRef] [Green Version]
- Makhnovskiy, D.P.; Panina, L.V.; Mapps, D.J. Measurement of field-dependent surface impedance tensor in amorphous wires with circumferential anisotropy. J. Appl. Phys. 2000, 87, 4804–4805. [Google Scholar] [CrossRef]
- Antonov, A.S.; Iakubov, I.T.; Lagarkov, A.N. Nondiagonal impedance of amorphous wires with circular magnetic anisotropy. J. Magn. Magn. Mater. 1998, 187, 252–260. [Google Scholar] [CrossRef]
- Zhukov, M.; Ipatov, M.; Zhukova, V.; García, C.; Gonzalez, J.; Blanco, J.M. Development of ultra-thin glass-coated amorphous microwires for HF magnetic sensor applications. Phys. Status Solidi 2008, 205, 1367–1372. [Google Scholar] [CrossRef]
- Asfour, A.; Yonnet, J.P.; Zidi, M. A high dynamic range GMI current sensor. J. Sens. Technol. 2012, 2, 165. [Google Scholar] [CrossRef]
- Kabanov, Y.; Zhukov, A.; Zhukova, V.; Gonzalez, J. Magnetic domain structure of wires studied by using the magneto-optical indicator film method. Appl. Phys. Lett. 2005, 87, 142507. [Google Scholar] [CrossRef]
- Mohri, K.; Humphrey, F.R.; Kawashimay, K.; Kimura, K.; Mizutani, M. Large Barkhausen and Matteucci effects in FeCoSiB, FeCrSiB, and FeNiSiB. IEEE Trans. Magn. 1990, 26, 1789. [Google Scholar] [CrossRef]
- Zhukova, V.; Blanco, J.M.; Ipatov, M.; Zhukov, A. Effect of transverse magnetic field on domain wall propagation in magnetically bistable glass-coated amorphous microwires. J. Appl. Phys 2009, 106, 113914. [Google Scholar] [CrossRef]
- Zhukova, V.; Usov, N.A.; Zhukov, A.; Gonzalez, J. Length effect in Co-rich amorphous wire. Phys. Rev. B 2002, 65, 134407. [Google Scholar] [CrossRef]
- Phan, M.; Peng, H. Giant magnetoimpedance materials: Fundamentals and applications. Prog. Mater. Sci. 2008, 53, 323–420. [Google Scholar] [CrossRef]
- Dufay, B.; Saez, S.; Dolabdjian, C.P.; Yelon, A.; Menard, D. Characterization of an optimized off-diagonal GMI-based magnetometer. IEEE Sens. J. 2013, 13, 379–388. [Google Scholar] [CrossRef]
- Seddaoui, D.; Ménard, D.; Movaghar, B.; Yelon, A. Nonlinear electromagnetic response of ferromagnetic metals: Magnetoimpedance in microwires. J. Appl. Phys. 2009, 105, 083916. [Google Scholar] [CrossRef]
- Paperno, E. Suppression of magnetic noise in the fundamental-mode orthogonal fluxgate. Sens. Actuators A 2004, 116, 405–409. [Google Scholar] [CrossRef] [Green Version]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nabias, J.; Asfour, A.; Yonnet, J.-P. Effect of Torsion Stress on the Offset and Sensitivity of Diagonal and Off-Diagonal GMI in Amorphous Wires. Sensors 2018, 18, 4121. https://doi.org/10.3390/s18124121
Nabias J, Asfour A, Yonnet J-P. Effect of Torsion Stress on the Offset and Sensitivity of Diagonal and Off-Diagonal GMI in Amorphous Wires. Sensors. 2018; 18(12):4121. https://doi.org/10.3390/s18124121
Chicago/Turabian StyleNabias, Julie, Aktham Asfour, and Jean-Paul Yonnet. 2018. "Effect of Torsion Stress on the Offset and Sensitivity of Diagonal and Off-Diagonal GMI in Amorphous Wires" Sensors 18, no. 12: 4121. https://doi.org/10.3390/s18124121
APA StyleNabias, J., Asfour, A., & Yonnet, J.-P. (2018). Effect of Torsion Stress on the Offset and Sensitivity of Diagonal and Off-Diagonal GMI in Amorphous Wires. Sensors, 18(12), 4121. https://doi.org/10.3390/s18124121





