4.1. Preliminaries
Petri net is a well-known mathematical modeling technique that portrays the different states of a system. It is a directed graph built of two types of nodes: places, which are depicted as circles, and transitions depicted as rectangles. Places can be connected only to transitions, and transitions only to places. Petri net has proven to be efficient and reliable for describing and analyzing the flow of complex and concurrent systems, such as healthcare. Different types of nodes are connected using directed arcs, and places contain solid bullets which denote the tokens representing the activities performed by the transitions. A transition is fired or executed after it is enabled, and then tokens are removed from every input place of the fired transition and generated into each output place connected to that transition. Petri net has numerous features, including reachability and soundness.
Reachability in this context is the ability to reach a certain node from another, and soundness is the ability to produce an output when given an input. Soundness is a very important Petri net feature because, if the net is sound, the topology of the workflow is correct. A general Petri net model is illustrated in
Figure 4. The Petri net graph allows a model representation by using nodes that either represent transitions (added as rectangles) or places (added as circles). One transition can be connected to one or more places and vice versa, one place can be connected to one or more transitions. In case of identical types, the nodes will not be directly connected. Directed arcs are used to connect different types of nodes. Activities that are performed by the transitions are represented by tokens (solid circles) which reside in places. If a place (P) connected to a transition (T) is empty, the transition will not be executed. Therefore, an enabled transition exists if and only if no empty places are connected to this transition as input. The execution of a transition happens after it is enabled; we say the transition is fired. As a result of this firing, new tokens are created in each of the output places after removal of all tokens from each of the input places. The weights of arcs connecting the fired transition with its input and output places affect the number of tokens to be added or removed.
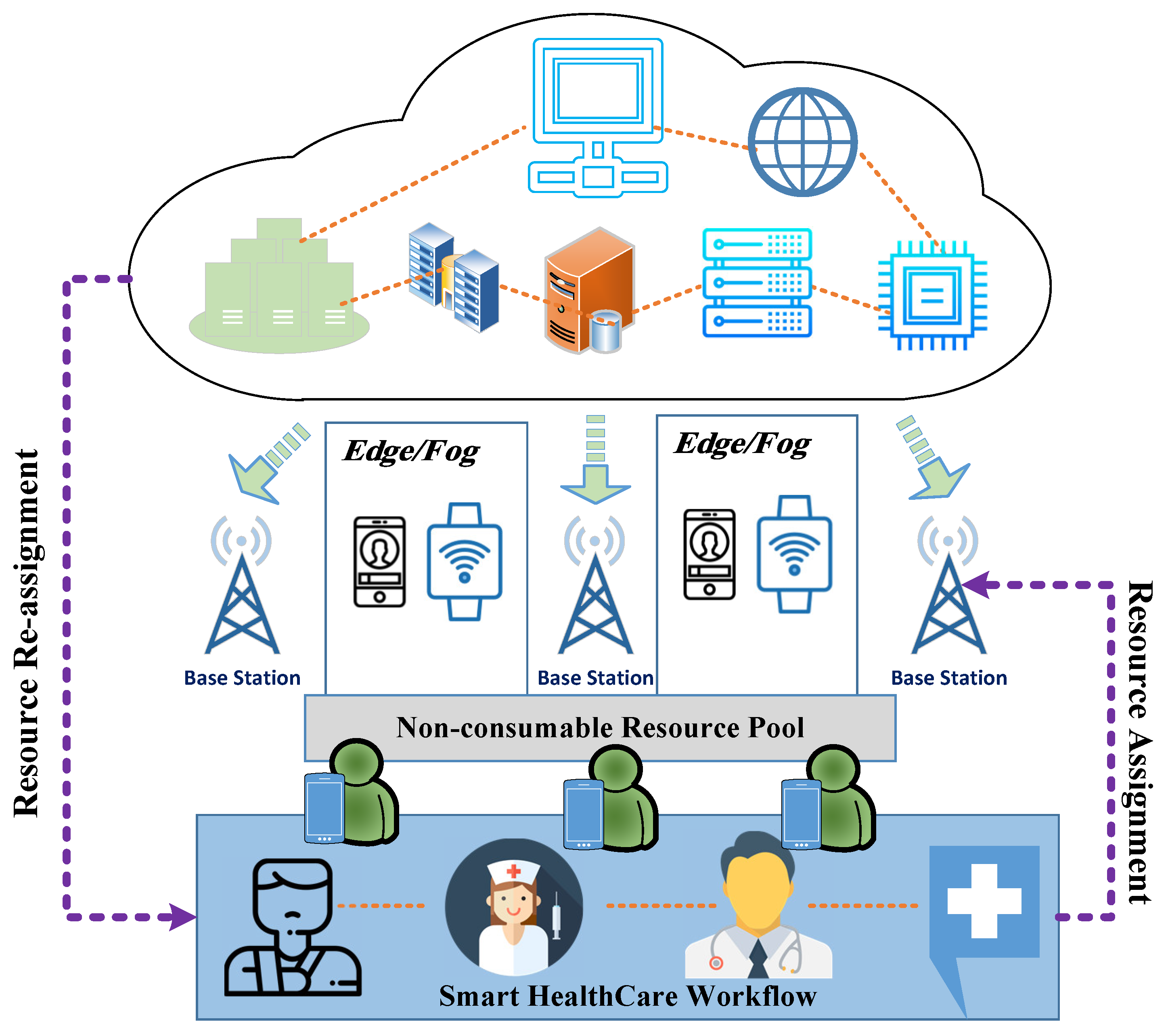
Many extensions and subclasses have been introduced in literature to solve concurrency problems. With Petri nets and workflows, tasks are modeled by transitions and dependencies by places and arcs [
44]. When using Petri nets to model complex industrial workflows, systems are guaranteed to behave the way they are intended by two main Petri net characteristics: safety and soundness. Due to the complexity of healthcare systems and the many input factors, the systems can be seen as pipelines with stages that are considered critical sections; that is, the stages can serve only one patient at a time. Non-consumable resources are in pools, and, if they leave their pool to be involved in a task they need to return back to that pool after the task is completed, so they can be reassigned to another task. These critical sections must be handled with care, in order to maintain the soundness of the workflow system [
45]. The importance of Petri net models as a detailed approach for formulating dynamic processes is presented by Huang et al. [
46].
A Petri net ℵ is mathematically described as follows:
where
is a non-empty set of places,
is a non-empty set of transitions,
is a non-empty set that represents the topology of the net, a set of arcs that joins places and transitions, and
which is the set of weights of those arcs. The set of arcs
is mathematically described as follows:
From Equation (
2), it is obvious that places can only be connected to transitions and transitions can only be connected to places. No direct connection can exist between two places or two transitions. Every connection
or
has a weight which is an integer with a minimum value of one. This integer specifies the minimum number of activities required to flow at anytime through the arc.
Reachability is an important feature of Petri nets—that is, which node in the graph is reachable from which node.
Figure 4 shows a Petrinet with full reachability because of the feedback between
and
through
. In this graph, we can say that
is reachable from
since there is a path that leads from
to
. This is mathematically written as follows:
Tokens move inside Petri nets. They reside in places until being consumed by transitions during the firing process and then reproduced in other places according to the topology of the net. In
Figure 4,
has 1 token and
has 1 token. This means that transitions
and
are enabled and
and
are disabled since the inputs of
and
have tokens and the inputs of
and
do not. Since
and
are enabled, they can fire and when they do, tokens are consumed from
and
(leaving them as empty places) and reproduced in
ands
. Now, the only transition that is enabled is
since all its inputs have tokens. When it fires, tokens are consumed from
and
and one token is reproduced in
, which, in turn, enables
. When
fires, it consumes the token in
and produces two tokens in
and
.
The dynamic behavior of Petri nets is described by marking. Marking is the distribution of tokens in the Petri net. It is represented as a vector with a length of . In other words, the length of the marking vector is as long as set , where every place has a marking. The initial marking of the net is denoted and at time t to be . The marking of place j at time t is denoted as .
The set of input places to a transition
is denoted as
and the set of output places from a transition
is denoted
. The same goes for places. The set of input transitions to place
is denoted as
and the set of output transitions from place
is denoted as
. In
Figure 4,
and
. Workflow nets are Petri nets with a single input place
i and a single output place
o.
The proposed Petri net model, RPN, is a workflow net that is validated using discrete mathematics. The validation is performed through proposing a Theorem of soundness. Mathematically, soundness is defined as follows:
In other words, any input marking will eventually reach the output of the net.
4.2. System Validation
An RPN
is a tuple that is defined as:
and
where
is the set of pools of preserved resources, a set of controlled siphons.
is the set of places where
.
is the set of transitions.
is the set of resources, and
is the mapping function that assigns resources to pools.
A transition can be fired only if the required number of tokens at the input place is met. Different types of resources are defined in the system, each responsible for a certain task in order to accomplish the activity. We define the validity of a workflow to be the property of which the workflow behaves the way it is designed to behave. With this definition, we propose the following Theorem:
Theorem 1. | A workflow is valid if | 1- | ℵ is a sound workflow net. |
| 2- | and |
| 3- | Ifandthen |
| 4- | . |
| 5- | , ifthen |
| 6- | . |
Condition (1) of the Theorem states that the original workflow ℵ before applying the pools has to be sound. Condition (2) states that, for all the resources in the system, they have to exist in their pools at time 0 and after the process finishes execution (). Condition (3) states that, if there is a place P and a pool that are inputs to transition T and P is marked, then is guaranteed to be eventually marked. Condition (4) discusses the topological correctness of the workflow. It says that every pool has to be an input to a transition and an output from a transition . Condition (5) guarantees that siphons will never affect the soundness of the original workflow ℵ. It states that, if there is a transition with an input pool, then the output is reachable from T. Condition (6) guarantees that no tokens are consumed inside any transition so the number of tokens used to enable a transition is the number of token that will be reproduced after it fires. We prove the Theorem as follows:
Proof of Theorem 1. | ∵ | ℵ is sound | |
| ∴ | | (1) |
| ∵ | | |
| ∵ | and | |
| ∵ | . | |
| ∵ | , if then | |
| ∴ | is a sound workflow | (2) □ |
| ∵ | | |
| ∴ | is sound | (3) |
| ∴ | | (4) |
| ∴ | | (5) |
| From | (2), (3), (4) and (5) | |
| | is a valid RPN. | |
Theorem 1 defines the conditions that have to be applied for a workflow to be a valid RPN. Out of this theorem, we propose the following theorem:
Theorem 2. An RPN is sound if and only if is valid.
To prove this theorem, we need to prove that if is valid then it is sound and if is sound then it is valid. To prove that if it is sound then it is valid is already done as a result of Theorem 1. The following is the proof that, if is valid, then it is sound:
Proof of Theorem 2. | ∵ | is valid | |
| ∴ | and | |
| ∴ | are well controlled siphons. | |
| ∵ | , if then | □ |
| ∴ | | |
| ∴ | | |
| ∴ | is sound. | |