Crack Assessment of Wheel Hubs via an Ultrasonic Transducer and Industrial Robot
Abstract
:1. Introduction
2. Experimental Method and Configuration
2.1. Analysis of Cracks in Wheel Hubs
- Heat damage. Friction-heat is generated within bearings during high-speed operation and is then transmitted to the hub. The area most affected is the interface between the hub and the outer bearing ring. There are two causes of heat cracking: a quenching effect caused by the rapid cooling of a hot surface, and thermal stress caused by the uneven heating of a local surface.
- Fatigue damage. Micro-cracks appear in wheel hubs under long-term cyclic loads, but do not affect normal operation until they become enlarged. Fatigue cracks are generally sub-surface in location and extend both inwards and outwards, finally causing accidents. Crack growth is remarkably random in nature, rendering crack detection difficult. Complete scans are ideally required.
- Impact damage. Although wheel hubs feature many micro-cracks, these do not expand rapidly. However, the impact load accelerates crack growth, rapidly reducing effectiveness. As impact loads will greatly reduce service life, such loads should be avoided.
2.2. Crack Test Methodology
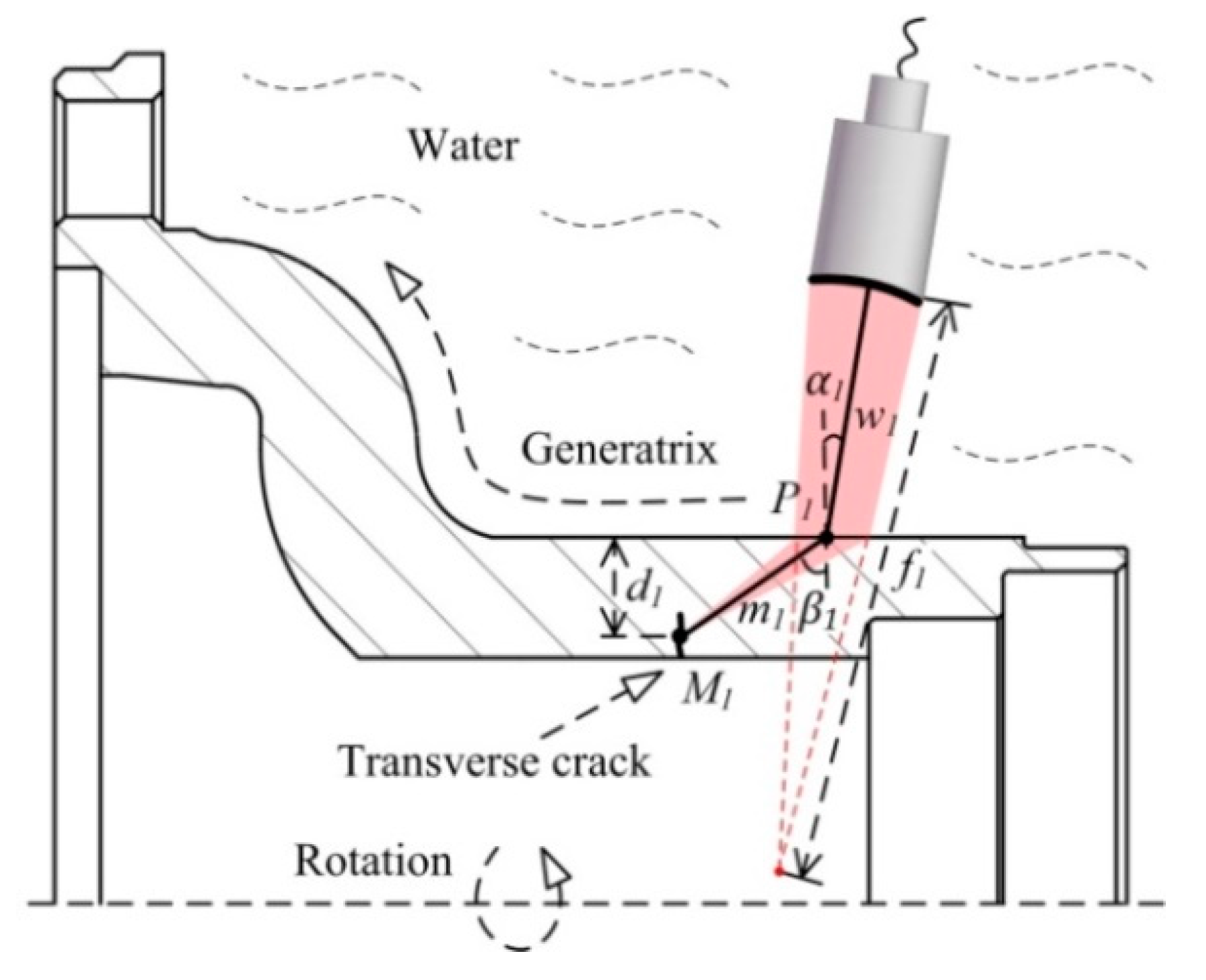
2.2.1. Transverse Crack Test
2.2.2. Longitudinal Crack Test
2.3. Configuration of the Test System
2.3.1. Mechanism
2.3.2. Ultrasonic Testing
2.3.3. Motion Control
3. Experiment Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- John, C. Castings Practice; Butterworth-Heinemann: Oxford, UK, 2004; ISBN 9780750647915. [Google Scholar]
- Hübner, P.; Schlosser, H.; Pusch, G.; Biermann, H. Load history effects in ductile cast iron for wind turbine components. Int. J. Fatigue 2007, 29, 1788–1796. [Google Scholar] [CrossRef]
- Principe, R.; Vallejo, L.M.; Bailey, J.; Berthet, R.; Favier, L.; Grand-Clement, L.; Savary, F. Phased Array Ultrasonic Nondestructive Tests of Soldered Current-Carrying Bus-Bar Splices of Superconducting Magnets. IEEE Trans. Appl. Supercond. 2018, 28, 1–8. [Google Scholar] [CrossRef]
- Charles, J.H. Handbook of Nondestructive Evaluation; McGraw-Hill: New York, NY, USA, 2003; ISBN 9780070281219. [Google Scholar]
- Collins, D.N.; Alcheikh, W. Ultrasonic non-destructive evaluation of the matrix structure and the graphite shape in cast iron. J. Mater. Process. Technol. 1995, 55, 85–90. [Google Scholar] [CrossRef]
- Shi, D.; Kang, K.; Gao, G.; Miao, S. System and Experiment on Fast Testing Vermicular Graphite Percent in Cast Iron Based on Ultrasonic Longitudinal Wave. Mater. Trans. 2016, 57, 544–548. [Google Scholar] [CrossRef] [Green Version]
- Kachanov, V.K.; Sokolov, I.V.; Rodin, A.B.; Voronkova, L.V. Ultrasonic testing of complexly structured cast-iron articles using a multifunctional software-hardware measuring system. Russ. J. Nondestruct. Test. 2008, 44, 733–746. [Google Scholar] [CrossRef]
- Ma, H.W.; Zhang, X.H.; Wei, J. Research on an ultrasonic NDT system for complex surface parts. J. Mater. Process. Technol. 2002, 129, 667–670. [Google Scholar] [CrossRef]
- Summan, R.; Pierce, S.; Dobie, G.; Hensman, J.; MacLeod, C. Practical constraints on real time Bayesian filtering for NDE applications. Mech. Syst. Signal Process. 2014, 42, 181–193. [Google Scholar] [CrossRef] [Green Version]
- Mineo, C.; Pierce, S.G.; Nicholson, P.I.; Cooper, I. Robotic path planning for non-destructive testing—A custom MATLAB toolbox approach. Robot. Comput. Integr. Manuf. 2016, 37, 1–12. [Google Scholar] [CrossRef]
- Mineo, C.; Summan, R.; Riise, J.; Macleod, C.N.; Pierce, S.G. Introducing a New Method for Efficient Visualization of Complex Shape 3D Ultrasonic Phased-Array C-Scans. In Proceedings of the IEEE International Ultrasonics Symposium, Washington, DC, USA, 6–9 September 2016. [Google Scholar]
- Mineo, C.; MacLeod, C.; Morozov, M.; Pierce, S.G.; Summan, R.; Rodden, T.; Kahani, D.; Powell, J.; McCubbin, P.; McCubbin, C.; et al. Flexible Integration of Robotics, Ultrasonics and Metrology for the Inspection of Aerospace Components. In Proceedings of the 43rd Review in Quantitative Nondestructive Evaluation, Atlanta, GA, USA, 17–22 July 2016. [Google Scholar]
- Irwin, G.R. Analysis of Stresses and Strains Near the End of a Crack Traversing a Plate. J. Appl. Mech. 1957, 24, 361–364. [Google Scholar]
- British Standards Institution. British Standard (BS) 7448–4:1997, Fracture Mechanics Toughness Tests—Part 4: Method for Determination of Fracture Resistance Curves and Initiation Values for Stable Crack Extension in Metallic Materials; British Standards Institution: London, UK, 1997; ISBN 0580286304. [Google Scholar]
- British Standards Institution. British Standard (BS) 7910:2013, Guide to Methods for Assessing the Acceptability of Flaws in Metallic Structures; British Standards Institution: London, UK, 2013; ISBN 9780580951985. [Google Scholar]
- Xiao, Z.; You, Y.; Xu, C.G.; Xiao, D.G. Profile tracking with ultrasonic alignment for automatic non-destructive testing of complex structures. Robot. Comput. Integr. Manuf. 2018, 49, 134–142. [Google Scholar]
- John, J.C. Introduction to Robotics: Mechanics and Control, 3rd ed.; Addison-Wesley: Boston, MA, USA, 1989; ISBN 9780201543612. [Google Scholar]










| Apparatus | Brand | Model | Property |
|---|---|---|---|
| Robot | Staubli (Pfäffikon, Switzerland) | TX90XL-HE | Repeatability 0.035 mm |
| Motor of the turntable | Parker (Cleveland, OH, USA) | SME Series | Power 1.57 kW, Torque 6 Nm |
| Motor controller | Parker (Cleveland, OH, USA) | Complex 3 Series | Control via CAN Open |
| Ultrasonic pulser/reciver | Olympus (Tokyo, Japan) | 5077PR | Receiving bandwidth 1 kHz–35 MHz |
| Ultrasonic transducer | Olympus (Tokyo, Japan) | V319-SU-F4.0IN | Centre frequency 15 MHz |
| A/D converter | Acquisition Logic (Chantilly, VA, USA) | AL12200 | Sampling rate 100 MHz |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Xu, C.; Xiao, D. Crack Assessment of Wheel Hubs via an Ultrasonic Transducer and Industrial Robot. Sensors 2018, 18, 4336. https://doi.org/10.3390/s18124336
Zhang H, Xu C, Xiao D. Crack Assessment of Wheel Hubs via an Ultrasonic Transducer and Industrial Robot. Sensors. 2018; 18(12):4336. https://doi.org/10.3390/s18124336
Chicago/Turabian StyleZhang, Hanming, Chunguang Xu, and Dingguo Xiao. 2018. "Crack Assessment of Wheel Hubs via an Ultrasonic Transducer and Industrial Robot" Sensors 18, no. 12: 4336. https://doi.org/10.3390/s18124336
APA StyleZhang, H., Xu, C., & Xiao, D. (2018). Crack Assessment of Wheel Hubs via an Ultrasonic Transducer and Industrial Robot. Sensors, 18(12), 4336. https://doi.org/10.3390/s18124336




