A Novel Vision-Based Pose Measurement Method Considering the Refraction of Light
Abstract
:1. Introduction
2. Photography Model under Wind Tunnel Environment
3. Calibration Method
3.1. Calibration Method for the Normal Vector of the Observation Window
3.2. Calculation Method for the External Parameters of the Camera
4. High Signal-to-Noise Ratio Image Acquisition of the Falling Target
5. Image Processing
6. Experiment and Results
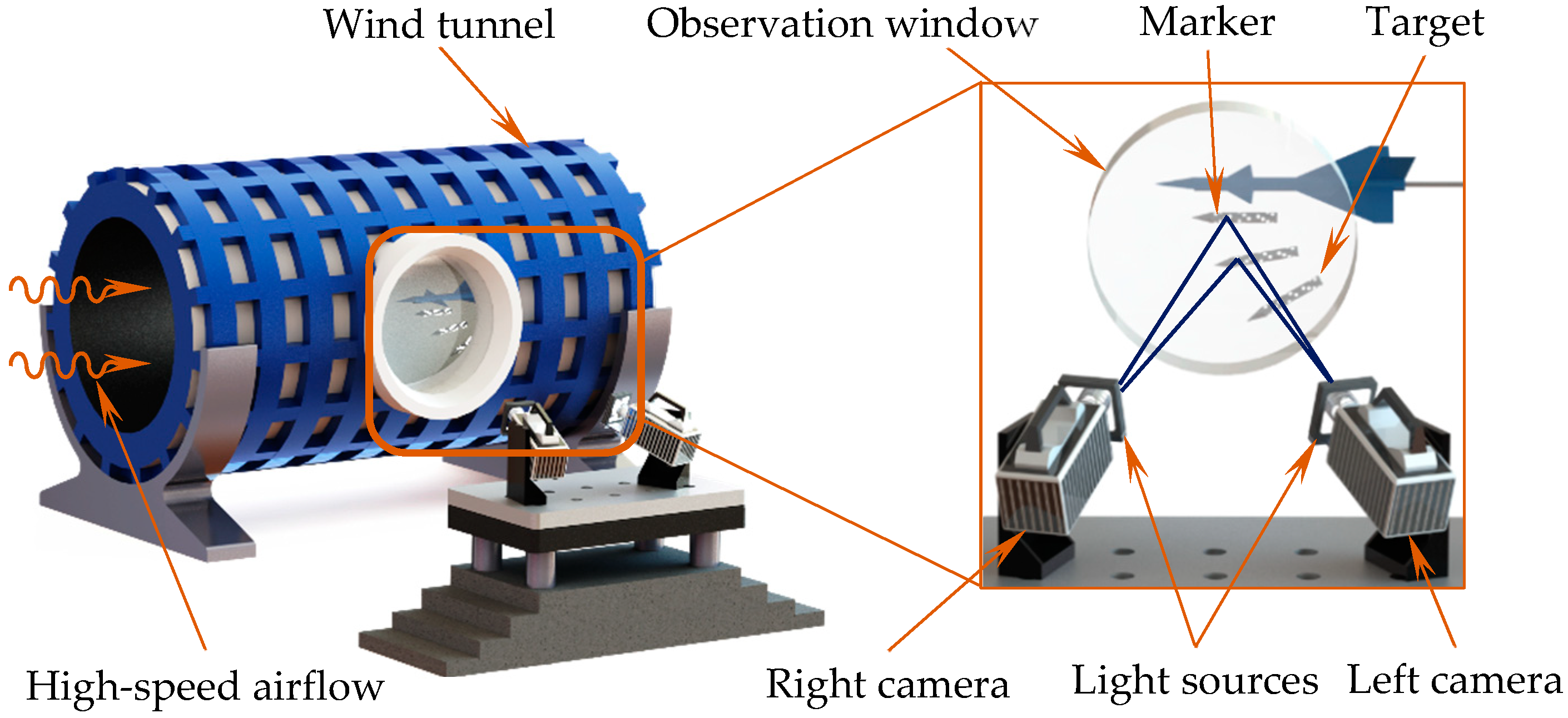
6.1. Vision-Based Measurement System
6.2. Accuracy Validation Experiments
6.3. Vision Measurement Experiment
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lee, J.J.; Ho, H.N.; Lee, J.H. A Vision-based dynamic rotational angle measurement system for large civil structures. Sensors 2012, 12, 7326–7336. [Google Scholar] [CrossRef]
- Liu, W.; Shang, Z.; Ma, X.; Zhang, Y.; Li, X.; Jia, Z. Position and attitude measuring method of auxiliary tank based on color-coding method in wind tunnel environment. Acta Aeronaut. Astronaut. Sin. 2014, 36, 1556–1563. [Google Scholar]
- Ma, X.; Liu, W.; Chen, L.; Li, X.; Jia, Z.; Shang, Z. Simulative technology for auxiliary fuel tank separation in a wind tunnel. Chin. J. Aeronaut. 2015, 29, 608–616. [Google Scholar] [CrossRef]
- Graves, S.S.; Burner, A.W. Development of an intelligent videogrammetric wind tunnel measurement system. In Proceedings of the Conference on Optical Diagnostics for Fluids, Solids, and Combustion, San Diego, CA, USA, 31 July–2 August 2001. [Google Scholar]
- Murray, N.E.; Bernard, J.J.; Gui, L.; Seiner, J.M. Measurements of store separation dynamics. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Martinez, B.; Bastide, M.; Wey, P. Free flight measurement technique in shock tunnel. In Proceedings of the 30th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Maletsky, L.P.; Sun, J.; Morton, N.A. Accuracy of an optical active-marker system to track the relative motion of rigid bodies. J. Biomech. 2007, 40, 682–685. [Google Scholar] [CrossRef]
- Jones, T.; Lunsford, C. Design and development of a real-time model attitude measurement system for hypersonic facilities. In Proceedings of the 43th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- Burner, A.W.; Liu, T. Videogrammetric model deformation measurement technique. J. Aircr. 2001, 38, 745–754. [Google Scholar] [CrossRef]
- Sant, Y.L.; Mignosi, A.; Deléglise, B.; Bourguignon, G. Model Deformation Measurement (MDM) at Onera. In Proceedings of the 25th AIAA Applied Aerodynamics Conference, Miami, FL, USA, 25–28 June 2007. [Google Scholar]
- Jia, Z.; Ma, X.; Liu, W.; Lu, W.; Li, X.; Chen, L.; Wang, Z.; Cui, X. Pose Measurement method and experiments for high-speed rolling targets in a wind tunnel. Sensors 2014, 14, 23933–23953. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Ma, X.; Chen, L.; Jia, Z.; Liu, W.; Li, X.; Zhang, J.; Lu, J. Remote-controlled flexible pose measurement system and method for a moving target in wind tunnel. Chin. J. Aeronaut. 2018, 31, 89–98. [Google Scholar] [CrossRef]
- Tsai, R.Y. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses. IEEE J. Robot. Autom. 1987, 3, 323–344. [Google Scholar] [CrossRef]
- Agrawal, A.; Ramalingam, S.; Taguchi, Y.; Chari, V. A theory of multi-layer flat refractive geometry. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Zhang, Z.Y. Camera calibration with one-dimensional objects. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 892–899. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, X.; Yang, Y.H. Two-view camera housing parameters calibration for multi-layer flat refractive interface. In Proceedings of the 27th IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Liu, W.; Liu, S.; Zhang, Y.; Shang, Z.; Ma, X. An image acquiring method for position and attitude measurement of high-speed target in wind tunnel. Sens. Transducers 2013, 160, 635–644. [Google Scholar]
- McKenna, S.J.; Jabri, S.; Duric, Z.; Rosenfeld, A.; Wechsler, H. Tracking groups of people. Comput. Vis. Image Underst. 2000, 80, 42–56. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, Z.; Wang, Z.; Wang, Y.; Zhou, W. The trajectory prediction of spacecraft by grey method. Meas. Sci. Technol. 2016, 27, 35–45. [Google Scholar] [CrossRef]
- Barron, J.L.; Fleet, D.J.; Beauchemin, S.S. Performance of optical flow techniques. Int. J. Comput. Vis. 1994, 12, 43–77. [Google Scholar] [CrossRef] [Green Version]
- Yao, J. Image registration based on both feature and intensity matching. In Proceedings of the 2001 IEEE International Conference on Acoustics, Speech and Signal Processing, Salt Lake City, UT, USA, 7–11 May 2001. [Google Scholar]
- Pluim, J.P.W.; Maintz, J.B.A.; Viergever, M.A. Mutual information matching in multiresolution contexts. Image Vis. Comput. 2001, 19, 45–52. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, D.; Peng, Z.; Zhang, J. Improved iterative pose estimation algorithm using three-dimensional feature points. Opt. Eng. 2007, 46, 1–8. [Google Scholar] [CrossRef]
















© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Ma, X.; Li, X.; Pan, Y.; Wang, F.; Jia, Z. A Novel Vision-Based Pose Measurement Method Considering the Refraction of Light. Sensors 2018, 18, 4348. https://doi.org/10.3390/s18124348
Liu W, Ma X, Li X, Pan Y, Wang F, Jia Z. A Novel Vision-Based Pose Measurement Method Considering the Refraction of Light. Sensors. 2018; 18(12):4348. https://doi.org/10.3390/s18124348
Chicago/Turabian StyleLiu, Wei, Xin Ma, Xiao Li, Yi Pan, Fuji Wang, and Zhenyuan Jia. 2018. "A Novel Vision-Based Pose Measurement Method Considering the Refraction of Light" Sensors 18, no. 12: 4348. https://doi.org/10.3390/s18124348
APA StyleLiu, W., Ma, X., Li, X., Pan, Y., Wang, F., & Jia, Z. (2018). A Novel Vision-Based Pose Measurement Method Considering the Refraction of Light. Sensors, 18(12), 4348. https://doi.org/10.3390/s18124348




