1. Introduction
Poor air quality has been linked to human health effects with increased associated diseases and symptoms since the rapid growth period associated with the 4th industrial revolution [
1,
2]. This is partly linked to emissions from combustion processes associated with cheap fossil fuel and coal-based energy. Several pollutants affecting air quality are of major concern in developed countries, especially in urban region, including carbon monoxide (CO), nitrogen dioxide (NO
2) and secondary pollutants such as ozone (O
3) [
3]. In Malaysia these gas pollutants are usually found at significantly high concentrations over urban areas such as the Klang Valley, as reported by Latif et al., Banan et al., Ahamad et al. and Ismail et al. [
4,
5,
6,
7]. In line with these findings, it is important for local authorities to continuously monitor these pollutants.
Typically, air quality monitoring is carried out using a reference technique or equivalent method at a fixed ground location such as chemiluminescent measurements used for NO, NO
2 monitoring and dispersive infra-red measurements for CO monitoring [
8,
9]. However, these techniques have been shown to have difficulties in terms of routine maintenance, such as calibration and quality control, in addition to requiring high-security locations to avoid theft [
9]. Therefore, there are limited numbers of reference monitoring stations that can provide data and these are generally located away from source emissions. This leads to poor spatial air quality data coverage and the impact of local sources to air quality may not be considered [
10]. Thus, alternative air pollution monitoring approaches have emerged such as low-cost air quality measurement techniques [
11].
Previous studies have applied low-cost air quality sensor (LAQS) nodes in air quality networks such as at rural and urban sites, road-side sites and also in mobile vehicular measurements [
12,
13,
14]. A large proportion of LAQSs use electrochemical (EC) sensors as detectors to measure several of the common gas pollutants. Compared to the conventional method, LAQSs have brought a new paradigm for air monitoring, making it possible to install sensors in many more locations. However, there is still an issue regarding data quality in sensor applications. Some data sensors are considerably influenced by meteorological conditions such as temperature and humidity, and even interference from other gas air pollutants [
15]. In tropical countries such as Malaysia, humidity is higher than in temperate regions and may affect the results from LAQSs. Thus, undertaking LAQS measurements is essential to investigate the performance of these sensors.
Moreover, there is a lack of an established protocol, which is proven to ensure and control the quality of data, especially while LAQSs are deployed in the field [
11]. Consequently, methods or algorithms have been developed to solve these obstacles, to observe a linear relationship between the injected known concentration and the corresponding sensor response, temperature and humidity cycle, cross sensitivity with the other gas pollutant. More sophisticated calibration techniques such as the artificial neural network (ANN) techniques are used to correct the raw data [
13,
16,
17,
18,
19].
ANN methods have previously been applied as tools for modeling nonlinear complex systems and predictions [
20]. Several studies in the area of sensor calibration have used an ANN technique. Huyberechts et al. [
21] used an ANN to process the signal arising from a three-sensor array for the identification of organic compounds such as methane (CH
4) and carbon monoxide (CO) at high concentration levels. The results showed that the calibration model which was developed using an ANN had a good quantitative result with a relative error of ≤5%. Multilayer perceptron, one type of structure of ANN, has been used as a tool to analyze data from sensor arrays for the quantification of the concentrations of six indoor air contaminants—formaldehyde, benzene, toluene, ammonia, CO and nitrogen dioxide (NO
2) [
22]. In another study, Spinele et al. [
18] proposed several techniques including ANNs and linear/multi-linear regression for the development of a field-calibration model of multiple sensors in order to measure gas air pollutants such as NO
2, O
3, CO, carbon dioxide (CO
2), and nitrogen oxide (NO). They have evaluated and compared each model using data spanning five months from a semi-rural site under varying conditions. The study found that the ANN technique had the best agreement between the sensor and reference instrument compared to the linear and multi-linear regression technique.
Although ANN techniques offer some advantages, they still have limitations, especially in regard to the local minima problem and the difficulty in determining a suitable structure model [
23]. Thus, several authors e.g., [
24,
25] have proposed either a new learning algorithm or have created a new technique to overcome the above limitations and to increase the reliability and accuracy of the ANN. In line with this development, integration between ANNs and the other techniques such as fuzzy logic is possible, leading to a new technique, namely the adaptive neuro fuzzy inference system (ANFIS) [
26]. The ANFIS has combined the advantages of both techniques into a single framework. It has the capability to extract information from human expert knowledge as well as data measured into linguistic information automatically and has the ability to adapt with new environmental knowledge, making it convenient for controlling sensors, pattern recognizing and forecasting tasks [
26]. The main purpose of this study is motivated by a desire to develop a LAQS system known as DiracSense for surface O
3, NO
2 and CO measurement. The sensor will be calibrated using laboratory and field test experiments. Finally, the ANFIS technique is used as the calibration model. In addition, an ANN approach, namely MLP, is used to assess the capability of the ANFIS as the calibration model.
2. Methods
2.1. DiracSense System
2.1.1. General Overview
The specific requirements for our sensing system were reliability and durability, that it is low-cost, portable, and easy to install by the user. Our system was designed to measure gas pollutants that are indexed by Malaysian ambient air quality standards at typical ambient concentrations. The result of our prototype development is DiracSense, as shown in
Figure 1. DiracSense collects, analyzes and shares air quality data using wireless communication. Using the Internet of Things (IoT) scenario allows data to be sent remotely to a web server such as Google drive or Dropbox periodically as well as the visualization of numerical and graphical values over time. An Android mobile phone application was used to display the data to facilitate users in obtaining air quality data.
2.1.2. Structure Design
The main part of DiracSense is in the form of a programmable system on a single board computer known as Raspberry Pi. This is the part of DiracSense which initializes all the software protocols required for the operation of the instrument. Looking at the structure of DiracSense (
Figure 2), the component that was embedded can be divided into four parts: the sensing unit; the analogue digital converter (ADC) unit; the processing and storage unit; and the transmission unit and power supply.
The DiracSense has three 4-electrode electrochemical or EC sensors and one built-in and one external meteorological sensor manufactured by Alphasense (Alphasense Ltd., Great Notley, Braintree, UK) and Vaisala (Helsinki, Findland), respectively. The EC sensors are used for the measurement of gas pollutants such as CO, NO
2 and O
3, as shown in
Table 1, while the meteorological parameters including pressure (P), temperature (T), and relative humidity (RH) are measured by a PTU300 sensor. The EC sensors used in our system were chosen such that they satisfy the concentration range and measurement accuracies required for ambient application while not compromising on the low power consumption requirements. The analogue output signals from the EC sensors are converted to digital signals via an onboard ADC before being fed to a single board computer. Signal/data processing, storage and transmission are also performed by the single board computer. Other hardware includes an 802.11 b/g/n wireless LAN and Bluetooth 4.1 used for the IoT. A 12 VDC battery integrated with solar power and DC/DC converter is used for the power supply unit.
Figure 2 presents the design flowchart of the DiracSense, where the main components with the main measurement system are highlighted.
2.1.3. EC Sensors
The EC sensors are operated in amperometric mode, meaning the current resulting from the redox reaction is proportional to the concentration of the target gas. The current is measured using suitable electronics in a potentiostat configuration and has either a linear or logarithmic response [
11]. Typically, the EC sensor consists of a cell made up of three electrodes which are separated with wetting filters. The filters are hydrophilic separators allowing the electrodes to come into contact with the electrolyte as well as allowing transport of the electrolyte through capillary action [
13]. However, AlphaSense have developed an electrochemical sensor which consists of four electrodes designated working, reference, counter and auxiliary electrodes.
The sensing electrodes are the working and counter electrodes, both of which serve as sites of redox reaction. These electrodes are coated with selected high-surface-area catalyst materials that facilitate optimal reaction mechanisms as well as providing selectivity towards the target gas species. The oxidation/reduction reaction at the working electrode is balanced with a complementary reduction/oxidation reaction at the counter electrode (this is characteristic of a complete redox reaction) [
13]. The redox pair results in the transfer of electrons (flow of current) between the working and counter electrodes. The reference electrode is used to stabilize and maintain the working electrode at a constant potential; this process ensures sensor response linearity over the range of uses. The auxiliary electrode (in a 4-electrode EC) is designed exactly like the working electrode except it is not in contact with the target gas species; as such it provides information on the effect of temperature on the overall recorded signal [
15].
These sensors are declared to have lower detection limits and, power low power consumption. Other desired qualities include relatively fast response times (<20 s) and less sensitivity to changes in interfering gases and environmental conditions compared to other types of low-cost sensors such as metal-oxide-semiconductor (MOS) sensors. However, they are also larger in size and more expensive (<
$100) [
11,
12].
2.2. Machine Learning
2.2.1. Adaptive Neuro Fuzzy Inference System
An adaptive neuro fuzzy inference system (ANFIS) is a machine learning modeling technique introduced by Jang [
26]. Its concept uses the intelligent hybrid method which integrates a neural network and fuzzy inference system (FIS). Typically, the ANFIS structure has functionality equivalent with the Takagi-Sugeno First-Order fuzzy model, wherein its construction is based on three conceptual frameworks including a rule base, a membership function (MF) and a fuzzy reasoning [
20]. In a FIS the most difficult part is obtaining a MF and rule base. There is no procedural or protocol standard to construct these using the trial-and-error method. Thus, the capability of the neural network can be used to adjust these parameters. Using a self-learning algorithm, the parameters of the MF and rule base are adjusted in adaptive form. Fuzzy logic deals with its capability on the decision and uncertainties due to its structured knowledge-based representation. Neural networks are known for their self-organization and learning ability. Thus, an ANFIS has the advantages of both neural network and fuzzy logic capability.
The ANFIS structure is related to the multilayer feed-forward network without weight in the network. The number of layers is fixed (about five layers) which represents the function of a fuzzy inference system, as shown in
Figure 3. The first and fourth layers are made up of the fuzzy set parameter (called the premise parameter) and the linear parameter of rule (called the consequent parameter). These parameters can be adjusted using the learning algorithm to reduce the network error. The remaining layers are fixed parameters which contain the evaluation process.
Each layer has different functions; a brief explanation about the layers is as follows: The first layer contains a node which functions to produce a membership grade of the input layer using the MFs grade of the Fuzzy set. Usually, the gauss and generalized bell MFs are considered in this node. Every MF has parameter sets—called premise parameters—with the ability to change the shape of the MF. As the premise parameter values change, the shape of the MFs will vary accordingly. The second layer consists of a fixed node, where this node is multiplies all incoming signal across the entire node and evaluates it via an operator (T-norm operator) to obtain the signal output. This procedure is known as the firing strength of a rule. The third layer, or the normalized firing strength procedure, is a layer which consists of a calculation ratio for each firing strength with the sum of all firing strengths. The calculation of the network output is conducted with the linear equation formula by multiplying the normalized firing strengths and weight averages of each rule. These procedures are performed in the fourth and fifth layers.
As mentioned, there are two key parameters (the premise and consequent parameters) which are adjustable in order to reduce the error of model. In this study, the hybrid learning algorithm introduced by Jang [
26] is used to optimize these parameters. This algorithm is expanded from the combination of the gradient descent or backpropagation learning algorithms with the least squares estimates (LSE). There are two steps that should be performed in this learning algorithm. The first step is forward passing, where the consequent parameter value is updated by the LSE. At the same time, the premise parameters in the first layer are fixed-rate and then the error-rate will pass backward. On the other hand, the gradient descent is used during the second step to improve the premise parameters by minimizing the overall sum of the squared errors.
In order to optimize the number of MFs and the rule in the ANFIS model, fuzzy clustering is employed to generate MFs and the rule base automatically. Increasing the number of MFs on the network will affect the number of controlling rules and consequently computation can be time-consuming. Moreover, the fuzzy clustering method has the capability to avoid the uncertainty of data grouping [
21]. With fuzzy clustering, the number of MFs and rules on the network is related to number of clusters that are generated. In this part, fuzzy subtractive clustering (FSC) is proposed as the fuzzy clustering method. FSC is very useful since as the number of clusters is not fixed it can automatically define the number of clusters based on the density of data points, which refers to the neighborhood radius value.
2.2.2. Artificial Neural Network
Artificial neural networks, known as ANNs, are popular modelling techniques that are frequently used in many applications related to scientific, engineering, medical, socio-economic, image processing and mathematical modelling [
27]. A multi-layer perceptron (MLP) is a type of ANN structure and is used in this study. This structure has been frequently used to develop models which have very complex functions appropriate for the calibration of sensors. In general, the MLP has a feed-forward structure containing of input, hidden and output layers, as shown in
Figure 4.
The work flow of the MLP is one direction, the information comes to the first layer (the input layer) before passing across the hidden layer and then to the last layer (the output layer). In addition, the structure of the MLP uses weighted sum of the input to produce the activation unit. This activation will be passed to the activation function to obtain the output in the output layer. By determining the number of layers and nodes in each layer, as well as the weights and thresholds of the network properly, it will minimize errors made by the network. This is part of the learning algorithm carrying out either supervised or unsupervised learning to optimize the result.
In this study the Levenberg-Marquardt learning algorithm, which is most commonly used for training [
28], was employed to automatically adapt the value of weights and thresholds on the MLP network in order to minimize the output of error. The error of a specific configuration of the network can be found via test performances of all the training cases implemented on the network, then comparing the actual output generated by the network with the target or desired outputs. The differences of output units are calculated to give an error network value as a sum squared error, where the individual error of each layers is squared and summed at the same time. Further details about this algorithm can be found in [
28].
2.3. Laboratory Calibration
As mentioned in
Table 1, the variants of EC sensors used in this study are CO-AF, OX-AF and NO
2-AF sensors for CO, O
3 and NO
2, respectively. These variants were designed to measure at low mixing ratios (units of parts per billion volume, ppb to few tens of parts per million volume, ppm range), achieved by the manufacturer improving both the sensitivity and sensor signal-to-noise ratio [
13]. As part of the sensor performance tests, laboratory tests for all gases were conducted at the Center for Atmospheric Science, Chemistry Department, University of Cambridge (Cambridge, UK).
Concentrated gas standards supplied by Air Liquide UK Ltd. (Air Liquide UK Ltd., Wolverhampton, UK) and high-purity zero air were used to conduct laboratory testing of sensor performance at ppb mixing ratios. Zero air was generated using a Model 111 Zero Air Supply instrument (Thermo Fisher Scientific, Franklin, MA, USA). This is done by scrubbing ambient air of trace gas species such as CO, NO, NO2, O3, SO2 and hydrocarbons using a Purafil (Purafil Inc., Doraville, GA, USA) and catalytic purification system. The gas standard containing 20 (±2%) ppm NO, NO2, SO2 and 200 (±2%) ppm of CO in N2 was diluted to lower mixing ratios by mixing with zero air using the Thermo Scientific Model 146i Multi-Gas Calibrator which also produces the O3 used in the calibration procedure.
A two-point (zero and span) calibration was conducted for CO, NO, O3 and NO2 at a flow rate of 4 L/min. The target mixing ratios used were 1100 ppb (parts per billion by volume), 392 ppb, 425 ppb and 388 ppb for CO, NO, NO2 and O3, respectively. Calibration gas mixing ratios were typical of those expected to be present in the urban environment. These mixing ratios were confirmed using Thermo Scientific analyzers, models 48i, 42i and 49i for CO, NO/NO2 and O3 respectively. Test gases were delivered to the sensors using a special Teflon-based manifold to reduce the T90 acquisition time. Although the sampling time for each sensor was 1 s, data were averaged to give 10 s measurements.
The model provided by the sensor manufacturer to translate the voltage signal from the electrodes of EC sensor to mixing ratio is presented in Equation (1):
where Y is the mixing ratio of target gas measured by EC sensor in units of ppb. WE (working electrode) and AE (auxiliary electrode) are the measured signal in millivolts (mV) for the two electrodes, WE
T and AE
T are the total zero offset of WE and AE (mV), respectively, corresponding to the signals recording during the zero-air calibration. The last parameter S
T, is the total sensitivity of EC sensor (mV/ppb). WE
T, AE
T and S
T were provided by the sensor manufacturer.
With these tests, we can assess the reliability of the calibration parameters (including the cross-interference information for Ox sensor) provided by the sensor manufacture and if necessary generate new correction factors.
2.4. Field Campaign
The measurement campaign was conducted at the research building complex, Universiti Kebangsaan Malaysia (UKM, Bangi, Malaysia) from 9–29 December 2017. This study only involved an O3 comparison as there were no other reference instrumentation at the study location. A model Serinius 10 UV photometric analyzer (EcoTech, Melbourne, Australia) was used in this campaign as the reference instrument for surface O3. This analyzer was well maintained and had been calibrated prior to this campaign. The calibration was performed based on a 7-point standard from low to high concentrations, with a range of interest of 0.1 to 200 ppb and detection limits of 0 to 50 ppb. During this campaign, DiracSense was located close to the inlet of the reference instrument to ensure good co-location.
One important step when developing a model using the soft computing technique is selecting the input variable and the size of the training data set, as they have capability to influence the determination of the network and the strength of model [
24]. Generally, the training data are used as a knowledge base and the rules of the model in order to catch all characteristics of the target. Two other types of data are also used in this developing stage, including the validation and testing data. The validation data are used to make certain that the model is trained to have the capability to generalize training data in order to represent the target data to avoid overfitting during the training period. The overfitting will occur if the model is trained too much, causing the model to lose its ability to generalize and adjust any data that was not included in training process [
20]. At the same time, the testing data are used to check the performance capabilities of the resulting model.
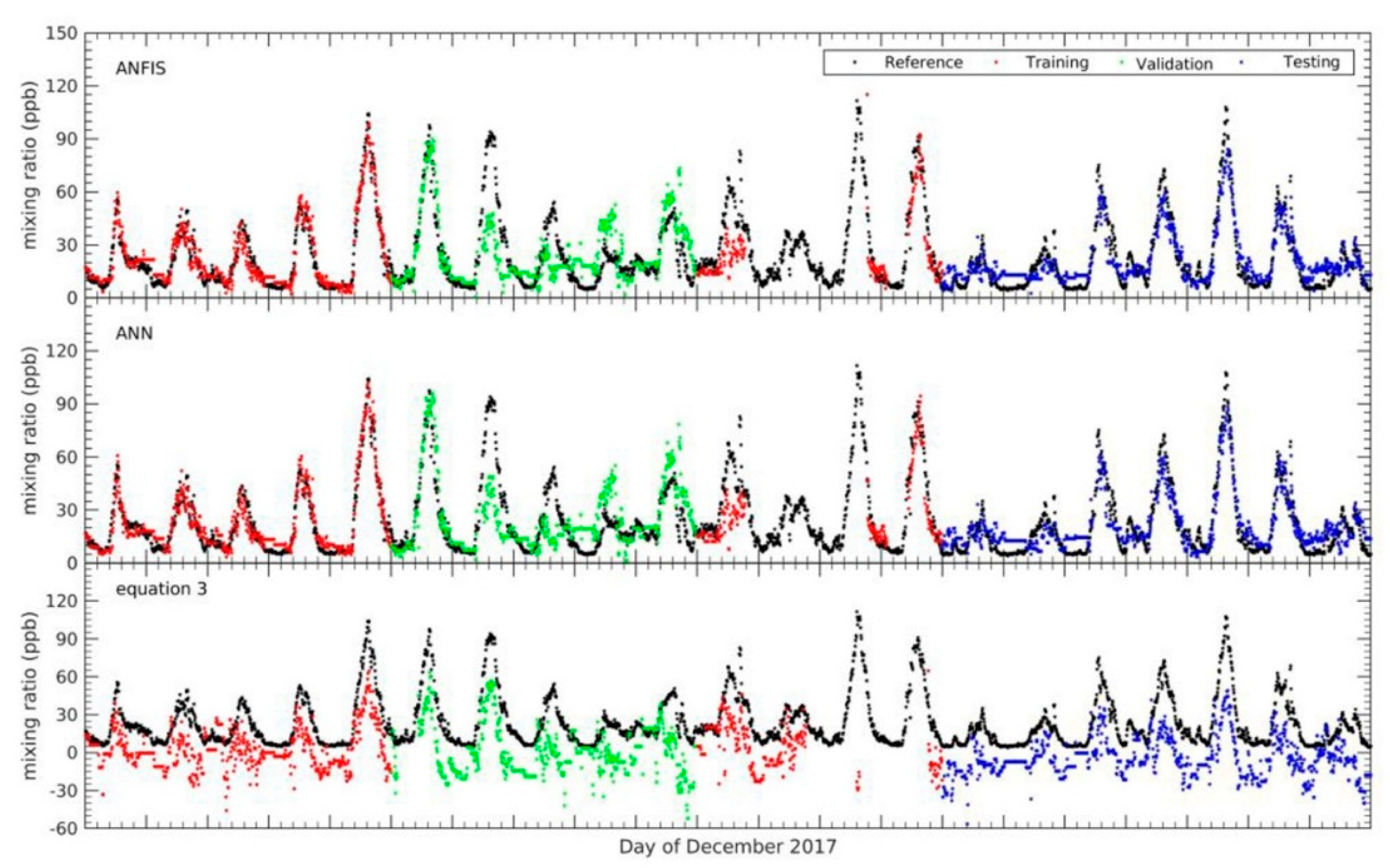
In this study, two source data sets (raw data from the EC sensor and the reference instrument) were applied in the developing model as input and target data, respectively. All data should be equal interval resolution data. Since the data from the O
3 reference instrument had a time resolution of 10 min, 10-min averaged raw data from DiracSense were used in order to equal the resolution of the data. All data collected were divided into three data subsets (training, validation and testing). The training data set was taken from 9–13 and 18–22 December, while the validation data spanned 14–17 December 2017. The remaining seven days (23–29 December 2017) were used for the testing data sets (see
Table 2). The cross-validation method was used to divide data into these three subsets. All the data sets during the training period were quality controlled to exclude invalid or noise data flagged in the recorded raw data as Not a Number (NaN).
The configuration input models used for the calibration model are shown in the
Table 3. The configuration input model consisted of working and auxiliary electrodes raw data (WE OX, and AE OX), NO
2 gas and T data from the OX-A431 EC sensor, NO
2-A43F EC sensor, and temperature sensor respectively. These configurations were proposed to avoid the limitation of data availability and to investigate the impact of different combinations of the variables on the correction of EC sensor. Six combinations of the input variables (see
Table 3) were studied to investigate their effects on producing calibrated data from the EC sensor. The combinations make use of either two or four inputs. The choice of input variables in developing a calibration model is very important task as it can affect the performance of the model. Similarly, the size of the training data set is equally very vital, as it will affect the ability of the model in capturing all the characteristics of the desired output. In this study, we employed several statistical analysis techniques to evaluate the performance of the calibration model. These included the calculation of the coefficient correlation (r), percent error (PE) and root mean squared error (RMSE).
4. Conclusions
Three EC sensors from AlphaSense were constructed to measure CO, NO2, and O3. The sensors behaved highly linearly in laboratory experiments and had response times of around 0.5–1.6 min. During the laboratory experiment, a simple equation was used to translate the signal to mixing ratio and was calibrated by adding a correction in order to achieve the minimum difference against the gas standard. We found that with the added corrections such as the new sensitivity and offset to the equation, the difference values between mixing ratio of EC sensor and gas standard became decreased. Furthermore, this equation is deployed together with the other calibration model which constructed using the machine learning to translate signal to mixing ratios in the field experiment.
After the laboratory experiment was performed, field tests were undertaken to investigate the performance of the EC sensor when measuring gases in ambient conditions. However, due to the lack of other routine instruments at the UKM, the field calibration for the EC sensor focused on the mixing ratio of O
3. Several calibration models were constructed in order to improve the accuracy and performance of the EC sensor, including ANFIS, MLP and the simple equation which was calibrated during the laboratory experiment. This study has successfully demonstrated the capability of calibration models constructed using the ANFIS technique to improve the accuracy and performance of EC sensors in order to measure mixing ratios of O
3. Since the input parameter is one of the crucial components in developing a machine learning, few combination inputs were evaluated to obtain the best structure input network for the ANFIS in order to obtain high accuracy. This is parallel with the other studies, wherein the correctly input selection as well as it has correlated with the target output interest will be affected on the performance of model, especially in the local minima problem [
18,
19]. From the configuration input combination, we found that the combination input with only the mixing ratio of NO
2 was not able to translate the output signal of the EC sensor to the mixing ratio of O
3 correctly. However, adding new input variables such as WE OX, AE OX and T will gradually improve the calibration model developed using ANFIS. The combination of input variables containing WE OX, AE OX, T, and NO
2 were the best selection in terms of configuration input network for the calibration model. Moreover, the input combination containing WE OX, AE OX and T can be an optional configuration input network when mixing ratio of NO
2 data are limited.
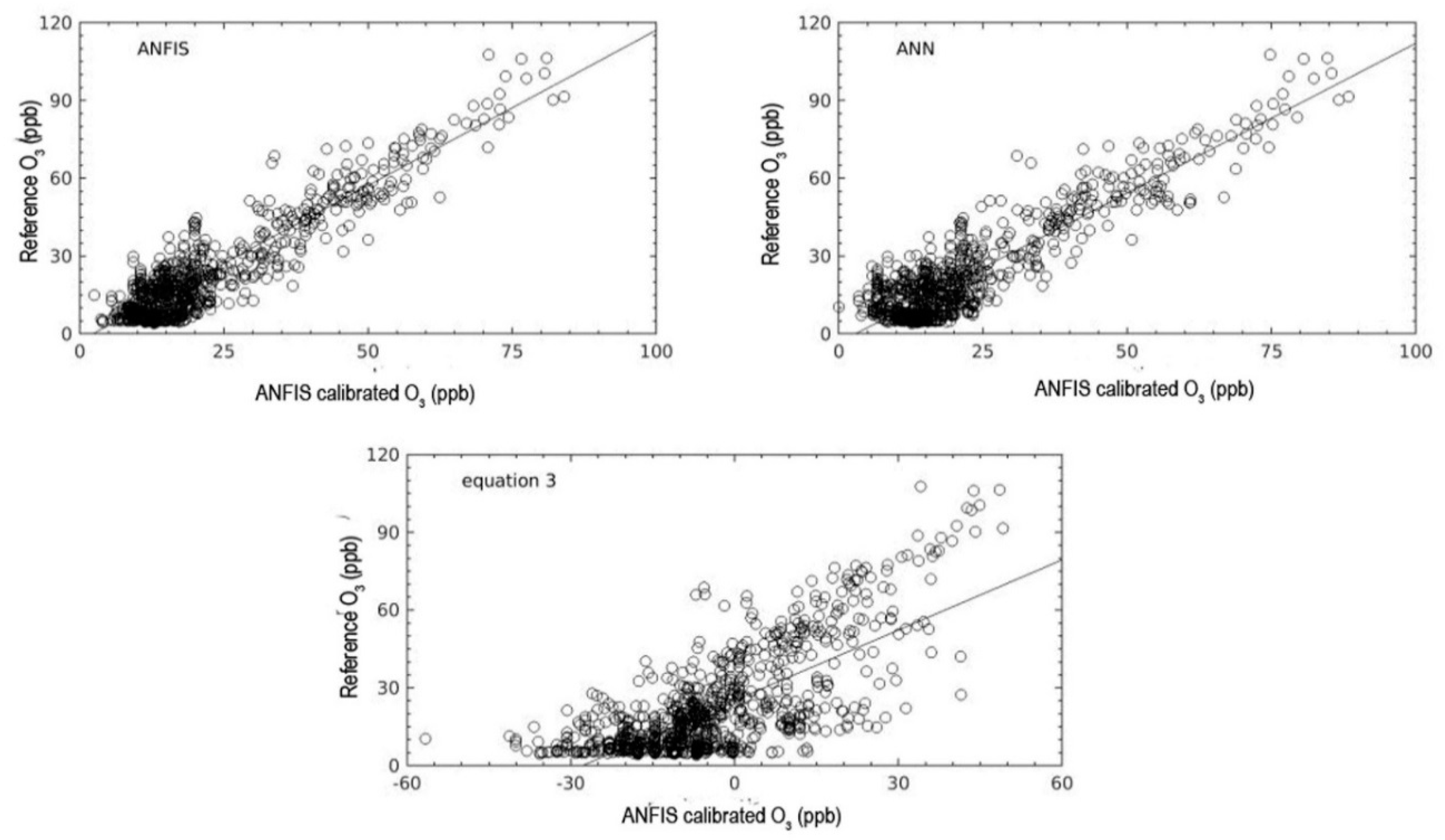
Other models were tested, and the results demonstrated that the calibration model constructed using MLP has potential as a competitive model to ANFIS. It had the second-strongest coefficient correlation. However, the calibration model using the ANFIS technique still outperformed the other models in terms of the statistical evaluation criteria. The calibration model constructed using ANFIS had the lowest RMSE and MAE values as well as the highest correlation coefficient during the validation period.
Nevertheless, it should be noted that the representatives of measurements in this result only showed during the conditions of this campaign. The result may be different for longer time periods, since the model experiment was only conducted for seven days during the validation period. Moreover, this calibration model should be regarded as the on-site calibration since it required ground-based data as the target data for the area of deployment. It very hard to claim this model can be used as a generalized calibration model since the environments of polluted areas have different variations. In addition, the ageing of sensors is required to be considered since it leads to decreasing sensor performance [
29]. However, this model can be deployed in other areas of interest if the conditions are similar or the process would be adding more knowledge into the model.
Regardless, the calibration model constructed using machine learning including ANFIS and MLP has a usable ability to improve the accuracy and performance of EC sensors in terms of measuring mixing ratios of O3. It will beneficial for researchers and communities who want to measure the O3 in the air for air quality monitoring purposes using the low-cost sensor since the results showed that it was in close agreement with the reference instrument.