Research on Distributed 5G Signal Coverage Detection Algorithm Based on PSO-BP-Kriging
Abstract
:1. Introduction
- Distributed sensor nodes are randomly deployed to collect the received signal strength indicator (RSSI) of 5G communication base station, and the collected data are pre-processed by Gaussian filtering, which reduces the influence of error on the performance of the algorithm.
- The Delaunay triangulation algorithm is used to mesh the target area, and the selection of interpolation points is realized.
- An improved hybrid interpolation algorithm is proposed to estimate the RSSI value of the interpolation point. The objective function of backpropagation (BP) neural network is modified by the variogram of Kriging interpolation and improved particle swarm optimization (PSO) algorithm, which overcomes the overly smooth spatial expression of traditional Kriging interpolation and local convergence of BP neural network interpolation.
- The data collected by the sensor node and the data estimated by the interpolation point are processed comprehensively, then the coverage area situation of the 5G mobile communication network is generated, realizing the reproducible real-time detection of the wireless network coverage.
2. Related Work
3. Algorithm Description
3.1. The Principle of Kriging Interpolation
3.2. The Principle of BP Neural Network Interpolation
4. 5G Mobile Communication Network Coverage Detection Algorithm
4.1. Data Preprocessing
4.2. Hybrid Interpolation Optimization Algorithm
4.2.1. Objective Function Establishment
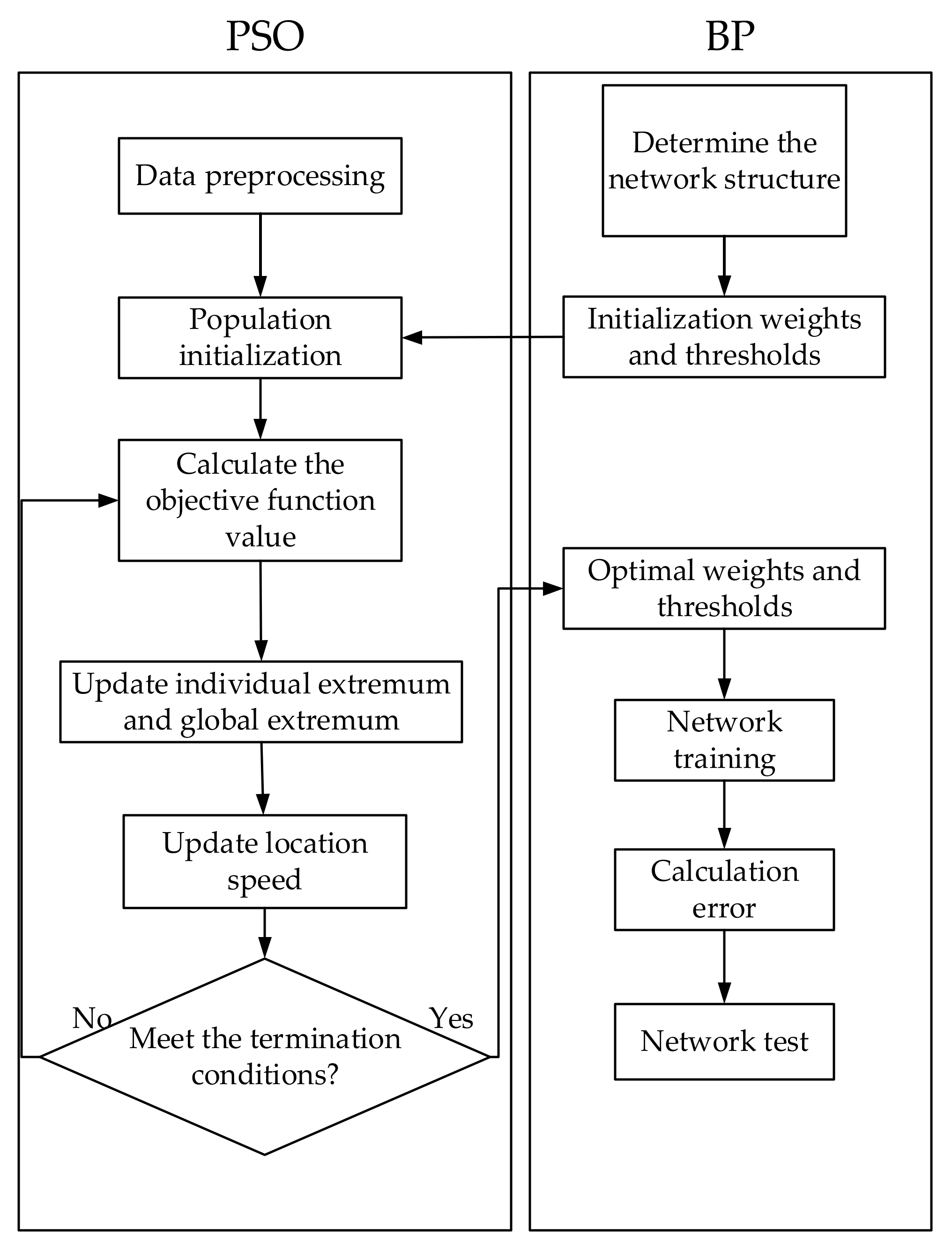
4.2.2. Improved Particle Swarm Optimization Algorithm for BP Neural Network
- (1)
- Particle initialization;
- (2)
- Calculate the value of fitness function;
- (3)
- Find the optimal values of individuals and groups;
- (4)
- Update the speed and position of particles. If the set maximum number of iterations is reached in advance during the optimization process, it stops and outputs the optimal solution at this time. Otherwise, turn to the second step and continue to execute the loop;
- (5)
- Obtain the optimal weight and threshold and assign it to the BP network;
- (6)
- Calculate the error of the BP network model. If the error does not reach the target value, continue to update the weight and threshold of the network until the condition is met.
4.2.3. Hybrid Interpolation Optimization Algorithm Steps
- (1)
- Calculate by using sample data and select the appropriate model to fit it;
- (2)
- Determine the network structure. Including learning factors, learning rates, target errors, and maximum number of iterations;
- (3)
- Calculating the variogram in Equation (12) according to the separation distance and the corresponding of different sensor node pairs;
- (4)
- Use the PSO algorithm to determine the initial weight of the neural network;
- (5)
- Calculate the network output according to Equation (7);
- (6)
- Update the next iteration weight according to the equation ( is the learning factor and is the learning rate coefficient);
- (7)
- Use the error between the network output and the sample, and , to calculate from Equation (12);
- (8)
- If , the weight at this time is the last weight of the network, otherwise, turn to step (4);
- (9)
- Select other samples to test the fitting performance of the network. If the conditions are met, proceed to the next step, otherwise turn to step (4);
- (10)
- Interpolation estimation is performed by using a trained network.
4.3. 5G Mobile Communication Network Coverage Area Situation Generation
5. Simulation Experiment Analysis
5.1. Simulation Environment Construction
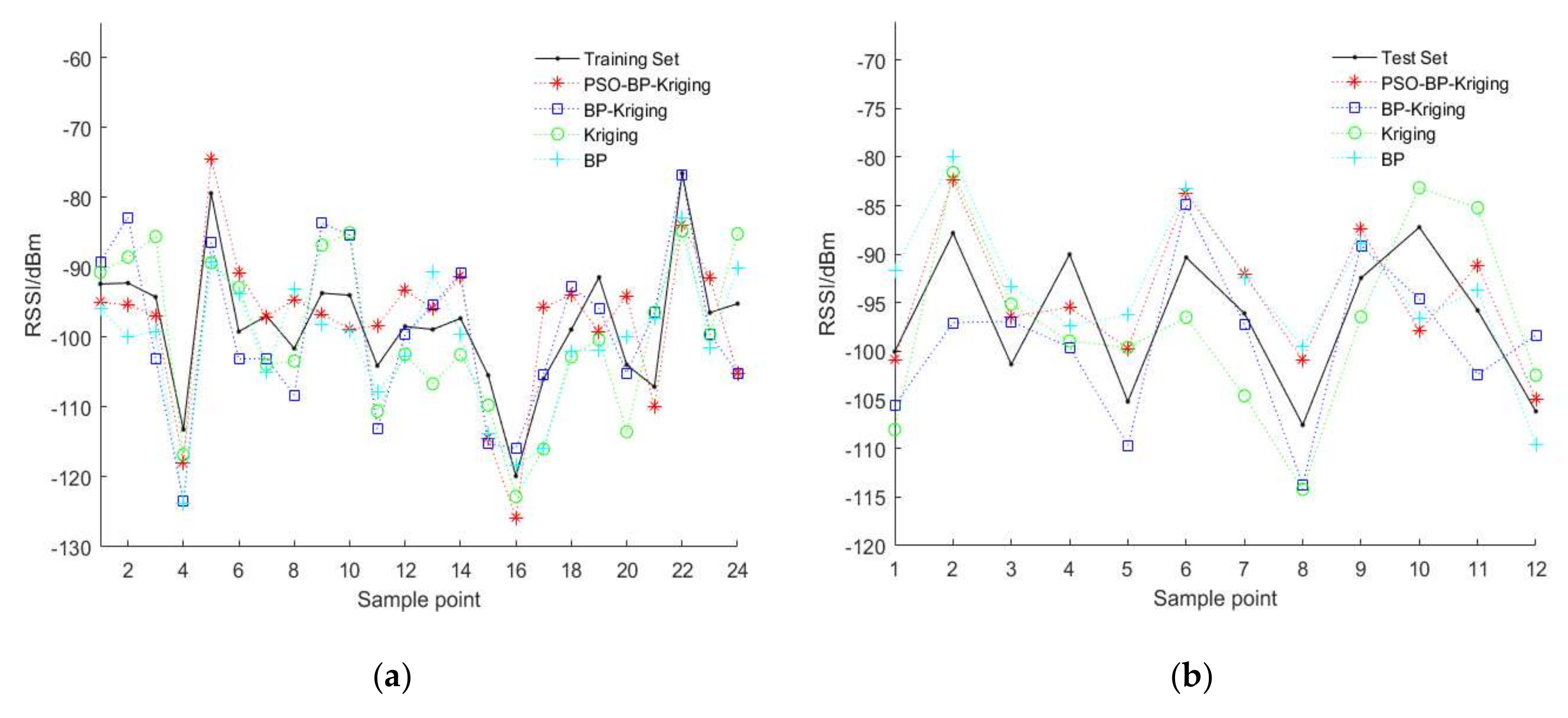
5.2. Predictive Model Performance Analysis
5.2.1. Predictive Model Accuracy Comparison
5.2.2. Algorithm Suitability Analysis
5.3. Performance Analysis of Interpolation Optimization Algorithm
5.4. Coverage Situation Generation of 5G Network
5.5. Algorithm Validity Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Table of Abbreviations
| Abbreviation | Full Name |
| 5GNOW | 5th Generation Non-Orthogonal Waveforms for Asynchronous Signaling |
| METIS | Mobile and Wireless Communications Enablers for the Twenty-Twenty Information Society |
| 5G PPP | 5G Public-Private Partnership |
| RSSI | Received Signal Strength Indicator |
| PSO | Particle Swarm Optimization |
| BP | Back Propagation |
| PSO-BP | Particle Swarm Optimization BP Neural Network |
| BP-Kriging | Kriging-BP Neural Network |
| PSO-BP-Kriging | Particle Swarm Optimization and Kriging -BP Neural Network |
| RMSE | root mean square error |
Appendix A.2. Comparison Table of Related Work
| Method | Characteristics | Difference |
| Signal propagation model | Low computational complexity | Low precision, existing models are not applicable |
| Newton interpolation | High precision | High computational complexity |
| IDW interpolation | High precision when interpolating points are dispersed | Poor spatial correlation, large amount of calculation |
| Kriging interpolation | Good spatial correlation and high precision | Spatial local features are masked |
| BP neural network | High precision | Poor spatial correlation, local convergence |
| PSO-BP model | Higher precision | Poor spatial correlation |
| BP-Kriging model | Good spatial correlation and high precision | Local convergence |
Appendix A.3. Mathematical Calculations and Derivations
- (1)
- Determine the hidden layer and the number of nodes per layer;
- (2)
- Determine the network structure;
- (3)
- Input sample data;
- (4)
- Calculate the output value of each layer node according to the node function Equation (A13);
- (5)
- Modify the weight of the th iteration;
- (6)
- Calculate the error of the network output value and the expected output value, where is the expected value of the output of the j-th component of the p-th sample, and is the network output value, and when the objective function value is less than the given allowable error , the learning process ends, completing the training process of the network, otherwise return to step (3);
- (7)
- Select different samples from the training set to detect the generalization ability of the network. If the error between the network output value and the actual value of the detected sample is within the allowable range, the network training quality meets the requirements. Otherwise, re-adjust the parameters and repeat the above network training until the network training error meets the requirements.
References
- Prados, J.; Ramos-Munoz, J.J.; Ameigeiras, P.; Andres-Maldonado, P. Modeling and dimensioning of a virtualized MME for 5G mobile networks. IEEE Trans. Veh. Technol. 2017, 66, 4383–4395. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Imran, M.A.; Evans, B. Energy efficient hybrid satellite terrestrial 5G networks with software defined features. J. Commun. Netw. 2017, 19, 147–161. [Google Scholar] [CrossRef]
- 5GNOW. 5th Generation: Non-Orthogonal Waveform of Asynchonous Signaling. 2015. Available online: http://www.5gnow.eu (accessed on 18 September 2015).
- METIS. Mobile and Wireless Communications Enablers for the Twenty-Twenty Information Society. EU7th Framework Program Project. 2015. Available online: http: //www.metis2020.com (accessed on 18 September 2015).
- IMT-2020 (5G) PG. White Paper on 5G Vision and Requirements. 2015. Available online: http://www.imt-2020.cn/zh/documents/listByQuery?current Page=1&content (accessed on 18 September 2015).
- Series, M. IMT Vision-Framework and Overall Objectives of the Future Development of IMT for 2020 and Beyond; Recommendation ITU: Geneva, Switzerland, 2013. [Google Scholar]
- ICT-317669 METIS Project. Scenarios, Requirements and KPIs for 5G Mobile and Wireless System. Huawei ERC: Hong Kong, China, 2013. [Google Scholar]
- Nokia Siemens Networks. 2020: Beyond 4G Radio Evolution for the Gigabit Experience; White Paper; Nokia Siemens Networks: Espoo, Finland, 2011. [Google Scholar]
- Ericsson. More than 50 Billion Connected Devices; White Paper; Ericsson: Stockholm, Sweden, 2011. [Google Scholar]
- Fettwweis, G.; Alamouti, S. 5G: Personal mobile internet beyond what cellular did to telephony. IEEE Commun. Mag. 2014, 52, 140–145. [Google Scholar] [CrossRef]
- Osseiran, A.; Boccardi, F.; Braun, V.; Kusume, K.; Marsch, P.; Maternia, M.; Queseth, O.; Schellmann, M.; Schotten, H.; Taoka, H.; et al. Scenario for 5G mobile and wireless communication: The vision of the METIS project. IEEE Commun. Mag. 2014, 52, 26–35. [Google Scholar] [CrossRef]
- Wang, C.X.; Haider, F.; Gao, X.; You, X.H. Cellular architecture and key technologies for 5G wireless communication networks. IEEE Commun. Mag. 2014, 52, 122–130. [Google Scholar] [CrossRef] [Green Version]
- You, X.H.; Pan, Z.W.; Gao, X.Q.; Cao, S.M. The 5G mobile communication: The development trends and its emerging key techniques. Sci. China Press 2014, 44, 551–563. [Google Scholar] [CrossRef]
- Aayapong, P.; Iwamura, M.; Staehle, D.; Kiess, W. Design considerations for a 5G network architecture. IEEE Commun. Mag. 2014, 52, 65–75. [Google Scholar] [CrossRef]
- Mohammad, A.N.; Walid, M.D.; Tapan, K.S. Further Validation of an Electromagnetic Macro Model for Analysis of Propagation Path Loss in Cellular Networks Using Measured Driving-Test Data. IEEE Antennas Propag. Mag. 2014, 56, 108–129. [Google Scholar] [CrossRef]
- Sun, B.; Feng, Q.K.; Jin, X.Y.; Wu, D.P. Handoff algorithm and PoSC model under high-speed railway environment. J. Zhejiang Univ. 2012, 46, 1553–1559. [Google Scholar] [CrossRef]
- Chen, Z.S.; Shen, H. Energy-efficient Multi-hop Routing Protocol for Wireless Sensor Networks. Comput. Sci. 2015, 42, 90–94. [Google Scholar] [CrossRef]
- Vincent, S.; Alexandre, S.; Yves, L. Theoretical bit error floor analysis of 16-QAM OFDM signal with channel estimation using polynomial interpolation. IET Signal Process. 2016, 10, 254–265. [Google Scholar] [CrossRef]
- Shang, F.J.; Su, W.; Wang, Q.; Gao, H.X.; Fu, Q. A location estimation algorithm based on RSSI vector similarity degree. Int. J. Distrib. Sens. Netw. 2014, 10, 350–371. [Google Scholar] [CrossRef]
- Lyudmila, M.; Arshad, A.; Bamidele, A.; Augustine, I. Location prediction optimisation in WSNs using Kriging interpolation. IET Wirel. Sens. Syst. 2016, 6, 74–81. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.; Zhang, J.; Dong, Y.; Pan, J. Realization on indoor positioning in basis of reference tag. Int. J. Wavelets Multiresolution Inf. Process. 2014, 12, 1–10. [Google Scholar] [CrossRef]
- Mrinmoy, S.; Indrajit, B.; Mainak, C.; Tuhina, S. A node deployment mechanism accounting into received signal strength and frequency diversity for a wireless sensor network. In Proceedings of the IEEE SENSORS, Orlando, FL, USA, 30 October–3 November 2016; pp. 1–3. [Google Scholar]
- Evangelos, Z.; Dimitris, T.; Adrian, M.; Nikos, D. Multiterminal source coding with copula regression for wireless sensor networks gathering diverse data. IEEE Sens. J. 2017, 17, 139–150. [Google Scholar] [CrossRef]
- Wu, D.J.; Xia, L.Y. Reference Device-Assisted Adaptive Location Fingerprinting. Sensors 2016, 16, 802. [Google Scholar] [CrossRef] [PubMed]
- Zuo, J.B.; Liu, S.; Xia, H.; Qiao, Y.Y. Multi-Phase Fingerprint Map Based on Interpolation for Indoor Localization Using iBeacons. IEEE Sens. J. 2018, 18, 3351–3359. [Google Scholar] [CrossRef]
- Wang, G.; Genter, G.; Parysow, P. Spatial prediction and uncertainty analysis of topographic factors for the revised soil losses equation (RUSEL). J. Soil Water Conserv. 2000, 55, 374–384. [Google Scholar] [CrossRef]
- Ko, C.N.; Chang, Y.P.; Wu, C.J. A PSO method with nonlinear time-varying evolution for optimal design of harmonic filter. IEEE Trans. Power Syst. 2009, 23, 437–444. [Google Scholar] [CrossRef]
- Sainath, T.N.; Weiss, R.J.; Wilson, K.W.; Li, B. Multichannel signal processing with deep neural networks for automatic speech recognition. IEEE/ACM Trans. Audio Speech Lang. Process. 2017, 25, 965–979. [Google Scholar] [CrossRef]
- Chagas, S.H.; Martins, J.B.; Oliveira, L.L.D. Genetic Algorithms and Simulated Annealing optimization methods in wireless sensor networks localization using artificial neural networks. IEEE Int. Midwest Symp. Circuits 2012, 928–931. [Google Scholar] [CrossRef]
- Li, Z.; Luo, L.G.; Liu, Y.D.; Sheng, G.H. UHF partial discharge localization algorithm based on compressed sensing. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 21–29. [Google Scholar] [CrossRef]
- Jia, Z.Y.; Zhou, S.L.; Su, Q.L.; Wang, J.X. Comparison Study on the Estimation of the Spatial Distribution of Regional Soil Metal(loid)s Pollution Based on Kriging Interpolation and BP Neural Network. Int. J. Environ. Res. Public Health 2018, 15, 34. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, Q. Data-Driven Fault Diagnosis Method for Power Transformers Using Modified Kriging Model. Math. Probl. Eng. 2017, 2017, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Koike, K.; Matsuda, S.; Gu, B. Evaluation of interpolation accuracy of neural kriging with application to temperature distribution analysis. Math. Geol. 2001, 33, 421–448. [Google Scholar] [CrossRef]
- Ismail, A.; Jeng, D.S.; Zhang, L.L. An optimised product-unit neural network with a novel PSO–BP hybrid training algorithm: Applications to load–deformation analysis of axially loaded piles. Eng. Appl. Artif. Intell. 2013, 26, 2305–2314. [Google Scholar] [CrossRef] [Green Version]
- Bai, T.C.; Meng, H.B.; Yao, J.H. A forecasting method of forest pests based on the rough set and PSO-BP neural network. Neural Comput. Appl. 2014, 25, 1699–1707. [Google Scholar] [CrossRef]
- Li, Y.J.; Li, Y.H.; Li, F.; Zhao, B.; Li, Q.Q. The Research of Temperature Compensation for Thermopile Sensor Based on Improved PSO-BP Algorithm. Math. Probl. Eng. 2015, 2015, 1–6. [Google Scholar] [CrossRef]
- Tonnizam, E.; Jahed, A.D.; Momeni, E.; Yazdavar, A. Rock strength estimation: A PSO-based BP approach. Neural Comput. Appl. 2018, 30, 1635–1646. [Google Scholar] [CrossRef]
- Hou, C.G.; Yu, X.; Cao, Y.D.; Lai, C.X.; Cao, Y.C. Prediction of synchronous closing time of permanent magnetic actuator for vacuum circuit breaker based on PSO-BP. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 3321–3326. [Google Scholar] [CrossRef]
- Koya, S.; Takeo, F. Kriging-based interference power constraint: Integrated design of the radio environment map and transmission power. IEEE Trans. Cogn. Commun. Netw. 2017, 3, 13–25. [Google Scholar] [CrossRef]
- Song, X.; Mihai, R.; Jan, K.S. Adaptive weighted expected improvement with rewards approach in kriging assisted electromagnetic design. IEEE Trans. Magn. 2013, 49, 2057–2060. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, F.L.; Sun, T.; Xu, B. A constrained optimization method based on BP neural network. Neural Comput. Appl. 2018, 29, 413–421. [Google Scholar] [CrossRef]
- Jiang, Q.; Ma, Y.; Liu, K.; Dou, Z. A probabilistic radio map construction scheme for crowdsourcing-based fingerprinting localization. IEEE Sens. J. 2016, 16, 3764–3774. [Google Scholar] [CrossRef]
- Kurt, D.; Milos, M. Wireless sensor networks—Node localization for various industry problems. IEEE Trans. Ind. Inform. 2015, 11, 752–762. [Google Scholar] [CrossRef]
- Wang, H.B.; Zhao, X.Q.; Wang, K.Z.; Xia, K.J.; Tu, X.Y. Cooperative velocity updating model based particle swarm optimization. Appl. Intell. 2014, 2, 322–342. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R.C. A Modified Partical Swarm Optimizer. IEEE World Congr. Comput. Intell. 1998, 69–73. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Swarm Intelligence; Morgan Kaufmann Publisher: San Francisco, CA, USA, 2001; pp. 69–73. [Google Scholar]
- Zhou, T. Research on Several Key Techniques of Electromagnetic Situation Generation in Sea Battlefield [D]. Harbin Engineering University: Harbin, China, 2013. [Google Scholar]




| Simulation Parameters | Configuration Value |
|---|---|
| Target area size | 400 m × 400 m |
| Path loss model | Okumura-Hata |
| Standard deviation of shadow fading | 10 dB |
| Carrier frequency | 3.4 GHz |
| Network model | Three sector model |
| Number of users in each cell | 100 |
| Number of sensor nodes | 42 |
| Performance Parameter | PSO-BP-Kriging | BP-Kriging | Kriging | BP |
|---|---|---|---|---|
| RMSE | 5.9756 | 6.5979 | 6.7193 | 6.6218 |
| R2 | 0.6541 | 0.6173 | 0.6054 | 0.5946 |
| Method | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Road Test | −89.308 | −82.852 | −103.16 | −113.491 | −86.475 | −108.312 | −95.457 | −90.887 | −79.645 |
| Interpolation | −87.935 | −83.674 | −105.03 | −110.856 | −89.317 | −107.544 | −93.121 | −86.021 | −81.534 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, T.; Wang, H. Research on Distributed 5G Signal Coverage Detection Algorithm Based on PSO-BP-Kriging. Sensors 2018, 18, 4390. https://doi.org/10.3390/s18124390
Xiang T, Wang H. Research on Distributed 5G Signal Coverage Detection Algorithm Based on PSO-BP-Kriging. Sensors. 2018; 18(12):4390. https://doi.org/10.3390/s18124390
Chicago/Turabian StyleXiang, Tingli, and Hongjun Wang. 2018. "Research on Distributed 5G Signal Coverage Detection Algorithm Based on PSO-BP-Kriging" Sensors 18, no. 12: 4390. https://doi.org/10.3390/s18124390
APA StyleXiang, T., & Wang, H. (2018). Research on Distributed 5G Signal Coverage Detection Algorithm Based on PSO-BP-Kriging. Sensors, 18(12), 4390. https://doi.org/10.3390/s18124390





