A Comparative Study on Evolutionary Multi-objective Optimization Algorithms Estimating Surface Duct
Abstract
:1. Introduction
2. Multi-Objective Optimization Using Evolutionary Algorithms
2.1. Basic Concepts of Multi-Objective Optimization
2.2. Evaluation Metrics
2.3. Phase-Delay Model and Propagation-Loss
2.4. Parameterized Model
3. Performance Comparison
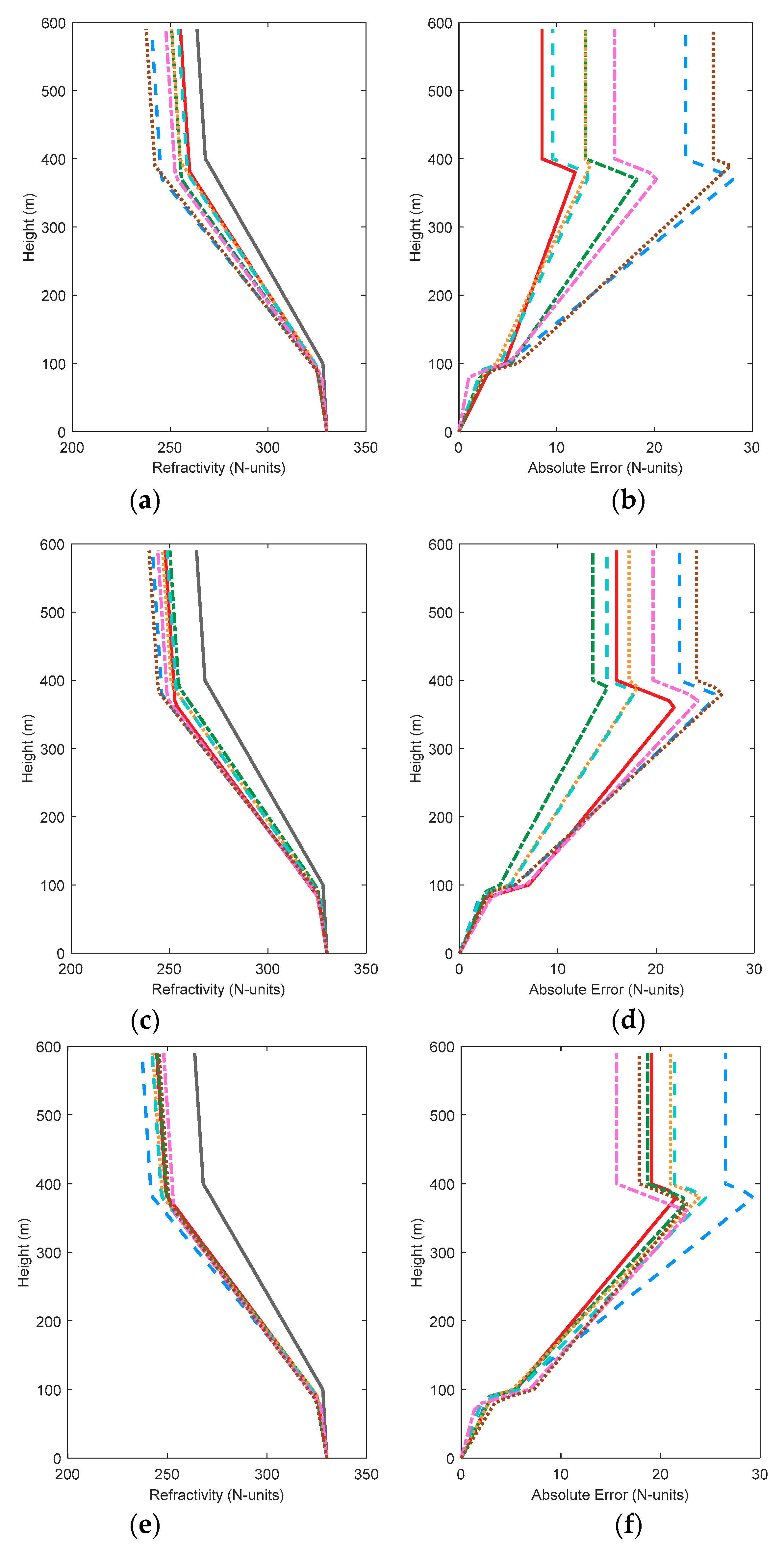
3.1. Excluding Antenna Height and Transmitting Frequency
3.2. Including Transmitting Frequency
3.3. Including Antenna Height and Transmitting Frequency
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gerstoft, P.; Gingras, D.F.; Rogers, L.T.; Hodgkiss, W.S. Estimation of radio refractivity structure using matched-field array processing. IEEE Trans. Antennas Propag. 2000, 48, 345–356. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Y.; Blahak, U.; Neuper, M.; Jerger, D. Radar Beam Tracing Methods Based on Atmospheric Refractive Index. J. Atmos. Ocean. Technol. 2014, 31, 2650–2670. [Google Scholar] [CrossRef]
- Shume, E.; Ao, C. Remote sensing of tropospheric turbulence using GPS radio occultation. Atmos. Meas. Tech. 2016, 9, 3175–3182. [Google Scholar] [CrossRef] [Green Version]
- Fountoulakis, V.; Earls, C. Duct heights inferred from radar sea clutter using proper orthogonal bases. Radio Sci. 2016, 51, 1614–1626. [Google Scholar] [CrossRef]
- Hallali, R.; Dalaudier, F.; Parent du Chatelet, J. Comparison between Radar and Automatic Weather Station Refractivity Variability. Bound. Lay. Meteorol. 2016, 160, 299–317. [Google Scholar] [CrossRef]
- Gerstoft, P.; Rogers, L.T.; Hodgkiss, W.S.; Wagner, L.J. Refractivity estimation using multiple elevation angles. IEEE J. Ocean. Eng. 2003, 28, 513–525. [Google Scholar] [CrossRef] [Green Version]
- Gerstoft, P.; Rogers, L.T.; Krolik, J.L.; Hodgkiss, W.S. Inversion for refractivity parameters from radar sea clutter. Radio Sci. 2003, 38. [Google Scholar] [CrossRef] [Green Version]
- Yardim, C.; Gerstoft, P.; Hodgkiss, W.S. Tracking Refractivity from Clutter Using Kalman and Particle Filters. IEEE Trans. Antennas Propag. 2008, 56, 1058–1070. [Google Scholar] [CrossRef] [Green Version]
- Sheng, Z. The estimation of lower refractivity uncertainty from radar sea clutter using the Bayesian—MCMC method. Chin. Phys. B 2013, 22. [Google Scholar] [CrossRef]
- Douvenot, R.; Fabbro, V.; Gerstoft, P.; Bourlier, C.; Saillard, J. A duct mapping method using least squares support vector machines. Radio Sci. 2008, 43, 1–12. [Google Scholar] [CrossRef]
- Karimian, A.; Yardim, C.; Gerstoft, P.; Hodgkiss, W.S.; Barrios, A.E. Refractivity estimation from sea clutter: An invited review. Radio Sci. 2011, 46, 1–16. [Google Scholar] [CrossRef]
- Zhao, X.; Huang, S. Atmospheric Duct Estimation Using Radar Sea Clutter Returns by the Adjoint Method with Regularization Technique. J. Atmos. Ocean. Technol. 2014, 31, 1250–1262. [Google Scholar] [CrossRef]
- Hitney, H.V. Remote sensing of refractivity structure by direct radio measurements at UHF. In AGARD, Remote Sensing of the Propagation Environment 6 p (SEE N92-22790 13-46); Naval Ocean Systems Center: San Diego, CA, USA, 1992. [Google Scholar]
- Anderson, K.D. Tropospheric refractivity profiles inferred from low elevation angle measurements of Global Positioning System (GPS) signals. In Proceedings of the AGARD Conference on Sensor and Propagation Panel Symposium, Bremerhaven, Germany, 19–22 September 1994; North Atlantic Treaty Organization: Neuilly-sur-Seine, France, 1995. [Google Scholar]
- Liao, Q.; Sheng, Z.; Shi, H. Joint Inversion of Atmospheric Refractivity Profile Based on Ground-Based GPS Phase Delay and Propagation Loss. Atmosphere 2016, 7, 12. [Google Scholar] [CrossRef]
- Liao, Q.; Sheng, Z.; Shi, H.; Xiang, J.; Yu, H. Estimation of Surface Duct Using Ground-Based GPS Phase Delay and Propagation Loss. Remote Sens. 2018, 10, 1–20. [Google Scholar] [CrossRef]
- Marseguerra, M.; Zio, E.; Podofillini, L. Optimal reliability/availability of uncertain systems via multi-objective genetic algorithms. IEEE Trans. Reliab. 2004, 53, 424–434. [Google Scholar] [CrossRef]
- Zamuda, A.; Brest, J.; Boskovic, B.; Zumer, V. Differential evolution for multiobjective optimization with self adaptation. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 3617–3624. [Google Scholar] [CrossRef]
- Reyes-Sierra, M.; Coello, C.A.C. Multi-Objective Particle Swarm Optimizers: A Survey of the State-ofthe-Art. Int. J. Comput. Intell. Res. 2006, 2, 287–308. [Google Scholar]
- Schaffer, J.D. Multiple Objective Optimization with Vector Evaluated Genetic Algorithms. In Proceedings of the First International Conference on Genetic Algorithms and Their Applications; Lawrence Erlbaum Associates Inc.: Hillsdale, NJ, USA, 1985. [Google Scholar]
- Srinivas, N.; Deb, K. Multi-Objective function optimization using non-dominated sorting genetic algorithms. Evol. Comput. 1995, 2, 221–248. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Li, K.; Deb, K.; Zhang, Q.; Kwong, S. An evolutionary manyobjective optimization algorithm based on dominance and decomposition. IEEE Trans. Evol. Comput. 2015, 19, 694–716. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part i: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Li, K.; Wang, R.; Zhang, T.; Ishibuchi, H. Evolutionary many-objective optimization: A comparative study of the state-of-the-art. IEEE Access 2018, 6, 26194–26214. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- While, L.; Hingston, P.; Barone, L.; Huband, S. A faster algorithm for calculating hypervolume. IEEE Trans. Evol. Comput. 2006, 10, 29–38. [Google Scholar] [CrossRef] [Green Version]
- Coello, C.A.C.; Sierra, M.R. A study of the parallelization of a coevolutionary multi-objective evolutionary algorithm. In MICAI 2004: Advances in Artificial Intelligence; Lecture Notes in Computer Science 2972; Springer: Berlin/Heidelberg, Germany, 2004; pp. 688–697. [Google Scholar]
- Ishibuchi, H.; Hiroyuki, M.; Yusuke, N. Pareto Fronts of Many-Objective Degenerate Test Problems. IEEE Trans. Evol. Comput. 2016, 20, 807–813. [Google Scholar] [CrossRef]
- Schutze, O.; Esquivel, X.; Lara, A.; Coello, C.A. Using the Averaged Hausdorff Distance as a Performance Measure in Evolutionary Multi-Objective Optimization. IEEE Trans. Evol. Comput. 2012, 16, 504–522. [Google Scholar] [CrossRef]
- Rudolph, G.; Schutze, O.; Grimme, C.; Dominguez-Medina, C.; Trautmann, H. Optimal Averaged Hausdorff Archives for Bi-objective Problems: Theoretical and Numerical Results. Comput. Optim. Appl. 2016, 64, 589–618. [Google Scholar] [CrossRef]
- Smith, E.K.; Weintraub, S. The Constants in the Equation for Atmospheric Refractive Index at Radio Frequencies. Proc. IRE 1953, 41, 1035–1037. [Google Scholar] [CrossRef] [Green Version]
- Sheng, Z.; Fang, H.X. Monitoring of ducting by using a ground-based GPS receiver. Chin. Phys. B 2013, 22, 575–579. [Google Scholar] [CrossRef]
- Balvedi, G.C.; Walter, F. Analysis of GPS signal propagation in tropospheric ducts using numerical methods. In Proceedings of the 11th URSI Commission Open Symposium on Radio Wave Propagation and Remote Sensing, Rio De Janeiro, Brazil, 30 October–2 November 2007. [Google Scholar]
- Zilinskas, A.; Fraga, E.S.; Mackute, A. Data analysis and visualisation for robust multi-criteria process optimisation. Comput. Chem. Eng. 2006, 30, 1061–1071. [Google Scholar] [CrossRef]















| Algorithms | Parameter Settings | Categories |
|---|---|---|
| GrEA | The grid division: div = 45 for 2 objectives, div = 15 for 4 objectives and 6 objectives, and div = 8 for 8 objectives | C4 |
| HypE | The number of sampling points: 10,000 | C2 |
| KnEA | The rate of knee points in population: K = 0.6 for 2 objectives and K = 0.5 for other conditions. | C3 |
| MOEAD | Neighborhood size T: N = 20 | C1 |
| NSGA-II | —— | C1 |
| NSGA-III | —— | C1, C3 |
| Two_Arch2 (abbreviated to Arch2) | The sizes of CA and DA: N; the p for Lp-norm-based distances: 1/M | C5 |
| Problems | Inversion Slope c1 (N-units/m) | Height h1 (m) | Inversion Slope c2 (N-units/m) | Height h2 (m) | Transmitting Frequency (Hz) and Antenna Height (m) |
|---|---|---|---|---|---|
| Bounds | [−0.1, 0] | [50, 150] | [−0.4, 0] | [250, 350] | [1200, 1600], [0, 200] |
| GPS1 | −0.02 | 100 | −0.2 | 300 | (1200,20) |
| GPS2 | −0.02 | 100 | −0.2 | 300 | (1200,20), (1300,20) |
| GPS3 | −0.02 | 100 | −0.2 | 300 | (1300,20), (1300,20), (1400,100) |
| GPS4 | −0.02 | 100 | −0.2 | 300 | (1300,20), (1400,20), (1500,20) |
| GPS5 | −0.02 | 100 | −0.2 | 300 | (1200,20), (1300,20), (1400,20), (1500,20) |
| Problems | M | D | GrEA | HypE | KnEA | MOEAD | NSGA-II | NSGA-III | Two_Arch2 |
|---|---|---|---|---|---|---|---|---|---|
| GPS1 | 2 | 4 | 2.6585 × 10−2 (1.2 × 10−3) | 2.7326 × 10−2 (1.4026 × 10−4) | 2.6453 × 10−2 (1.1 × 10−3) | 2.6211 × 10−2 (5.3499 × 10−4) | 2.7340 × 10−2 (1.6235 × 10−4) | 2.7221 × 10−2 (2.2596 × 10−4) | 2.7145 × 10−2 (2.1758 × 10−4) |
| GPS1 | 2 | 5 | 2.8349 × 10−2 (2.3061 × 10−4) | 2.8137 × 10−2 (3.2871 × 10−4) | 2.8182 × 10−2 (4.4032 × 10−4) | 2.6666 × 10−2 (6.8280 × 10−4) | 2.8408 × 10−2 (2.8335 × 10−4) | 2.8286 × 10−2 (2.1280 × 10−4) | 2.7963 × 10−2 (9.1389 × 10−4) |
| GPS1 | 2 | 6 | 3.0108 × 10−2 (1.6557 × 10−4) | 2.9960 × 10−2 (2.5793 × 10−4) | 3.0153 × 10−2 (3.1700 × 10−4) | 2.8877 × 10−2 (6.2561 × 10−4) | 3.0131 × 10−2 (2.2698 × 10−4) | 3.0079 × 10−2 (2.3681 × 10−4) | 2.9978 × 10−2 (3.5354 × 10−4) |
| GPS2 | 4 | 4 | 1.0899 × 10−2 (1.6894 × 10−5) | 1.1021 × 10−2 (1.6321 × 10−5) | 1.0525 × 10−2 (9.6309 × 10−5) | 1.0438 × 10−2 (3.7097 × 10−5) | 1.1037 × 10−2 (1.4758 × 10−5) | 1.0977 × 10−2 (1.6595 × 10−5) | 1.0838 × 10−2 (2.2630 × 10−5) |
| GPS2 | 4 | 5 | 1.1982 × 10−2 (2.8865 × 10−5) | 1.1200 × 10−2 (2.4873 × 10−5) | 1.2076 × 10−2 (2.2684 × 10−5) | 1.1106 × 10−2 (4.8637 × 10−5) | 1.2039 × 10−2 (2.1192 × 10−5) | 1.1923 × 10−2 (2.7029 × 10−5) | 1.1848 × 10−2 (2.8737 × 10−5) |
| GPS2 | 4 | 6 | 1.3545 × 10−2 (1.2246 × 10−5) | 1.3466 × 10−2 (2.0637 × 10−5) | 1.3482 × 10−2 (2.9862 × 10−5) | 1.2889 × 10−2 (4.0718 × 10−5) | 1.3434 × 10−2 (2.7438 × 10−5) | 1.3444 × 10−2 (2.3390 × 10−5) | 1.3483 × 10−2 (1.3847 × 10−5) |
| GPS3 | 6 | 4 | 9.5495 × 10−6 (3.7230 × 10−7) | 9.4444 × 10−6 (4.3702 × 10−7) | 9.4124 × 10−6 (4.4887 × 10−7) | 9.3182 × 10−6 (5.2555 × 10−7) | 9.5819 × 10−6 (3.6928 × 10−7) | 9.4182 × 10−6 (3.2268 × 10−7) | 9.1581 × 10−6 (6.3368 × 10−7) |
| GPS3 | 6 | 5 | 8.1222 × 10−6 (3.5643 × 10−7) | 8.3087 × 10−6 (2.5313 × 10−7) | 7.2750 × 10−6 (1.5623 × 10−6) | 8.0208 × 10−6 (9.1172 × 10−8) | 8.2473 × 10−6 (1.7443 × 10−7) | 8.2147 × 10−6 (1.4555 × 10−7) | 7.9161 × 10−6 (4.3874 × 10−7) |
| GPS3 | 6 | 6 | 1.2366 × 10−5 (3.7119 × 10−7) | 1.2321 × 10−5 (3.9267 × 10−7) | 1.2389 × 10−5 (2.8948 × 10−7) | 1.1170 × 10−5 (6.4066 × 10−7) | 1.2508 × 10−5 (2.7469 × 10−7) | 1.2483 × 10−5 (1.4860 × 10−7) | 1.2263 × 10−5 (4.1432 × 10−7) |
| GPS4 | 6 | 4 | 1.0766 × 10−5 (4.0376 × 10−7) | 1.0877 × 10−5 (3.7687 × 10−7) | 9.6252 × 10−6 (2.0121 × 10−6) | 8.9592 × 10−6 (1.0565 × 10−6) | 1.0595 × 10−5 (4.5682 × 10−7) | 1.1130 × 10−5 (1.4302 × 10−7) | 1.0066 × 10−5 (8.2339 × 10−7) |
| GPS4 | 6 | 5 | 7.9950 × 10−6 (4.3028 × 10−7) | 8.6230 × 10−6 (2.7246 × 10−7) | 6.3411 × 10−5 (2.0116 × 10−6) | 8.1312 × 10−6 (4.2131 × 10−7) | 8.4375 × 10−6 (2.3223 × 10−7) | 8.4638 × 10−6 (1.3295 × 10−7) | 8.0950 × 10−6 (3.8519 × 10−7) |
| GPS4 | 6 | 6 | 1.3640 × 10−5 (2.9747 × 10−7) | 1.3610 × 10−5 (3.2202 × 10−7) | 1.3367 × 10−5 (1.0586 × 10−6) | 1.2886×10−5 (5.5139 × 10−7) | 1.3668 × 10−5 (3.3885 × 10−7) | 1.3822 × 10−5 (4.2498 × 10−7) | 1.3465 × 10−5 (6.4182 × 10−7) |
| GPS5 | 8 | 4 | 4.5080 × 10−7 (4.2434 × 10−8) | 4.9980 × 10−7 (1.7298 × 10−8) | 3.7706 × 10−7 (1.2623 × 10−7) | 4.4763 × 10−7 (2.0364 × 10−8) | 4.9074 × 10−7 (1.5488 × 10−8) | 4.3703 × 10−7 (6.8565 × 10−8) | 4.6521 × 10−7 (2.9975 × 10−8) |
| GPS5 | 8 | 5 | 6.2653 × 10−7 (5.8938 × 10−8) | 6.636 × 10−7 (5.3241 × 10−8) | 5.7397 × 10−7 (1.3440 × 10−7) | 5.9696 × 10−7 (2.0599 × 10−8) | 6.4617 × 10−7 (4.7842 × 10−8) | 6.5795 × 10−7 (2.4359 × 10−8) | 5.9994 × 10−7 (5.2125 × 10−8) |
| GPS5 | 8 | 6 | 8.9834 × 10−7 (2.7039 × 10−8) | 8.8444 × 10−7 (3.1179 × 10−8) | 8.9006 × 10−7 (3.9642 × 10−8) | 9.1153 × 10−7 (2.2031 × 10−9) | 8.9607 × 10−7 (2.8872 × 10−8) | 9.0699 × 10−7 (2.2425 × 10−8) | 8.6747 × 10−7 (4.7054 × 10−8) |
| Problems | M | D | GrEA | HypE | KnEA | MOEAD | NSGA-II | NSGA-III | Two_Arch2 |
|---|---|---|---|---|---|---|---|---|---|
| GPS1 | 2 | 4 | 0.5532 (0.1249) | 0.6959 (0.1768) | 0.5667 (0.1090) | 0.6142 (0.1200) | 0.5644 (0.1489) | 0.5406 (0.1580) | 0.6288 (0.1513) |
| GPS1 | 2 | 5 | 0.5247 (0.1210) | 0.6760 (0.1905) | 0.5690 (0.1300) | 0.6518 (0.1473) | 0.5228 (0.1058) | 0.5314 (0.1253) | 0.5318 (0.0878) |
| GPS1 | 2 | 6 | 0.5031 (0.1238) | 0.4727 (0.0872) | 0.4978 (0.0707) | 0.6805 (0.1607) | 0.4279 (0.0714) | 0.4305 (0.0915) | 0.4879 (0.0679) |
| GPS2 | 4 | 4 | 0.5624 (0.1260) | 0.6459 (0.1151) | 0.6535 (0.1688) | 0.8319 (0.1605) | 0.4927 (0.0657) | 0.5685 (0.1145) | 0.6069 (0.1652) |
| GPS2 | 4 | 5 | 0.6610 (0.1435) | 0.8141 (0.2557) | 0.7091 (0.1587) | 0.8317 (0.1570) | 0.6615 (0.1898) | 0.6568 (0.1616) | 0.6876 (0.1553) |
| GPS2 | 4 | 6 | 0.6638 (0.2484) | 0.7159 (0.1517) | 0.6581 (0.1344) | 0.8238 (0.1888) | 0.6289 (0.1137) | 0.6469 (0.1965) | 0.6553 (0.1374) |
| GPS3 | 6 | 4 | 0.7549 (0.2221) | 1.1262 (0.3770) | 0.7968 (0.2498) | 0.6521 (0.0750) | 0.7781 (0.2516) | 0.7835 (0.2078) | 0.9112 (0.2722) |
| GPS3 | 6 | 5 | 0.7158 (0.2150) | 1.0103 (0.3764) | 0.7243 (0.1344) | 0.5938 (0.0489) | 0.7121 (0.2816) | 0.6588 (0.0937) | 0.7306 (0.1435) |
| GPS3 | 6 | 6 | 0.5558 (0.0609) | 0.6736 (0.1674) | 0.7556 (0.1466) | 0.7643 (0.1450) | 0.5958 (0.1791) | 0.7020 (0.1076) | 0.6620 (0.1680) |
| GPS4 | 6 | 4 | 0.7356 (0.2319) | 0.9056 (0.2345) | 0.8331 (0.2543) | 0.6157 (0.0396) | 0.7662 (0.2418) | 0.8304 (0.2317) | 0.8278 (0.2028) |
| GPS4 | 6 | 5 | 0.6563 (0.1441) | 0.6673 (0.1811) | 0.8381 (0.2543) | 0.6636 (0.0618) | 0.7548 (0.1819) | 0.7102 (0.1016) | 0.7586 (0.2310) |
| GPS4 | 6 | 6 | 2.5250 (0.3814) | 1.6106 (0.3036) | 2.6256 (0.4999) | 2.2671 (0.1551) | 2.5251 (0.4160) | 2.3696 (0.3275) | 2.4804 (0.4206) |
| GPS5 | 8 | 4 | 0.6806 (0.0966) | 0.8271 (0.2138) | 1.0168 (0.3198) | 0.9126 (0.1148) | 0.6615 (0.0663) | 0.7255 (0.0993) | 0.6372 (0.1070) |
| GPS5 | 8 | 5 | 0.8639 (0.3150) | 1.1382 (0.2753) | 0.9790 (0.2757) | 0.9684 (0.2279) | 0.7955 (0.1982) | 0.7811 (0.0913) | 0.8788 (0.1610) |
| GPS5 | 8 | 6 | 0.8459 (0.1712) | 1.1966 (0.3723) | 1.0193 (0.3186) | 0.7708 (0.1000) | 0.7309 (0.1509) | 0.8055 (0.1254) | 0.8549 (0.2116) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, Q.; Sheng, Z.; Shi, H.; Zhang, L.; Zhou, L.; Ge, W.; Long, Z. A Comparative Study on Evolutionary Multi-objective Optimization Algorithms Estimating Surface Duct. Sensors 2018, 18, 4428. https://doi.org/10.3390/s18124428
Liao Q, Sheng Z, Shi H, Zhang L, Zhou L, Ge W, Long Z. A Comparative Study on Evolutionary Multi-objective Optimization Algorithms Estimating Surface Duct. Sensors. 2018; 18(12):4428. https://doi.org/10.3390/s18124428
Chicago/Turabian StyleLiao, Qixiang, Zheng Sheng, Hanqing Shi, Lei Zhang, Lesong Zhou, Wei Ge, and Zhiyong Long. 2018. "A Comparative Study on Evolutionary Multi-objective Optimization Algorithms Estimating Surface Duct" Sensors 18, no. 12: 4428. https://doi.org/10.3390/s18124428
APA StyleLiao, Q., Sheng, Z., Shi, H., Zhang, L., Zhou, L., Ge, W., & Long, Z. (2018). A Comparative Study on Evolutionary Multi-objective Optimization Algorithms Estimating Surface Duct. Sensors, 18(12), 4428. https://doi.org/10.3390/s18124428





