Coil Inductance Model Based Solenoid on–off Valve Spool Displacement Sensing via Laser Calibration
Abstract
:1. Introduction
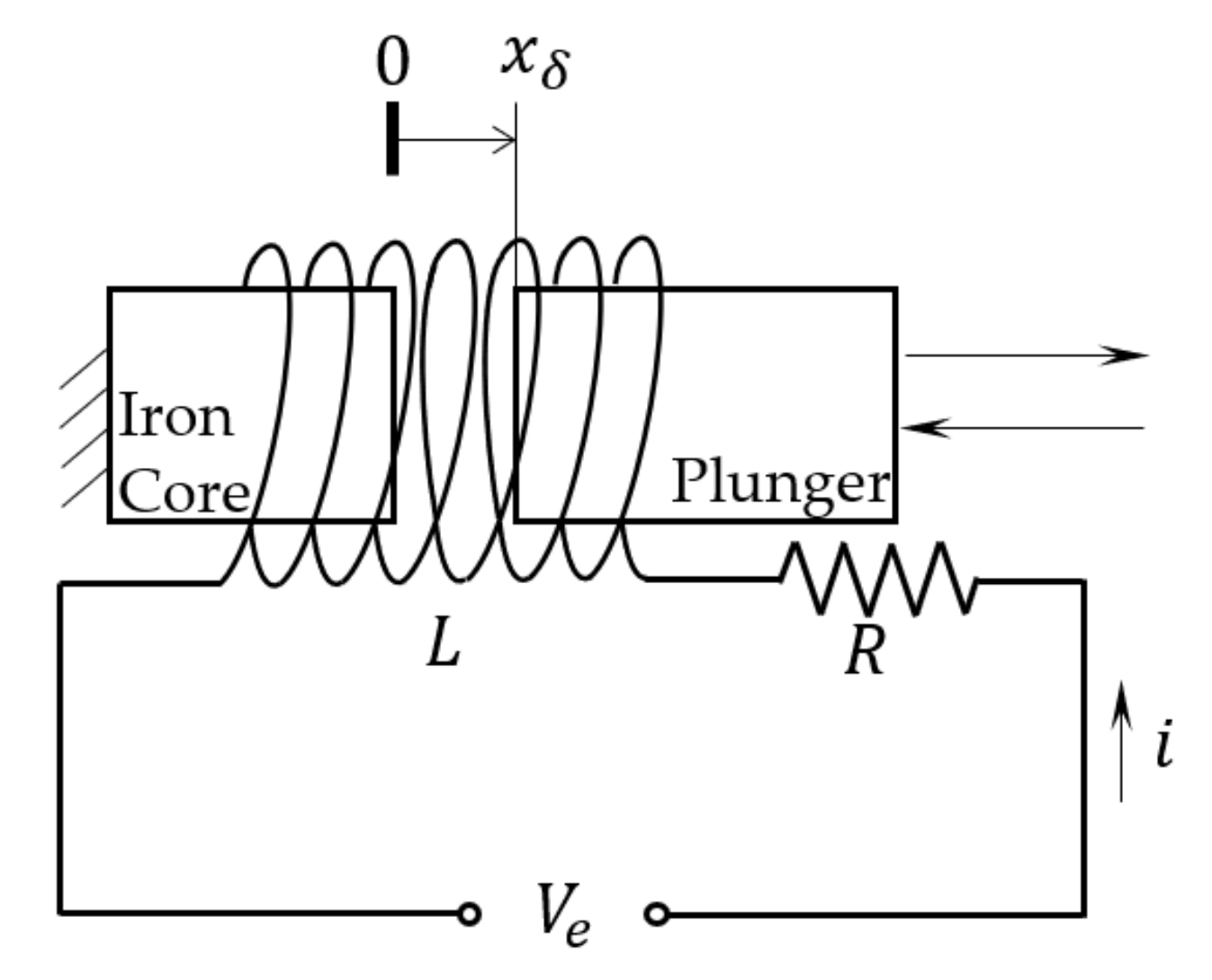
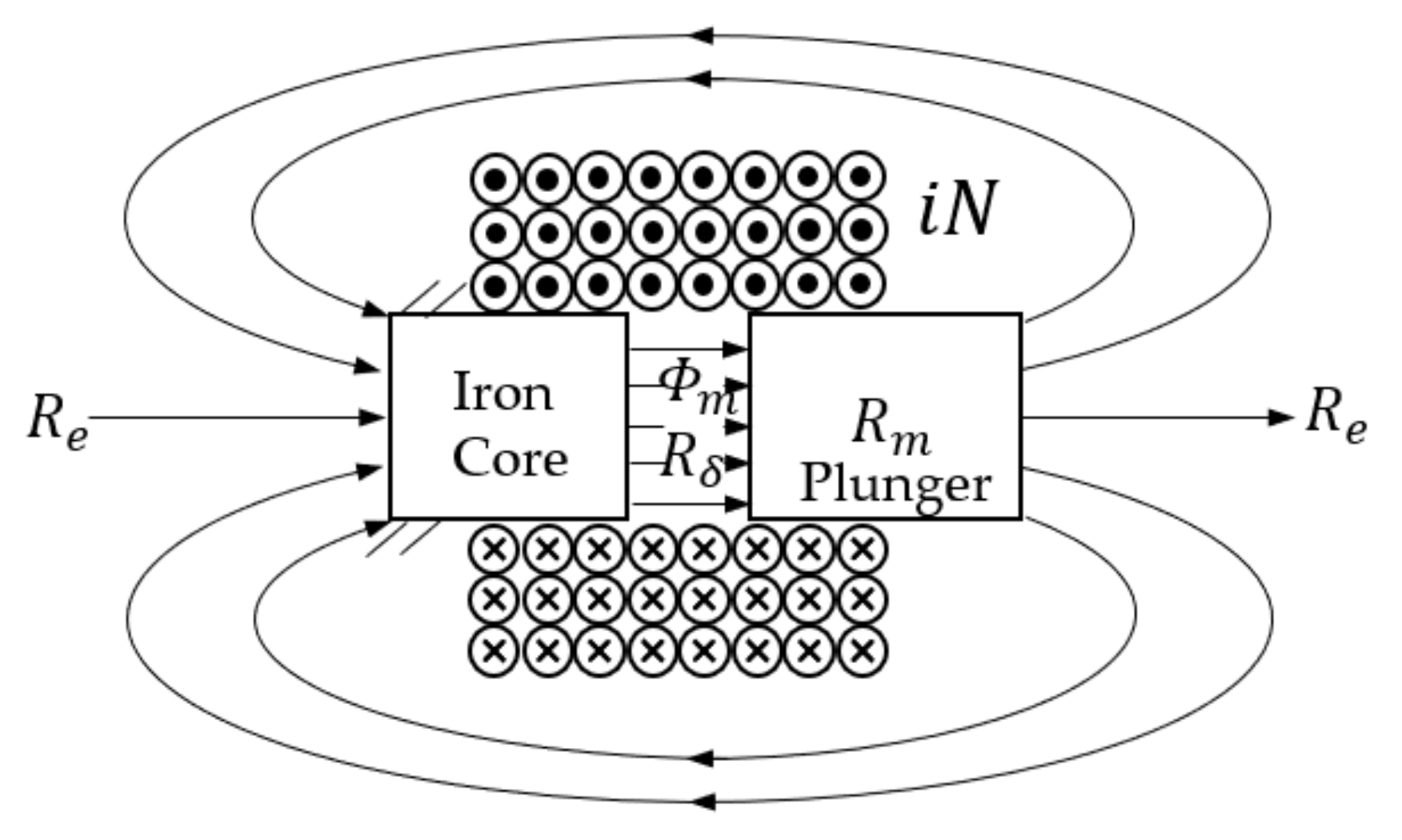
2. On–off Solenoid Electromagnetic Model
2.1. Electromagnetic Model
2.2. Spool Displacement Function
2.3. Numerical Solution Methods
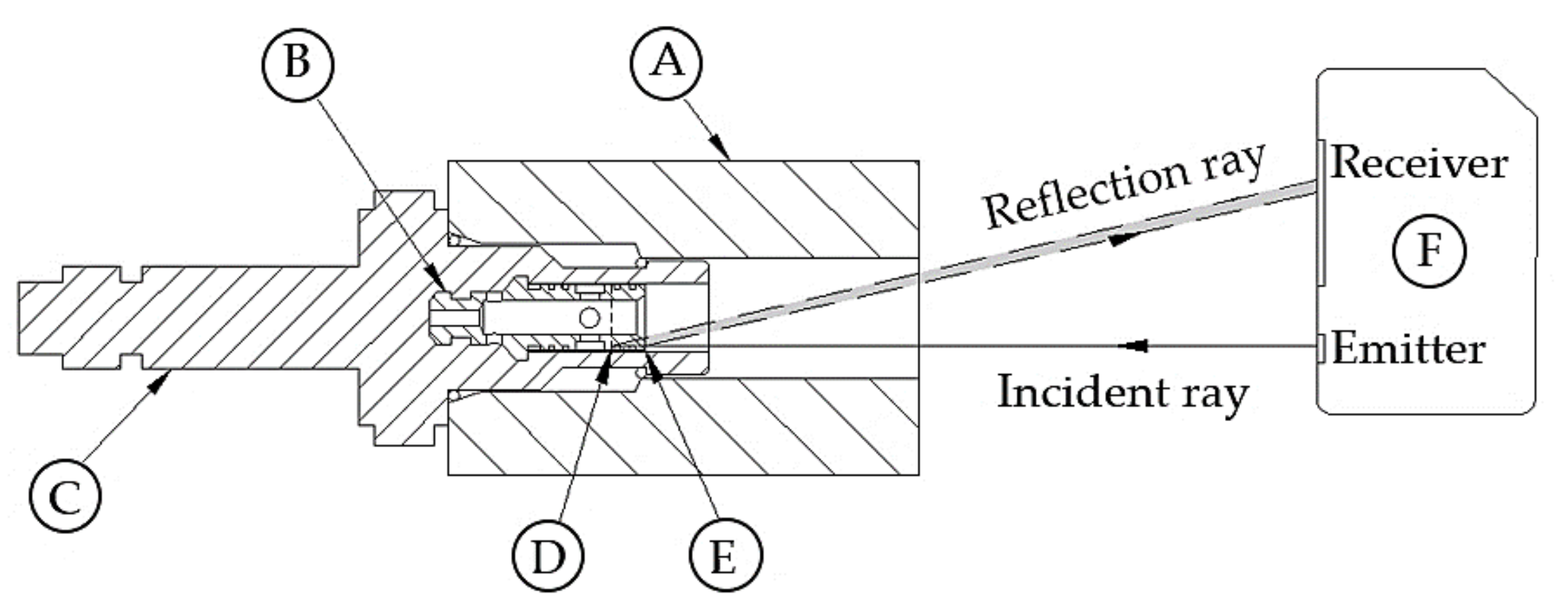
3. Experiment Design
3.1. Optical Measurement Principle
3.2. Testbed
3.3. Dynamic Test Procedures
4. Results and Discussions
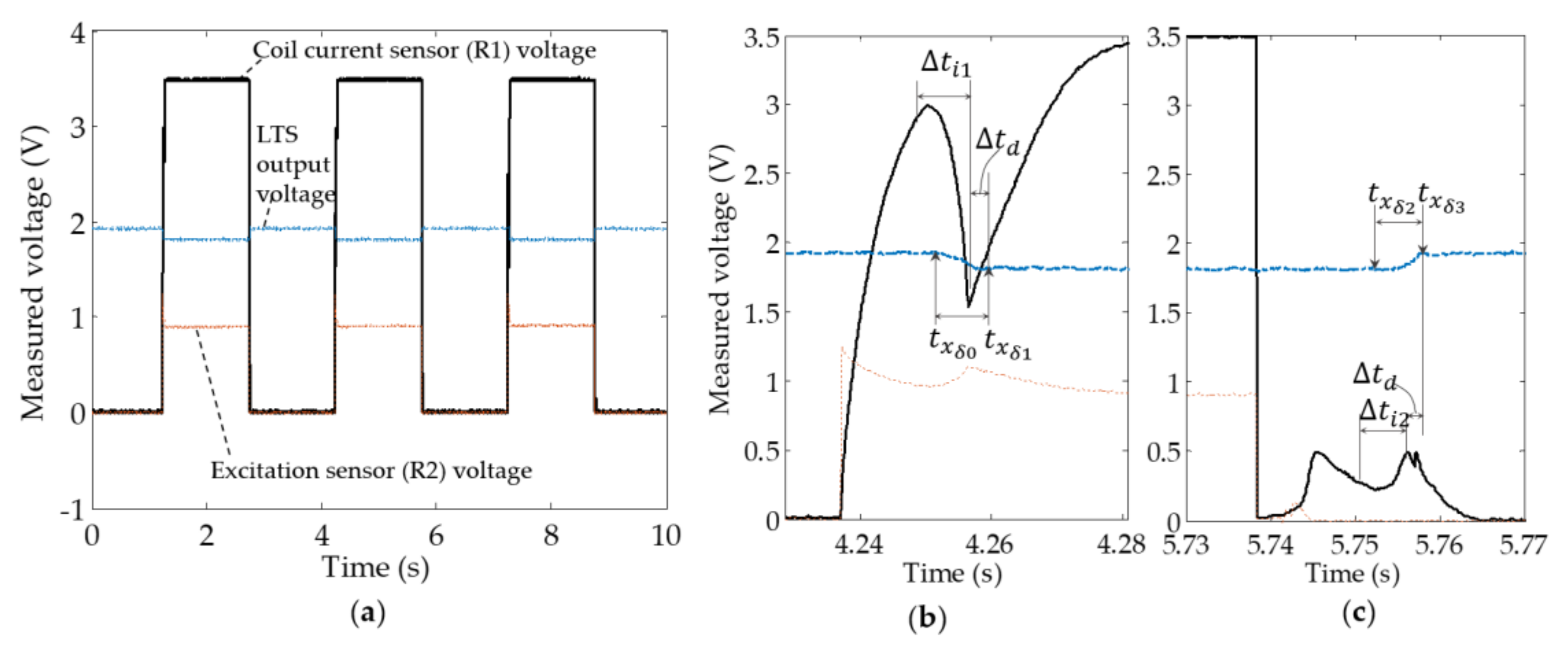
4.1. Data Acquisition and Preprocess
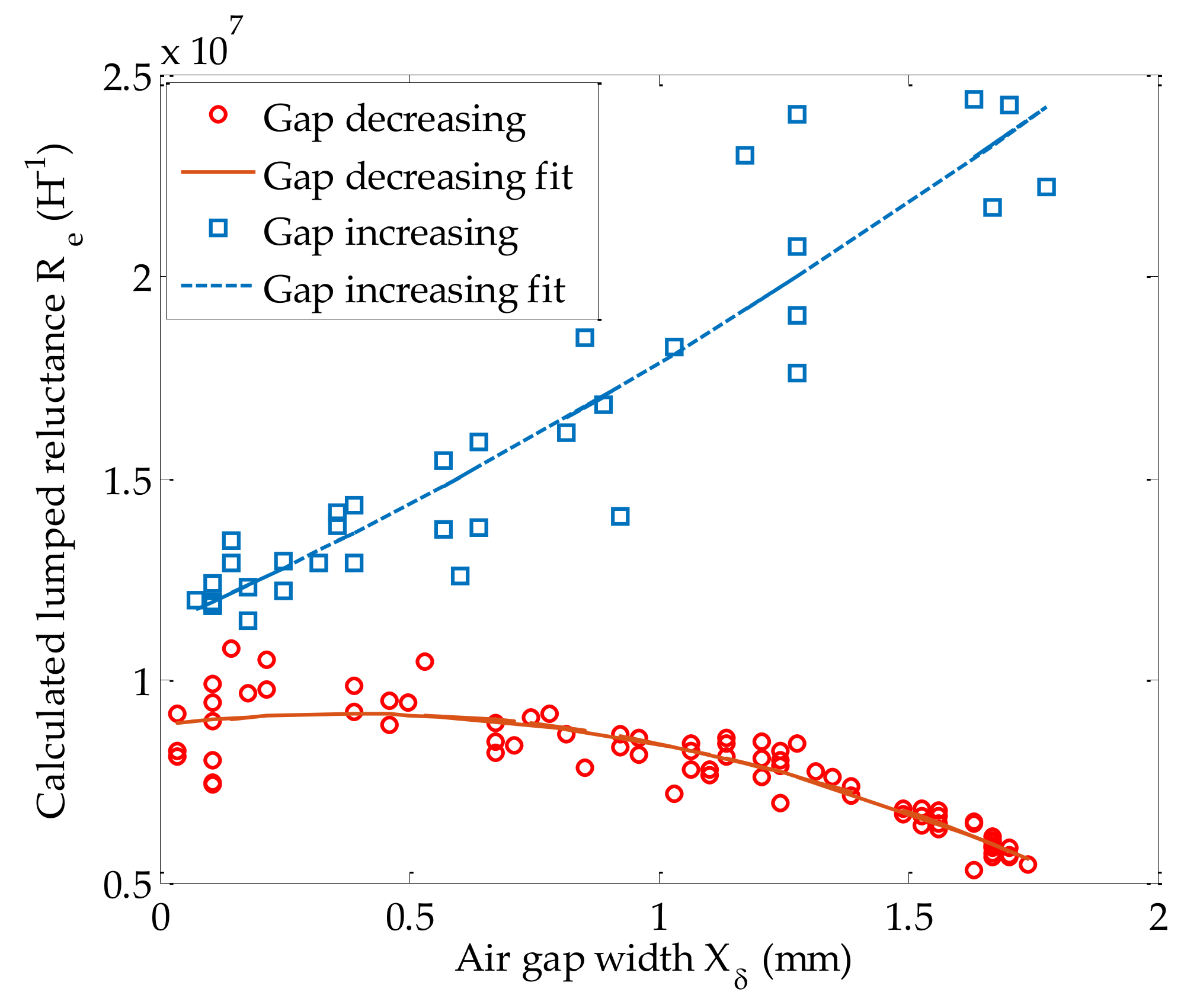
4.2. Calculation of
4.3. Determination of
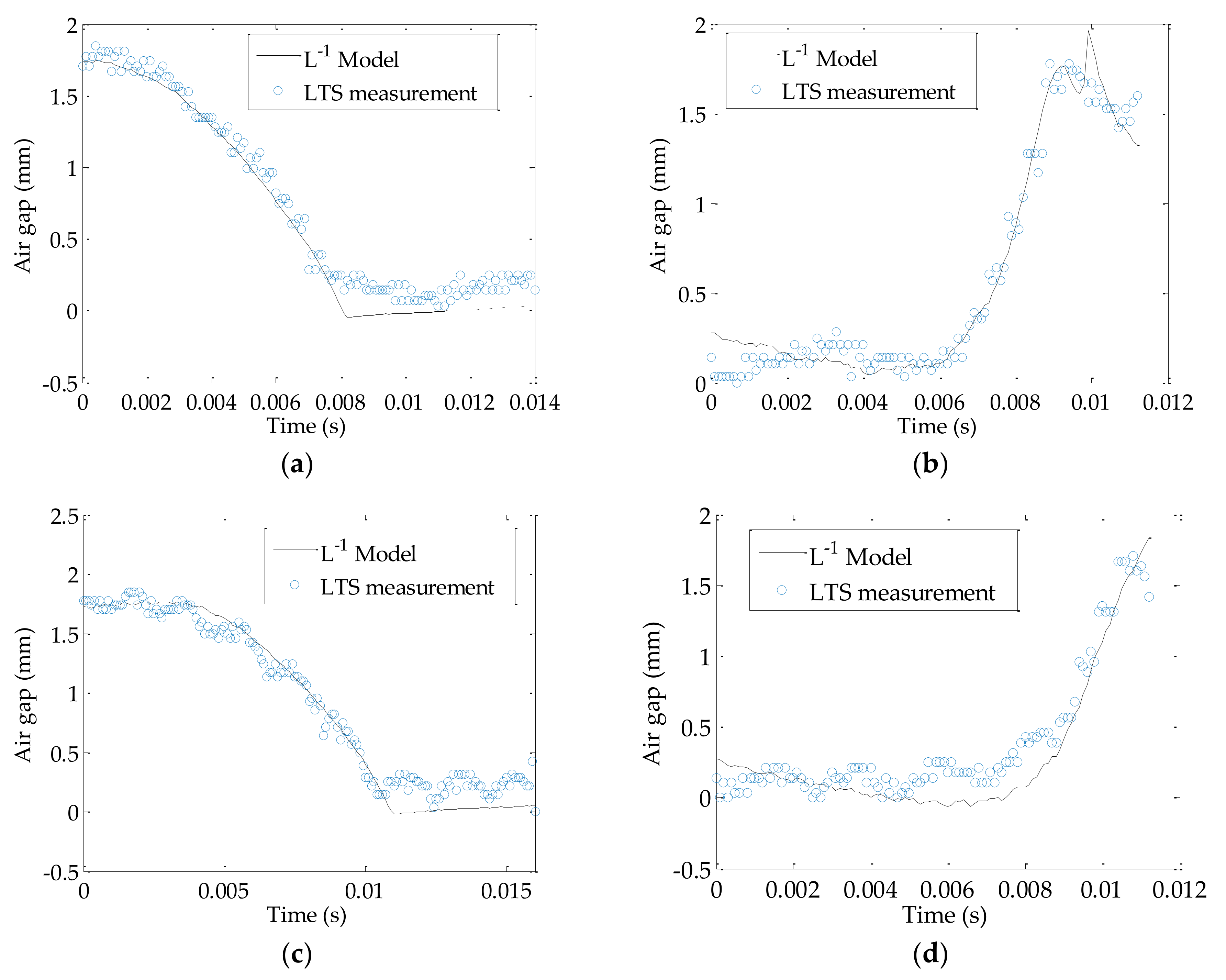
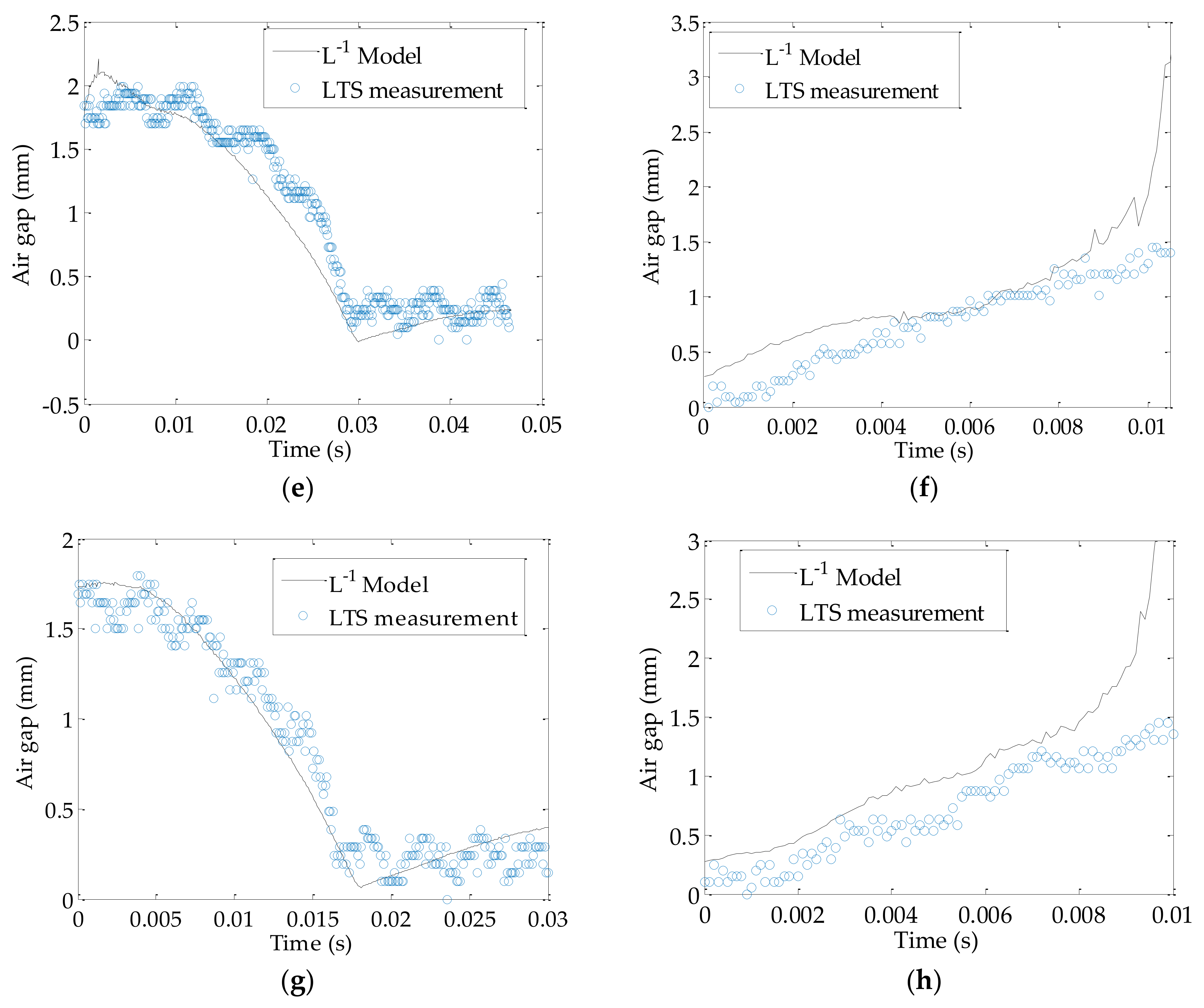
4.4. Performance of Inductance Model
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Convergence Study

References
- Direct Drive Digital Control Servo Valves. Available online: www.moog.com/literature/ICD/Moog-ServoValves-D638_D639-Catalog-en.pdf (accessed on 1 October 2018).
- Direct Operated Proportional DC Valve with Position Feedback. Available online: www.parker.cz/wp-content/uploads/2017/01/HY11-3360UK-D_FC.pdf (accessed on 1 October 2018).
- Tu, H.C.; Rannow, M.B.; Van de Ven, J.D.; Wang, M.; Li, P.Y.; Chase, T.R. High Speed Rotary Pulse Width Modulated On/Off Valve. In Proceedings of the 2007 ASME-IMECE, Seattle, WA, USA, 11–15 November 2007. [Google Scholar]
- Mahrenholz, J.; Lumkes, J. Analytical coupled modeling and model validation of hydraulic on/off valves. J. Dyn. Syst. Meas. Control 2010, 1, 011005. [Google Scholar] [CrossRef]
- Holland, M.A. Design of Digital Pump/Motors and Experimental Validation of Operating Strategies. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2012. [Google Scholar]
- Rømer, D.B.; Johansen, P.; Pedersen, H.C.; Andersen, T.O. Analysis of Dynamic Properties of a Fast Switching On-Off Valve for Digital Displacement Pumps. In Proceedings of the Fluid Power and Motion Control, Barth, UK, 12–14 September 2012. [Google Scholar]
- Winkler, B.; Ploeckinger, A.; Scheidl, R. A novel piloted fast switching multi poppet valve. Int. J. Fluid Power 2010, 3, 7–14. [Google Scholar] [CrossRef]
- Knutson, A.; Van de Ven, J. Modelling and experimental validation of the displacement of a check valve in a hydraulic piston pump. Int. J. Fluid Power 2016, 17, 114–124. [Google Scholar] [CrossRef]
- Vaughan, N.D.; Gamble, J.B. The modeling and simulation of a proportional solenoid valve. J. Dyn. Syst. Meas. Control 1996, 118, 120–125. [Google Scholar] [CrossRef]
- Yudell, A.; Van de Ven, J. Predicting solenoid valve spool displacement through current analysis. Int. J. Fluid Power 2015, 16, 133–140. [Google Scholar] [CrossRef]
- Lee, J.H.; Yun, Y.W.; Hong, H.W.; Park, M.K. Control of spool position of on/off solenoid operated hydraulic valve by sliding-mode controller. J. Mech. Sci. Technol. 2015, 29, 5395–5408. [Google Scholar] [CrossRef]
- Eyabi, P.; Washington, G. Modeling and sensorless control of an electromagnetic valve actuator. Mechatronics 2006, 16, 159–175. [Google Scholar] [CrossRef]
- Glück, T.; Kemmetmüller, W.; Tump, C.; Kugi, A. A novel robust position estimator for self-sensing magnetic levitation systems based on least squares identification. Control Eng. Pract. 2011, 19, 146–157. [Google Scholar] [CrossRef]
- Braun, T.; Reuter, J.; Rudolph, J. Position observation for proportional solenoid valves by signal injection. IFAC-Pap. 2016, 49, 74–79. [Google Scholar] [CrossRef]
- Braun, T.; Reuter, J.; Rudolph, J. A novel observer approach for self sensing of single-coil digital valves. IFAC-Pap. 2017, 50, 782–787. [Google Scholar] [CrossRef]
- Wu, S.; Zhao, X.; Li, C.; Jiao, Z.X.; Qu, F. Multiobjective optimization of a hollow plunger type solenoid for high speed on/off valve. IEEE Trans. Ind. Electron. 2018, 65, 3115–3124. [Google Scholar] [CrossRef]
- Dülk, I.; Kovácsházy, T. A Sensorless method for detecting spool position in solenoid actuators. Carpathian J. Electron. Comput. Eng. 2013, 6, 36–43. [Google Scholar] [CrossRef]
- Nagai, S.; Nozaki, T.; Kawamura, A. Environmental robust position control for compact solenoid actuators by sensorless simultaneous estimation of position and force. IEEE Trans. Ind. Electron. 2016, 63, 5078–5086. [Google Scholar] [CrossRef]
- SV08-25. Available online: https://www.hydraforce.com/Solenoid/Sol-pdf/1-070-1.pdf (accessed on 1 October 2018).
- Zhao, X.; Li, L.; Song, J.; Li, C.; Gao, X. Linear control of switching valve in vehicle hydraulic control unit based on sensorless solenoid position estimation. IEEE Trans. Ind. Electron. 2016, 63, 4073–4085. [Google Scholar] [CrossRef]




| Measurement Range (mm) | Linearity (%) | Laser Wavelength (nm) | Beam Diameter (μm) | Response Frequency (kHz) |
|---|---|---|---|---|
| 100 ± 35 | ±0.1 | 655 | 120 | 0.66 |
| Coil Turns | Magnetic Permeability of Air (H/m) | Plunger Outer Diameter (mm) | Air Gap Area (mm2) | Maximum Air Gap Width (mm) | Coil Electrical Resistance (Ω) |
|---|---|---|---|---|---|
| 2259 | 4π 10−7 | 11.18 | 88.39 | 1.7 | 36.67 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, H.; Zhao, Y. Coil Inductance Model Based Solenoid on–off Valve Spool Displacement Sensing via Laser Calibration. Sensors 2018, 18, 4492. https://doi.org/10.3390/s18124492
Tian H, Zhao Y. Coil Inductance Model Based Solenoid on–off Valve Spool Displacement Sensing via Laser Calibration. Sensors. 2018; 18(12):4492. https://doi.org/10.3390/s18124492
Chicago/Turabian StyleTian, Hao, and Yuren Zhao. 2018. "Coil Inductance Model Based Solenoid on–off Valve Spool Displacement Sensing via Laser Calibration" Sensors 18, no. 12: 4492. https://doi.org/10.3390/s18124492
APA StyleTian, H., & Zhao, Y. (2018). Coil Inductance Model Based Solenoid on–off Valve Spool Displacement Sensing via Laser Calibration. Sensors, 18(12), 4492. https://doi.org/10.3390/s18124492





