A Novel Beamforming Algorithm for GNSS Receivers with Dual-Polarized Sensitive Arrays in the Joint Space–Time-Polarization Domain
Abstract
:1. Introduction
2. Mathematical Model
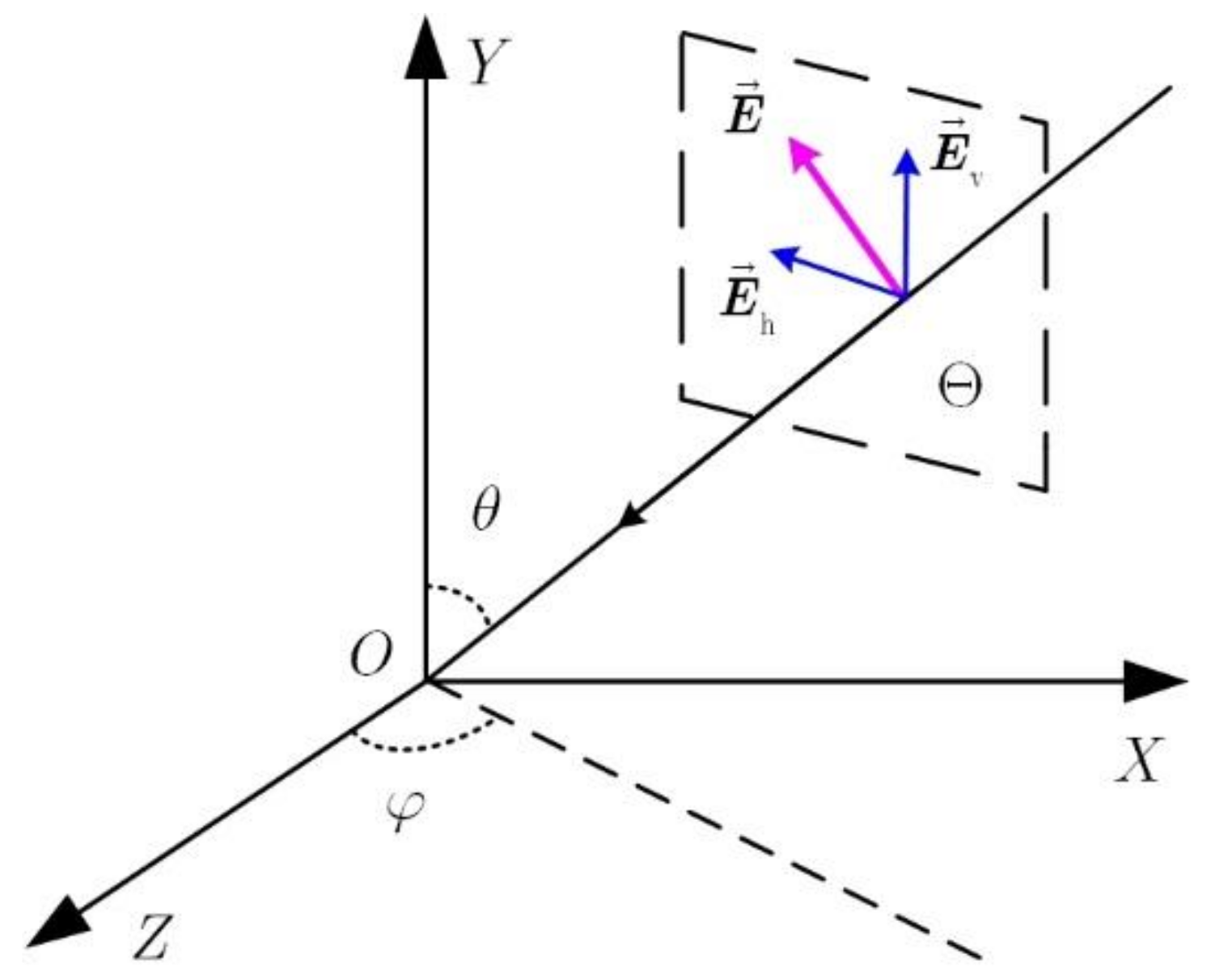
2.1. Polarization Mode
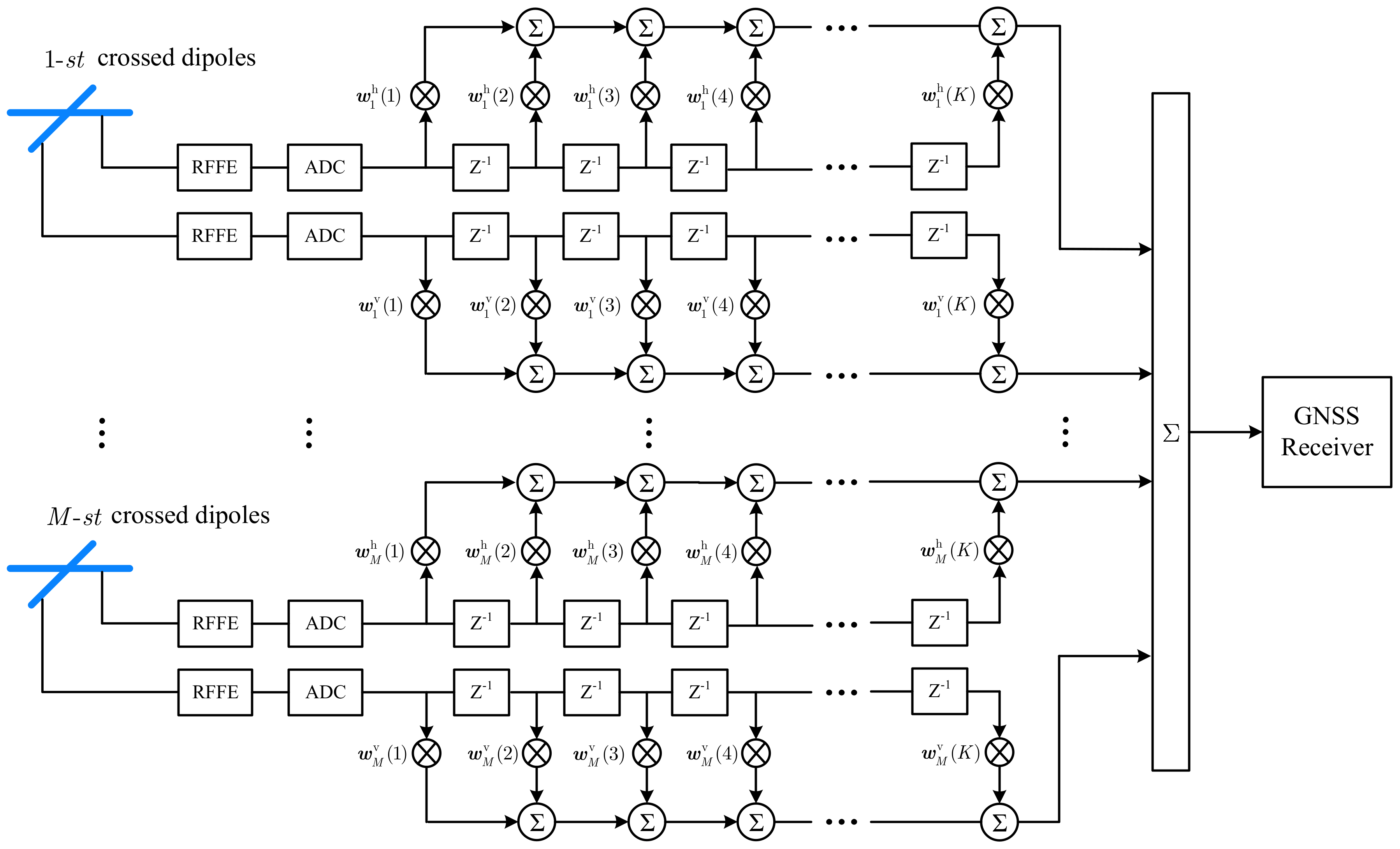
2.2. STPAP Architechture
3. Proposed STPAP Beamforming Algorithm
3.1. Novel MVDR-Based Criterion
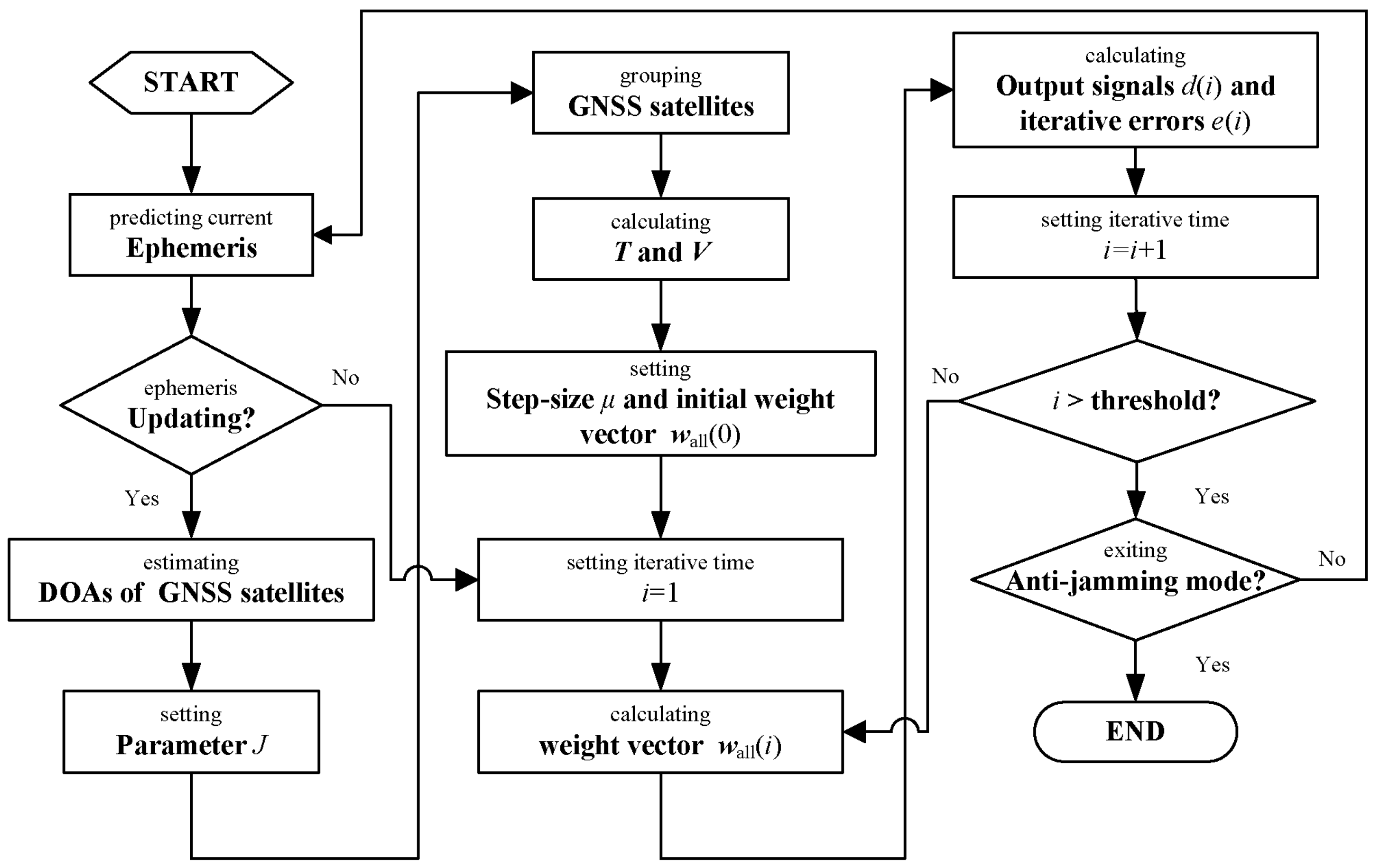
3.2. Adaptive Algorithm for Calculating the Weight Vector
4. Simulation Results
4.1. Effectiveness Validation of the Proposed STPAP Beamforming Algorithm
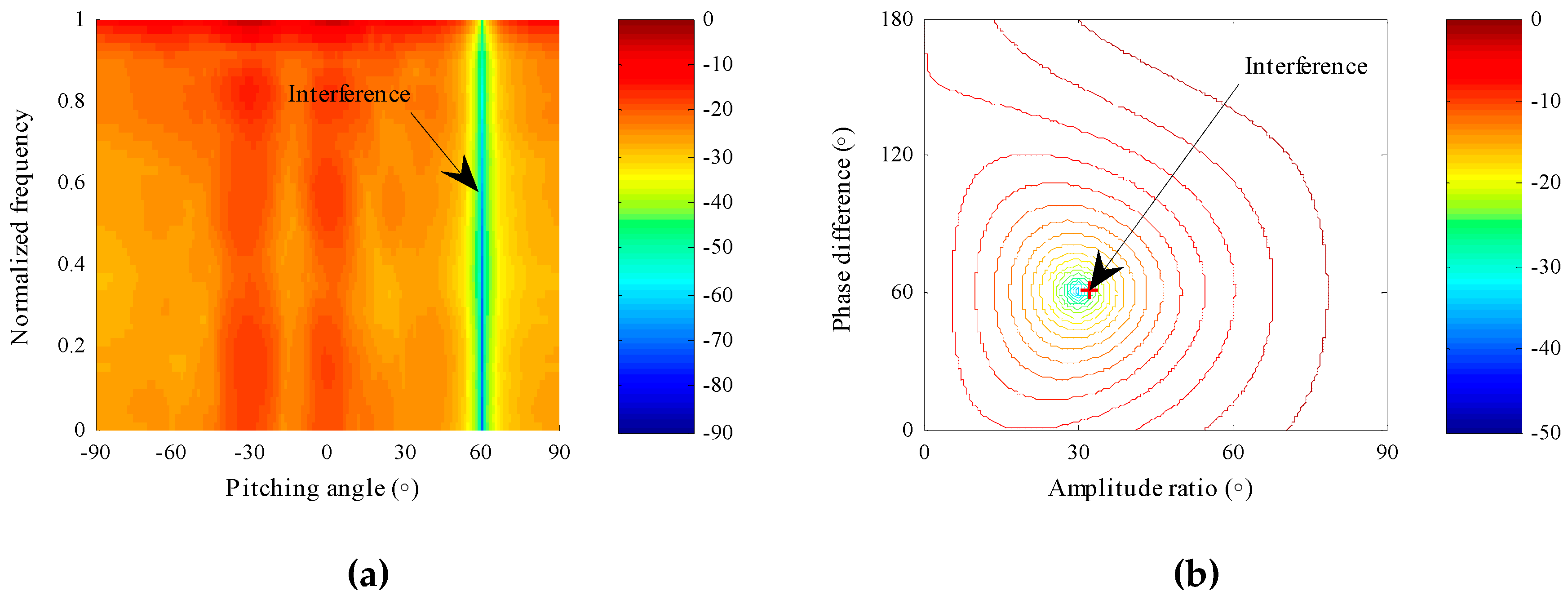
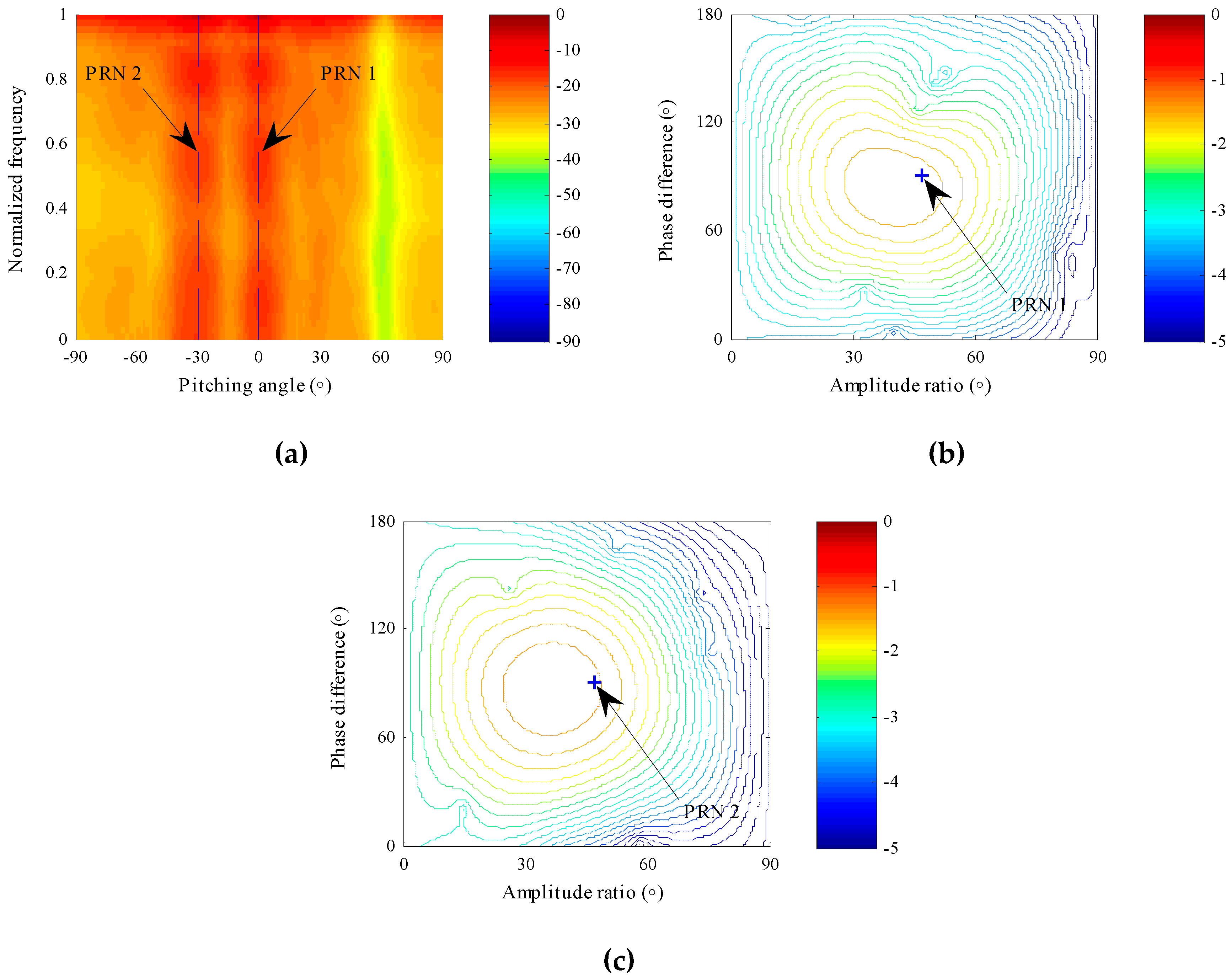
4.1.1. Array Pattern in the Joint Space–Time-Polarization Domain
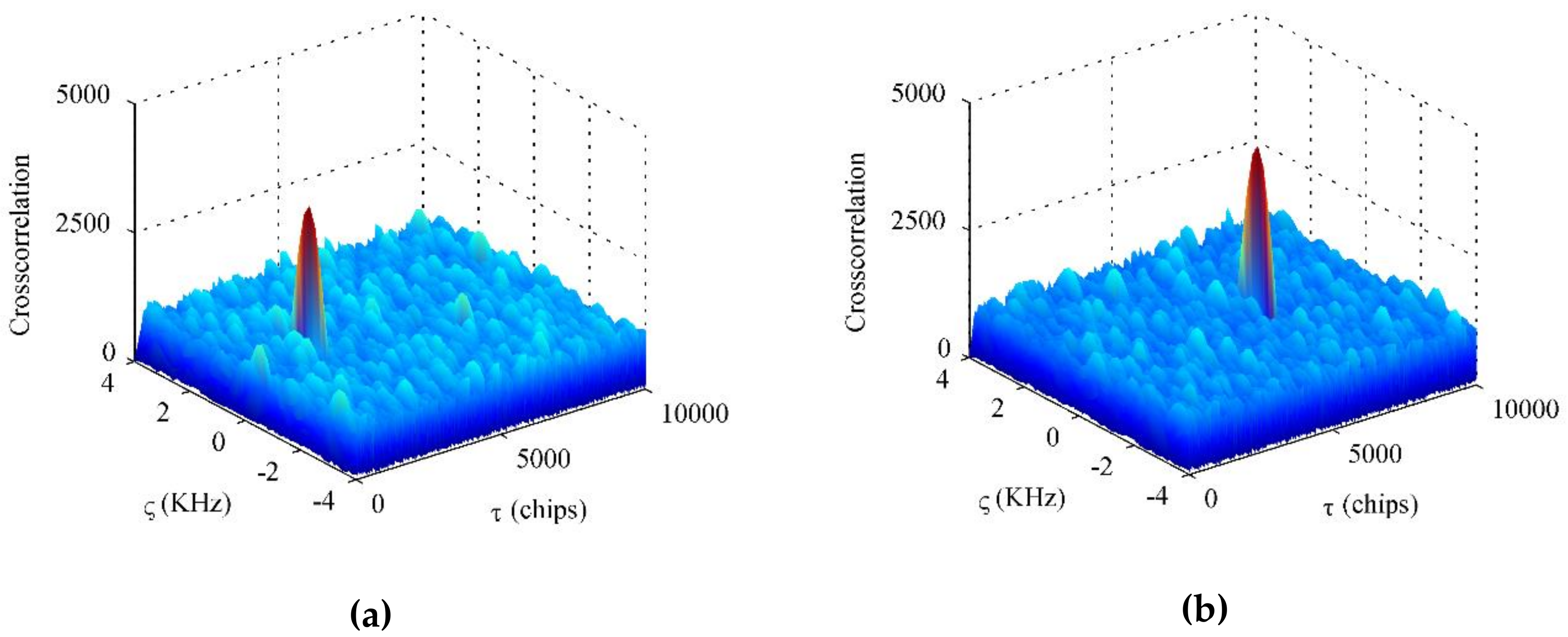
4.1.2. Signal Acquisition in the BD2 Software Receiver
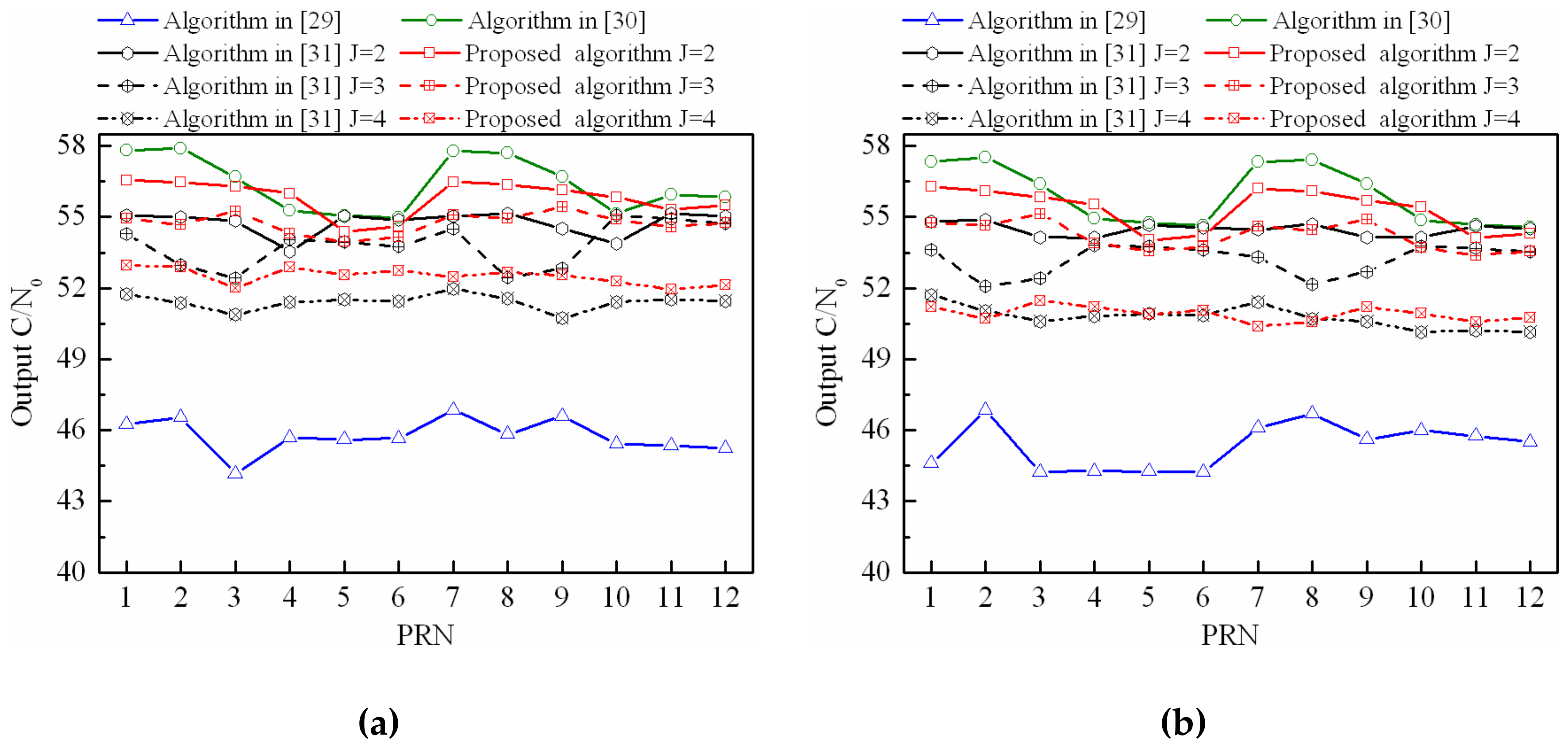
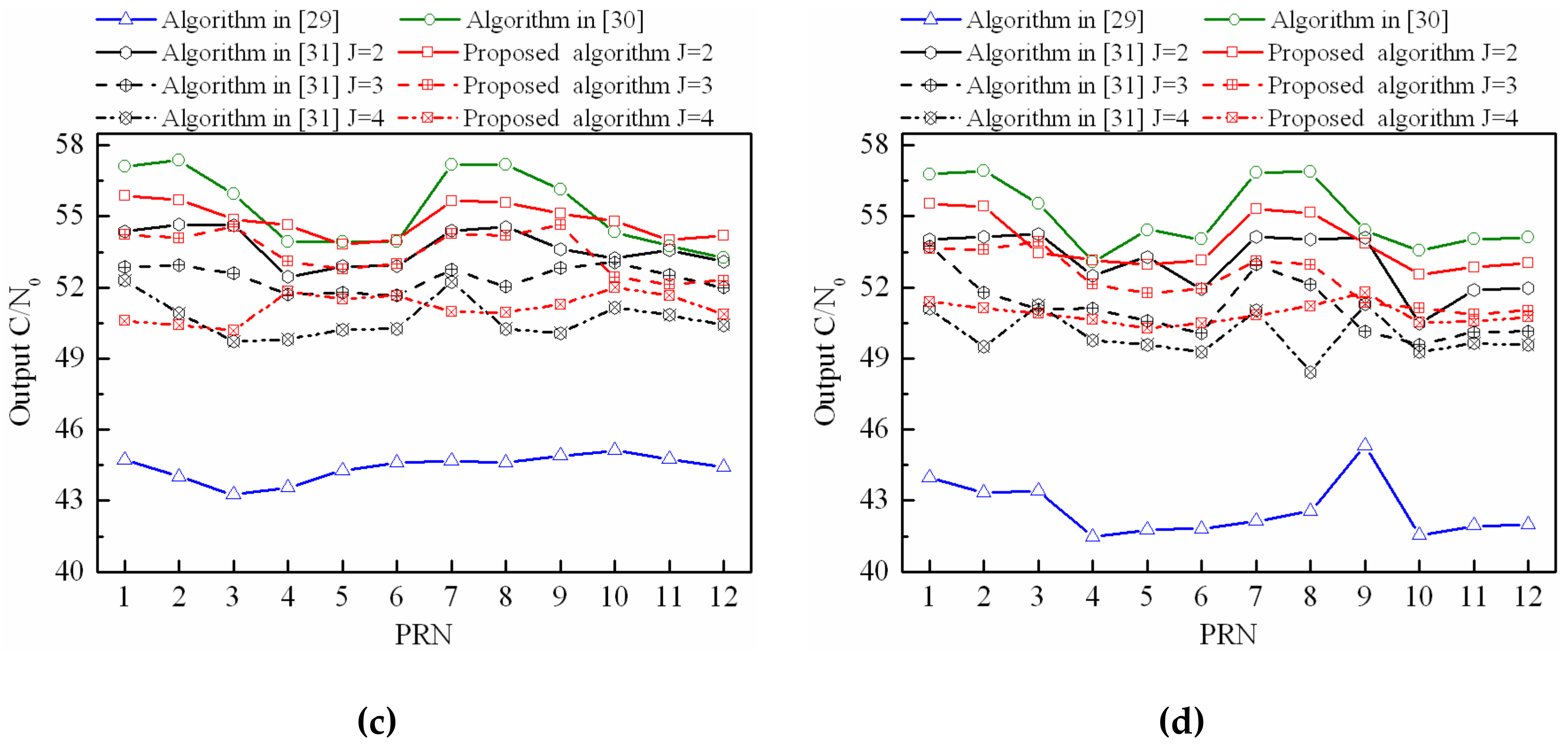
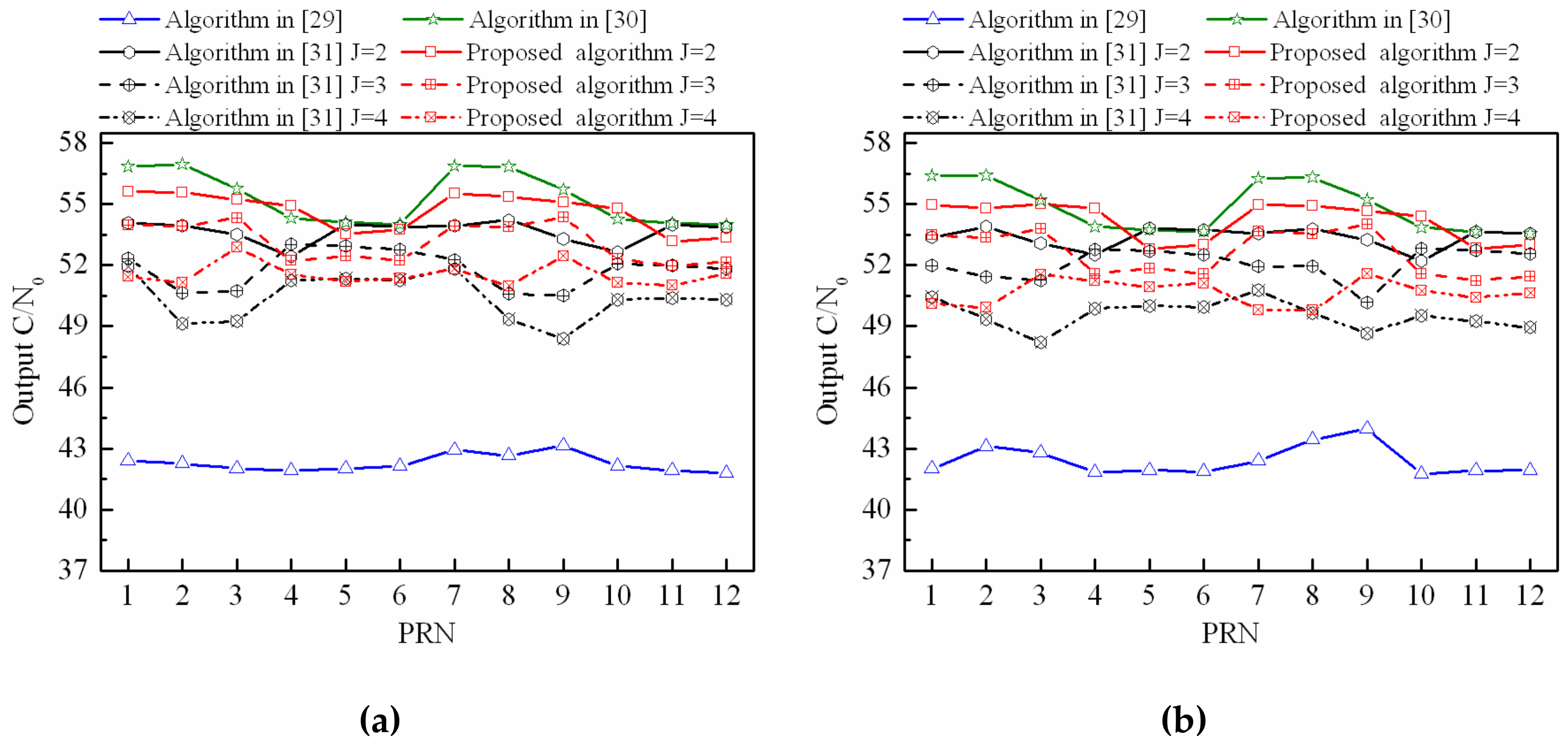
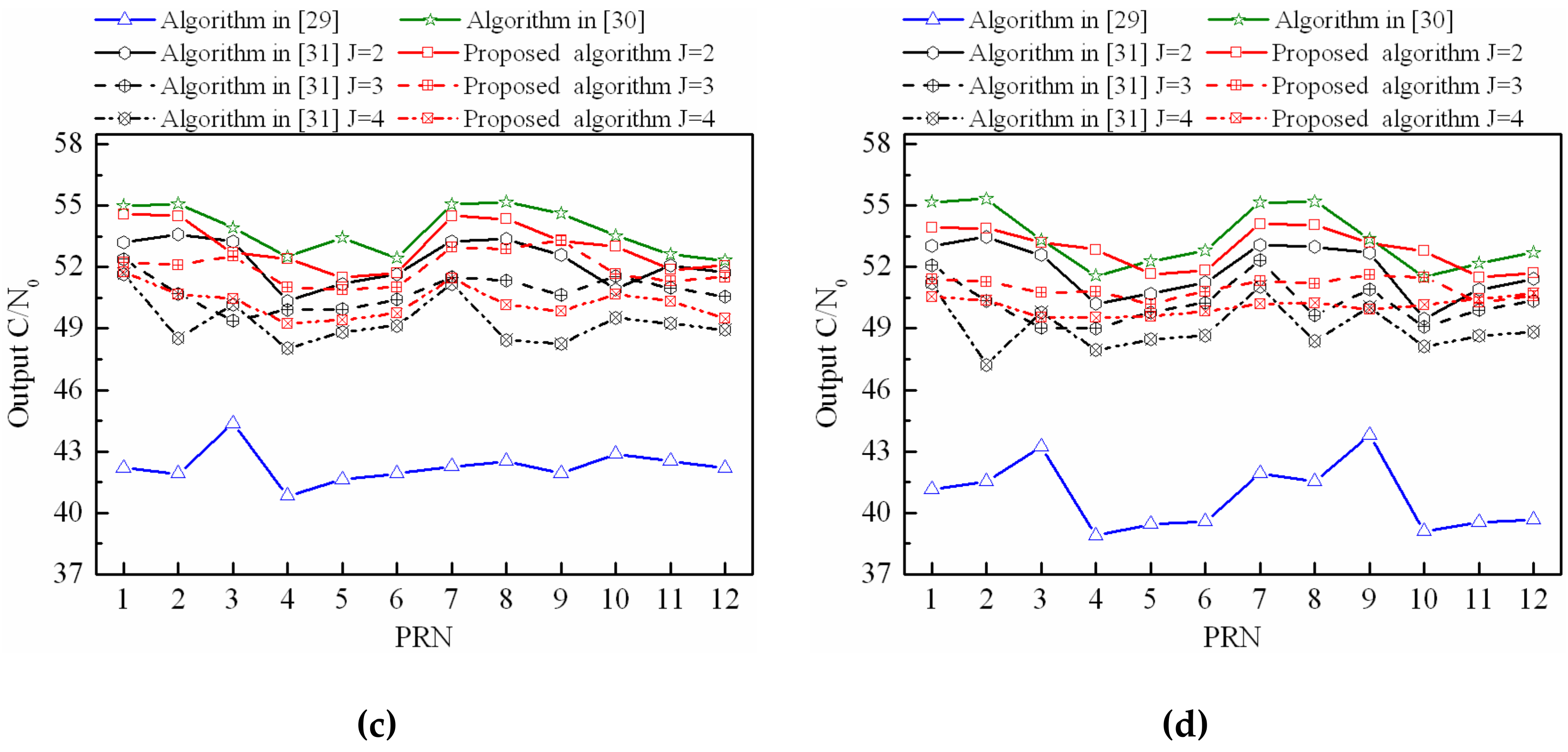
4.2. Output C/N0 Performance when Interferences with Different Polarization Modes
4.3. Output C/N0 Performance When Interferences with the Same Polarization Mode
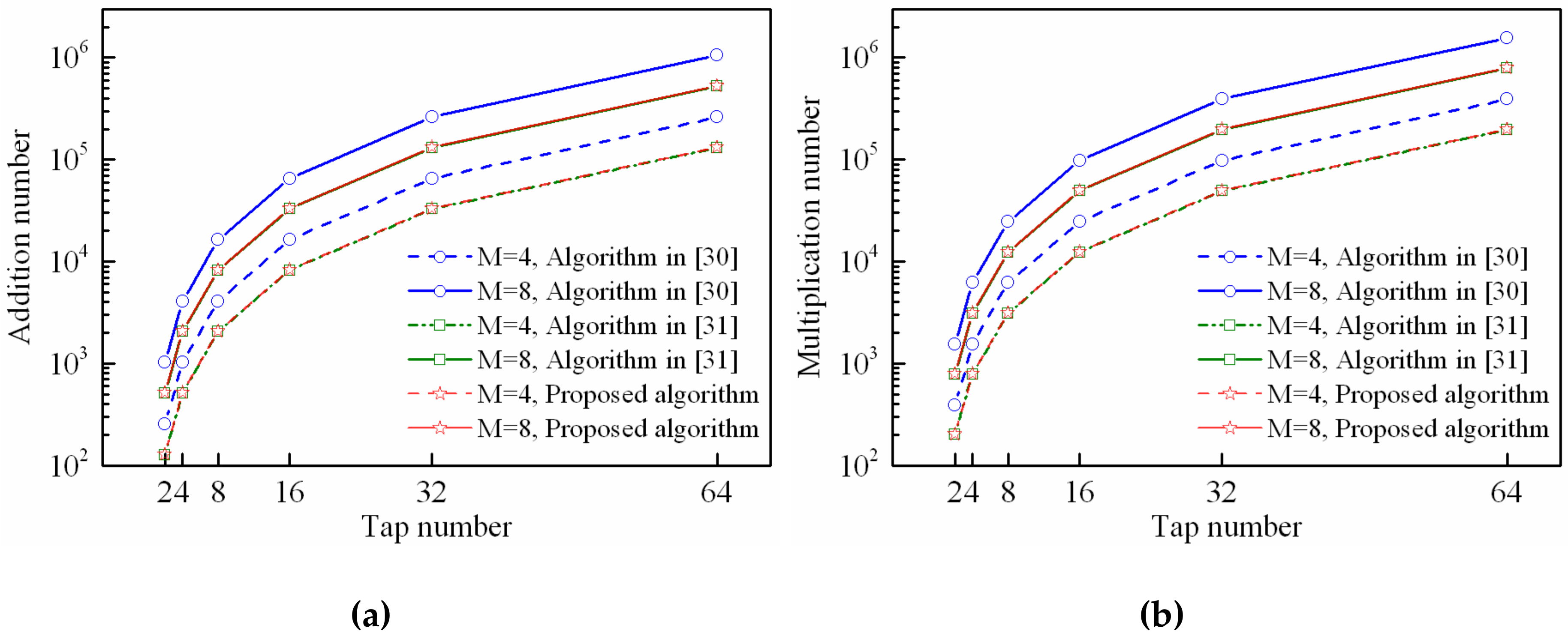
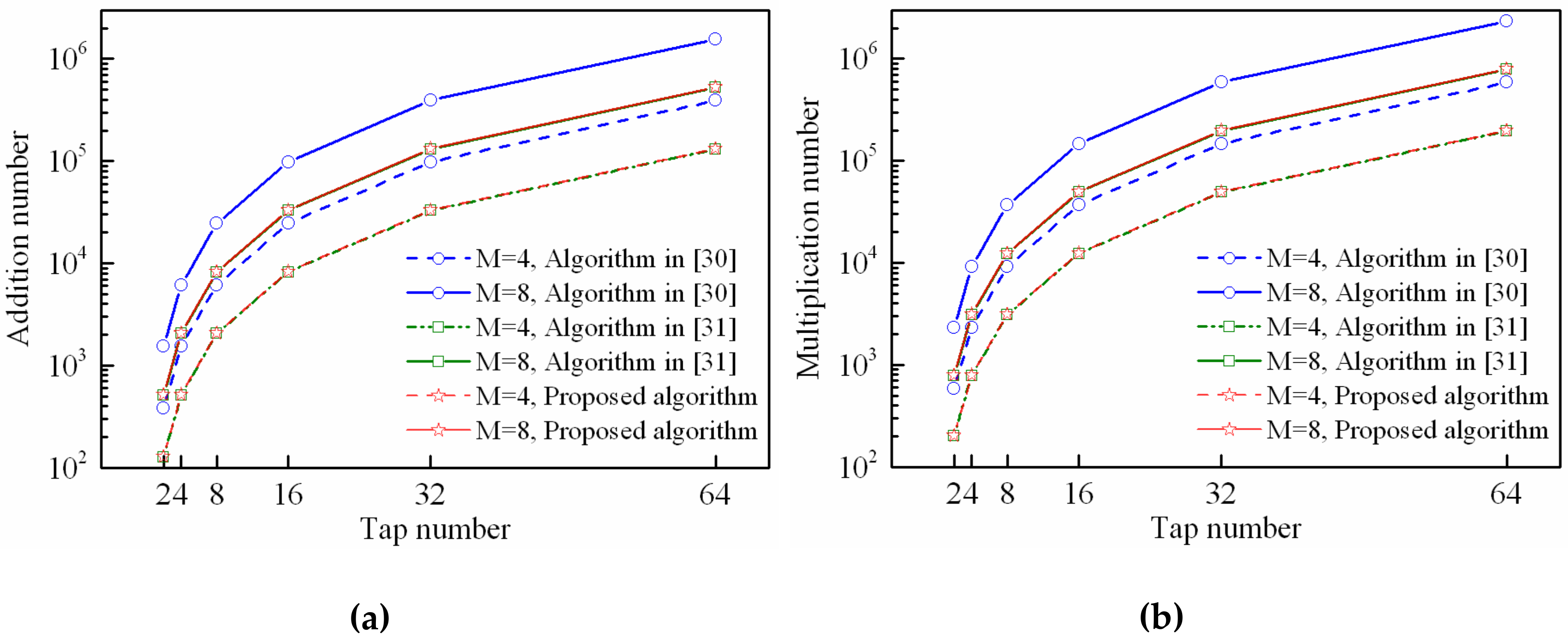
4.4. Computational Complexity Performance
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kaplan, E.D.; Hegarty, C.J. GPS System Segments. In Understanding GPS—Principles and Applications, 2nd ed.; Artech House: Norwood, MA, USA, 2006; pp. 67–112. [Google Scholar]
- Abedi, M.; Rezaei, M.J.; Mosavi, M.R. Accurate interference mitigation in global positioning system receivers based on double-step short-time Fourier transform. Circuits Syst. Signal Process. 2017, 37, 2450–2470. [Google Scholar] [CrossRef]
- Borio, D.; Li, H.Q.; Closas, P. Huber’s non-linearity for GNSS interference mitigation. Sensors 2018, 18, 2217. [Google Scholar] [CrossRef]
- Chien, Y.R.; Chen, P.Y.; Fang, S.H. Novel anti-Jamming algorithm for GNSS receivers using wavelet-packet-transform-based adaptive predictors. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2017, 602–610. [Google Scholar] [CrossRef]
- Rezaei, M.J.; Mosavi, M.R. Hybrid anti-jamming approach for kinematic global positioning system receivers. IET Signal Process. 2018, 12, 888–895. [Google Scholar] [CrossRef]
- Zhao, H.B.; Hu, Y.N.; Sun, H.; Feng, W.Q. A BDS interference suppression technique based on linear phase adaptive IIR notch filters. Sensors 2018, 18, 1515. [Google Scholar] [CrossRef]
- Chien, Y.R. Design of GPS anti-jamming systems using adaptive notch filters. IEEE Syst. J. 2015, 9, 451–460. [Google Scholar] [CrossRef]
- Xi, J.; Wang, C.; Liu, H.; Wang, L. Completely distributed guaranteed-performance consensualization for high-order multiagent systems with switching topologies. IEEE Trans. Syst. Man Cybern. Syst. 2018, 1–11. [Google Scholar] [CrossRef]
- Xi, J.; Wang, C.; Liu, H.; Wang, Z. Dynamic output feedback guaranteed-cost synchronization for multiagent networks with given cost budgets. IEEE Access 2018, 6, 28923–28935. [Google Scholar] [CrossRef]
- Widrow, B.; Mantey, P.E.; Griffiths, L.J.; Goode, B.B. Adaptive antenna systems. Proc. IEEE 1967, 55, 2143–2159. [Google Scholar] [CrossRef]
- Gao, G.X.; Sgammini, M.; Lu, M.Q.; Kubo, N. Protecting GNSS receivers from jamming and interference. Proc. IEEE 2016, 104, 1327–1338. [Google Scholar] [CrossRef]
- Jang, J.; Seo, S.; Ahn, W.; Lee, J.; Park, J. Performance analysis of an interference cancellation technique for radio navigation. IET Radar Sonar Nav. 2018, 12, 426–432. [Google Scholar] [CrossRef]
- Compton, R.T. The power-inversion adaptive array: Concept and performance. IEEE Trans. Aerosp. Electron. Syst. 1979, 15, 803–814. [Google Scholar] [CrossRef]
- Arribas, J.; Fernandez-Prades, C.; Closas, P. Antenna array based GNSS signal acquisition for interference mitigation. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 223–243. [Google Scholar] [CrossRef]
- Broumandan, A.; Jafarnia-Jahromi, A.; Daneshmand, S.; Lachapelle, G. Overview of spatial processing approaches for GNSS structural interference detection and mitigation. Proc. IEEE 2016, 104, 1246–1257. [Google Scholar] [CrossRef]
- Chen, F.Q.; Nie, J.W.; Ni, S.J. Combined algorithm for interference suppression and signal acquisition in GNSS receiver. Electron. Lett. 2017, 53, 274–275. [Google Scholar] [CrossRef]
- Fante, R.L.; Vaccaro, J. Wideband cancellation of interference in a GPS receiver array. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 549–564. [Google Scholar] [CrossRef]
- Daneshmand, S.; Jahromi, A.J.; Broumandan, A. GNSS space–time interference mitigation and attitude determination in the presence of interference signals. Sensors 2015, 15, 12180–12204. [Google Scholar] [CrossRef]
- Dai, X.Z.; Nie, J.W.; Chen, F.Q.; Qu, G. Distortionless space–time adaptive processor based on MVDR beamformer for GNSS receiver. IET Radar Sonar Nav. 2017, 11, 1488–1494. [Google Scholar] [CrossRef]
- Lee, K.; Lee, J. Design and evaluation of symmetric space–time adaptive processing of an array antenna for precise global navigation satellite system receivers. IET Signal Process. 2017, 11, 758–764. [Google Scholar] [CrossRef]
- Fertig, L.B. Analytical expressions for space–time adaptive processing (STAP) performance. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 42–53. [Google Scholar] [CrossRef]
- Compton, R.T. The tripole antenna: An adaptive array with full polarization flexibility. IEEE. Trans. Antennas Propag. 1981, 29, 944–952. [Google Scholar] [CrossRef] [Green Version]
- Compton, R.T. On the performance of a polarization sensitive adaptive array. IEEE Trans. Antennas Propag. 1981, 29, 718–725. [Google Scholar] [CrossRef]
- Cheuk, W.C.; Trinkle, M.; Gray, D.A. Null-steering LMS dual-polarised adaptive antenna arrays for GPS. Positioning 2005, 4, 258–267. [Google Scholar] [CrossRef]
- Wang, J.; Amin, M.G. Multiple interference cancellation performance for GPS receivers with dual-polarized antenna arrays. EURASIP J. Adv. Signal Process. 2008, 2008, 1–13. [Google Scholar] [CrossRef]
- Zhan, Y.H.; Li, S.X.; Wang, Z. Algorithm and performance analysis of GPS signal dual-polarized antenna anti-jamming. J. Nat. Uni. Def. Technol. 2009, 31, 95–98. [Google Scholar]
- Fohlmeister, F.; Iliopoulos, A.; Sgammini, M.; Antreich, F.; Seo, J. Dual polarization beamforming algorithm for multipath mitigation in GNSS. Signal Process. 2017, 138, 86–97. [Google Scholar] [CrossRef]
- Fante, R.L.; Vaccaro, J.J. Evaluation of adaptive space–time-polarization cancellation of broadband interference. In Proceedings of the IEEE Position Location and Navigation Symposium, Palms Springs, CA, USA, 15–18 April 2002. [Google Scholar] [CrossRef]
- Fante, R.L. Principles of adaptive space–time-polarization cancellation of broadband interference. In Proceedings of the 17th International Technical Meeting of the Satellite Division of the Institute of Navigation, Long Beach, CA, USA, 21–24 September 2004. [Google Scholar]
- Park, K.; Lee, D.; Seo, J. Dual-polarized GPS antenna array algorithm to adaptively mitigate a large number of interference signals. Aerosp. Sci. Technol. 2018, 78, 387–396. [Google Scholar] [CrossRef]
- Gupta, I. Adaptive arrays for multiple simultaneous desired signals. IEEE Trans. Aerosp. Electron. Syst. 1983, 761–767. [Google Scholar] [CrossRef]
- Li, M.; Dempster, A.G.; Balaei, A.T.; Rizos, C.; Wang, F. Switchable Beam Steering/Null Steering Algorithm for CW Interference Mitigation in GPS C/A Code Receivers. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1564–1579. [Google Scholar] [CrossRef] [Green Version]
- Amin, M.G.; Wang, X.; Zhang, Y.D.; Ahmad, F.; Aboutanios, E. Sparse Arrays and Sampling for Interference Mitigation and DOA Estimation in GNSS. Proc. IEEE 2016, 104, 1302–1317. [Google Scholar] [CrossRef]
- Sun, W.; Amin, M.G. A self-coherence anti-jamming GPS receiver. IEEE Trans. Signal Process. 2005, 53, 3910–3915. [Google Scholar] [CrossRef]
- Rong, Z.; Rappaport, T.S. Simulation of Multitarget adaptive algorithms for wireless CDMA systems. In Proceedings of the IEEE Vehicular Technology Conference, Phoenix, AZ, USA, 4–7 May 1997. [Google Scholar] [CrossRef]


| Polarization Mode | ||
|---|---|---|
| HP | 0 | 0,π |
| VP | π/2 | 0,π |
| RHCP | π/4 | π/2 |
| LHCP | π/4 | −π/2 |
| EP | [0,π/2] | [−π,π) |
| Scenario | Incident Signal | SNR/INR | Spatial Parameter | Polarized Parameter | |
|---|---|---|---|---|---|
| Amplitude Ratio | Phase Difference | ||||
| 1 | BD2 B3 (PRN 1) | −20 dB | 0 | π/4 | π/2 |
| BD2 B3 (PRN 2) | −20 dB | −π/6 | π/4 | π/2 | |
| Wideband interference (EP) | 40 dB | π/3 | π/6 | π/3 | |
| 2 | BD2 B3 (PRN 1) | −20 dB | π/36 | π/4 | π/2 |
| BD2 B3 (PRN 2) | −20 dB | π/12 | π/4 | π/2 | |
| BD2 B3 (PRN 3) | −20 dB | π/4 | π/4 | π/2 | |
| BD2 B3 (PRN 4) | −20 dB | 5π/12 | π/4 | π/2 | |
| BD2 B3 (PRN 5) | −20 dB | 4π/9 | π/4 | π/2 | |
| BD2 B3 (PRN 6) | −20 dB | 17π/36 | π/4 | π/2 | |
| BD2 B3 (PRN 7) | −20 dB | −π/36 | π/4 | π/2 | |
| BD2 B3 (PRN 8) | −20 dB | −π/12 | π/4 | π/2 | |
| BD2 B3 (PRN 9) | −20 dB | −π/4 | π/4 | π/2 | |
| BD2 B3 (PRN 10) | −20 dB | −5π/12 | π/4 | π/2 | |
| BD2 B3 (PRN 11) | −20 dB | −4π/9 | π/4 | π/2 | |
| BD2 B3 (PRN 12) | −20 dB | −17π/36 | π/4 | π/2 | |
| Wideband interference (HP) | 40 dB | [−5π/36, −7π/36] | 0 | π | |
| Wideband interference (VP) | 40 dB | [11π/36, 13π/36] | π/2 | π | |
| Wideband interference (LHCP) | 40 dB | [5π/36, 7π/36] | π/4 | −π/2 | |
| Wideband interference (RHCP) | 40 dB | [−11π/36, −13π/36] | π/4 | π/2 | |
| 3 | BD2 B3 (PRN 1) | −20 dB | π/36 | π/4 | π/2 |
| BD2 B3 (PRN 2) | −20 dB | π/12 | π/4 | π/2 | |
| BD2 B3 (PRN 3) | −20 dB | π/4 | π/4 | π/2 | |
| BD2 B3 (PRN 4) | −20 dB | 5π/12 | π/4 | π/2 | |
| BD2 B3 (PRN 5) | −20 dB | 4π/9 | π/4 | π/2 | |
| BD2 B3 (PRN 6) | −20 dB | 17π/36 | π/4 | π/2 | |
| BD2 B3 (PRN 7) | −20 dB | −π/36 | π/4 | π/2 | |
| BD2 B3 (PRN 8) | −20 dB | −π/12 | π/4 | π/2 | |
| BD2 B3 (PRN 9) | −20 dB | −π/4 | π/4 | π/2 | |
| BD2 B3 (PRN 10) | −20 dB | −5π/12 | π/4 | π/2 | |
| BD2 B3 (PRN 11) | −20 dB | −4π/9 | π/4 | π/2 | |
| BD2 B3 (PRN 12) | −20 dB | −17π/36 | π/4 | π/2 | |
| Wideband interference (RHCP) | 40 dB | [−5π/36, −7π/36] | π/4 | π/2 | |
| Wideband interference (RHCP) | 40 dB | [11π/36, 13π/36] | π/4 | π/2 | |
| Wideband interference (RHCP) | 40 dB | [5π/36, 7π/36] | π/4 | π/2 | |
| Wideband interference (RHCP) | 40 dB | [−11π/36, −13π/36] | π/4 | π/2 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Yao, Z.; Yang, J.; Fan, Z. A Novel Beamforming Algorithm for GNSS Receivers with Dual-Polarized Sensitive Arrays in the Joint Space–Time-Polarization Domain. Sensors 2018, 18, 4506. https://doi.org/10.3390/s18124506
Wang H, Yao Z, Yang J, Fan Z. A Novel Beamforming Algorithm for GNSS Receivers with Dual-Polarized Sensitive Arrays in the Joint Space–Time-Polarization Domain. Sensors. 2018; 18(12):4506. https://doi.org/10.3390/s18124506
Chicago/Turabian StyleWang, Haiyang, Zhicheng Yao, Jian Yang, and Zhiliang Fan. 2018. "A Novel Beamforming Algorithm for GNSS Receivers with Dual-Polarized Sensitive Arrays in the Joint Space–Time-Polarization Domain" Sensors 18, no. 12: 4506. https://doi.org/10.3390/s18124506
APA StyleWang, H., Yao, Z., Yang, J., & Fan, Z. (2018). A Novel Beamforming Algorithm for GNSS Receivers with Dual-Polarized Sensitive Arrays in the Joint Space–Time-Polarization Domain. Sensors, 18(12), 4506. https://doi.org/10.3390/s18124506




