Error Analysis of the K-Rb-21Ne Comagnetometer Space-Stable Inertial Navigation System
Abstract
:1. Introduction
2. Characteristic and Error Model of the Comagnetometer
2.1. Characteristic
2.2. Error Model
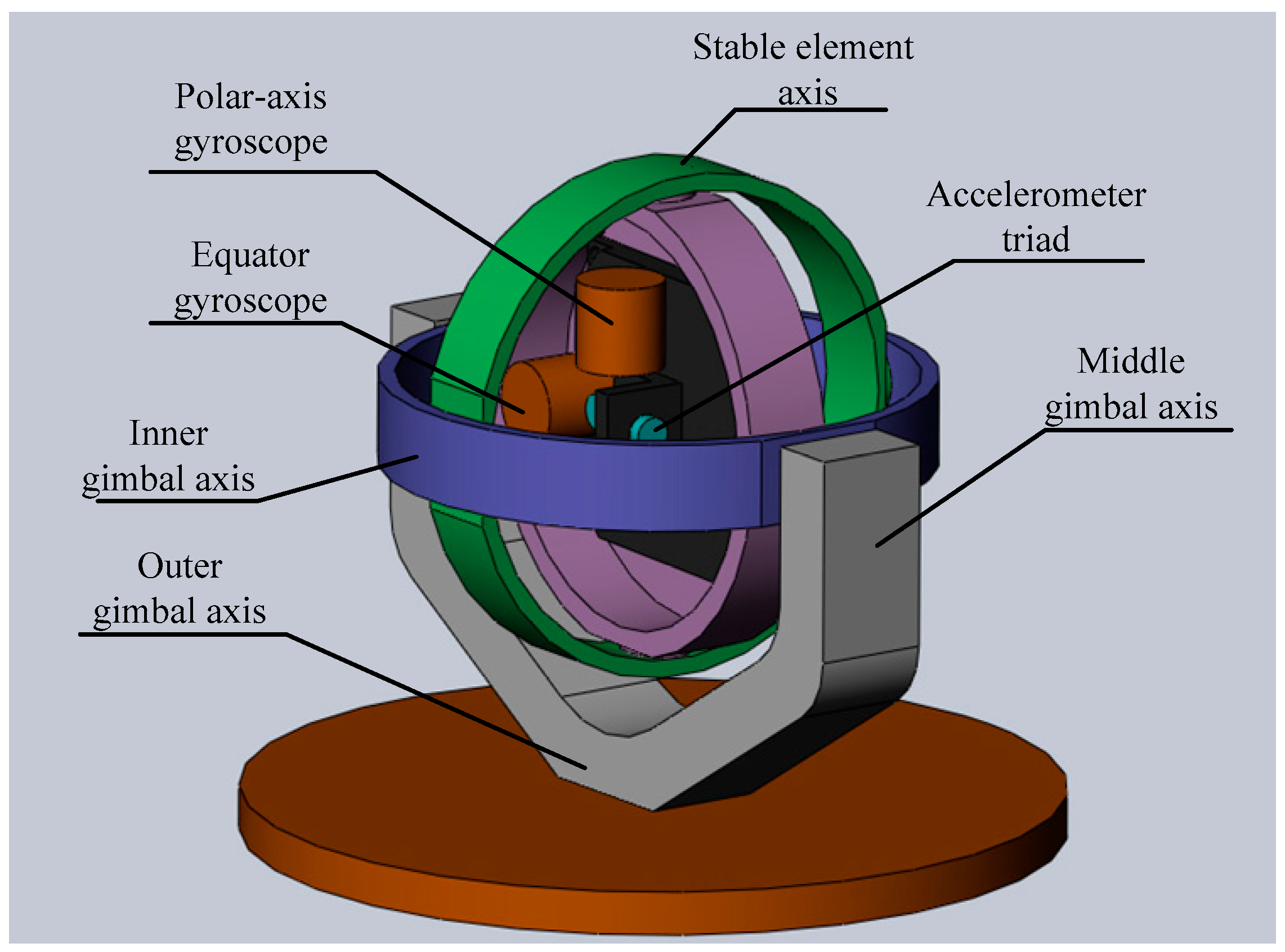
3. Comagnetometer Space-Stable Platform
3.1. Structure of the Space-Stable Platform
3.2. Discussion of the Requirements for the Comagnetometer Prototype
4. Error Analysis of the Comagnetometer Space-Stable INS
4.1. Mechanization Equation
4.2. Error Model of the System
4.3. Error Propagation Rule
5. Simulation Tests
5.1. Numerical Simulation of the Mathematical Model
5.2. Numerical Simulation Based on Semi-Physical Data
6. Conclusions and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fang, J.; Qin, J. Advances in atomic gyroscopes: A view from inertial navigation applications. Sensors 2012, 12, 6331–6346. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.G.; Williams, T.C. Strategic inertial navigation systems-High-accuracy inertially stabilized platforms for hostile environments. IEEE Control Syst. 2008, 28, 65–85. [Google Scholar] [CrossRef]
- Dong, H.; Fang, J.; Qin, J.; Chen, Y. Analysis of the electrons-nuclei coupled atomic gyroscope. Optics Communications. Opt. Commun. 2011, 284, 2886–2889. [Google Scholar] [CrossRef]
- Durfee, D.S.; Shaham, Y.K.; Kasevich, M.A. Long-term stability of an area-reversible atom-interferometer sagnac gyroscope. Phys. Rev. Lett. 2005, 97, 387–392. [Google Scholar] [CrossRef] [PubMed]
- Dubetsky, B.; Kasevich, M.A. Atom interferometer as a selective sensor of rotation or gravity. Phys. Rev. A 2006, 74, 154. [Google Scholar] [CrossRef]
- Gustavson, T.L.; Landragin, A.; Kasevich, M.A. Rotation sensing with a dual atom-interferometer Sagnac gyroscope. Class. Quantum Gravity 2000, 17, 2385–2398. [Google Scholar] [CrossRef]
- Dutta, I.; Savoie, D.; Fang, B.; Venon, B.; Alzar, C.; Geiger, R.; Landragin, A. Continuous cold-atom inertial sensor with 1 nrad/sec rotation stability. Phys. Rev. Lett. 2016, 116, 183003. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; Rong, X.; Zhao, N.; Wang, Y.; Yang, J.; Liu, B. Preserving electron spin coherence in solids by optimal dynamical decoupling. Nature 2010, 461, 1265–1268. [Google Scholar] [CrossRef] [PubMed]
- Shi, F.; Zhang, Q.; Wang, P.; Sun, H.; Wang, J.; Rong, X.; Chen, M.; Ju, C.; Reinhard, F.; Chen, H.; et al. Protein imaging. Single-protein spin resonance spectroscopy under ambient conditions. Science 2015, 347, 1135–1138. [Google Scholar] [CrossRef] [PubMed]
- Kornack, T.W.; Ghosh, R.K.; Romalis, M.V. Nuclear spin gyroscope based on an atomic comagnetometer. Phys. Rev. Lett. 2005, 95, 230801. [Google Scholar] [CrossRef] [PubMed]
- Allred, J.C.; Lyman, R.N.; Kornack, T.W.; Romalis, M.V. High-sensitivity atomic magnetometer unaffected by spin-exchange relaxation. Phys. Rev. Lett. 2002, 89, 130801. [Google Scholar] [CrossRef] [PubMed]
- Kitching, J.; Donley, E.A.; Hodby, E.; Shkel, A.; Eklund, E.J. Compact Atomic Magnetometer and Gyroscope Based on a Diverging Laser Beam. U.S. Patent 7872473, 18 January 2011. [Google Scholar]
- Fang, J.; Chen, Y.; Zou, S.; Liu, X.; Hu, Z.; Quan, W.; Yuan, H.; Ding, M. Low frequency magnetic field suppression in an atomic spin co-magnetometer with a large electron magnetic field. J. Phys. B Atomic Mol. Opt. Phys. 2016, 49, 065006. [Google Scholar] [CrossRef]
- Li, R.; Fan, W.; Jiang, L.; Duan, L.; Quan, W.; Fang, J. Rotation sensing using a K-Rb-21Ne comagnetometer. Phys. Rev. A 2016, 94, 032109. [Google Scholar] [CrossRef]
- Dong, H.; Gao, Y. Comparison of Compensation Mechanism Between an NMR Gyroscope and an SERF Gyroscope. IEEE Sens. J. 2017, 17, 4052–4055. [Google Scholar] [CrossRef]
- Qin, J.; Fang, J.; Wan, S. Experimental design of a dual axis Atomic Spin Gyroscope. In Proceedings of the 2012 8th IEEE International Symposium on Instrumentation and Control Technology (ISICT), London, UK, 11–13 July 2012; pp. 24–27. [Google Scholar]
- Ochoa, J.E.; Ochoa, J.E.; Correa, M.M.; Valencia, A.M.; Mcewen, J.G.; Gallo, J.A.; Bilo, G. Stable three-axis nuclear spin gyroscope in diamond. Phys. Rev. A 2012, 86, 12184–12188. [Google Scholar]
- Fang, J.; Qin, J.; Wan, S.; Chen, Y.; Li, R. Atomic spin gyroscope based on 129Xe-Cs comagnetometer. Chin. Sci. Bull. 2013, 58, 1512–1515. [Google Scholar] [CrossRef]
- Zhang, H.; Zou, S.; Chen, X. Optimal modeling on magnetic shielding cylinder of atomic spin gyroscope considering transverse shielding factor. In Proceedings of the 2015 IEEE Metrology for Aerospace (MetroAeroSpace), Benevento, Italy, 4–5 June 2015; pp. 6–8. [Google Scholar]
- Fang, J.; Wan, S.; Yuan, H. Dynamics of an all-optical atomic spin gyroscope. Appl. Opt. 2013, 52, 7220–7227. [Google Scholar] [CrossRef] [PubMed]
- Quan, W.; Lv, L.; Liu, B. Modeling and optimizing of the random atomic spin gyroscope drift based on the atomic spin gyroscope. Rev. Sci. Instrum. 2014, 85, 113104. [Google Scholar] [CrossRef] [PubMed]
- Duan, L.; Quan, W.; Jiang, L.; Fan, W.; Ding, M.; Hu, Z.; Fang, J. Common-mode noise reduction in an atomic spin gyroscope using optical differential detection. Appl. Opt. 2017, 56, 7734–7740. [Google Scholar] [CrossRef] [PubMed]
- Zou, S.; Zhang, H.; Chen, X. Modeling and filter algorithm analysis of all-optical atomic spin gyroscope’s random drift. In Proceedings of the 2015 IEEE Metrology for Aerospace (MetroAeroSpace), Benevento, Italy, 4–5 June 2015; pp. 207–219. [Google Scholar]
- Zou, S.; Zhang, H.; Chen, X.; Chen, Y.; Fang, J. A novel calibration method research of the scale factor for the all-optical atomic spin inertial measurement device. J. Opt. Soc. Korea 2015, 19, 415–420. [Google Scholar] [CrossRef]
- Jiang, L.; Quan, W.; Li, R.; Duan, L.; Fan, W.; Wang, Z.; Liu, F.; Xing, L.; Fang, J. Suppression of the cross-talk effect in a dual-axis K-Rb-21Ne comagnetometer. Phys. Rev. A 2017, 95, 062103. [Google Scholar] [CrossRef]
- Quan, W.; Li, Y.; Liu, B. Simultaneous measurement of magnetic field and inertia based on hybrid optical pumping. EPL 2015, 110, 60002. [Google Scholar] [CrossRef]
- Fang, J.; Wang, T.; Zhang, H.; Li, Y.; Cai, H.-W. In-situ measurement of magnetic field gradient in a magnetic shield by a spin-exchange relaxation-free magnetometer. Chin. Phys. B 2015, 24, 060702. [Google Scholar] [CrossRef]
- Karaulanov, T.; Savukov, I.; Kim, Y.J. Spin-exchange relaxation-free magnetometer with nearly parallel pump and probe beams. Meas. Sci. Technol. 2016, 27, 055002. [Google Scholar] [CrossRef]
- Elton, O.L.; Moore, J.P. Marine ESG Navigation as a Capability for the Present. Navigation 1973, 20, 126–136. [Google Scholar] [CrossRef]
- Dushman, A.; Sandberg, H. Accuracy of ESG monitor/sins inertial navigation system. In Proceedings of the Ocean 73 IEEE International Conference on Engineering in the Ocean Environment, Seattle, WA, USA, 25–28 September 1973; pp. 602–610. [Google Scholar]
- Gao, Z. Error Propagation Property of Inertial Navigation System. In Inertial Navigation System Technology, 1st ed.; Tsinghua University Press: Beijing, China, 2012; pp. 279–289. [Google Scholar]
- Wu, Q.; Han, F. New optimal approach to space-stable inertial navigation system. In Proceedings of the 2011 10th International Conference on Electronic Measurement & Instruments (ICEMI), Chengdu, China, 16–19 August 2011; pp. 296–299. [Google Scholar]
- Nash, R.A.; Levine, S.A.; Roy, K.J. Error analysis of space-stable inertial navigation systems. IEEE Trans. Aerosp. Electron. Syst. 1971, 7, 617–629. [Google Scholar] [CrossRef]
- Hutchinson, C.E.; Nash, R.A. Comparison of Error Propagation in Local-Level and Space-Stable Inertial Systems. IEEE Trans. Aerosp. Electron. Syst. 1971, 7, 1138–1142. [Google Scholar] [CrossRef]
- Nash, R.A.; Hutchinson, C.E. Altitude damping of space-stable inertial navigation systems. IEEE Trans. Aerosp. Electron. Syst. 1973, 9, 18–27. [Google Scholar] [CrossRef]
- Hutchinson, C.E.; Fagan, J.H. Kalman filter design considerations for space-stable inertial navigation systems. IEEE Trans. Aerosp. Electron. Syst. 1973, 9, 306–319. [Google Scholar] [CrossRef]



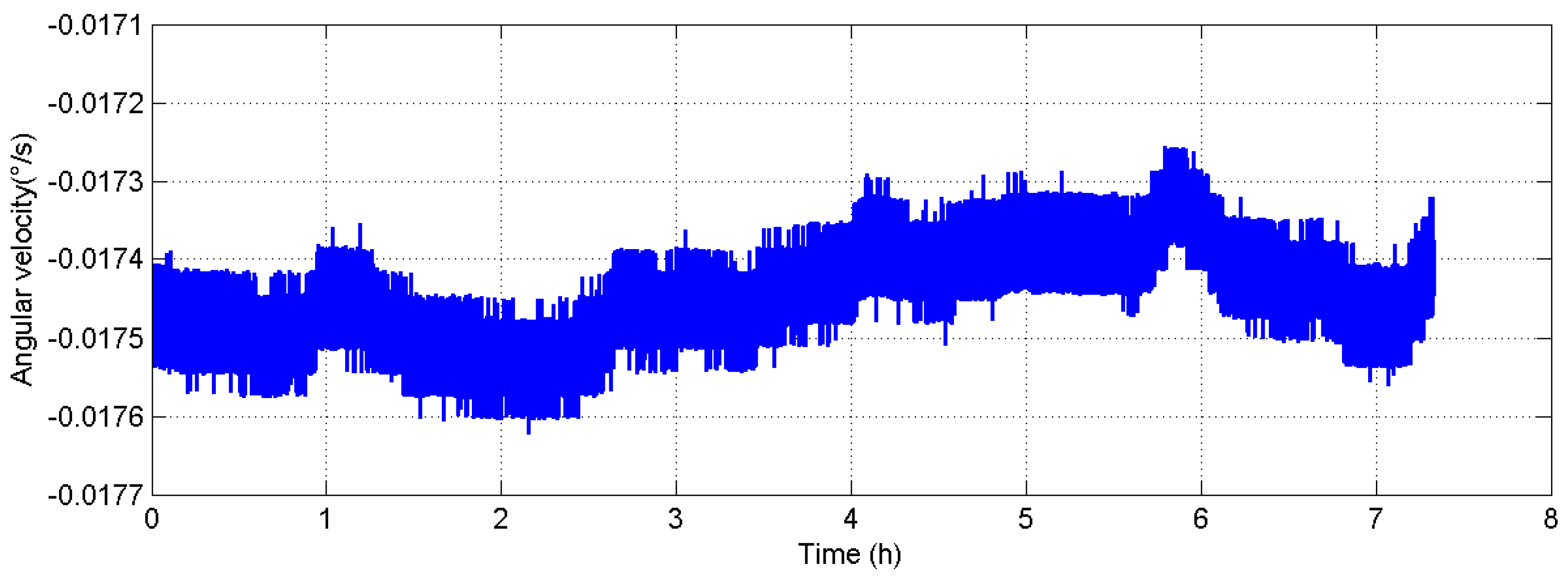

| Error Term | Latitude Error | Longitude Error |
|---|---|---|
| - | ||
| - |
| Error Term | Max Latitude Error | Max Longitude Error |
|---|---|---|
| 0.98 nmile | 0.65 nmile | |
| 1.01 nmile | 0.65 nmile | |
| 0.02 nmile | 0.8 nmile | |
| 1.41 nmile | 0.95 nmile | |
| 1.45 nmile | 0.92 nmile | |
| 0.02 nmile | 1.18 nmile |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Q.; Yang, G.; Quan, W.; Song, N.; Tu, Y.; Liu, Y. Error Analysis of the K-Rb-21Ne Comagnetometer Space-Stable Inertial Navigation System. Sensors 2018, 18, 670. https://doi.org/10.3390/s18020670
Cai Q, Yang G, Quan W, Song N, Tu Y, Liu Y. Error Analysis of the K-Rb-21Ne Comagnetometer Space-Stable Inertial Navigation System. Sensors. 2018; 18(2):670. https://doi.org/10.3390/s18020670
Chicago/Turabian StyleCai, Qingzhong, Gongliu Yang, Wei Quan, Ningfang Song, Yongqiang Tu, and Yiliang Liu. 2018. "Error Analysis of the K-Rb-21Ne Comagnetometer Space-Stable Inertial Navigation System" Sensors 18, no. 2: 670. https://doi.org/10.3390/s18020670
APA StyleCai, Q., Yang, G., Quan, W., Song, N., Tu, Y., & Liu, Y. (2018). Error Analysis of the K-Rb-21Ne Comagnetometer Space-Stable Inertial Navigation System. Sensors, 18(2), 670. https://doi.org/10.3390/s18020670





