Electrode Coverage Optimization for Piezoelectric Energy Harvesting from Tip Excitation
Abstract
:1. Introduction
2. Theoretical Modelling of Piezoelectric Harvester with Varying Electrode Coverage
2.1. Harvester Design and Configuration
2.2. Modelling of Harvester with Variable Electrode
2.3. Analysis of Electromechanical Dynamics
3. Experimental Set-Up
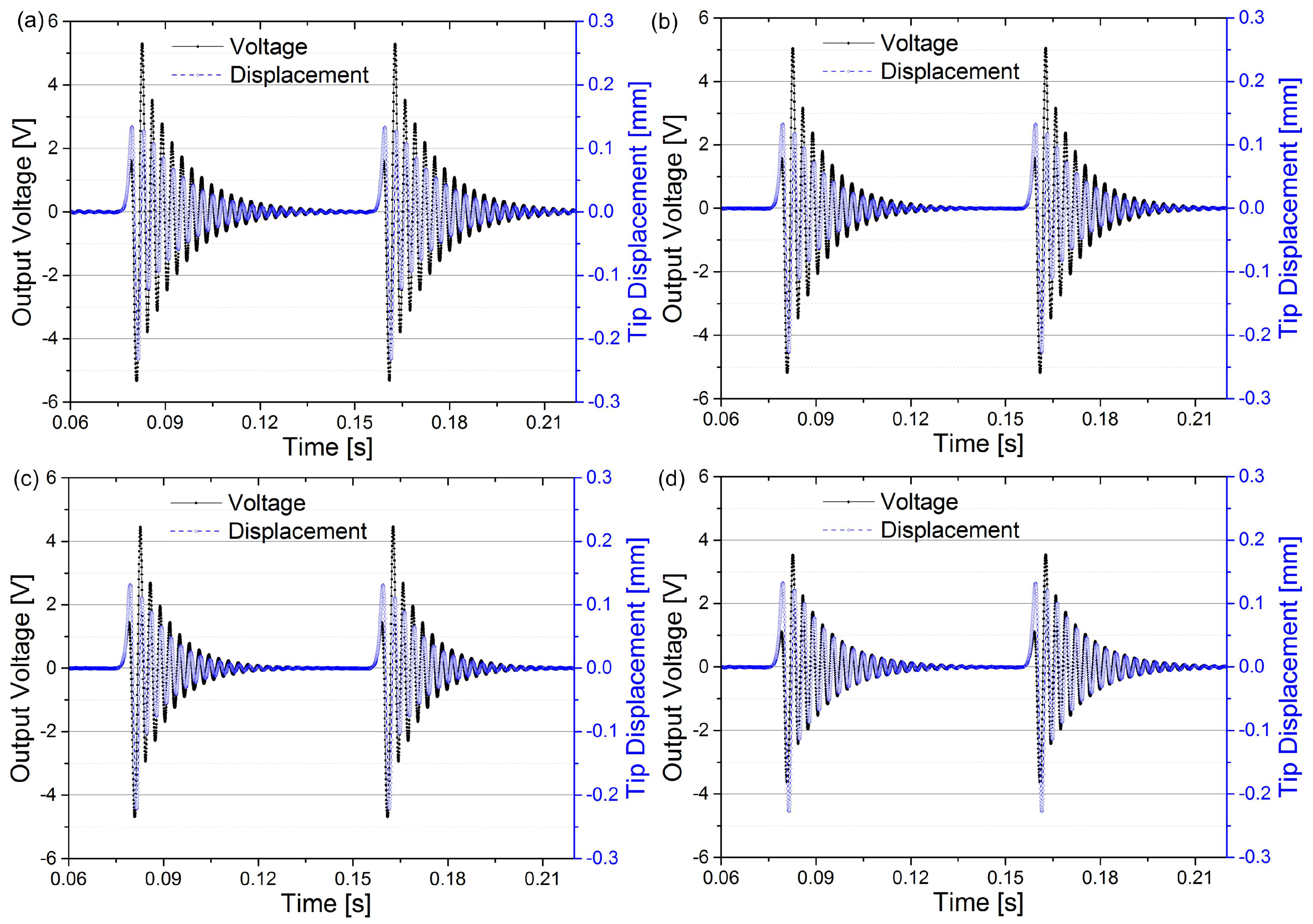
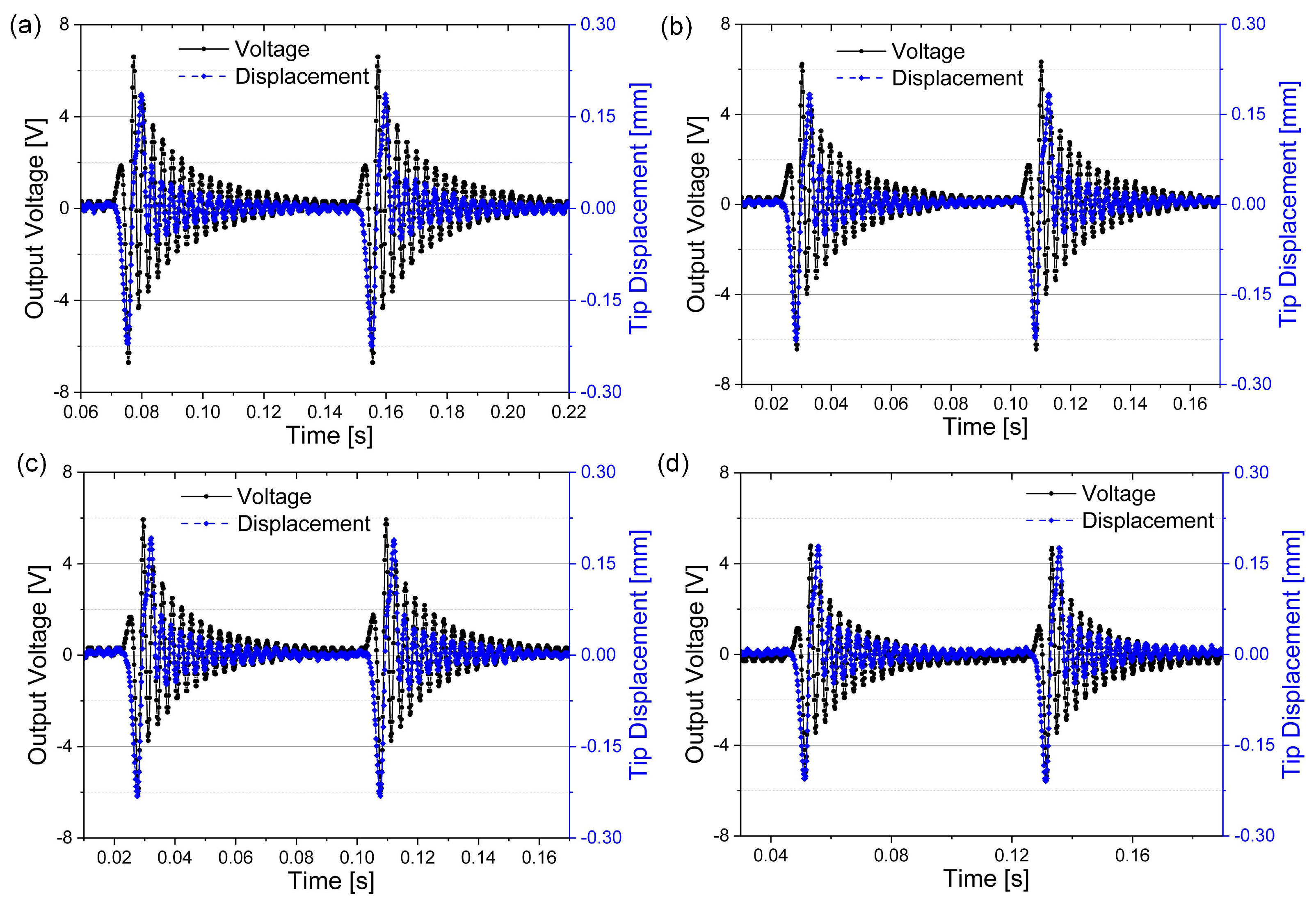
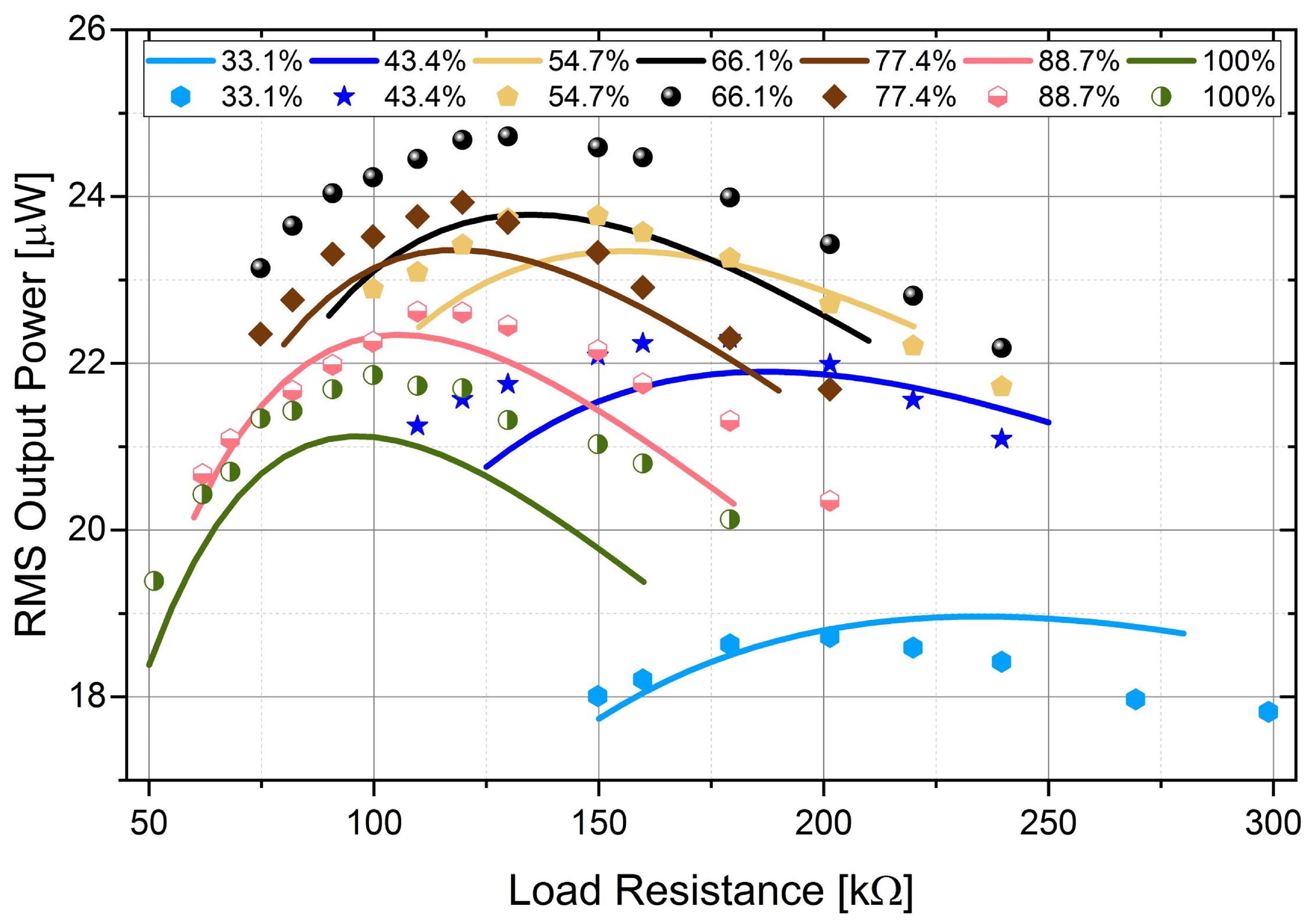
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mitcheson, P.D.; Yeatman, E.M.; Rao, G.K.; Holmes, A.S.; Green, T.C. Energy Harvesting From Human and Machine Motion for Wireless Electronic Devices. Proc. IEEE 2008, 96, 1457–1486. [Google Scholar] [CrossRef] [Green Version]
- Nabavi, S.; Zhang, L. Portable Wind Energy Harvesters for Low-Power Applications: A Survey. Sensors 2016, 16, 1101. [Google Scholar] [CrossRef] [PubMed]
- Roundy, S.; Wright, P.K. A piezoelectric vibration based generator for wireless electronics. Smart Mater. Struct. 2004, 13, 1131–1142. [Google Scholar] [CrossRef]
- Fan, K.; Chang, J.; Chao, F.; Pedrycz, W. Design and development of a multipurpose piezoelectric energy harvester. Energy Convers. Manag. 2015, 96, 430–439. [Google Scholar] [CrossRef]
- Richards, C.D.; Anderson, M.J.; Bahr, D.F.; Richards, R.F. Efficiency of energy conversion for devices containing a piezoelectric component. J. Micromech. Microeng. 2004, 14, 717–721. [Google Scholar] [CrossRef]
- Bowen, C.R.; Kim, H.A.; Weaver, P.M.; Dunn, S. Piezoelectric and ferroelectric materials and structures for energy harvesting applications. Energy Environ. Sci. 2014, 7, 25–44. [Google Scholar] [CrossRef] [Green Version]
- Goldschmidtboeing, F.; Woias, P. Characterization of different beam shapes for piezoelectric energy harvesting. J. Micromech. Microeng. 2008, 18, 104013. [Google Scholar] [CrossRef]
- Park, J.; Lee, S.; Kwak, B.M. Design optimization of piezoelectric energy harvester subject to tip excitation. J. Mech. Sci. Technol. 2012, 26, 137–143. [Google Scholar] [CrossRef]
- Dhakar, L.; Liu, H.; Tay, F.; Lee, C. A new energy harvester design for high power output at low frequencies. Sens. Actuators A Phys. 2013, 199, 344–352. [Google Scholar] [CrossRef]
- Friswell, M.I.; Adhikari, S. Sensor shape design for piezoelectric cantilever beams to harvest vibration energy. J. Appl. Phys. 2010, 108, 014901. [Google Scholar] [CrossRef]
- Patel, R.; McWilliam, S.; Popov, A.A. A geometric parameter study of piezoelectric coverage on a rectangular cantilever energy harvester. Smart Mater. Struct. 2011, 20, 085004. [Google Scholar] [CrossRef]
- Zhou, S.; Hobeck, J.D.; Cao, J.; Inman, D.J. Analytical and experimental investigation of flexible longitudinal zigzag structures for enhanced multi-directional energy harvesting. Smart Mater. Struct. 2017, 26, 035008. [Google Scholar] [CrossRef]
- Liu, W.; Liu, C.; Ren, B.; Zhu, Q.; Hu, G.; Yang, W. Bandwidth increasing mechanism by introducing a curve fixture to the cantilever generator. Appl. Phys. Lett. 2016, 109, 043905. [Google Scholar] [CrossRef]
- Lee, H.J.; Sherrit, S.; Tosi, L.P.; Walkemeyer, P.; Colonius, T. Piezoelectric Energy Harvesting in Internal Fluid Flow. Sensors 2015, 15, 26039–26062. [Google Scholar] [CrossRef] [PubMed]
- Erturk, A.; Tarazaga, P.A.; Farmer, J.R.; Inman, D.J. Effect of Strain Nodes and Electrode Configuration on Piezoelectric Energy Harvesting From Cantilevered Beams. J. Vib. Acoust. 2009, 131, 011010. [Google Scholar] [CrossRef]
- De Marqui, C.; Erturk, A.; Inman, D.J. Piezoaeroelastic Modeling and Analysis of a Generator Wing with Continuous and Segmented Electrodes. J. Intell. Mater. Syst. Struct. 2010, 21, 983–993. [Google Scholar] [CrossRef]
- Piñeirua, M.; Doaré, O.; Michelin, S. Influence and optimization of the electrodes position in a piezoelectric energy harvesting flag. J. Sound Vib. 2015, 346, 200–215. [Google Scholar] [CrossRef] [Green Version]
- Krishnasamy, M.; Lenka, T. Distributed parameter model for assorted piezoelectric harvester to prevent charge cancellation. IEEE Sens. Lett. 2017, 1, 1–4. [Google Scholar] [CrossRef]
- Gu, L.; Livermore, C. Impact-driven, frequency up-converting coupled vibration energy harvesting device for low frequency operation. Smart Mater. Struct. 2011, 20, 045004. [Google Scholar] [CrossRef]
- Fu, H.; Yeatman, E.M. A methodology for low-speed broadband rotational energy harvesting using piezoelectric transduction and frequency up-conversion. Energy 2017, 125, 152–161. [Google Scholar] [CrossRef]
- Stewart, M.; Weaver, P.M.; Cain, M. Charge redistribution in piezoelectric energy harvesters. Appl. Phys. Lett. 2012, 100, 073901. [Google Scholar] [CrossRef]
- Cho, J.; Anderson, M.; Richards, R.; Bahr, D.; Richards, C. Optimization of electromechanical coupling for a thin-film PZT membrane: I. Modeling. J. Micromech. Microeng. 2005, 15, 1797–1803. [Google Scholar] [CrossRef]
- Du, S.; Jia, Y.; Chen, S.T.; Zhao, C.; Sun, B.; Arroyo, E.; Seshia, A.A. A new electrode design method in piezoelectric vibration energy harvesters to maximize output power. Sens. Actuators A Phys. 2017, 263, 693–701. [Google Scholar] [CrossRef]
- Tai, W.C.; Zuo, L. On optimization of energy harvesting from base-excited vibration. J. Sound Vib. 2017, 411, 47–59. [Google Scholar] [CrossRef]
- Wickenheiser, A.M.; Garcia, E. Broadband vibration-based energy harvesting improvement through frequency up-conversion by magnetic excitation. Smart Mater. Struct. 2010, 19, 065020. [Google Scholar] [CrossRef]
- Kathpalia, B.; Tan, D.; Stern, I.; Erturk, A. An experimentally validated model for geometrically nonlinear plucking-based frequency up-conversion in energy harvesting. Smart Mater. Struct. 2017, 27, 015024. [Google Scholar] [CrossRef]
- Fu, H.; Yeatman, E.M. A miniaturized piezoelectric turbine with self-regulation for increased air speed range. Appl. Phys. Lett. 2015, 107, 243905. [Google Scholar] [CrossRef]
- Hung, C.F.; Yeh, P.C.; Chung, T.K. A miniature magnetic-force-based three-axis AC magnetic sensor with piezoelectric/vibrational energy-harvesting functions. Sensors 2017, 17, 308. [Google Scholar] [CrossRef] [PubMed]
- Chen, N.; Jung, H.J.; Jabbar, H.; Sung, T.H.; Wei, T. A piezoelectric impact-induced vibration cantilever energy harvester from speed bump with a low-power power management circuit. Sens. Actuators A Phys. 2017, 254, 134–144. [Google Scholar] [CrossRef]
- Chen, N.; Wei, T.; Dong, H.; Jung, H.J.; Lee, S. Alternating Resistive Impedance Matching for an Impact-Type Micro Wind Piezoelectric Energy Harvester. IEEE Trans. Ind. Electron. 2018. [Google Scholar] [CrossRef]
- Xue, T.; Roundy, S. On magnetic plucking configurations for frequency up-converting mechanical energy harvesters. Sens. Actuators A Phys. 2017, 253, 101–111. [Google Scholar] [CrossRef]
- Rezaei-Hosseinabadi, N.; Tabesh, A.; Dehghani, R. A topology and design optimization method for wideband piezoelectric wind energy harvesters. IEEE Trans. Ind. Electron. 2016, 63, 2165–2173. [Google Scholar] [CrossRef]
- Zou, H.X.; Zhang, W.M.; Li, W.B.; Gao, Q.H.; Wei, K.X.; Peng, Z.K.; Meng, G. Design, modeling and experimental investigation of a magnetically coupled flextensional rotation energy harvester. Smart Mater. Struct. 2017, 26, 115023. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Jacquelin, E.; Adhikari, S.; Friswell, M.I. A piezoelectric device for impact energy harvesting. Smart Mater. Struct. 2011, 20, 105008. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations. Smart Mater. Struct. 2009, 18, 025009. [Google Scholar] [CrossRef]
- Akoun, G.; Yonnet, J.P. 3D analytical calculation of the forces exerted between two cuboidal magnets. IEEE Trans. Magn. 1984, 20, 1962–1964. [Google Scholar] [CrossRef]
- Lesieutre, G.; Ottman, G.; Hofmann, H. Damping as a result of piezoelectric energy harvesting. J. Sound Vib. 2004, 269, 991–1001. [Google Scholar] [CrossRef]
- Dicken, J.; Mitcheson, P.D.; Stoianov, I.; Yeatman, E.M. Power-Extraction Circuits for Piezoelectric Energy Harvesters in Miniature and Low-Power Applications. IEEE Trans. Power Electron. 2012, 27, 4514–4529. [Google Scholar] [CrossRef]
- Chen, Z.; Law, M.K.; Mak, P.I.; Ki, W.H.; Martins, R.P. Fully Integrated Inductor-Less Flipping-Capacitor Rectifier for Piezoelectric Energy Harvesting. IEEE J. Solid-State Circuits 2017, 52, 3168–3180. [Google Scholar] [CrossRef]
- Wu, L.; Do, X.D.; Lee, S.G.; Ha, D.S. A self-powered and optimal SSHI circuit integrated with an active rectifier for piezoelectric energy harvesting. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 537–549. [Google Scholar] [CrossRef]







| Symbol | Description | Value |
|---|---|---|
| Beam length and width | ||
| Thickness of piezo layer | 0.1 mm | |
| Thickness of substrate | 0.1 mm | |
| Magnet rotation radius | 12 mm | |
| a × b × c | Driving magnet size | |
| A × B × C | Tip magnet size | |
| Initial gap in z-axis | 3.2 mm | |
| J | Magnetization of magnets | 1.17 T |
| Density of magnets | ||
| Piezoelectric constant | ||
| Piezoelectric charge constant | m/V | |
| Density of piezoelectric material | kg/m | |
| Density of substrate material | kg/m | |
| Y | Young’s modulus of substrate | GPa |
| Relative permittivity constant | 4500 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, H.; Chen, G.; Bai, N. Electrode Coverage Optimization for Piezoelectric Energy Harvesting from Tip Excitation. Sensors 2018, 18, 804. https://doi.org/10.3390/s18030804
Fu H, Chen G, Bai N. Electrode Coverage Optimization for Piezoelectric Energy Harvesting from Tip Excitation. Sensors. 2018; 18(3):804. https://doi.org/10.3390/s18030804
Chicago/Turabian StyleFu, Hailing, Guangzhu Chen, and Nan Bai. 2018. "Electrode Coverage Optimization for Piezoelectric Energy Harvesting from Tip Excitation" Sensors 18, no. 3: 804. https://doi.org/10.3390/s18030804
APA StyleFu, H., Chen, G., & Bai, N. (2018). Electrode Coverage Optimization for Piezoelectric Energy Harvesting from Tip Excitation. Sensors, 18(3), 804. https://doi.org/10.3390/s18030804





