A Review of Multimode Interference in Tapered Optical Fibers and Related Applications
Abstract
:1. Introduction
2. TOF Structures and Their Fabrication
2.1. A Singlemode-Multimode-Singlemode (SMS) Structure
2.2. A Singlemode-Tapered-Multimode-Singlemode (STMS) Structure and Its Fabrication
2.3. Adaptation of an STMS Structure as a Probe Type Structure
2.4. Periodically Tapered SMS Fiber Structures
2.5. Tapered Fiber Structures Incorporating Photonic Crystal Fiber
2.6. Micro Fiber Coupler (MFC) Structure
3. Applications of TOFs as Optical Fiber Sensors
3.1. RI Sensor
3.2. Temperature Sensor
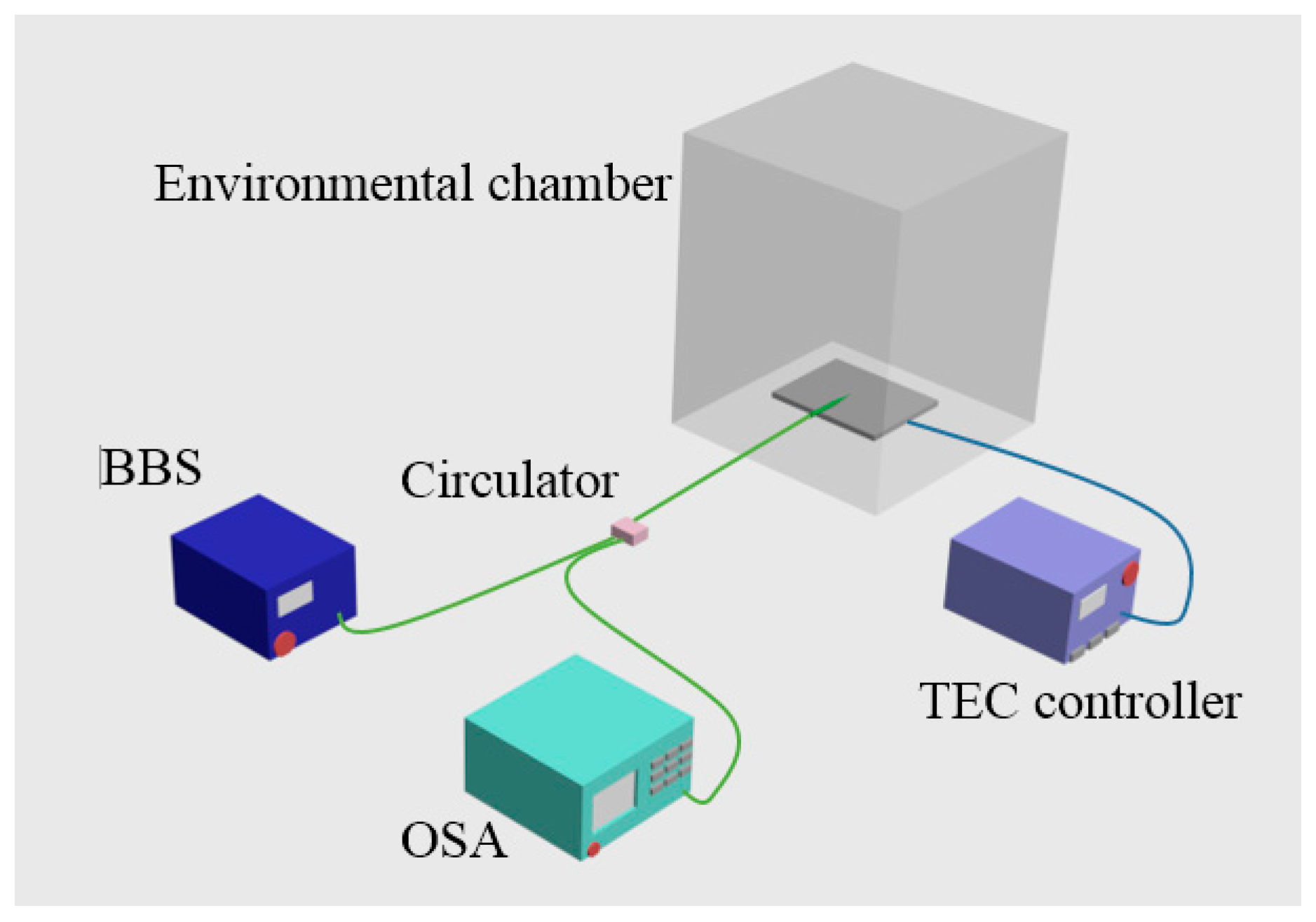
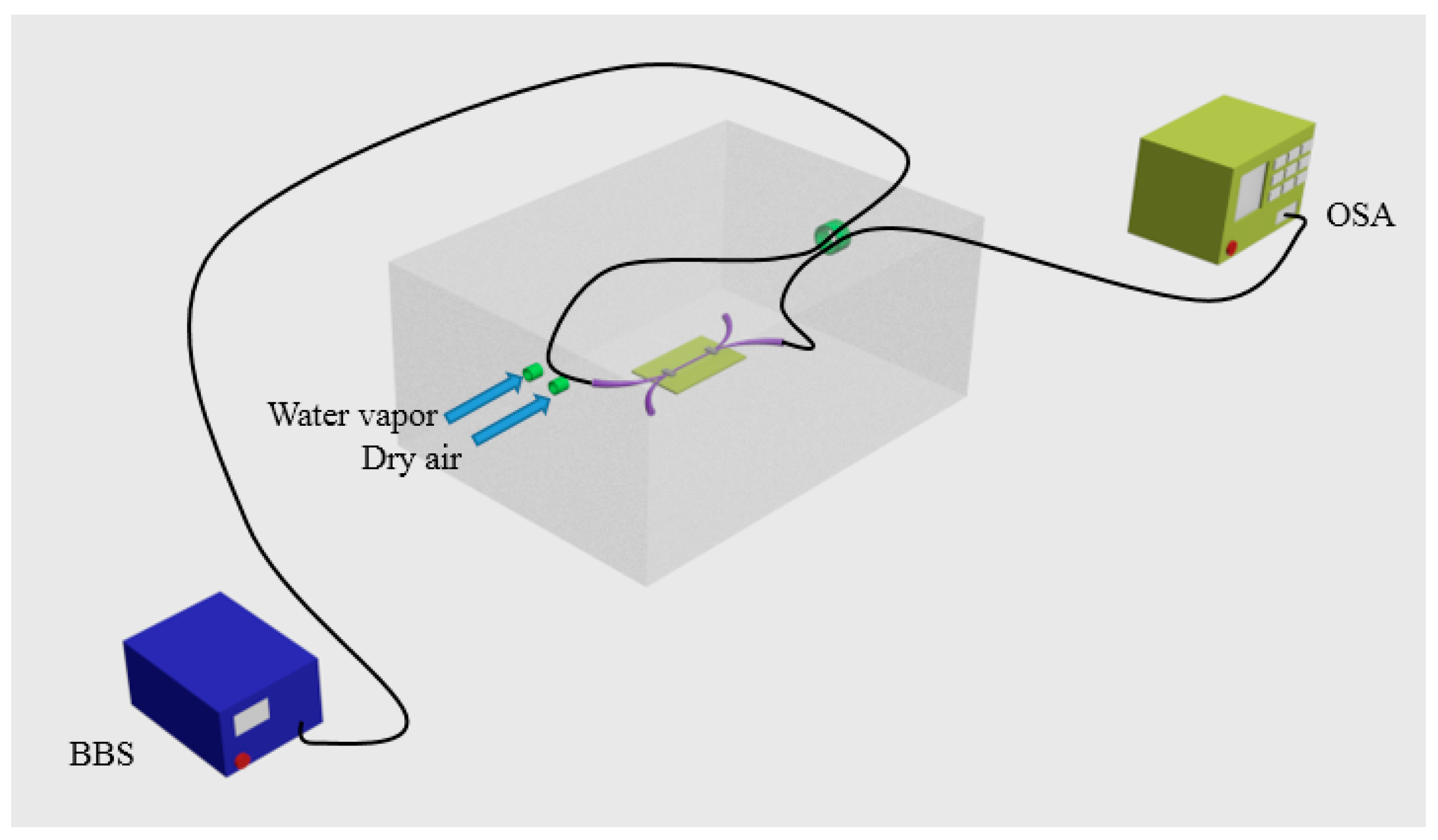
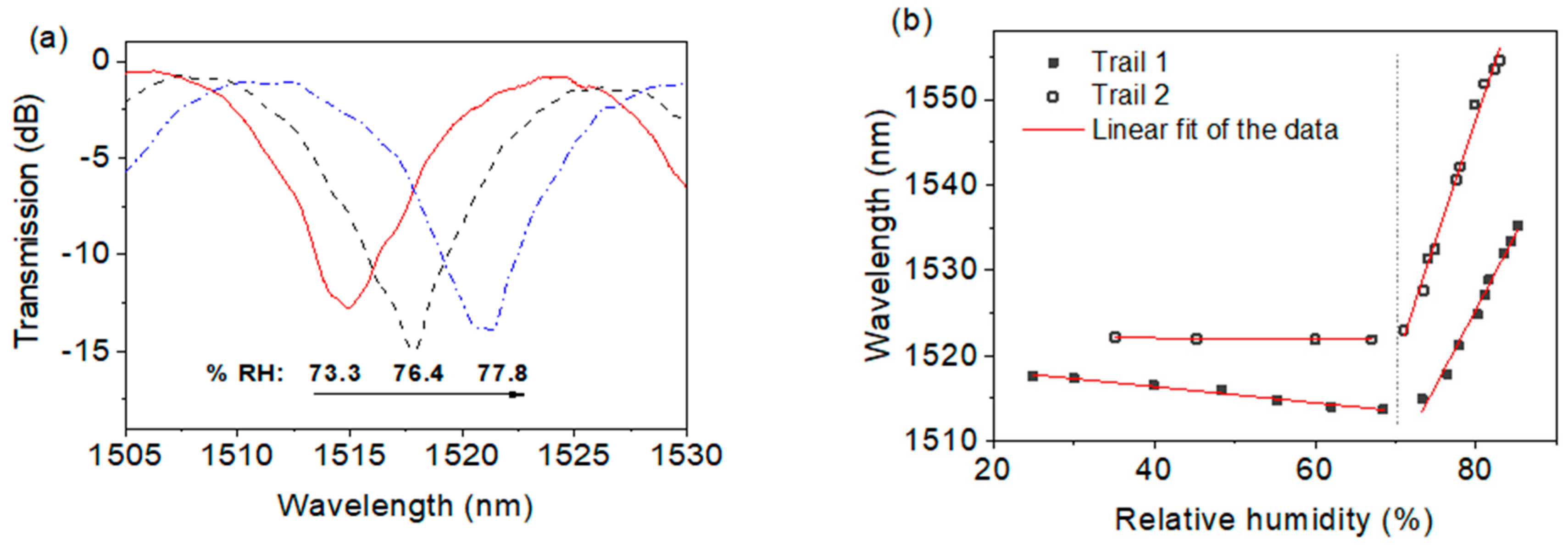
3.3. Humidity Sensor
3.4. Biosensor
3.5. Sensor Interrogation
4. Conclusions and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Grattan, K.T.V.; Sun, T. Fiber optic sensor technology: An overview. Sens. Actuators A Phys. 2000, 82, 40–61. [Google Scholar] [CrossRef]
- Othonos, A. Fiber Bragg gratings. Rev. Sci. Instrum. 1997, 68, 4309–4341. [Google Scholar] [CrossRef]
- Bhatia, V.; Vengsarkar, A.M. Optical fiber long-period grating sensors. Opt. Lett. 1996, 21, 692–694. [Google Scholar] [CrossRef] [PubMed]
- Kersey, A.; Davis, M.A.; Patrick, H.J.; Leblanc, M.; Koo, K.P.; Askins, C.G.; Putnam, M.A.; Friebele, E.J. Fiber grating sensors. J. Lightwave Technol. 1997, 15, 1442–1463. [Google Scholar] [CrossRef]
- Markowski, K.; Jędrzejewski, K.; Marzęcki, M.; Osuch, T. Linearly chirped tapered fiber-Bragg-grating-based Fabry-Perot cavity and its application in simultaneous strain and temperature measurement. Opt. Lett. 2017, 42, 1464–1467. [Google Scholar] [CrossRef] [PubMed]
- Osuch, T.; Markowski, K.; Jędrzejewski, K. Fiber-Optic Strain Sensors Based on Linearly Chirped Tapered Fiber Bragg Gratings With Tailored Intrinsic Chirp. IEEE Sens. J. 2016, 16, 7508–7514. [Google Scholar] [CrossRef]
- Nakazawa, M. Photonic Crystal Fibers. Opt. Express 2008, 12, 1528–1539. [Google Scholar] [CrossRef]
- Urbanczyk, W.; Martynkien, T.; Szpulak, M.; Statkiewicz, G.; Olszewski, J.; Wojcik, J. Photonic crystal fibers for sensing applications. J. Sens. 2012, 5950, 260–269. [Google Scholar]
- Kim, H.; Kim, J.; Paek, U.C.; Lee, B.H.; Kim, K.T. Tunable photonic crystal fiber coupler based on a side-polishing technique. Opt. Lett. 2004, 29, 1194–1196. [Google Scholar] [CrossRef] [PubMed]
- Rifat, A.A.; Ahmed, R.; Yetisen, A.K.; Butt, H.; Sabouri, A.; Mahdiraji, G.A.; Yun, S.H.; Adikan, F.R.M. Photonic crystal fiber based plasmonic sensors. Sens. Actuators B Chem. 2017, 243, 311–325. [Google Scholar] [CrossRef]
- Tong, L.; Gattass, R.R.; Ashcom, J.B.; He, S.; Lou, J.; Shen, M.; Maxwell, I.; Mazur, E. Subwavelength-diameter silica wires for low-loss optical wave guiding. Nature 2003, 426, 816. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Wei, L.; Zhang, X.; Song, Y. Supercontinuum Generation in Tapered Fibers. In Proceedings of the Communications and Photonics Conference and Exhibition, Shanghai, China, 2–6 November 2009; p. 71. [Google Scholar]
- Lissillour, F.; Messager, D.; Stephan, G.; Feron, P. Whispering-gallery-mode laser at 1.56 μm excited by a fiber taper. Opt. Lett. 2001, 26, 1051–1053. [Google Scholar] [CrossRef] [PubMed]
- Wei, P.K.; Tai, Y.H. Sensitive liquid refractive index sensors using tapered optical fiber tips. Opt. Lett. 2010, 35, 944–946. [Google Scholar]
- Birks, T.A.; Li, Y.W. The shape of fiber tapers. J. Lightwave Technol. 1992, 10, 432–438. [Google Scholar] [CrossRef]
- Brambilla, G.; Koizumi, F.; Feng, X.; Richardson, D.J. Compound-glass optical nanowires. Electron. Lett. 2005, 41, 400–402. [Google Scholar] [CrossRef]
- Lu, D.; Belacel, C.; Ducci, S.; Leo, G.; Favero, I. Ultralow loss single-mode silica tapers manufactured by a microheater. Appl. Opt. 2010, 49, 2441–2445. [Google Scholar]
- Wang, P.; Ding, M.; Bo, L.; Guan, C.; Semenova, Y.; Wu, Q.; Farrell, G.; Brambilla, G. Fiber-tip high-temperature sensor based on multimode interference. Opt. Lett. 2013, 38, 4617–4620. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Farrell, G.; Yan, W. Investigation on Single-Mode–Multimode–Single-Mode Fiber Structure. J. Lightwave Technol. 2008, 26, 512–519. [Google Scholar] [CrossRef]
- Wu, Q.; Semenova, Y.; Wang, P.; Farrell, G. High sensitivity SMS fiber structure based refractometer—Analysis and experiment. Opt. Express 2011, 19, 7937–7944. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Hatta, A.M.; Wang, P.; Semenova, Y.; Farrell, G. Use of a Bent Single SMS Fiber Structure for Simultaneous Measurement of Displacement and Temperature Sensing. IEEE Photonics Technol. Lett. 2011, 23, 130–132. [Google Scholar] [CrossRef]
- Wang, X.; Lewis, E.; Wang, P. Investigation of the self-imaging position of a singlemode-multimode-singlemode optical fiber structure. Microw. Opt. Technol. Lett. 2017, 59, 1645–1651. [Google Scholar] [CrossRef]
- Machavaram, V.R.; Badcock, R.A.; Fernando, G.F. Fabrication of intrinsic fibre Fabry-Perot sensors in silica fibres using hydrofluoric acid etching. Sens. Actuators A Phys. 2007, 138, 248–260. [Google Scholar] [CrossRef]
- Tseng, S.M.; Chen, C.L. Side-polished fibers. Appl. Opt. 1992, 31, 3438–3447. [Google Scholar] [CrossRef] [PubMed]
- Tian, Z.; Yam, S.H.; Loock, H.P. Single-Mode Fiber Refractive Index Sensor Based on Core-Offset Attenuators. IEEE Photonics Technol. Lett. 2008, 20, 1387–1389. [Google Scholar] [CrossRef]
- Hayashi, T.; Taru, T.; Shimakawa, O.; Sasaki, T.; Sasaoka, E. Low-Crosstalk and Low-Loss Multi-Core Fiber Utilizing Fiber Bend. In Proceedings of the Optical Fiber Communication Conference and Exposition, Los Angeles, CA, USA, 6–10 March 2011; pp. 1–3. [Google Scholar]
- Wang, P.; Brambilla, G.; Ding, M.; Semenova, Y.; Wu, Q.; Farrell, G. Investigation of single-mode–multimode–single-mode and single-mode–tapered-multimode–single-mode fiber structures and their application for refractive index sensing. J. Opt. Soc. Am. B 2011, 28, 1180–1186. [Google Scholar] [CrossRef]
- Sharma, A.; Agrawal, A. Wide angle beam propagation methods. Available online: https://www.researchgate.net/profile/Arti_Agrawal3/publication/228541190_WIDE_ANGLE_BEAM_PROPAGATION_METHODS/links/5595025708ae21086d1f036a.pdf (accessed on 12 March 2018).
- Hadley, G.R. Wide-angle beam propagation using Padé approximant operators. Opt. Lett. 1992, 17, 1426–1428. [Google Scholar] [CrossRef] [PubMed]
- Hadley, G.R. Multistep method for wide-angle beam propagation. Opt. Lett. 1992, 17, 1743–1745. [Google Scholar] [CrossRef] [PubMed]
- Flannery, B.P.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 1986; pp. 120–122. [Google Scholar]
- James, S.W.; Tatam, R.P. Optical fibre long-period grating sensors: Characteristics and application. Meas. Sci. Technol. 2003, 14, R49. [Google Scholar] [CrossRef]
- Melngailis, J. Focused ion beam technology and applications. J. Vac. Sci. Technol. B Microelectron. Process. Phenom. 1987, 5, 469–495. [Google Scholar] [CrossRef]
- Stewart, D.K.; Doyle, A.F.; Casey, J.D. Focused ion beam deposition of new materials: Dielectric films for device modification and mask repair and tantalum films for X-ray mask repair. Proc. SPIE Int. Soc. Opt. Eng. 1995, 2437, 276–283. [Google Scholar]
- Reyntjens, S.; Puers, R. A review of focused ion beam applications in microsystem technology. J. Micromech. Microeng. 2001, 11, 287–300. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Z.; Jian, S. Multimode interference refractive index sensor based on coreless fiber. Photonic Sens. 2014, 4, 21–27. [Google Scholar] [CrossRef]
- Wu, Q.; Semenova, Y.; Wang, P.; Farrell, G. A comprehensive analysis verified by experiment of a refractometer based on an SMF28-small-core singlemode fiber (SCSMF)–SMF28 fiber structure. J. Opt. 2011, 13, 125401. [Google Scholar] [CrossRef]
- Zhu, B.; Monberg, E.M.; Dimarcello, F.V.; Fini, J.M.; Fishteyn, M.; Yan, M.F.; Taunay, T.F. Seven-core multicore fiber transmissions for passive optical network. Opt. Express 2010, 18, 11117–11122. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Brambilla, G.; Ding, M.; Lee, T.; Bo, L.; Semenova, Y.; Wu, Q.; Farrell, G. Enhanced Refractometer Based on Periodically Tapered Small Core Singlemode Fiber. IEEE Sens. J. 2013, 13, 180–185. [Google Scholar] [CrossRef]
- Xia, T.H.; Zhang, A.P.; Gu, B.; Zhu, J.J. Fiber-optic refractive-index sensors based on transmissive and reflective thin-core fiber modal interferometers. Opt. Commun. 2010, 283, 2136–2139. [Google Scholar] [CrossRef]
- Gu, B.; Yin, M.; Zhang, A.P.; Qian, J.; He, S. Optical fiber relative humidity sensor based on FBG incorporated thin-core fiber modal interferometer. Opt. Express 2011, 19, 4140–4146. [Google Scholar] [CrossRef] [PubMed]
- Snyder, A.W.; Love, J.D. Optical Waveguide Theory; Chapman and Hall: London, UK, 1983; pp. 1–37. [Google Scholar]
- Bobb, L.C.; Shankar, P.M.; Krumboltz, H.D. Bending effects in biconically tapered single-mode fibers. J. Lightwave Technol. 1990, 8, 1084–1090. [Google Scholar] [CrossRef]
- Monerie, M. Propagation in doubly clad single-mode fibers. IEEE J. Quantum Electron. 2003, 18, 535–542. [Google Scholar] [CrossRef]
- Cutter, M.A. Planar Optical Waveguides and Fibres. Phys. Today 1979, 32, 51–54. [Google Scholar] [CrossRef]
- Farrell, G.; Zheng, J.; Wang, P.; Wu, Q.; Semenova, Y.; Ti, Y. Macrobending single-mode fiber-based refractometer. Appl. Opt. 2009, 48, 6044–6049. [Google Scholar]
- Davis, D.D.; Gaylord, T.K. Long-period fibre grating fabrication with focused CO2 laser pulses. Electron. Lett. 1998, 34, 302–303. [Google Scholar] [CrossRef]
- Tan, K.M.; Tay, C.M.; Tjin, S.C.; Chan, C.C.; Rahardjo, H. High relative humidity measurements using gelatin coated long-period grating sensors. Sens. Actuators B Chem. 2005, 110, 335–341. [Google Scholar] [CrossRef]
- Vengsarkar, A.M.; Lemaire, P.J.; Judkins, J.B.; Bhatia, B.; Erdogan, T.; Sipe, J.E. Long-period fiber gratings as band-rejection filters. J. Lightwave Technol. 2002, 14, 58–65. [Google Scholar] [CrossRef]
- Vengsarkar, A.M.; Pedrazzani, J.R.; Judkins, J.B.; Lemaire, P.J.; Bergano, N.S.; Davidson, C.R. Long-period fiber-grating-based gain equalizers. Opt. Lett. 1996, 21, 336–338. [Google Scholar] [CrossRef] [PubMed]
- Oh, S.; Lee, K.R.; Paek, U.C.; Chung, Y. Fabrication of helical long-period fiber gratings by useof a CO2 laser. Opt. Lett. 2004, 29, 1464–1466. [Google Scholar] [CrossRef] [PubMed]
- Davis, D.D.; Gaylord, T.K.; Glytsis, E.N.; Mettler, S.C. CO2 laser-induced long-period fibre gratings: Spectral characteristics, cladding modes and polarisation independence. Electron. Lett. 1998, 34, 1416–1417. [Google Scholar] [CrossRef]
- Davis, D.D.; Gaylord, T.K. Very-high-temperature stable CO2-laser-induced long-period fibre gratings. Electron. Lett. 2002, 35, 740–742. [Google Scholar] [CrossRef]
- Wang, P.; Brambilla, G.; Ding, M.; Semenova, Y.; Wu, Q.; Farrell, G. High-sensitivity, evanescent field refractometric sensor based on a tapered, multimode fiber interference. Opt. Lett. 2011, 36, 2233–2235. [Google Scholar] [CrossRef] [PubMed]
- Knight, J.C.; Birks, T.A.; Russell, P.S.; Atkin, D.M. All-silica single-mode optical fiber with photonic crystal cladding. Opt. Lett. 1996, 21, 1547–1549. [Google Scholar] [CrossRef] [PubMed]
- Cregan, R.F.; Mangan, B.J.; Knight, J.C.; Birks, T.A.; Russell, P.S.; Roberts, P.J.; Allan, D.C. Single-Mode Photonic Band Gap Guidance of Light in Air. Science 1999, 285, 1537–1539. [Google Scholar] [CrossRef] [PubMed]
- Kumar, V.R.K.; George, A.K.; Reeves, W.H.; Knight, J.C.; Russell, P.S.J.; Omenetto, F.G.; Taylor, A.J. Extruded soft glass photonic crystal fiber for ultrabroad supercontinuum generation. Opt. Express 2002, 10, 1520–1525. [Google Scholar] [CrossRef] [PubMed]
- Dudley, J.M.; Taylor, J.R. Ten years of nonlinear optics in photonic crystal fibre. Nat. Photonics 2009, 3, 85–90. [Google Scholar] [CrossRef]
- Limpert, J.; Schreiber, T.; Nolte, S.; Zellmer, H.; Tünnermann, A.; Iliew, R.; Lederer, F.; Broeng, J.; Vienne, G.; Petersson, A. High-power air-clad large-mode-area photonic crystal fiber laser. Opt. Express 2003, 11, 818–823. [Google Scholar] [CrossRef] [PubMed]
- Dudley, J.M.; Genty, G.; Coen, S. Supercontinuum generation in photonic crystal fiber. Rev. Mod. Phys. 2006, 78, 1135–1184. [Google Scholar] [CrossRef]
- Li, P.; Shi, K.; Liu, Z. Manipulation and spectroscopy of a single particle by use of white-light optical tweezers. Opt. Lett. 2005, 30, 156–158. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.K.C.; Kuhlmey, B.T.; Eggleton, B.J. Ultrasensitive photonic crystal fiber refractive index sensor. Opt. Lett. 2009, 34, 322–324. [Google Scholar] [CrossRef] [PubMed]
- Jensen, J.B.; Pedersen, L.H.; Hoiby, P.E.; Nielsen, L.B.; Hansen, T.P.; Folkenberg, J.R.; Riishede, J.; Noordegraaf, D.; Nielsen, K.F.; Carlsen, A. Photonic crystal fiber based evanescent-wave sensor for detection of biomolecules in aqueous solutions. Opt. Lett. 2004, 29, 1974–1976. [Google Scholar] [CrossRef] [PubMed]
- Haakestad, M.W.; Alkeskjold, T.T.; Nielsen, M.D.; Scolari, L.; Riishede, J.; Engan, H.E.; Bjarklev, A. Electrically tunable photonic bandgap guidance in a liquid-crystal-filled photonic crystal fiber. IEEE Photonics Technol. Lett. 2005, 17, 819–821. [Google Scholar] [CrossRef]
- Kakarantzas, G.; Birks, T.A.; Russell, P.S. Structural long-period gratings in photonic crystal fibers. Opt. Lett. 2002, 27, 1013–1015. [Google Scholar] [CrossRef] [PubMed]
- Wei, C.W.; Chan, C.C.; Chen, L.H.; Li, T.; Lee, K.X.; Leong, K.C. Polyvinyl alcohol coated photonic crystal optical fiber sensor for humidity measurement. Sens. Actuators B Chem. 2012, 174, 563–569. [Google Scholar]
- Rindorf, L.; Bang, O. Sensitivity of photonic crystal fiber grating sensors: Biosensing, refractive index, strain, and temperature sensing. J. Opt. Soc. Am. B 2007, 25, 310–324. [Google Scholar] [CrossRef]
- Lim, J.H.; Jang, H.S.; Lee, K.S.; Kim, J.C.; Lee, B.H. Mach-Zehnder interferometer formed in a photonic crystal fiber based on a pair of long-period fiber gratings. Opt. Lett. 2004, 29, 346–348. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.L.; Demokan, M.S.; Jin, W.; Xiao, L. A cheap and practical FBG temperature sensor utilizing a long-period grating in a photonic crystal fiber. Opt. Commun. 2007, 276, 242–245. [Google Scholar] [CrossRef]
- Zhu, Y.; He, Z.; Du, H. Detection of external refractive index change with high sensitivity using long-period gratings in photonic crystal fiber. Sens. Actuators B Chem. 2008, 131, 265–269. [Google Scholar] [CrossRef]
- Xiao, L.; Jin, W.; Demokan, M.S. Fusion splicing small-core photonic crystal fibers and single-mode fibers by repeated arc discharges. Opt. Lett. 2007, 32, 115–117. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Ding, M.; Bo, L.; Guan, C.; Semenova, Y.; Sun, W.; Yuan, L.; Brambilla, G.; Farrell, G. Photonic crystal fiber half-taper probe based refractometer. Opt. Lett. 2014, 39, 2076–2079. [Google Scholar] [CrossRef] [PubMed]
- Jung, Y.; Brambilla, G.; Richardson, D.J. Optical microfiber coupler for broadband single-mode operation. Opt. Express 2009, 17, 5273–5278. [Google Scholar] [CrossRef] [PubMed]
- Sulaiman, A.; Harun, S.W.; Muhammad, M.Z.; Ahmad, H. Compact Dual-Wavelength Laser Generation Using Highly Concentrated Erbium-Doped Fiber Loop Attached to Microfiber Coupler. IEEE J. Quantum Electron. 2013, 49, 586–588. [Google Scholar] [CrossRef]
- Chen, Y.; Yan, S.C.; Zheng, X.; Xu, F.; Lu, Y.Q. A miniature reflective micro-force sensor based on a microfiber coupler. Opt. Express 2014, 22, 2443–2450. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Xu, F.; Yan, S.; Lu, Y.; Chen, Y. Differential twin receiving fiber-optic magnetic field and electric current sensor utilizing a microfiber coupler. Opt. Express 2015, 23, 9407–9414. [Google Scholar]
- Jung, Y.; Brambilla, G.; Richardson, D.J. Broadband Single-Mode Microfiber Coupler for OCT. In Proceedings of the Conference on Optical Fiber Communication—Incudes Post Deadline Papers (OFC 2009), San Diego, CA, USA, 22–26 March 2009; pp. 1–3. [Google Scholar]
- Wang, P.; Semenova, Y.; Brambilla, G.; Farrell, G. An investigation of the polarization dependence of a temperature sensor based on an optical microfiber coupler. In Proceedings of the OFS2012 International Conference on Optical Fiber Sensor, Beijing, China, 14–19 October 2012; p. 84217Y. [Google Scholar]
- Richardson, D.J.; Brambilla, G.; Giles, I.P.; Chen, R.; Ismaeel, R.; Alam, S.U.; Jung, Y. Dual mode fused optical fiber couplers suitable for mode division multiplexed transmission. Opt. Express 2013, 21, 24326–24331. [Google Scholar]
- Sulaiman, A.; Harun, S.W.; Ahmad, H. Ring microfiber coupler erbium-doped fiber laser analysis. Chin. Opt. Lett. 2014, 12, 42–45. [Google Scholar] [CrossRef]
- Bo, L.; Wang, P.; Semenova, Y.; Farrell, G. High Sensitivity Fiber Refractometer Based on an Optical Microfiber Coupler. IEEE Photonics Technol. Lett. 2013, 25, 228–230. [Google Scholar] [CrossRef]
- Okamoto, K. Fundamentals of Optical Waveguides, 2nd ed.; Academic Press: Cambridge, MA, USA, 2006; pp. 535–554. [Google Scholar]
- Payne, F.P.; Hussey, C.D.; Yataki, M.S. Polarisation analysis of strongly fused and weakly fused tapered couplers. Electron. Lett. 1985, 21, 561–563. [Google Scholar] [CrossRef]
- Xu, F.; Horak, P.; Brambilla, G. Optimized Design of Microcoil Resonators. J. Lightwave Technol. 2007, 25, 1561–1567. [Google Scholar] [CrossRef]
- Sumetsky, M. Optical fiber microcoil resonators. Opt. Express 2004, 12, 2303–2316. [Google Scholar] [CrossRef] [PubMed]
- Tewari, R.; Thyagarajan, K. Analysis of tunable single-mode fiber directional couplers using simple and accurate relations. J. Lightwave Technol. 1986, 4, 386–390. [Google Scholar] [CrossRef]
- Brambilla, G.; Finazzi, V.; Richardson, D. Ultra-low-loss optical fiber nanotapers. Opt. Express 2004, 12, 2258–2263. [Google Scholar] [CrossRef] [PubMed]
- Ding, M.; Wang, P.; Brambilla, G. A microfiber coupler tip thermometer. Opt. Express 2012, 20, 5402–5408. [Google Scholar] [CrossRef] [PubMed]
- Ding, M.; Wang, P.; Brambilla, G. Fast-Response High-Temperature Microfiber Coupler Tip Thermometer. IEEE Photonics Technol. Lett. 2012, 24, 1209–1211. [Google Scholar] [CrossRef]
- Jasim, A.A.; Zulkifli, A.Z.; Muhammad, M.Z.; Harun, S.W.; Ahmad, H. A new compact micro-ball lens structure at the cleaved tip of microfiber coupler for displacement sensing. Sens. Actuators A Phys. 2013, 189, 177–181. [Google Scholar] [CrossRef]
- Polynkin, P.; Polynkin, A.; Peyghambarian, N.; Mansuripur, M. Evanescent field-based optical fiber sensing device for measuring the refractive index of liquids in microfluidic channels. Opt. Lett. 2005, 30, 1273–1275. [Google Scholar] [CrossRef] [PubMed]
- Villatoro, J.; Monzon-Hernandez, D.; Talavera, D. High resolution refractive index sensing with cladded multimode tapered optical fibre. Electron. Lett. 2004, 40, 106–107. [Google Scholar] [CrossRef]
- Tian, Z.; Yam, S.S.; Loock, H.P. Refractive index sensor based on an abrupt taper Michelson interferometer in a single-mode fiber. Opt. Lett. 2008, 33, 1105–1107. [Google Scholar] [CrossRef] [PubMed]
- Arregui, F.J.; Matias, I.R.; Corres, J.M. Design of Humidity Sensors Based on Tapered Optical Fibers. J. Lightwave Technol. 2006, 24, 4329–4336. [Google Scholar]
- Villatoro, J.; Luna-Moreno, D.; Monzón-Hernández, D. Optical fiber hydrogen sensor for concentrations below the lower explosive limit. Sens. Actuators B Chem. 2005, 110, 23–27. [Google Scholar] [CrossRef]
- Layeghi, A.; Latifi, H.; Frazao, O. Magnetic Field Sensor Based on Nonadiabatic Tapered Optical Fiber with Magnetic Fluid. IEEE Photonics Technol. Lett. 2014, 26, 1904–1907. [Google Scholar] [CrossRef]
- Corres, J.M.; Bravo, J.; Matias, I.R.; Arregui, F.J. Tapered optical fiber biosensor for the detection of anti-gliadin antibodies. Sens. Actuators B Chem. 2008, 135, 166–171. [Google Scholar] [CrossRef]
- Villatoro, J.; Minkovich, V.P.; Monzón-Hernández, D. Temperature-independent strain sensor made from tapered holey optical fiber. Opt. Lett. 2006, 31, 305–307. [Google Scholar] [CrossRef] [PubMed]
- Frazão, O.; Falate, R.; Fabris, J.L.; Santos, J.L.; Ferreira, L.A.; Araújo, F.M. Optical inclinometer based on a single long-period fiber grating combined with a fused taper. Opt. Lett. 2006, 31, 2960–2962. [Google Scholar] [CrossRef] [PubMed]
- Amaral, L.M.N.; Frazao, O.; Santos, J.L.; Ribeiro, A.B.L. Fiber-Optic Inclinometer Based on Taper Michelson Interferometer. IEEE Sens. J. 2011, 11, 1811–1814. [Google Scholar] [CrossRef]
- Osuch, T.; Markowski, K.; Jedrzejewski, K. Temperature Independent Tapered Fiber Bragg Grating-Based Inclinometer. IEEE Photonics Technol. Lett. 2015, 27, 2312–2315. [Google Scholar] [CrossRef]
- Iadicicco, A.; Cusano, A.; Cutolo, A.; Bernini, R. Thinned fiber Bragg gratings as high sensitivity refractive index sensor. IEEE Photonics Technol. Lett. 2004, 16, 1149–1151. [Google Scholar] [CrossRef]
- Liang, W.; Huang, Y.; Xu, Y.; Lee, R.K.; Yariv, A. Highly sensitive fiber Bragg grating refractive index sensors. Appl. Phys. Lett. 2005, 86, 151122. [Google Scholar] [CrossRef]
- Monzón-Hernández, D.; Villatoro, J. High-resolution refractive index sensing by means of a multiple-peak surface plasmon resonance optical fiber sensor. Sens. Actuators B Chem. 2006, 115, 227–231. [Google Scholar] [CrossRef]
- Finlan, M.F.; Brady, M.A.W. Surface Plasmon Resonance Sensors. US Patent US5035863A, 30 July 1991. [Google Scholar]
- Priya, B.; Gupta, B.D. Surface-plasmon-resonance-based fiber-optic refractive index sensor: Sensitivity enhancement. Appl. Opt. 2011, 50, 2032–2036. [Google Scholar]
- Xue, L.L.; Yang, L. Sensitivity Enhancement of RI Sensor Based on SMS Fiber Structure with High Refractive Index Overlay. J. Lightwave Technol. 2012, 30, 1463–1469. [Google Scholar]
- Yadav, T.; Narayanaswamy, R.; Bakar, M.A.; Kamil, Y.M.; Mahdi, M. Single mode tapered fiber-optic interferometer based refractive index sensor and its application to protein sensing. Opt. Express 2014, 22, 22802–22807. [Google Scholar] [CrossRef] [PubMed]
- Yan, B.; Yu, C.; Farrell, G.; Wang, P.; Wu, Q.; Ma, Y.; Semenova, Y. Fiber refractometer based on a fiber Bragg grating and single-mode–multimode–single-mode fiber structure. Opt. Lett. 2011, 36, 2197–2199. [Google Scholar]
- Wang, P.; Bo, L.; Guan, C.; Semenova, Y.; Wu, Q.; Brambilla, G.; Farrell, G. Low-temperature sensitivity periodically tapered photonic crystal-fiber-based refractometer. Opt. Lett. 2013, 38, 3795–3798. [Google Scholar] [CrossRef] [PubMed]
- Rao, Y.J. In-fibre Bragg grating sensors. Meas. Sci. Technol. 1997, 8, 355. [Google Scholar] [CrossRef]
- Udd, E. Fiber Optic Bragg Grating Sensors. Proc. SPIE 1990, 1169, 98–107. [Google Scholar]
- Jung, J.; Nam, H.; Lee, B.; Byun, J.O.; Kim, N.S. Fiber Bragg grating temperature sensor with controllable sensitivity. In Proceedings of the Lasers and Electro-Optics Society Meeting (LEOS ’98), Orlando, FL, USA, 1–4 December 1998; Volume 1, pp. 405–406. [Google Scholar]
- Bhatia, V. Applications of long-period gratings to single and multi-parameter sensing. Opt. Express 1999, 4, 457–466. [Google Scholar] [CrossRef] [PubMed]
- Hall, B.D. Enhanced sensitivity fibre optic long period grating temperature sensor. Meas. Sci. Technol. 2002, 13, 792–795. [Google Scholar]
- Lee, C.E.; Taylor, H.F.; Markus, A.M.; Udd, E. Optical-fiber Fabry-Perot embedded sensor. Opt. Lett. 1989, 14, 1225–1227. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.E.; Taylor, H.F. Fiber-optic Fabry-Perot temperature sensor using a low-coherence light source. J. Lightwave Technol. 1991, 9, 129–134. [Google Scholar] [CrossRef]
- Starodumov, A.N.; Zenteno, L.A.; Monzon, D.; De La Rosa, E. Fiber Sagnac interferometer temperature sensor. Appl. Phys. Lett. 1997, 70, 19–21. [Google Scholar] [CrossRef]
- Tripathi, S.M.; Kumar, A.; Varshney, R.K.; Kumar, Y.B.P.; Marin, E.; Meunier, J.-P. Strain and temperature sensing characteristics of single-mode–multimode–single-mode structures. J. Lightwave Technol. 2009, 27, 2348–2356. [Google Scholar] [CrossRef]
- Yeo, T.L.; Sun, T.; Grattan, K.T.V.; Parry, D.; Lade, R.; Powell, B.D. Characterisation of a polymer-coated fibre Bragg grating sensor for relative humidity sensing. Sens. Actuators B Chem. 2005, 110, 148–156. [Google Scholar] [CrossRef]
- Konstantaki, M.; Madamopoulos, N.; Vainos, N.A.; Pissadakis, S.; Pispas, S. Optical fiber long-period grating humidity sensor with poly(ethylene oxide)/cobalt chloride coating. Appl. Opt. 2006, 45, 4567–4571. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Gu, F.; Lou, J.; Yin, X.; Tong, L. Fast detection of humidity with a subwavelength-diameter fiber taper coated with gelatin film. Opt. Express 2008, 16, 13349–13353. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Dong, X.; Chan, C.C.; Ni, K.; Zhang, S.; Shum, P.P. Humidity Sensor With a PVA-Coated Photonic Crystal Fiber Interferometer. IEEE Sens. J. 2013, 13, 2214–2216. [Google Scholar] [CrossRef]
- Bo, L.; Wang, P.; Semenova, Y.; Farrell, G. Optical microfiber coupler based humidity sensor with a polyethylene oxide coating. Microw. Opt. Technol. Lett. 2015, 57, 457–460. [Google Scholar] [CrossRef]
- Acikgoz, S.; Bilen, B.; Demir, M.M.; Menceloglu, Y.Z.; Skarlatos, Y.; Aktas, G.; Inci, M.N. Use of polyethylene glycol coatings for optical fibre humidity sensing. Opt. Rev. 2008, 15, 84. [Google Scholar] [CrossRef] [Green Version]
- Bownass, D.C.; Barton, J.S.; Jones, J.D.C. Detection of high humidity by optical fibre sensing at telecommunications wavelengths. Opt. Commun. 1998, 146, 90–94. [Google Scholar] [CrossRef]
- Stuart, M.C.; Fleer, G.; Bijsterbosch, B. The adsorption of poly (vinyl pyrrolidone) onto silica. I. Adsorbed amount. J. Colloid Interface Sci. 1982, 90, 310–320. [Google Scholar] [CrossRef]
- Thévenot, D.R.; Toth, K.; Durst, R.A.; Wilson, G.S. Electrochemical biosensors: Recommended definitions and classification. Biosens. Bioelectron. 2001, 16, 121–131. [Google Scholar] [CrossRef]
- Fan, X.; White, I.M.; Shopova, S.I.; Zhu, H.; Suter, J.D.; Sun, Y. Sensitive optical biosensors for unlabeled targets: A review. Anal. Chim. Acta 2008, 620, 8–26. [Google Scholar] [CrossRef] [PubMed]
- Abel, A.P.; Weller, M.G.; Duveneck, G.L.; Ehrat, M.; Widmer, H.M. Fiber-Optic Evanescent Wave Biosensor for the Detection of Oligonucleotides. Anal. Chem. 1996, 68, 2905–2912. [Google Scholar] [CrossRef] [PubMed]
- Bosch, M.E.; Sánchez, A.J.R.; Rojas, F.S.; Ojeda, C.B. Recent Development in Optical Fiber Biosensors. Sensors 2007, 7, 797–859. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, W.; Wu, N.; Zou, X.; Wang, X. Tapered Optical Fiber Sensor for Label-Free Detection of Biomolecules. Sensors 2011, 11, 3780–3790. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Bo, L.; Semenova, Y.; Farrell, G.; Brambilla, G. Optical Microfibre Based Photonic Components and Their Applications in Label-Free Biosensing. Biosensors 2015, 5, 471–499. [Google Scholar] [CrossRef] [PubMed]
- Lamont, R.G.; Johnson, D.C.; Hill, K.O. Power transfer in fused biconical-taper single-mode fiber couplers: Dependence on external refractive index. Appl. Opt. 1985, 24, 327–332. [Google Scholar] [CrossRef] [PubMed]
- Bo, L.; O’Mahony, C.C.; Semenova, Y.; Gilmartin, N.; Wang, P.; Farrell, G. Microfiber coupler based label-free immunosensor. Opt. Express 2014, 22, 8150–8155. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Farrell, G.; Freir, T. Study of transmission response of edge filters employed in wavelength measurements. Appl. Opt. 2005, 44, 7789–7792. [Google Scholar] [CrossRef] [PubMed]
- Rajan, G.; Wang, Q.; Farrell, G.; Semenova, Y.; Wang, P. Effect of SNR of input signal on the accuracy of a ratiometric wavelength measurement system. Microw. Opt. Technol. Lett. 2007, 49, 1022–1024. [Google Scholar] [CrossRef]
- Wang, Q.; Farrell, G.; Freir, T.; Rajan, G.; Wang, P. Low-cost wavelength measurement based on a macrobending single-mode fiber. Opt. Lett. 2006, 31, 1785–1787. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Brambilla, G.; Ding, M.; Semenova, Y.; Wu, Q.; Farrell, G. The Use of a Fiber Comb Filter Fabricated by a CO2 Laser Irradiation to Improve the Resolution of a Ratiometric Wavelength Measurement System. J. Lightwave Technol. 2012, 30, 1143–1149. [Google Scholar] [CrossRef]

























| Fiber Structure | RI Range | Average Sensitivity | Maximum Sensitivity | Resolution | Temperature Dependence |
|---|---|---|---|---|---|
| STMS | 1.33–1.44 | 487 nm/RIU | 1913 nm/RIU | 5.23 × 10−6 | |
| SPTS | 1.33–1.38 | 226.6 nm/RIU | 383 nm/RIU | 4.41 × 10−5 | 0.13 nm/°C |
| SPS | 1.33–1.38 | 222 nm/RIU | 232 nm/RIU | 3.24 × 10−5 | 8.4 pm/°C |
| SPST | 1.33–1.38 | 39.1 nm/RIU | 2.56 × 10−4 | 7.67 pm/°C | |
| FIB-milled gold coated SMST | 1.33–1.40 | 265 nm/RIU | 3.77 × 10−5 | ||
| MFC | 1.3340–1.3800 | 2723 nm/RIU | 4155 nm/RIU | 3.67 × 10−5 |
| Fiber Structure | Temperature Range | Average Sensitivity | Resolution | Response |
|---|---|---|---|---|
| MMF tip | 20–1089 °C | 11.4 pm/°C | 0.877 °C | |
| MFC tip | 85–1511 °C | 1.514 × 10−3 dB/°C | 0.66 °C | 16.6 ms |
| MFC | 701–1029 °C | 36.59 pm/°C |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Zhao, H.; Wang, X.; Farrell, G.; Brambilla, G. A Review of Multimode Interference in Tapered Optical Fibers and Related Applications. Sensors 2018, 18, 858. https://doi.org/10.3390/s18030858
Wang P, Zhao H, Wang X, Farrell G, Brambilla G. A Review of Multimode Interference in Tapered Optical Fibers and Related Applications. Sensors. 2018; 18(3):858. https://doi.org/10.3390/s18030858
Chicago/Turabian StyleWang, Pengfei, Haiyan Zhao, Xianfan Wang, Gerald Farrell, and Gilberto Brambilla. 2018. "A Review of Multimode Interference in Tapered Optical Fibers and Related Applications" Sensors 18, no. 3: 858. https://doi.org/10.3390/s18030858
APA StyleWang, P., Zhao, H., Wang, X., Farrell, G., & Brambilla, G. (2018). A Review of Multimode Interference in Tapered Optical Fibers and Related Applications. Sensors, 18(3), 858. https://doi.org/10.3390/s18030858





