A Compact Microwave Microfluidic Sensor Using a Re-Entrant Cavity
Abstract
1. Introduction
2. Theory
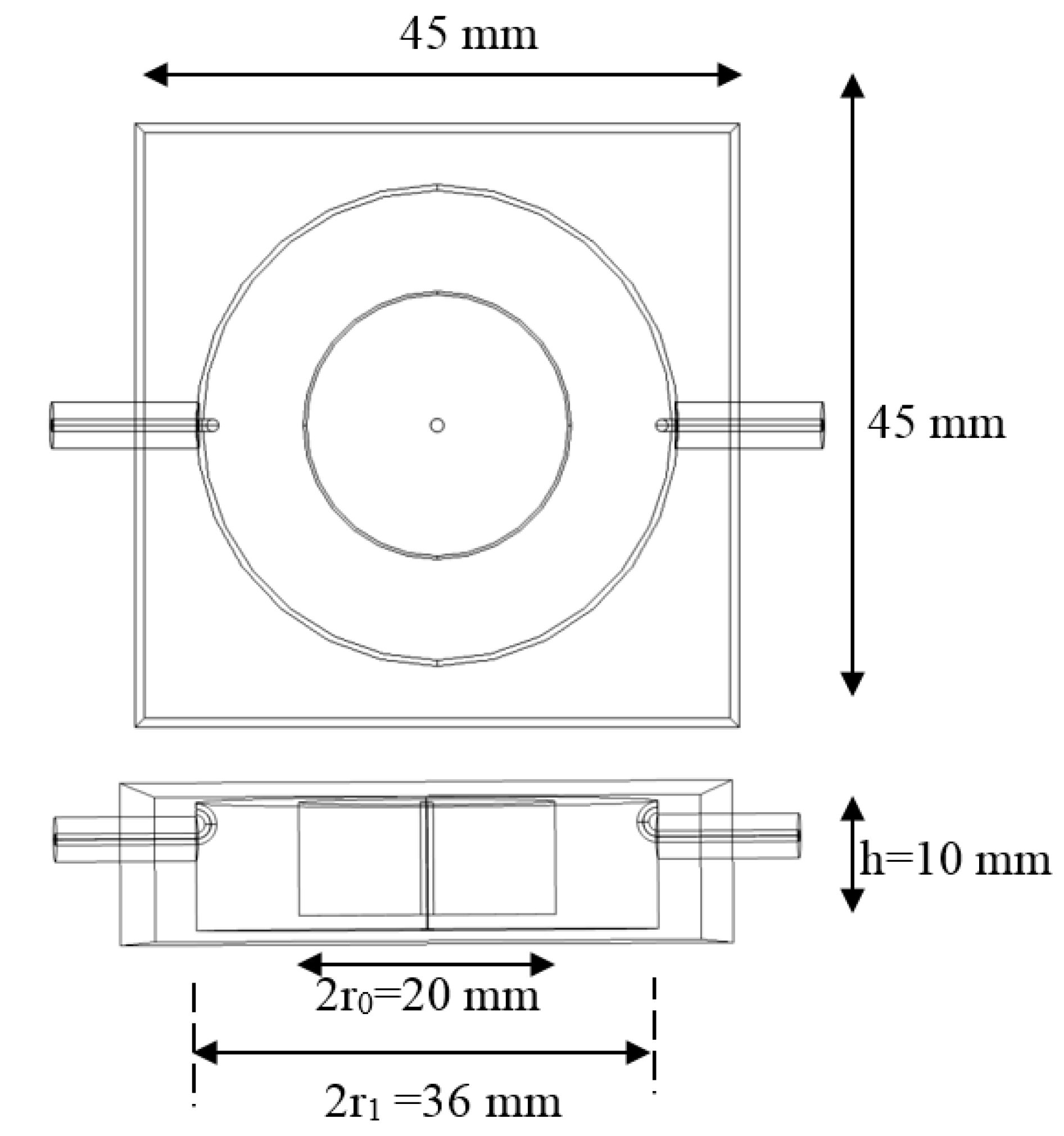
3. Cavity Design and Fabrication
- The electric field is parallel to the sample length, meaning that depolarization is minimal and the changes in resonator parameters (such as resonant frequency) are linearly dependent on the relative permittivity.
- The effective volume of the re-entrant cavity is very small, yielding a sensitive sample characterization.
4. Microfluidic System Design
5. Results
5.1. Simulation Results
5.2. Experimental Results
5.3. Results for Segments Flow
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Zhao, Y.; Li, Y.; Pan, B.; Kim, S.-H.; Liu, Z.; Tentzeris, M.M.; Papapolymerou, J.; Allen, M.G. RF evanescent-mode cavity resonator for passive wireless sensor applications. Sens. Actuators A Phys. 2010, 161, 322–328. [Google Scholar] [CrossRef]
- Elbuken, C.; Glawdel, T.; Chan, D.; Ren, C.L. Detection of microdroplet size and speed using capacitive sensors. Sens. Actuators A Phys. 2011, 171, 55–62. [Google Scholar] [CrossRef]
- Chretiennot, T.; Dubuc, D.; Grenier, K. A microwave and microfluidic planar resonator for efficient and accurate complex permittivity characterization of aqueous solutions. IEEE Trans. Microw. Theory Tech. 2013, 61, 972–978. [Google Scholar] [CrossRef]
- Yu, K.B.; Ogourtsov, S.G.; Belenky, V.G.; Maslenikov, A.B.; Omar, A.S. Accurate microwave resonant method for complex permittivity measurements of liquids. IEEE Trans. Microw. Theory Tech. 2000, 48, 2159–2164. [Google Scholar]
- Krupka, J.; Breeze, J.; Centeno, A.; Alford, N.; Claussen, T.; Jensen, L. Measurements of permittivity, dielectric loss tangent, and resistivity of float-zone silicon at microwave frequencies. IEEE Trans. Microw. Theory Tech. 2006, 54, 3995–4001. [Google Scholar] [CrossRef]
- Bonde, S.; D’Silva, R.; Gupte, V.; John, M.; Fernandes, F.; Kotrashetti, A. 2.4 GHz cavity notch filter for UWB radio. In Proceedings of the 2011 Annual IEEE India Conference (INDICON), Hyderabad, India, 16–18 December 2011; pp. 1–4. [Google Scholar]
- Pandit, H.; Shi, D.; Babu, N.H.; Chaud, X.; Cardwell, D.A.; He, P.; Isfort, D.; Tournier, R.; Mast, D.; Ferendeci, A.M. High Tc superconductor re-entrant cavity filter structures. Phys. C Supercond. 2005, 425, 44–51. [Google Scholar] [CrossRef]
- Krupka, J.; Geyer, R.G.; Baker-Jarvis, J.; Ceremuga, J. Measurements of the complex permittivity of microwave circuit board substrates using split dielectric resonator and reentrant cavity techniques. In Proceedings of the Seventh International Conference on Dielectric Materials, Measurements and Applications, Bath, UK, 23–26 September 1996; pp. 21–24. [Google Scholar]
- Harrington, R.D.; Powell, R.C.; Haas, P.H. A re-entrant cavity for measurement of complex permeability in the very-high-frequency region. Res. Natl. Bur. Stand. 1956, 56, 129–134. [Google Scholar] [CrossRef]
- Shindo, Y.; Kato, K.; Tsuchiya, K.; Yabuhara, T.; Shigihara, T.; Iwazaki, R.; Uzuka, T.; Takahashi, H. Heating properties of re-entrant resonant applicator for brain tumor by electromagnetic heating modes. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; pp. 3609–3612. [Google Scholar]
- Ishihara, Y.; Endo, Y.; Ohwada, H.; Wadamori, N. Noninvasive thermometry in a reentrant resonant cavity applicator. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; pp. 1487–1490. [Google Scholar]
- Barroso, J.J.; Castro, P.J.; Neto, J.P.L.; Aguiar, O.D. Reentrant cylindrical cavities. In Proceedings of the 2005 SBMO/IEEE MTT-S International Conference on Microwave and Optoelectronics, Brasilia, Brazil, 25 July 2005; pp. 129–132. [Google Scholar]
- Sheen, J. Microwave measurements of dielectric properties using a closed cylindrical cavity dielectric resonator. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 1139–1144. [Google Scholar] [CrossRef]
- Li, S.; Akyel, C.; Bosisio, R.G. Precise Calculations and Measurements on the complex dielectric constant of lossy materials using TM010 cavity perturbation techniques. IEEE Trans. Microw. Theory Tech. 1981, 29, 1041–1048. [Google Scholar]
- Verma, A.; Dube, D.C. Measurement of dielectric parameters of small samples at X-band frequencies by cavity perturbation technique. IEEE Trans. Instrum. Meas. 2005, 54, 2120–2123. [Google Scholar] [CrossRef]
- Abduljabar, A.A.; Rowe, D.J.; Porch, A.; Barrow, D.A. Novel microwave microfluidic sensor using a microstrip split-ring resonator. IEEE Trans. Microw. Theory Tech. 2014, 62, 679–688. [Google Scholar] [CrossRef]
- Morgan, A.J.L.; Naylon, J.; Gooding, S.; John, C.; Squires, O.; Lees, J.; Barrow, D.A.; Porch, A. Efficient microwave heating of microfluidic systems. Sens. Actuators B Chem. 2013, 181, 904–909. [Google Scholar] [CrossRef]
- Khan, A.S. Microwave Engineering Concepts and Fundamentals; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Zhang, K.; Li, D. Electromagnetic Theory for Microwaves and Optpelectronics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1998. [Google Scholar]
- Fujisawa, K. General treatment of klystron resonant cavities. IRE Trans. Microw. Theory Tech. 1958, 6, 344–358. [Google Scholar] [CrossRef]
- Raptis, A.C.; Lonngren, K.E. Microwave cavities for plasma diagnostics. J. Microw. Power Electromagn. Energy 1969, 4, 182–187. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Collin, R.E. Field Theory of Guided Waves; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1960. [Google Scholar]
- Engtsson, N.E.; Ohlsson, T. Microwave heating in the food industry. Proc. IEEE 1974, 62, 44–55. [Google Scholar] [CrossRef]
- Das, S.; Mukhopadhyay, A.K.; Datta, S.; Basu, D. Prospects of microwave processing: An overview. Bull. Mater. Sci. 2009, 32, 943–956. [Google Scholar] [CrossRef]












| Resonator | |||
|---|---|---|---|
| Water | 78.4 | 5.16 | 8.27 |
| Methanol | 32.5 | 5.60 | 51.5 |
| Ethanol | 24.3 | 4.20 | 163 |
| Chloroform | 4.72 | 2.50 | 7.96 |
| Resonator | Simulated fr (GHz) | Measured fr (GHz) | Simulated Quality | Measured Quality | Simulated IL (dB) | Measured IL (dB) | Simulated Permittivity | Measured Permittivity | Error |
|---|---|---|---|---|---|---|---|---|---|
| Empty | 2.4271 | 2.4271 | 1190 | 1187 | −25.020 | −25.153 | |||
| Water | 2.4161 | 2.4160 | 615 | 613 | −31.527 | −31.578 | 77.23 − j9.04 | 77.85 − j9.10 | 0.8% |
| Methanol | 2.4229 | 2.4227 | 385 | 381 | −35.509 | −35.296 | 22.27 − j13.06 | 22.84 − j12.87 | 1.5% |
| Ethanol | 2.4257 | 2.4255 | 483 | 480 | −33.169 | −33.117 | 7.01 − j6.97 | 7.27 − j6.96 | 1.7% |
| Chloroform | 2.4263 | 2.4261 | 1125 | 1125 | −25.557 | −25.663 | 4.69 −d j0.27 | 4.81 − j0.30 | 2.5% |
| Segment Type | Velocity (mm/sec.) Measured by Camera | Length (mm) from Camera | Length (mm) from Cavity |
|---|---|---|---|
| Water | 3.4 ± 0.2 | 18.5 ± 1.2 | 18.2 ± 0.9 |
| Oil | 3.4 ± 0.2 | 35.5 ± 1.2 | 33.6 ± 1.6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamzah, H.; Abduljabar, A.; Lees, J.; Porch, A. A Compact Microwave Microfluidic Sensor Using a Re-Entrant Cavity. Sensors 2018, 18, 910. https://doi.org/10.3390/s18030910
Hamzah H, Abduljabar A, Lees J, Porch A. A Compact Microwave Microfluidic Sensor Using a Re-Entrant Cavity. Sensors. 2018; 18(3):910. https://doi.org/10.3390/s18030910
Chicago/Turabian StyleHamzah, Hayder, Ali Abduljabar, Jonathan Lees, and Adrian Porch. 2018. "A Compact Microwave Microfluidic Sensor Using a Re-Entrant Cavity" Sensors 18, no. 3: 910. https://doi.org/10.3390/s18030910
APA StyleHamzah, H., Abduljabar, A., Lees, J., & Porch, A. (2018). A Compact Microwave Microfluidic Sensor Using a Re-Entrant Cavity. Sensors, 18(3), 910. https://doi.org/10.3390/s18030910





