A Monolithic Electrochemical Micro Seismic Sensor Capable of Monitoring Three-Dimensional Vibrations
Abstract
:1. Introduction
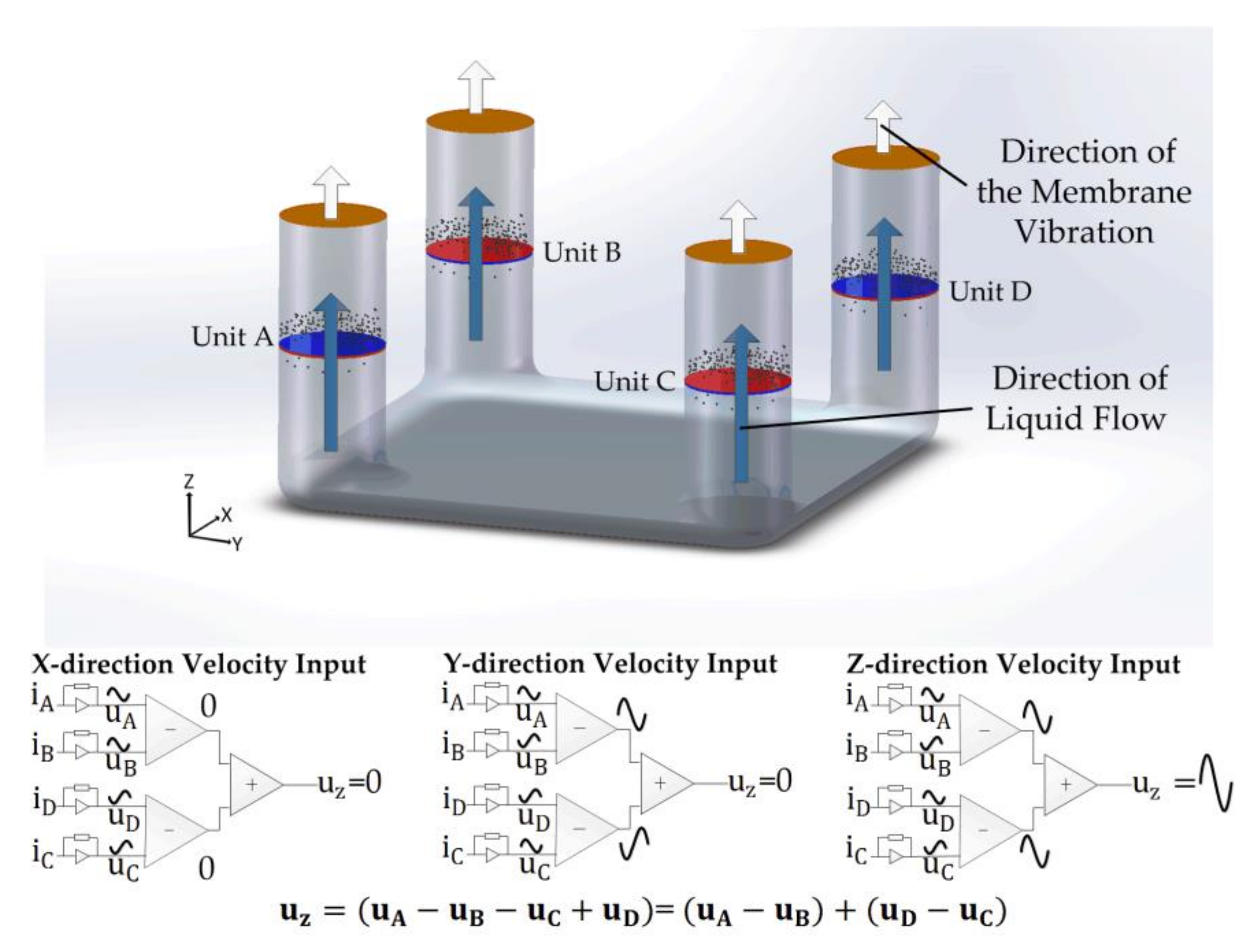
2. Structure and Operating Principle
3. Fabrication
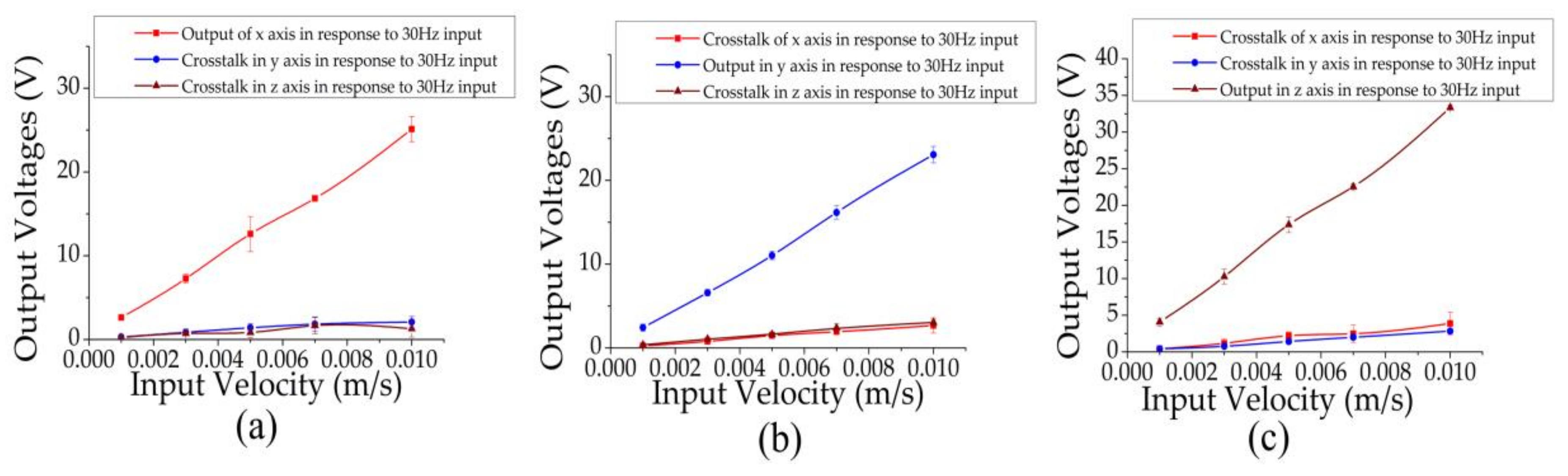
4. Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Deng, T.; Chen, D.Y.; Wang, J.B.; Chen, J.; He, W.T.; Fan, Y.J. A MEMS based electrochemical seismic sensor. In Proceedings of the 17th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS & EUROSENSORS XXVII), Barcelona, Spain, 16–20 June 2013; pp. 920–923. [Google Scholar]
- Huang, H.; Carande, B.; Tang, R.; Oiler, J.; Dmitriy, Z.; Vadim, A.; Yu, H. Development of a micro seismometer based on molecular electronic transducer technology for planetary exploration. In Proceedings of the 2013 IEEE 26th International Conference on Micro Electro Mechanical Systems (MEMS), Taipei, Taiwan, 22–24 January 2013; pp. 629–632. [Google Scholar]
- Abramovich, I.A.; Zhu, T. Next Generation Robust Low Noise Seismometer for Nuclear Monitoring. In Proceedings of the 30th Monitoring Research Review: Ground-Based Nuclear Explosion Monitoring Technologies, Portsmouth, VA, USA, 23–25 September 2008. [Google Scholar]
- Milligan, D.J.; Homeijer, B.; Walmsley, R. An ultra-low noise MEMS accelerometer for seismic imaging. In Proceedings of the IEEE Sensors, Limerick, Ireland, 28–31 October 2011; pp. 1281–1284. [Google Scholar]
- Hons, M.S.; Stewart, R.R.; Lawton, D.C.; Bertram, M.B.; Hauer, G. Field data comparisons of MEMS accelerometers and analog geophones. Lead. Edge 2008, 27, 896–903. [Google Scholar] [CrossRef]
- Sun, B.; Li, H.; Sun, X. A study based on real-time data acquisition system of intelligent seismometers in two dimension seismic prospecting. In Proceedings of the 2012 International Conference on Mechatronics and Automation (ICMA), Chengdu, China, 5–8 August 2012; pp. 2400–2404. [Google Scholar]
- Ubertini, F.; Cavalagli, N.; Kita, A.; Comanducci, G. Assessment of a monumental masonry bell-tower after 2016 central Italy seismic sequence by long-term SHM. Bull. Earthq. Eng. 2018, 16, 775–801. [Google Scholar] [CrossRef]
- Clementi, F.; Pierdicca, A.; Formisano, A.; Catinari, F.; Lenci, S. Numerical model upgrading of a historical masonry building damaged during the 2016 Italian earthquakes: The case study of the Podestà palace in Montelupone (Italy). J. Civ. Struct. Health Monit. 2017, 7, 703–717. [Google Scholar] [CrossRef]
- Deraemaeker, A.; Reynders, E.; De Roeck, G.; Kullaa, J. Vibration-based structural health monitoring using output-only measurements under changing environment. Mech. Syst. Signal Process. 2008, 22, 34–56. [Google Scholar] [CrossRef]
- Krstevska, L.; Tashkov, L.; Naumovski, N.; Florio, G.; Formisano, A.; Fornaro, A.; Landolfo, R. In-situ experimental testing of four historical buildings damaged during the 2009 L’Aquila earthquake. In Proceedings of the Final Conference on COST ACTION C26: Urban Habitat Constructions under Catastrophic Events, Naples, Italy, 16–18 September 2010; pp. 427–432, ISBN 978-041560685-1. [Google Scholar]
- Gentile, C.; Gallino, N. Ambient vibration testing and structural evaluation of an historic suspension footbridge. Adv. Eng. Softw. 2008, 39, 356–366. [Google Scholar] [CrossRef]
- Kavitha, S.; Daniel, R.J.; Sumangala, K. Design and Analysis of MEMS Comb Drive Capacitive Accelerometer for SHM and Seismic Applications. Measurement 2016, 93, 327–339. [Google Scholar] [CrossRef]
- Liu, H.; Pike, W.T. A micromachined angular-acceleration sensor for geophysical applications. Appl. Phys. Lett. 2016, 109, 173506. [Google Scholar] [CrossRef]
- Laudati, A.; Mennella, F.; Giordano, M.; D’Altrui, G.; Tassini, C.C.; Cusano, A. A fiber-optic Bragg grating seismic sensor. IEEE Photonics Technol. Lett. 2007, 19, 1991–1993. [Google Scholar] [CrossRef]
- Lindsey, N.J.; Martin, E.R.; Dreger, D.S.; Freifeld, B.; Cole, S.; James, S.R.; Ajo-Franklin, J.B. Fiber-Optic Network Observations of Earthquake Wavefields. Geophys. Res. Lett. 2017, 44, 11792–11799. [Google Scholar] [CrossRef]
- Edalatfar, F.; Yaghootkar, B.; Qureshi, A.Q.A.; Azimi, S.; Bahreyni, B. Design, fabrication and characterization of a high performance MEMS accelerometer. In Proceedings of the Sensors, Orlando, FL, USA, 30 October–3 November 2016; pp. 1–3. [Google Scholar]
- Laine, J.; Mougenot, D. Benefits of MEMS based seismic accelerometers for oil exploration. In Proceedings of the Solid-State Sensors, Actuators and Microsystems Conference, Lyon, France, 10–14 June 2007; pp. 1473–1477. [Google Scholar]
- Deng, T.; Chen, D.; Wang, J.; Chen, J.; He, W. A MEMS based electrochemical vibration sensor for seismic motion monitoring. J. Microelectromech. Syst. 2014, 23, 92–99. [Google Scholar] [CrossRef]
- Antonov, A.; Shabalina, A.; Razin, A.; Avdyukhina, S.; Egorov, I.; Agafonov, V. Low-Frequency Seismic Node Based on Molecular-Electronic Transfer Sensors for Marine and Transition Zone Exploration. J. Atmos. Ocean. Technol. 2017, 34, 1743–1748. [Google Scholar] [CrossRef]
- Chen, D.Y.; Hsiao, N.C.; Wu, Y.M. The Earthworm based earthquake alarm reporting system in Taiwan. Bull. Seismol. Soc. Am. 2015, 105, 568–579. [Google Scholar] [CrossRef]
- Havskov, J.; Alguacil, G. Instrumentation in Earthquake Seismology; Springer: Berlin/Heidelberg, Germany, 2004; pp. 1–5. [Google Scholar]
- Hughes, C.N.; Dutta, D.; Bashirzadeh, Y.; Ahmed, K.; Qian, S. Measuring Shear Stress with A MicroFluidic Sensor to Improve Aerodynamic Efficiency. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; p. 1919. [Google Scholar]
- Huang, H.; Carande, B.; Tang, R.; Oiler, J. A Micro Seismometer Based on Molecular Electronic Transducer Technology for Planetary Exploration. Appl. Phys. Lett. 2013, 102, 4524–4546. [Google Scholar] [CrossRef]
- Sun, Z.; Agafonov, V.; Egorov, E. The influence of the boundary condition on anodes for solution of convection–diffusion equation with the application to a four-electrode electrochemical cell. J. Electroanal. Chem. 2011, 661, 157–161. [Google Scholar] [CrossRef]
- B&K Vibration Exciter: Type 4808. Available online: https://www.bksv.com/en/products/shakers-and-exciters/measurement-exciters/permanent-magnet-vibration-exciter-type-4808 (accessed on 15 October 2015).






© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Sun, Z.; Li, G.; Chen, D.; Wang, J.; Chen, J. A Monolithic Electrochemical Micro Seismic Sensor Capable of Monitoring Three-Dimensional Vibrations. Sensors 2018, 18, 1047. https://doi.org/10.3390/s18041047
Chen L, Sun Z, Li G, Chen D, Wang J, Chen J. A Monolithic Electrochemical Micro Seismic Sensor Capable of Monitoring Three-Dimensional Vibrations. Sensors. 2018; 18(4):1047. https://doi.org/10.3390/s18041047
Chicago/Turabian StyleChen, Lianhong, Zhenyuan Sun, Guanglei Li, Deyong Chen, Junbo Wang, and Jian Chen. 2018. "A Monolithic Electrochemical Micro Seismic Sensor Capable of Monitoring Three-Dimensional Vibrations" Sensors 18, no. 4: 1047. https://doi.org/10.3390/s18041047
APA StyleChen, L., Sun, Z., Li, G., Chen, D., Wang, J., & Chen, J. (2018). A Monolithic Electrochemical Micro Seismic Sensor Capable of Monitoring Three-Dimensional Vibrations. Sensors, 18(4), 1047. https://doi.org/10.3390/s18041047






