An Improved Positioning Method for Two Base Stations in AIS
Abstract
:1. Introduction
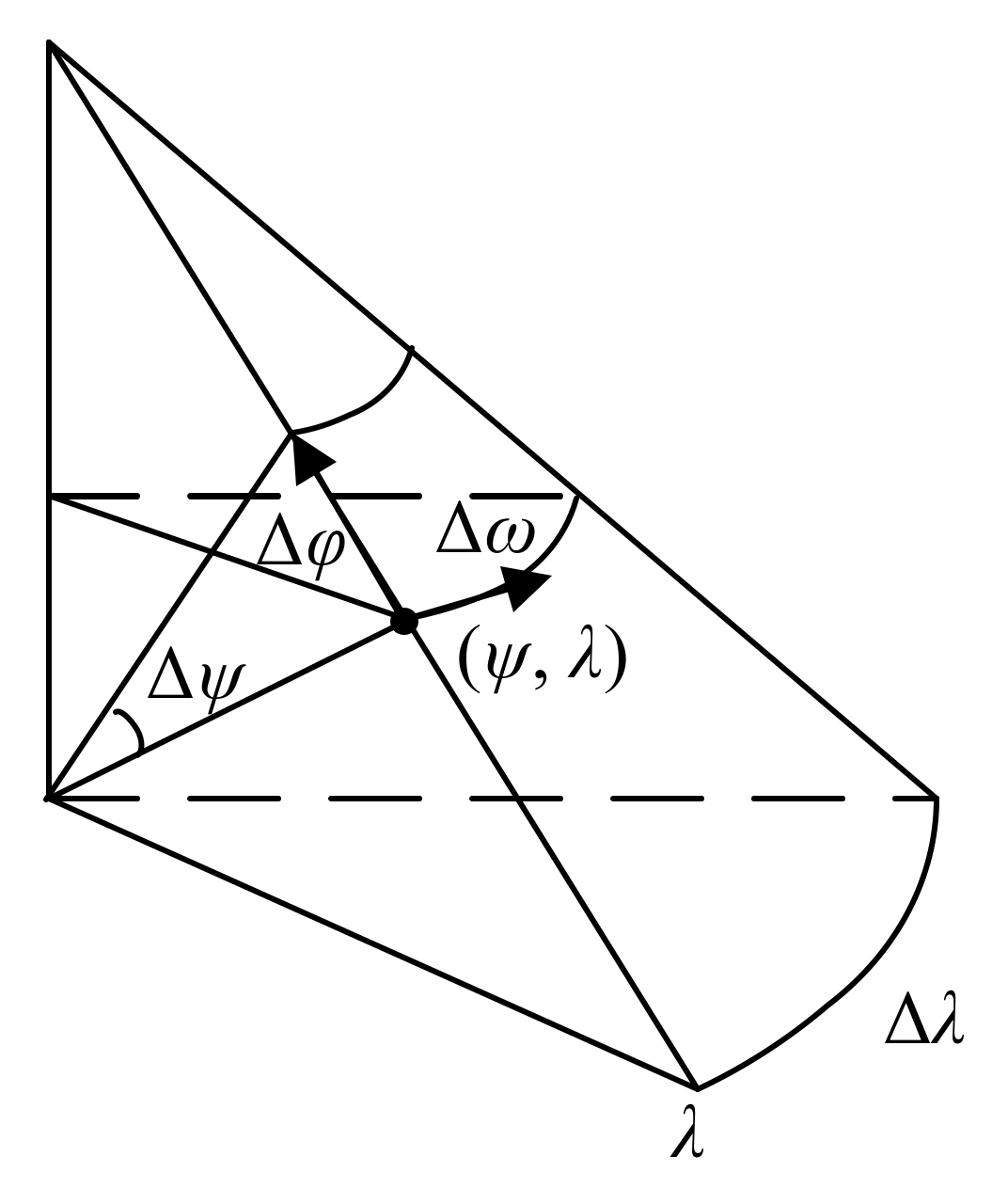
2. Displacement Correction Position Estimation Method
3. Improved Displacement Correction Position Estimation Method
3.1. Improved Method for Accelerated Motion
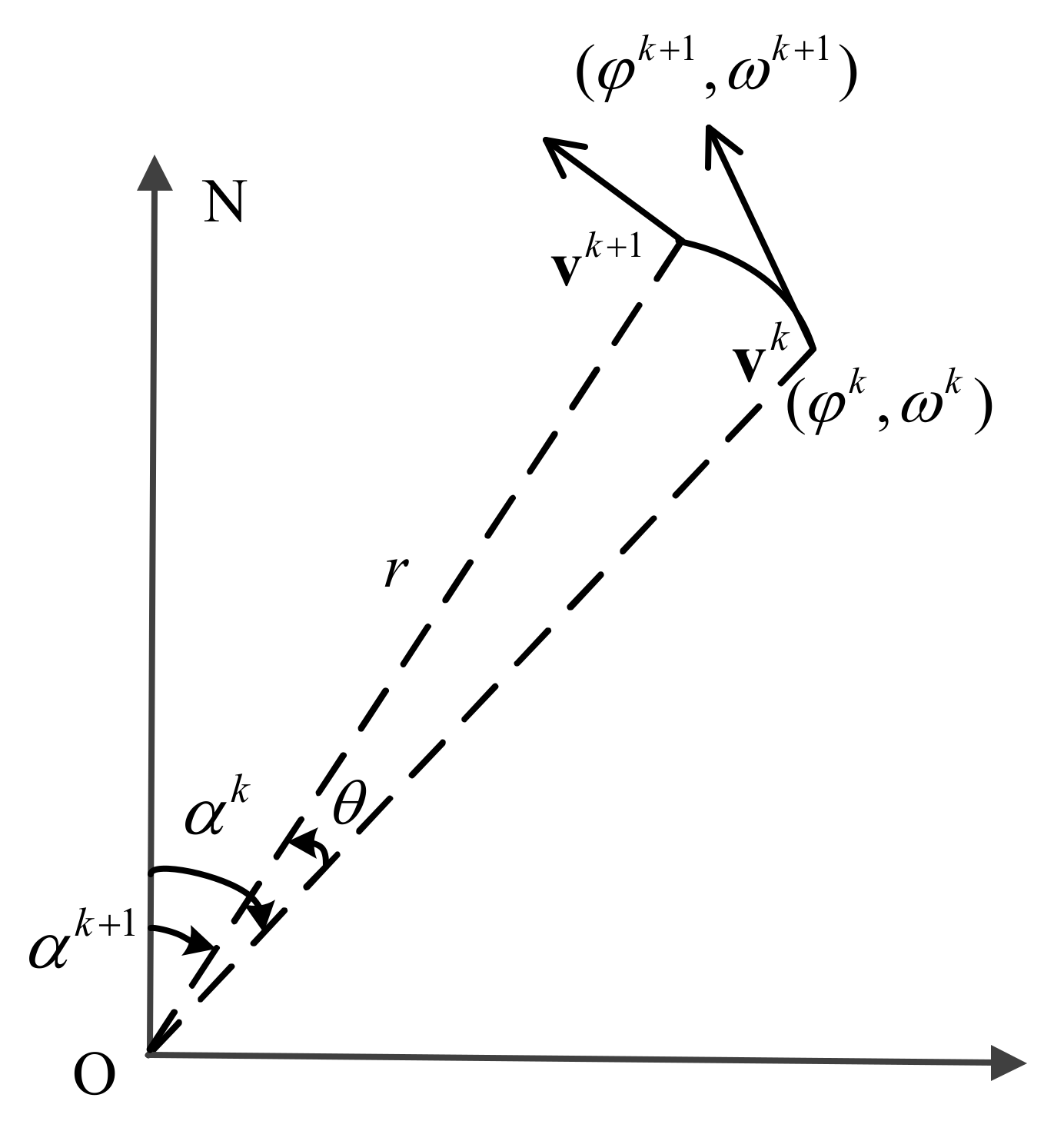
3.2. Improved Method for Turning Motion
3.3. Motion Model Adaptation Selection
4. Simulation Results and Analysis
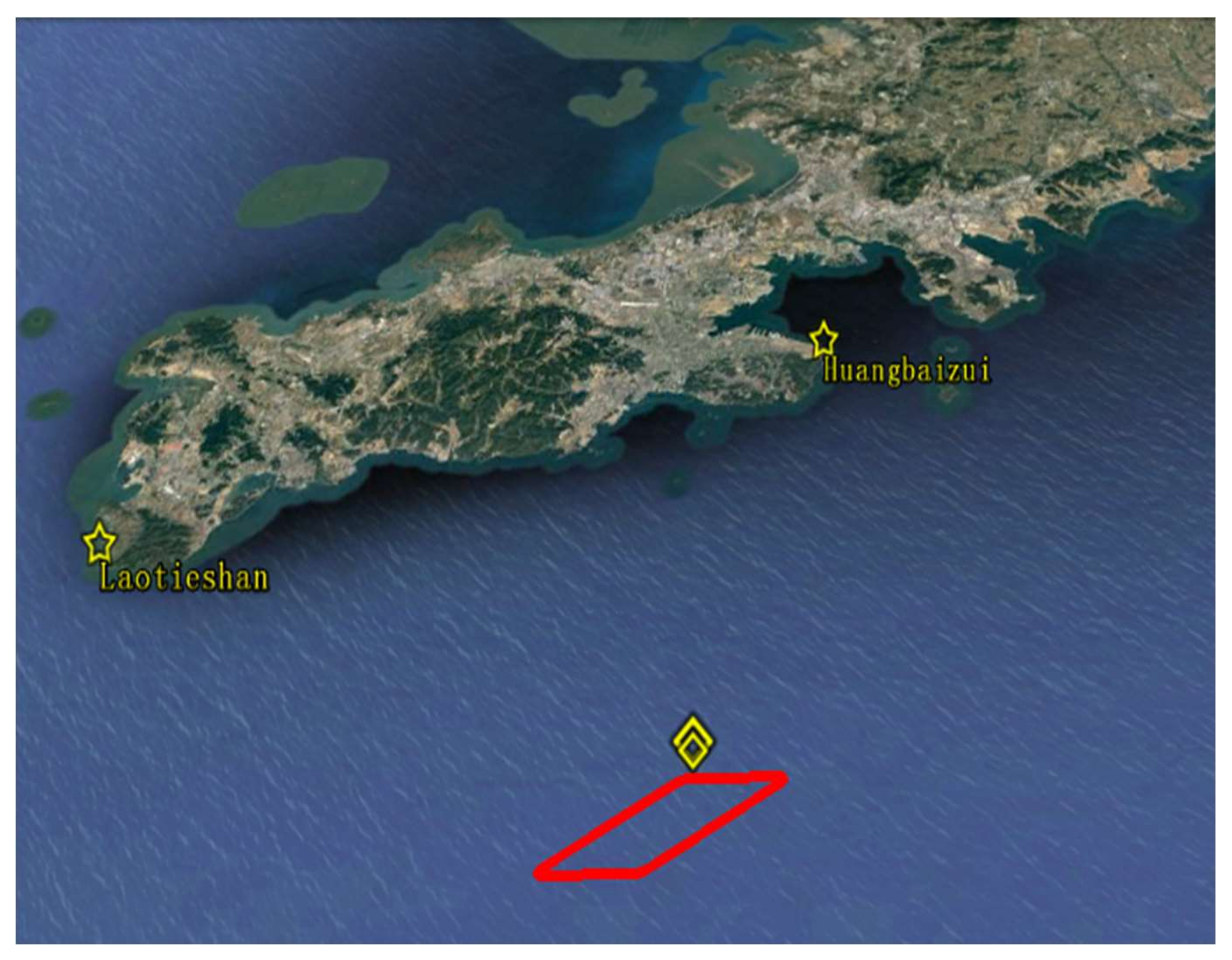
4.1. Simulation Scenario
4.2. Comparison and Analysis
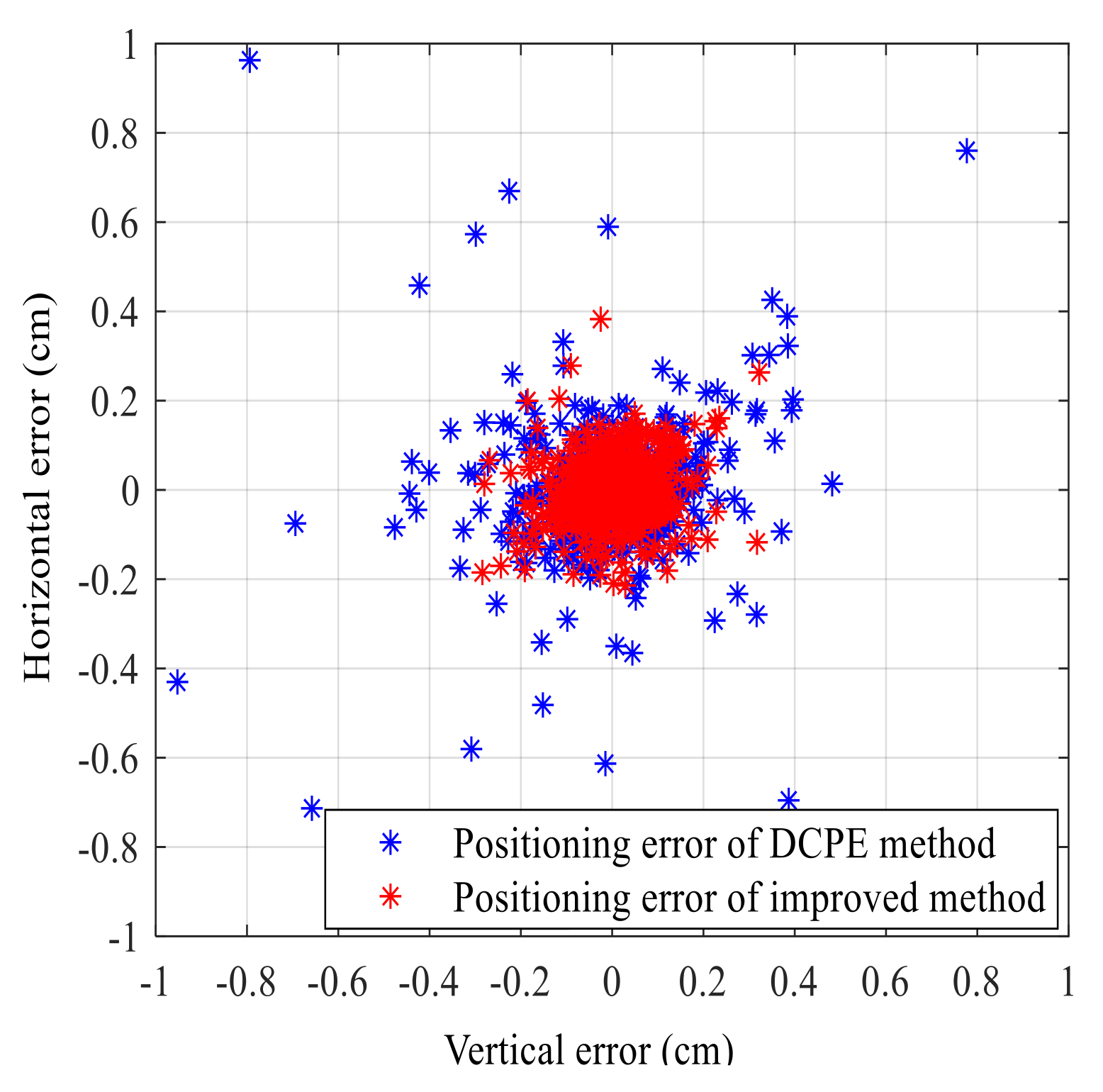
4.2.1. Horizontal and Vertical Errors
4.2.2. Position Errors
4.2.3. Errors Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Del Peral-Rosado, J.A.; Castillo, R.E.I.; Mıguez-Sánchez, J.; Navarro-Gallardo, M.; Garcıa-Molina, J.A.; López-Salcedo, J.A.; Seco-Granados, G.; Zanier, F.; Crisci, M. Performance analysis of hybrid GNSS and LTE Localization in urban scenarios. In Proceedings of the 8th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing (NAVITEC), Noordwijk, The Netherlands, 14–16 December 2016; pp. 1–8. [Google Scholar]
- Bayat, M.; Madani, M.H. Loran phase code revisited for continuous wave interference cancellation. IET Sci. Meas. Technol. 2017, 11, 322–330. [Google Scholar] [CrossRef]
- Song, S.P.; Choi, H.H.; Kim, Y.B.; Lee, S.J.; Park, C. Verification of GPS aided error compensation method for eLoran using raw TOA measurements. In Proceedings of the 11th International Conference on Control, Automation and Systems, Gyeonggi-do, Korea, 26–29 October 2011; pp. 1620–1624. [Google Scholar]
- Johnson, G.; Shalaev, R.; Hartnett, R.; Swaszek, P.; Narins, M. Can LORAN meet GPS backup requirements? IEEE Aerosp. Electron. Syst. Mag. 2005, 20, 3–12. [Google Scholar] [CrossRef]
- Helfrick, A. Question: Alternate position, navigation timing, APNT? Answer: ELORAN. In Proceedings of the IEEE/AIAA 33rd Digital Avionics Systems Conference (DASC), Colorado Springs, CO, USA, 5–9 October 2014; pp. 3C3-1–3C3-9. [Google Scholar]
- Wang, L.; Li, K.; Zhang, J.; Ding, Z. Soft Fault Diagnosis and Recovery Method Based on Model Identification in Rotation FOG Inertial Navigation System. IEEE Sens. J. 2017, 17, 5705–5716. [Google Scholar] [CrossRef]
- Du, H.; Sun, Q.; Zhang, Y.; Qi, Z.; Wen, Y. Inertial navigation system positioning assisted by star sensor. In Proceedings of the International Conference on Control, Automation and Information Sciences (ICCAIS), Ansan, Korea, 27–29 October 2016; pp. 183–187. [Google Scholar]
- Sineglazov, V. Main features of terrain-aided navigation systems. In Proceedings of the IEEE 3rd International Conference on Methods and Systems of Navigation and Motion Control (MSNMC), Kiev, Ukraine, 14–17 October 2014; pp. 49–52. [Google Scholar]
- Mistary, P.V.; Chile, R.H. Real time Vehicle tracking system based on ARM7 GPS and GSM technology. In Proceedings of the Annual IEEE India Conference (INDICON), New Delhi, India, 17–20 December 2015; pp. 1–6. [Google Scholar]
- Essaadali, R.; Jebali, C.; Grati, K.; Kouki, A. AIS data exchange protocol study and embedded software development for maritime navigation. In Proceedings of the IEEE 28th Canadian Conference on Electrical and Computer Engineering (CCECE), Halifax, NS, Canada, 3–6 May 2015; pp. 1594–1599. [Google Scholar]
- Johnson, G.; Swaszek, P. Feasibility Study of R-Mode Combining MF DGNSS, AIS, and eLoran Transmissions. 2014. Available online: http://www.accseas.eu/publications/r-mode-feasibility-study/ (accessed on 21 February 2018).
- Johnson, G.; Swaszek, P.; Alberding, J.; Hoppe, M.; Oltmann, J.H. The Feasibility of R-Mode to Meet Resilient PNT Requirements for E-Navigation. In Proceedings of the 27th International Technical Meeting of the Satellite Division of the Institute of Navigation, Tampa, FL, USA, 8–12 September 2014; pp. 3076–3100. [Google Scholar]
- Julia, H.; Stefan, G. Launch of R-Mode Baltic Project—An Alternative Navigation System at Sea. 2017. Available online: http://www.dlr.de/dlr/en/desktopdefault.aspx/tabid-10260/370_read-24695#/gallery/28882 (accessed on 21 February 2018).
- Zhang, S.F.; Hu, Q. Ship Autonomous Positioning System Based on Automatic Identification System (AIS). CN Patent 102305936B, 17 July 2013. [Google Scholar]
- Zhang, J.B.; Zhang, S.F.; Wang, J.P. Pseudorange Measurement Method Based on AIS Signals. Sensors 2017, 17, 1183. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.Y.; Zhang, S.F.; Sun, X.W. The Additional Secondary Phase Correction System for AIS Signals. Sensors 2017, 17, 736. [Google Scholar] [CrossRef] [PubMed]
- Hu, Q.; Jiang, Y.; Zhang, J.B.; Sun, X.W.; Zhang, S.F. Development of an Automatic Identification System Autonomous Positioning System. Sensors 2015, 15, 28574–28591. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Zhang, S.F.; Yang, D.K. A novel position estimation method based on displacement correction in AIS. Sensors 2014, 14, 17376–17389. [Google Scholar] [CrossRef] [PubMed]
- Batista, P.; Silvestre, C.; Oliveira, P. Pseudo-range navigation with clock offset and propagation speed estimation. In Proceedings of the 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 7636–7641. [Google Scholar]
- Feng, K.L.; Li, A.; Qin, F.J. Integrated navigation method based on pseudo-range/pseudo-range rate/dual-differenced carrier phase. In Proceedings of the Chinese Automation Congress (CAC), Wuhan, China, 27–29 November 2015; pp. 1778–1782. [Google Scholar]
- Tanaka, Y.; Okuno, J.; Okubo, S. A new method for the computation of global viscoelastic post-seismic deformation in a realistic earth model (I)—Vertical displacement and gravity variation. Geophys. J. Int. 2006, 164, 273–289. [Google Scholar] [CrossRef]
- Tanaka, Y.; Okuno, J.; Okubo, S. A new method for the computation of global viscoelastic post-seismic deformation in a realistic earth model (II)-horizontal displacement. Geophys. J. Int. 2007, 170, 1031–1052. [Google Scholar] [CrossRef]
- Gao, L.P.; Sun, H.; Liu, M.N.; Jiang, Y. TDOA collaborative localization algorithm based on PSO and Newton iteration in WGS-84 coordinate system. In Proceedings of the IEEE 13th International Conference on Signal Processing (ICSP), Chengdu, China, 6–10 November 2016; pp. 1571–1575. [Google Scholar]
- Kutil, R.; Flatz, M.; Vajtersic, M. Improvements in Approximation Performance and Parallelization of Nonnegative Matrix Factorization with Newton Iteration. In Proceedings of the International Conference on High Performance Computing & Simulation (HPCS), Genoa, Italy, 17–21 July 2017; pp. 887–888. [Google Scholar]
- Tordal, S.S.; Løvsland, P.O.; Hovland, G. Testing of wireless sensor performance in Vessel-to-Vessel Motion Compensation. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 654–659. [Google Scholar]
- Xu, B.; Bai, J.; Wang, G.; Zhang, Z.; Huang, W. Cooperative navigation and localization for unmanned surface vessel with low-cost sensors. In Proceedings of the DGON Inertial Sensors and Systems (ISS), Karlsruhe, Germany, 16–17 September 2014; pp. 1–14. [Google Scholar]
- Fillmore, J.P. A Note on Rotation Matrices. IEEE Comput. Graph. App. 1984, 4, 30–33. [Google Scholar] [CrossRef]
- Jang, J.T.; Gong, H.C.; Lyou, J. Computed Torque Control of an aerospace craft using nonlinear inverse model and rotation matrix. In Proceedings of the 15th International Conference on Control, Automation and Systems (ICCAS), Busan, Korea, 13–16 October 2015; pp. 1743–1746. [Google Scholar]
- Ahmad, F.; Khan, R.A. Eigenvectors of a rotation matrix. Q. J. Mech. Appl. Math. 2009, 62, 297–310. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Y. Direction and polarization estimation using quaternion and polarization rotation matrix. In Proceedings of the IEEE Symposium on Electrical & Electronics Engineering (EEESYM), Kuala Lumpur, Malaysia, 24–27 June 2012; pp. 319–322. [Google Scholar]
- Wang, S.; Gao, S.; Yang, W. Ship route extraction and clustering analysis based on automatic identification system data. In Proceedings of the Eighth International Conference on Intelligent Control and Information Processing (ICICIP), Hangzhou, China, 3–5 November 2017; pp. 33–38. [Google Scholar]
- Ren, W.; Li, G.; Lv, J. Analysis of Adopting Mobile Position System Based on GPSOne Technique in VTS System. In Proceedings of the International Conference on Intelligent System Design and Engineering Application, Changsha, China, 13–14 October 2010; pp. 281–284. [Google Scholar]
- Liu, C.Q. Vibratory source’s search and localization algorithm of Newton iteration based on method of weighted least squares. In Proceedings of the International Conference on Measurement, Information and Control, Harbin, China, 18–20 May 2012; pp. 988–991. [Google Scholar]
- Wei, Y. A revision of the Newton iteration format for nonlinear equation. In Proceedings of the Fourth International Workshop on Advanced Computational Intelligence, Wuhan, China, 19–21 October 2011; pp. 540–541. [Google Scholar]




| Name | MMSI | Latitude | Longitude |
|---|---|---|---|
| Laotieshan | 4,131,101 | N | E |
| Huangbaizui | 4,131,104 | N | E |
| Method | Error | 1~500 s | 501~550 s | 551~1050 s | 1051~1100 s | 1101~1600 s | 1601~1650 s | 1651~2150 s | 2151~2200 s |
|---|---|---|---|---|---|---|---|---|---|
| DCPE Method | η1 | 0.3826 | 0.9627 | 0.1457 | 0.2402 | 0.2710 | 0.7601 | 0.1382 | 0.1689 |
| η2 | 0.3934 | 0.3165 | 0.1948 | 0.1868 | 0.2575 | 1.0614 | 0.2291 | 0.1959 | |
| μ1 | −0.0010 | 0.0276 | −0.0007 | 0.0120 | 0.0009 | 0.0249 | −0.0010 | −0.0262 | |
| μ2 | 0.0014 | −0.0724 | 0.0019 | −0.0195 | −0.0025 | 0.0524 | 0.0003 | −0.0175 | |
| σ1 | 0.0444 | 0.2673 | 0.0251 | 0.1024 | 0.0459 | 0.2624 | 0.0271 | 0.0674 | |
| σ2 | 0.0445 | 0.2358 | 0.0329 | 0.1107 | 0.0534 | 0.3429 | 0.0353 | 0.0808 | |
| Improved Method | η1 | 0.2180 | 0.2043 | 0.1048 | 0.1996 | 0.1462 | 0.2633 | 0.1057 | 0.0766 |
| η2 | 0.3174 | 0.1674 | 0.1805 | 0.1200 | 0.2280 | 0.3222 | 0.1816 | 0.0780 | |
| μ1 | −0.00001 | −0.0019 | 0.0001 | 0.0023 | −0.0008 | 0.0128 | −0.0003 | −0.0035 | |
| μ2 | 0.0004 | 0.0177 | 0.0016 | 0.0018 | −0.0006 | 0.0229 | −0.0007 | 0.0001 | |
| σ1 | 0.0426 | 0.0800 | 0.0244 | 0.0494 | 0.0420 | 0.0952 | 0.0259 | 0.0390 | |
| σ2 | 0.0442 | 0.0834 | 0.0302 | 0.0612 | 0.0466 | 0.1236 | 0.0347 | 0.0415 |
| No. | Horizontal Error | Vertical Error | ||
|---|---|---|---|---|
| 1 | 5.009371978 | 6.116692350 | 0.136755441 | −0.033688209 |
| 2 | 5.009364103 | 6.116582698 | −0.044890233 | 0.178701572 |
| 3 | 5.009360177 | 6.116480498 | 0.133527424 | −0.354018592 |
| 4 | 5.009360530 | 6.116386250 | −0.613144241 | −0.014801477 |
| 5 | 5.009364834 | 6.116299943 | 0.038769839 | −0.400999096 |
| 6 | 5.009373314 | 6.116221335 | −0.481755011 | −0.151736104 |
| 7 | 5.009385773 | 6.116150846 | −0.083722842 | −0.476183031 |
| 8 | 5.009402483 | 6.116088651 | −0.233052817 | 0.274446059 |
| 9 | 5.009422998 | 6.116034472 | 0.458114784 | −0.422002996 |
| 10 | 5.009447685 | 6.115988481 | 0.589510173 | −0.008883503 |
| 11 | 5.009476324 | 6.115950728 | 0.115658450 | −0.192622662 |
| 12 | 5.009508806 | 6.115921259 | 0.962727494 | −0.793874836 |
| 13 | 5.009545403 | 6.115900175 | −0.075081556 | −0.693991153 |
| 14 | 5.009585874 | 6.115887465 | −0.175334603 | −0.333361476 |
| 15 | 5.009630160 | 6.115883378 | 0.669634066 | −0.225495902 |
| 16 | 5.009678183 | 6.115887176 | 0.202885538 | −0.298708880 |
| 17 | 5.009730051 | 6.115899711 | 0.259243149 | −0.218549897 |
| No. | Horizontal Error | Vertical Error | ||
|---|---|---|---|---|
| 1 | 5.009371995 | 6.116692369 | 0.052833868 | 0.038729669 |
| 2 | 5.009364061 | 6.116582636 | 0.072796110 | −0.032886895 |
| 3 | 5.009360236 | 6.116480577 | 0.059390886 | −0.007025953 |
| 4 | 5.009360511 | 6.116386303 | 0.036391146 | 0.029988286 |
| 5 | 5.009364878 | 6.116299822 | −0.137737964 | 0.088876636 |
| 6 | 5.009373319 | 6.116221349 | 0.006360655 | 0.085991809 |
| 7 | 5.009385838 | 6.116150860 | 0.015130796 | 0.111074183 |
| 8 | 5.009402406 | 6.116088433 | −0.190604914 | −0.026010386 |
| 9 | 5.009423040 | 6.116034233 | −0.068020249 | 0.087595125 |
| 10 | 5.009447679 | 6.115988256 | −0.033166051 | 0.009970006 |
| 11 | 5.009476329 | 6.115950615 | 0.097515659 | 0.020200008 |
| 12 | 5.009508939 | 6.115921190 | 0.003789785 | 0.041866405 |
| 13 | 5.009545475 | 6.115900117 | 0.017615842 | 0.063760294 |
| 14 | 5.009585895 | 6.115887434 | 0.056106653 | 0.006849625 |
| 15 | 5.009630184 | 6.115883145 | 0.102804730 | 0.105033462 |
| 16 | 5.009678249 | 6.115887169 | 0.038196622 | 0.049230991 |
| 17 | 5.009730064 | 6.115899593 | 0.051263916 | −0.011125038 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Wu, J.; Zhang, S. An Improved Positioning Method for Two Base Stations in AIS. Sensors 2018, 18, 991. https://doi.org/10.3390/s18040991
Jiang Y, Wu J, Zhang S. An Improved Positioning Method for Two Base Stations in AIS. Sensors. 2018; 18(4):991. https://doi.org/10.3390/s18040991
Chicago/Turabian StyleJiang, Yi, Jiani Wu, and Shufang Zhang. 2018. "An Improved Positioning Method for Two Base Stations in AIS" Sensors 18, no. 4: 991. https://doi.org/10.3390/s18040991
APA StyleJiang, Y., Wu, J., & Zhang, S. (2018). An Improved Positioning Method for Two Base Stations in AIS. Sensors, 18(4), 991. https://doi.org/10.3390/s18040991





