Multi-Frequency Signal Detection Based on Frequency Exchange and Re-Scaling Stochastic Resonance and Its Application to Weak Fault Diagnosis
Abstract
:1. Introduction
2. Basic Theory
2.1. Classical Stochastic Resonance (CSR)
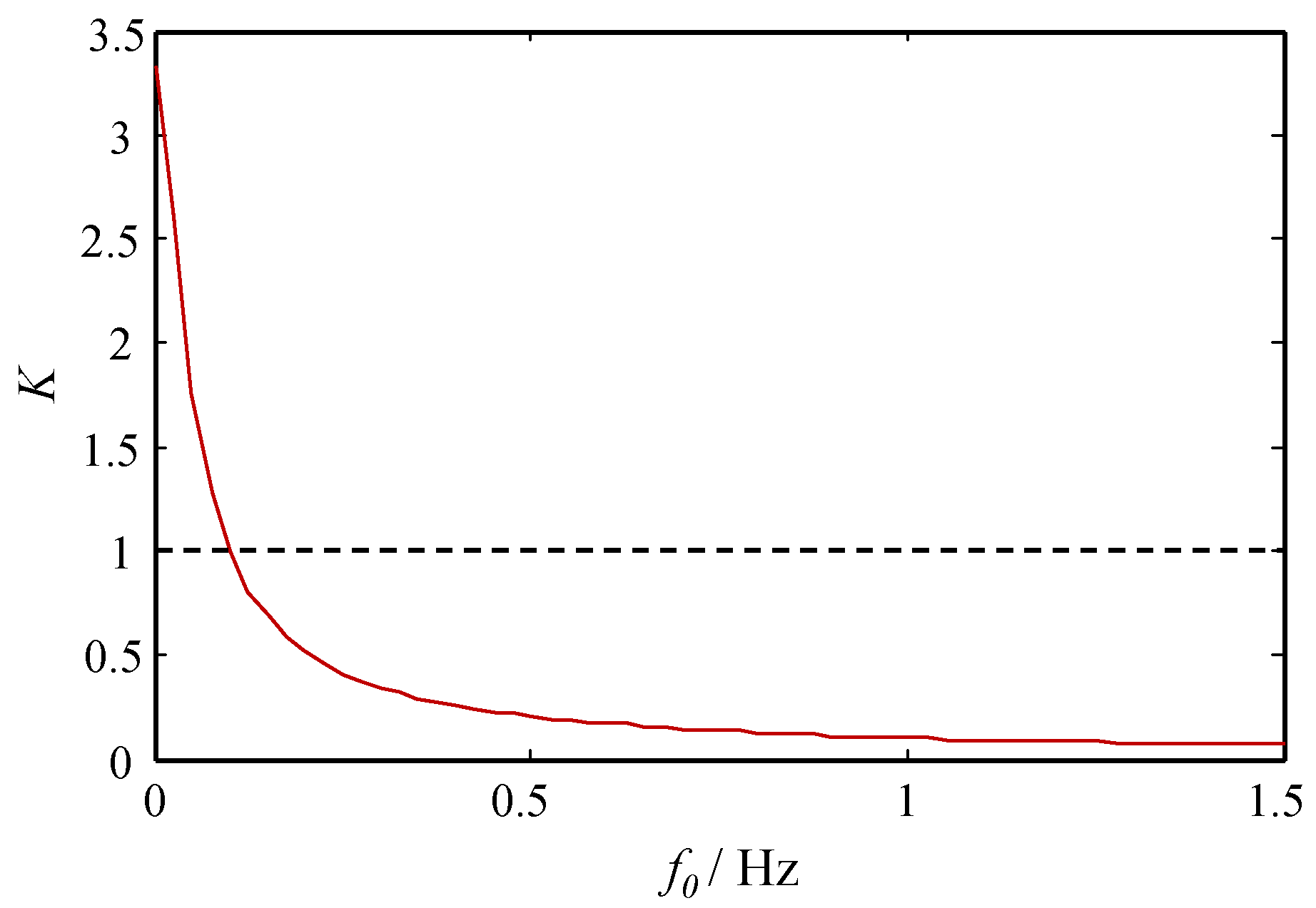
2.2. Frequency Re-Scaling Stochastic Resonance
3. Frequency Exchange and Re-Scaling Stochastic Resonance (FERSR)
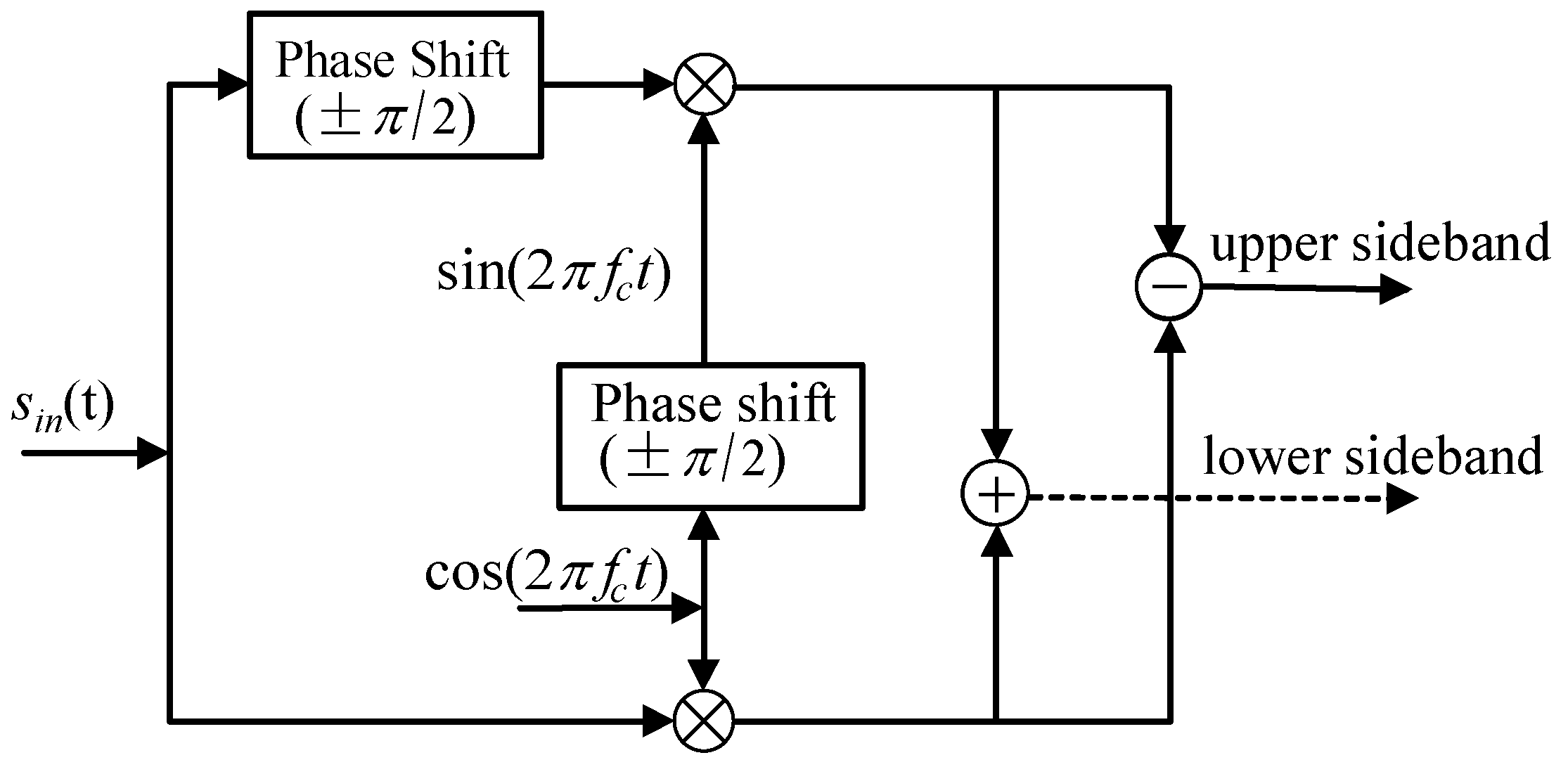
3.1. The Principle of Frequency Exchange Based on SSB Modulation
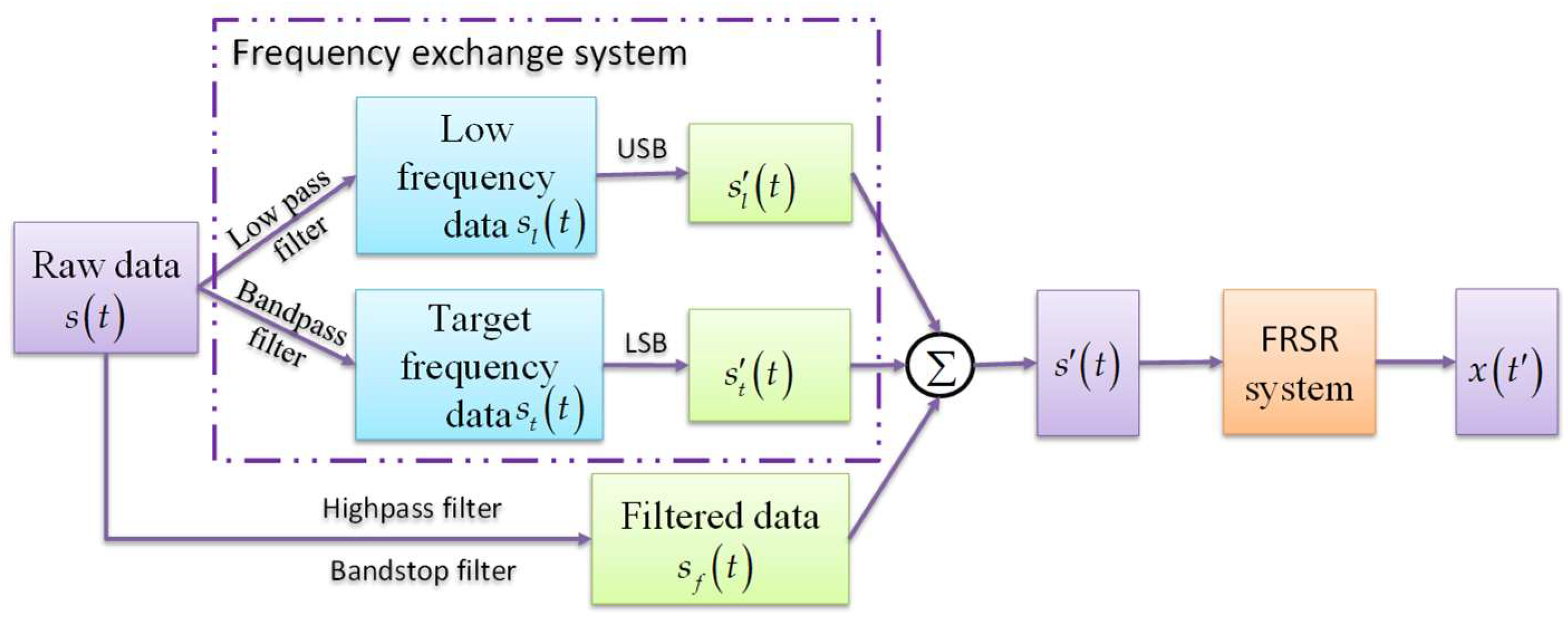
3.2. Signal Processing Model Based on FERSR
4. Multi-Frequency Signal Detection Based on FERSR
5. Numerical Simulation and Experimental Verification
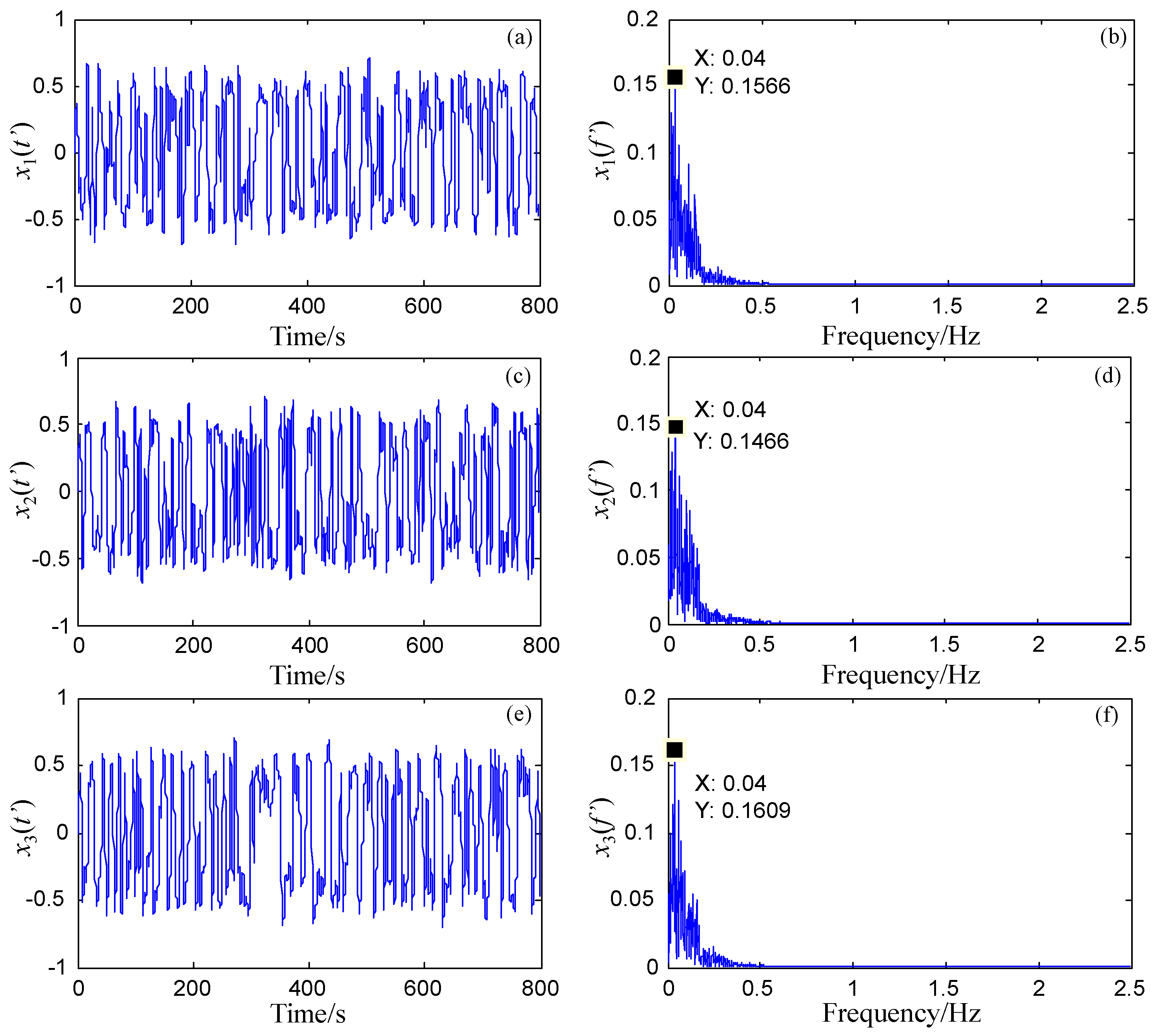
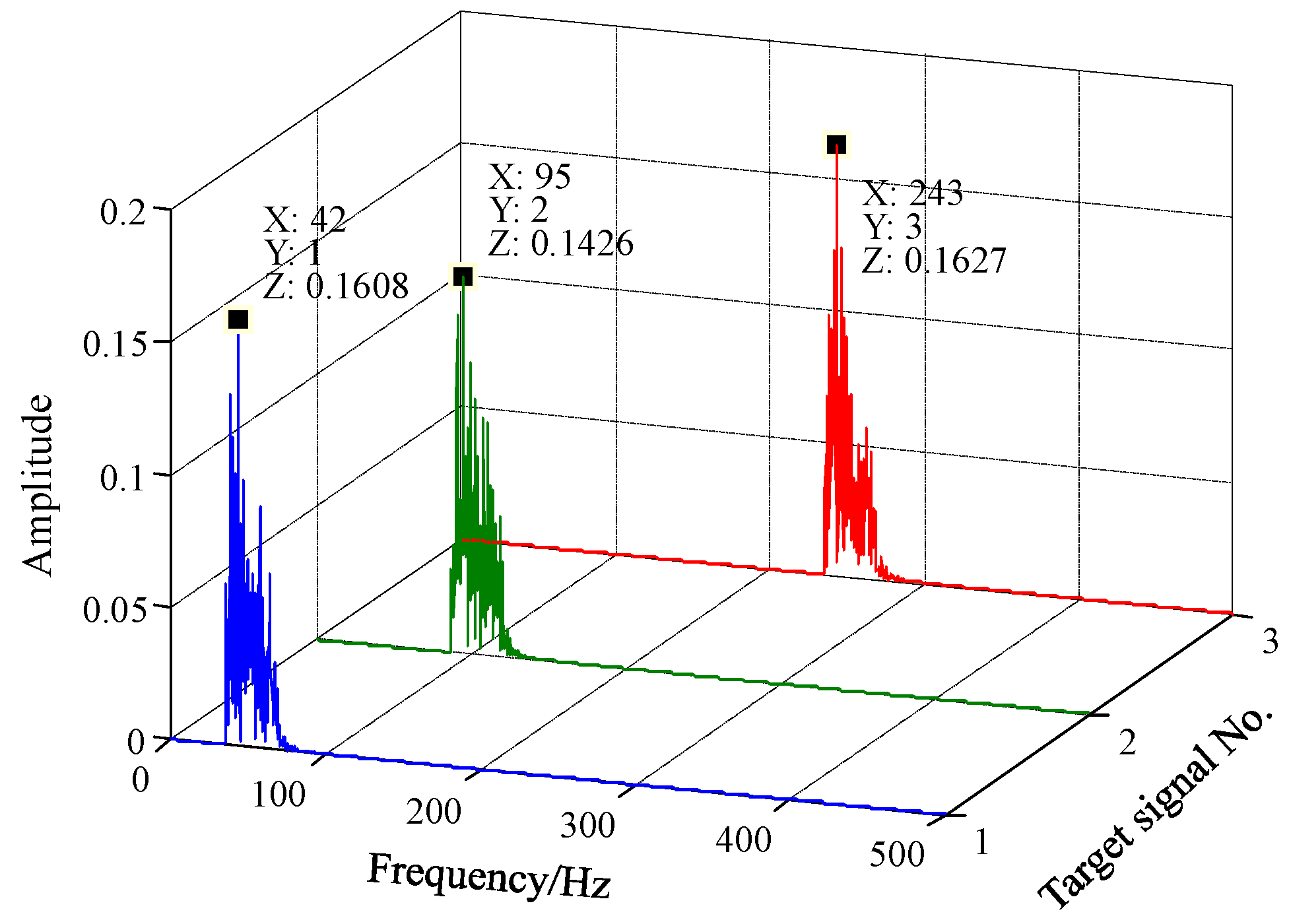
5.1. Numerical Simulation
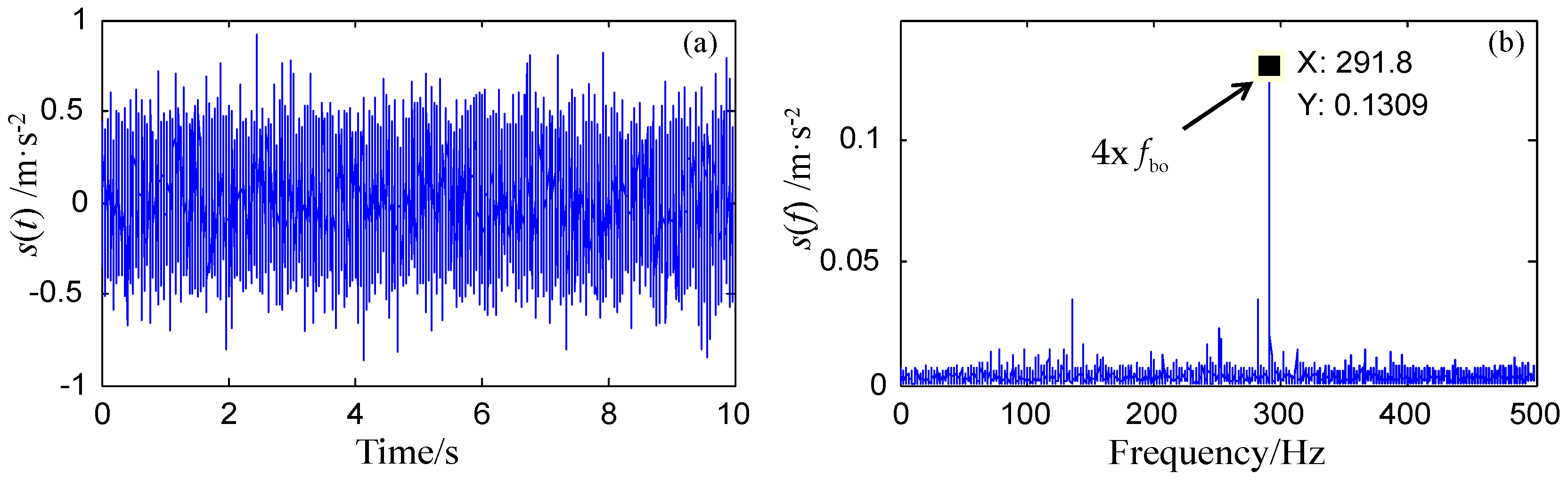
5.2. Case 1: Application to Fault Diagnosis of Rolling Bearing Outer Ring
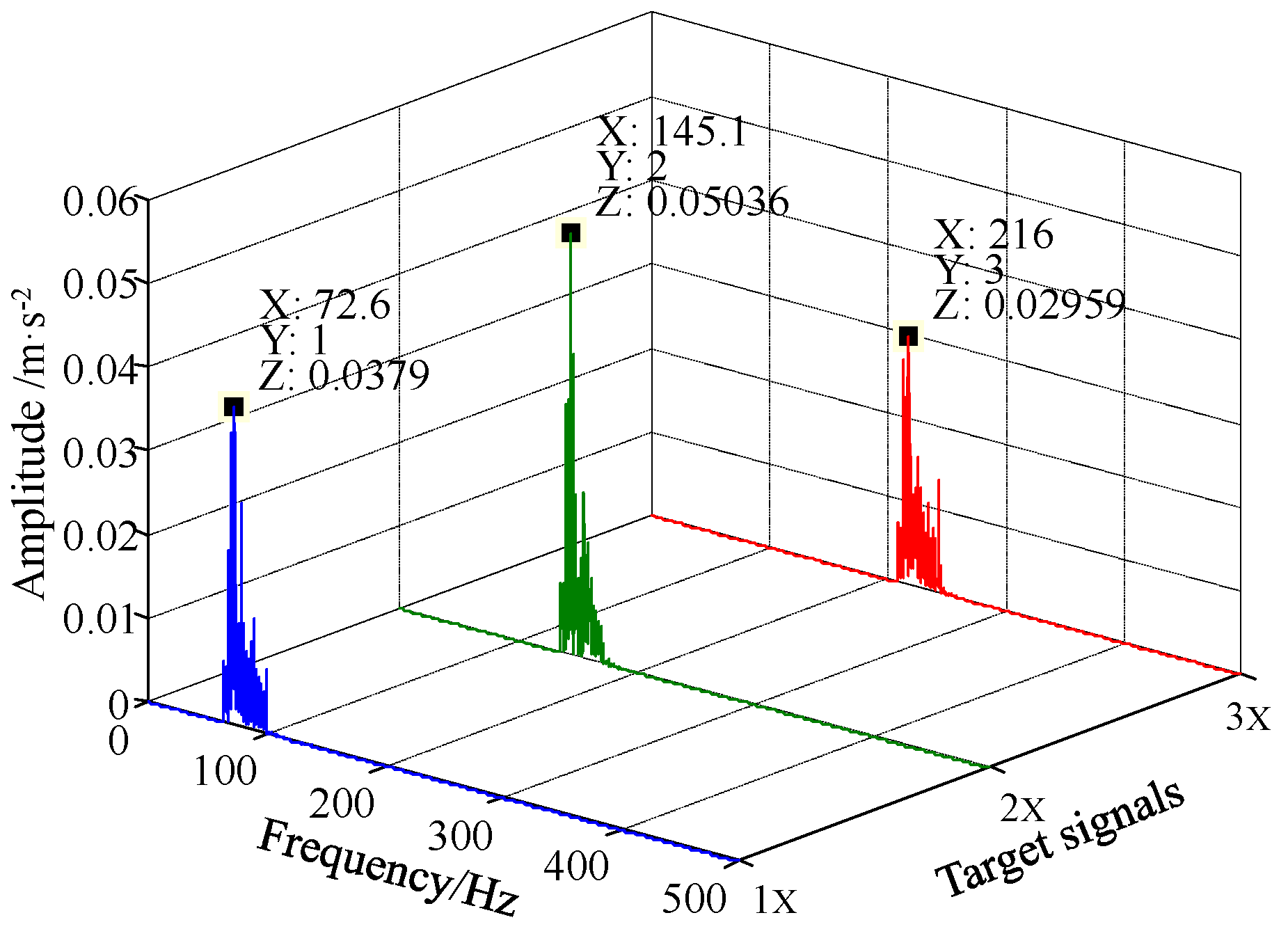
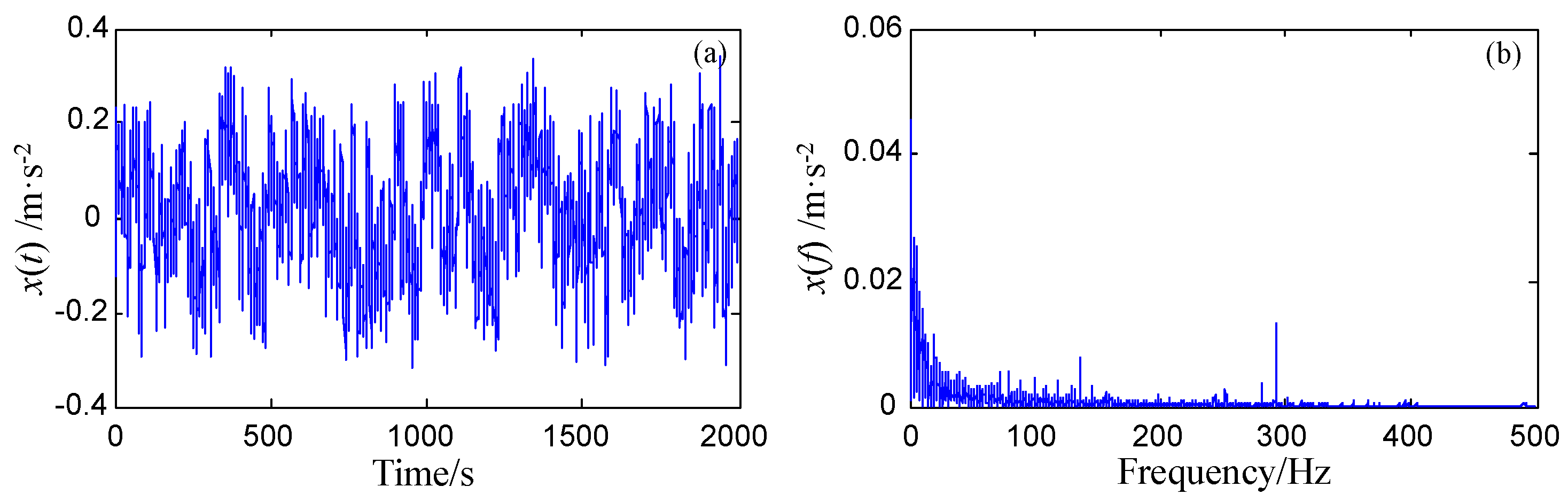
5.3. Case 2: Application to Diagnosis of Rotor Shaft-Bending Fault
5.4. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Jardine, A.K.S.; Lin, D.M.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Lee, J.; Wu, F.J.; Zhao, W.Y.; Ghaffari, M.; Liao, L.X.; Siegel, D. Prognostics and health management design for rotary machinery systems—Reviews, methodology and applications. Mech. Syst. Signal Process. 2014, 42, 314–334. [Google Scholar] [CrossRef]
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics. J. Sound Vib. 2006, 289, 1066–1090. [Google Scholar] [CrossRef]
- Yan, R.Q.; Gao, R.X.; Chen, X.F. Wavelets for fault diagnosis of rotary machines: A review with applications. Signal Process. 2014, 96, 1–15. [Google Scholar] [CrossRef]
- Lv, Y.; Yuan, R.; Song, G.B. Multivariate empirical mode decomposition and its application to fault diagnosis of rolling bearing. Mech. Syst. Signal Process. 2016, 81, 219–234. [Google Scholar] [CrossRef]
- Lai, Z.H.; Leng, Y.G. Generalized parameter-adjusted stochastic resonance of duffing oscillator and its application to weak-signal detection. Sensors 2015, 15, 21327–21349. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.G.; Ma, H.L.; Fu, S.; Zhang, J.Y. Theory and application of weak signal non-linear detection method for incipient fault diagnosis of mechanical equipments. J. Vib. Eng. 2011, 24, 529–538. [Google Scholar] [CrossRef]
- Benzi, R.; Sutera, A.; Vulpiani, A. The mechanism of stochastic resonance. J. Phys. A Math. Gen. 1981, 14, 453–457. [Google Scholar] [CrossRef]
- Fauve, S.; Heslo, F. Stochastic resonance in a bistable system. Phys. Lett. A 1983, 97, 5–7. [Google Scholar] [CrossRef]
- McNamara, B.; Wiesenfeld, K.; Roy, R. Observation of stochastic resonance in a ring laser. Phys. Rev. Lett. 1988, 60, 2626–2629. [Google Scholar] [CrossRef] [PubMed]
- McNamara, B.; Wiesenfeld, K. Theory of stochastic resonance. Phys. Rev. A 1989, 39, 4854–4869. [Google Scholar] [CrossRef]
- Gammaitoni, L.; Hänggi, P.; Jung, P.; Marchesoni, F. Stochastic resonance. Rev. Mod. Phys. 1998, 70, 223–287. [Google Scholar] [CrossRef]
- Hu, G. Stochastic Forces and Nonlinear System; Shanghai Science & Technology Education Press: Shanghai, China, 1994. [Google Scholar]
- Collins, J.J.; Chow, C.C.; Imhoff, T.T. Aperiodic stochastic resonance in excitable systems. Phys. Rev. E 1995, 52, R3321. [Google Scholar] [CrossRef]
- Stocks, N.G. Suprathreshold stochastic resonance in multilevel threshold systems. Phys. Rev. Lett. 2000, 84, 2310–2313. [Google Scholar] [CrossRef] [PubMed]
- Asdi, A.S.; Ahmed, H.T. Detection of weak signals using adaptive stochastic resonance. In Proceedings of the 1995 International Conference on Acoustics, Speech, and Signal Processing, Detroit, MI, USA, 9–12 May 1995. [Google Scholar] [CrossRef]
- Xu, B.H.; Duan, F.B.; Chapeau-Blondeau, F. Comparison of aperiodic stochastic resonance in a bistable system realized by adding noise and by tuning system parameters. Phys. Rev. E 2004, 69, 061110. [Google Scholar] [CrossRef] [PubMed]
- Bates, R.; Blyuss, O.; Zaikin, A. Stochastic resonance in an intracellular genetic perceptron. Phys. Rev. E 2014, 89, 032716. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.B.; Jiang, Z.P.; Xu, B.H.; Repperger, D.W. An investigation of two-dimensional parameter-induced stochastic resonance and applications in nonlinear image processing. J. Phys. A Math. Theor. 2009, 42, 145207. [Google Scholar] [CrossRef]
- Ryu, C.; Kong, S.G.; Kim, H. Enhancement of feature extraction for low-quality fingerprint images using stochastic resonance. Pattern Recognit. Lett. 2011, 32, 107–113. [Google Scholar] [CrossRef]
- Duan, F.B.; Abbott, D. Binary modulated signal detection in a bistable receiver with stochastic resonance. Physics A 2007, 376, 173–190. [Google Scholar] [CrossRef]
- Huang, Q.; Liu, J.; Li, H.W. A modified adaptive stochastic resonance for detecting faint signal in sensors. Sensors 2007, 7, 157–165. [Google Scholar] [CrossRef]
- Hu, N.Q.; Chen, M.; Wen, X.S. The application of stochastic resonance theory for early detecting rub-impact fault of rotor system. Mech. Syst. Signal Process. 2003, 17, 883–895. [Google Scholar] [CrossRef]
- Leng, Y.G.; Wang, T.Y.; Guo, Y.; Xu, Y.G.; Fan, S.B. Engineering signal processing based on bistable stochastic resonance. Mech. Syst. Signal Process. 2007, 21, 138–150. [Google Scholar] [CrossRef]
- Lu, S.L.; He, Q.B.; Zhang, H.B.; Kong, F.R. Rotating machine fault diagnosis through enhanced stochastic resonance by full-wave signal construction. Mech. Syst. Signal Process. 2017, 85, 82–97. [Google Scholar] [CrossRef]
- Leng, Y.G.; Leng, Y.S.; Wang, T.Y.; Guo, Y. Numerical analysis and engineering application of large parameter stochastic resonance. J. Sound Vib. 2006, 292, 788–801. [Google Scholar] [CrossRef]
- Yang, D.X.; Hu, Z.; Yang, Y.M. The analysis of stochastic resonance of periodic signal with large parameters. Acta Phys. Sin. 2012, 61, 080501. [Google Scholar] [CrossRef]
- Lin, M.; Huang, Y.M. Modulation and demodulation for detecting weak periodic signal of stochastic resonance. Acta Phys. Sin. 2006, 55, 3227–3282. [Google Scholar] [CrossRef]
- Tan, J.Y.; Chen, X.F.; Wang, J.Y.; Chen, H.X.; Gao, H.R. Study of frequency-shifted and re-scaling stochastic resonance and its application to fault diagnosis. Mech. Syst. Signal Process. 2009, 23, 811–822. [Google Scholar] [CrossRef]
- Xu, B.H.; Li, J.L.; Duan, F.B.; Zheng, J.Y. Effects of colored noise on multi-frequency signal processing via stochastic resonance with tuning system parameters. Chaos Solitons Fractals 2003, 16, 93–106. [Google Scholar] [CrossRef]
- Jiao, S.B.; Ren, C.; Huang, W.C.; Liang, Y.M. Parameter-induced stochastic resonance in multi-frequency weak signal detection with α stable noise. Acta Phys. Sin. 2013, 62, 210501. [Google Scholar] [CrossRef]
- Shi, P.M.; Ding, X.J.; Han, D.Y. Study on multi-frequency weak signal detection method based on stochastic resonance tuning by multi-scale noise. Measurement 2014, 47, 540–546. [Google Scholar] [CrossRef]
- Han, D.Y.; An, S.J.; Shi, P.M. Multi-frequency weak signal detection based on wavelet transform and parameter compensation band-pass multi-stable stochastic resonance. Mech. Syst. Signal Process. 2016, 70, 995–1010. [Google Scholar] [CrossRef]
- Guo, W.; Zhou, Z.M.; Chen, C.; Li, X. Multi-frequency weak signal detection based on multi-segment cascaded stochastic resonance for rolling bearings. Microelectron. Reliab. 2017, 75, 239–252. [Google Scholar] [CrossRef]
- Liu, J.J.; Leng, Y.G.; Lai, Z.H.; Tan, D. Stochastic resonance based on frequency information exchange. Acta Phys. Sin. 2016, 65, 220501. [Google Scholar] [CrossRef]
- Chen, X.H.; Cheng, G.; Shan, X.L.; Hu, X.; Guo, Q.; Liu, H.G. Research of weak fault feature information extraction of planetary gear based on ensemble empirical mode decomposition and adaptive stochastic resonance. Measurement 2015, 73, 55–67. [Google Scholar] [CrossRef]
- Leng, Y.G.; Zheng, A.Z.; Fan, S.B. SVD component-envelope detection method and its application in the incipient fault diagnosis of rolling bearing. J. Vib. Eng. 2014, 27, 794–800. [Google Scholar] [CrossRef]





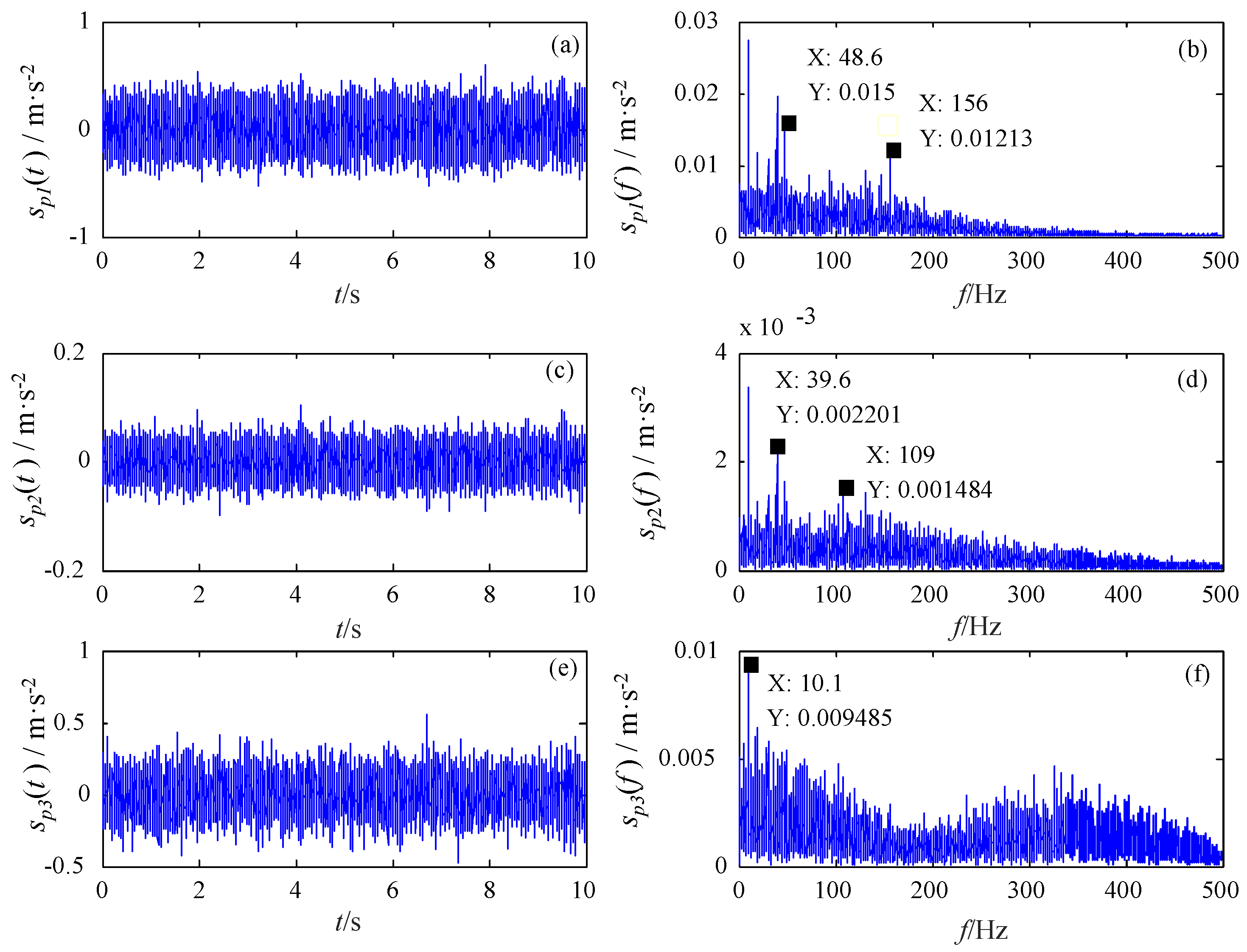
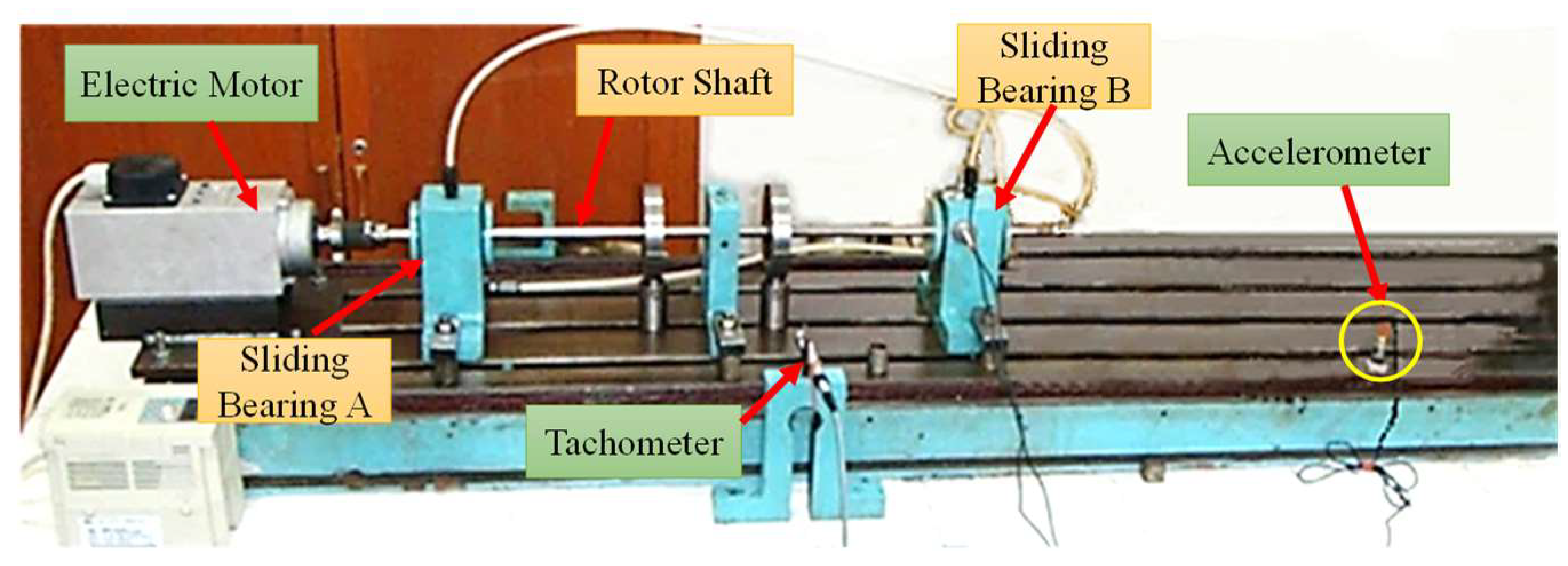

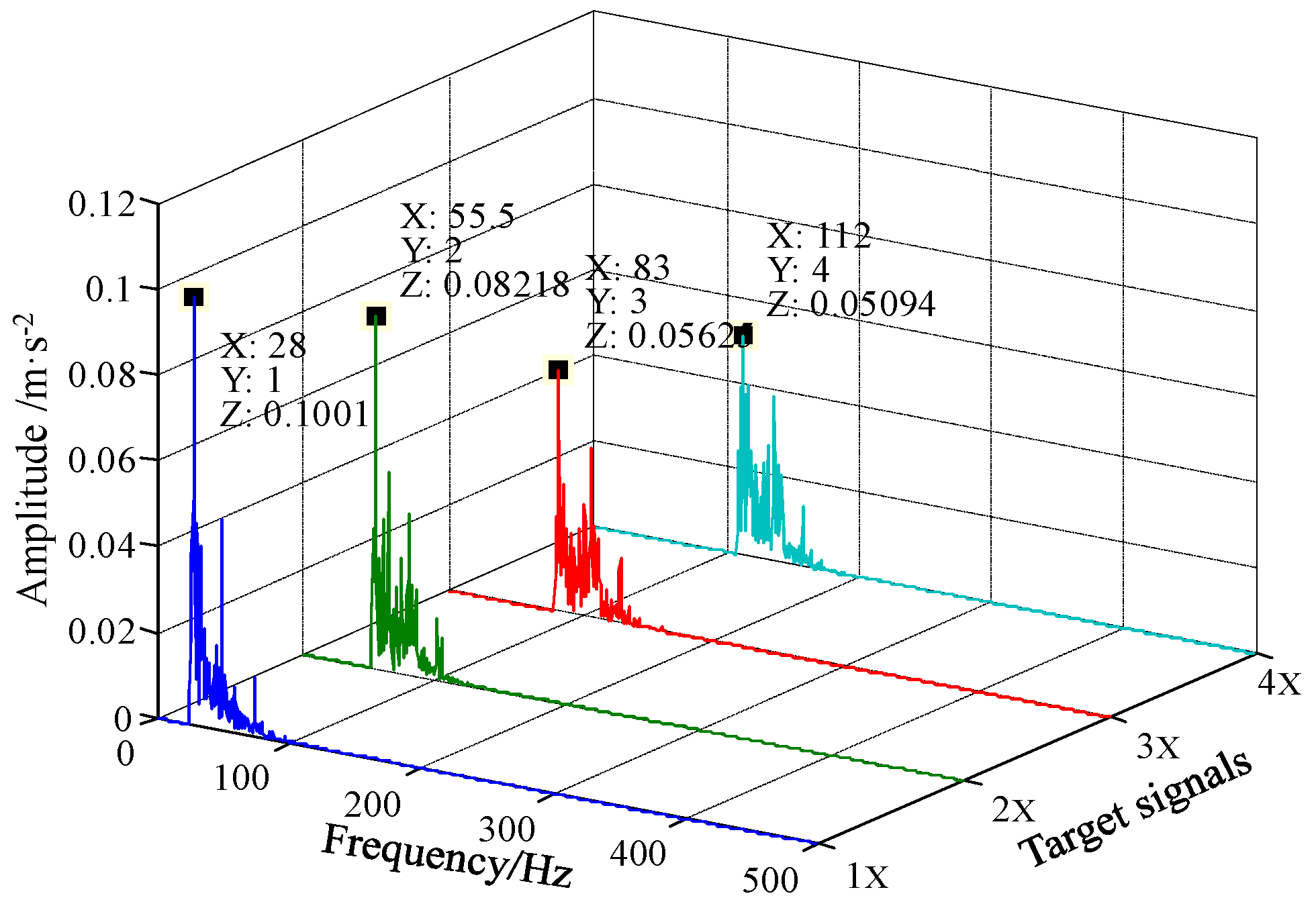
| Pitch Diameter D (mm) | Rolling Element Diameter d (mm) | Number of Rolling Elements Z | Contact Angle (°) |
|---|---|---|---|
| 185 | 25.25 | 17 | 0 |
| Methods | Frequency Detection Range |
|---|---|
| CSR | Far less than 1 Hz |
| FRSR | (0, ), is sampling frequency |
| FERSR | (0, ) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Leng, Y.; Lai, Z.; Fan, S. Multi-Frequency Signal Detection Based on Frequency Exchange and Re-Scaling Stochastic Resonance and Its Application to Weak Fault Diagnosis. Sensors 2018, 18, 1325. https://doi.org/10.3390/s18051325
Liu J, Leng Y, Lai Z, Fan S. Multi-Frequency Signal Detection Based on Frequency Exchange and Re-Scaling Stochastic Resonance and Its Application to Weak Fault Diagnosis. Sensors. 2018; 18(5):1325. https://doi.org/10.3390/s18051325
Chicago/Turabian StyleLiu, Jinjun, Yonggang Leng, Zhihui Lai, and Shengbo Fan. 2018. "Multi-Frequency Signal Detection Based on Frequency Exchange and Re-Scaling Stochastic Resonance and Its Application to Weak Fault Diagnosis" Sensors 18, no. 5: 1325. https://doi.org/10.3390/s18051325
APA StyleLiu, J., Leng, Y., Lai, Z., & Fan, S. (2018). Multi-Frequency Signal Detection Based on Frequency Exchange and Re-Scaling Stochastic Resonance and Its Application to Weak Fault Diagnosis. Sensors, 18(5), 1325. https://doi.org/10.3390/s18051325





