A Capsule-Type Electromagnetic Acoustic Transducer for Fast Screening of External Corrosion in Nonmagnetic Pipes
Abstract
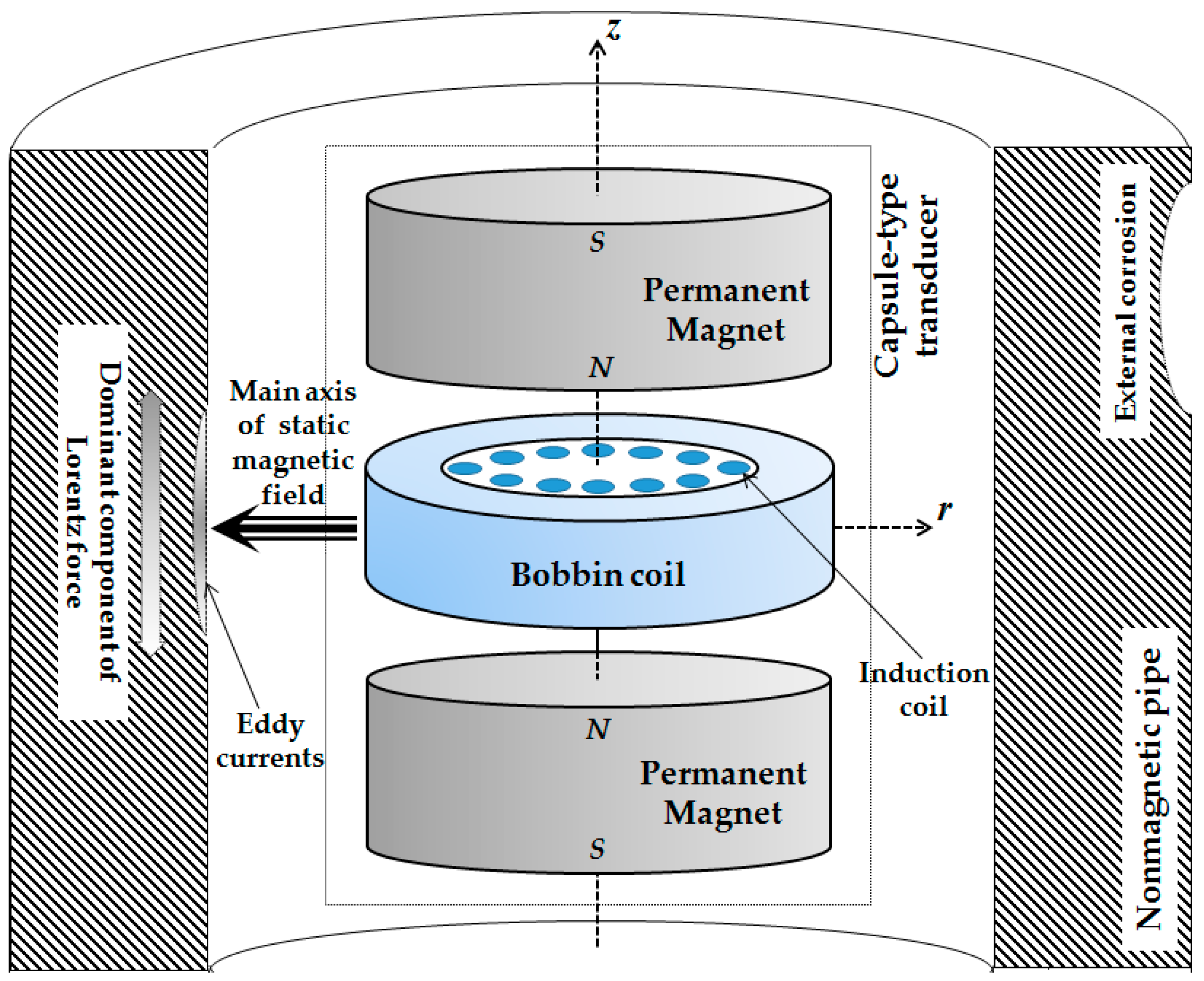
:1. Introduction
2. 3D Hybrid Model of the Proposed Transducer
2.1. Static Magnetic Field
2.2. Dynamic Electromagnetic Field
2.3. Lorentz Force
2.4. EMF Signals
3. Corroboration and Simulations
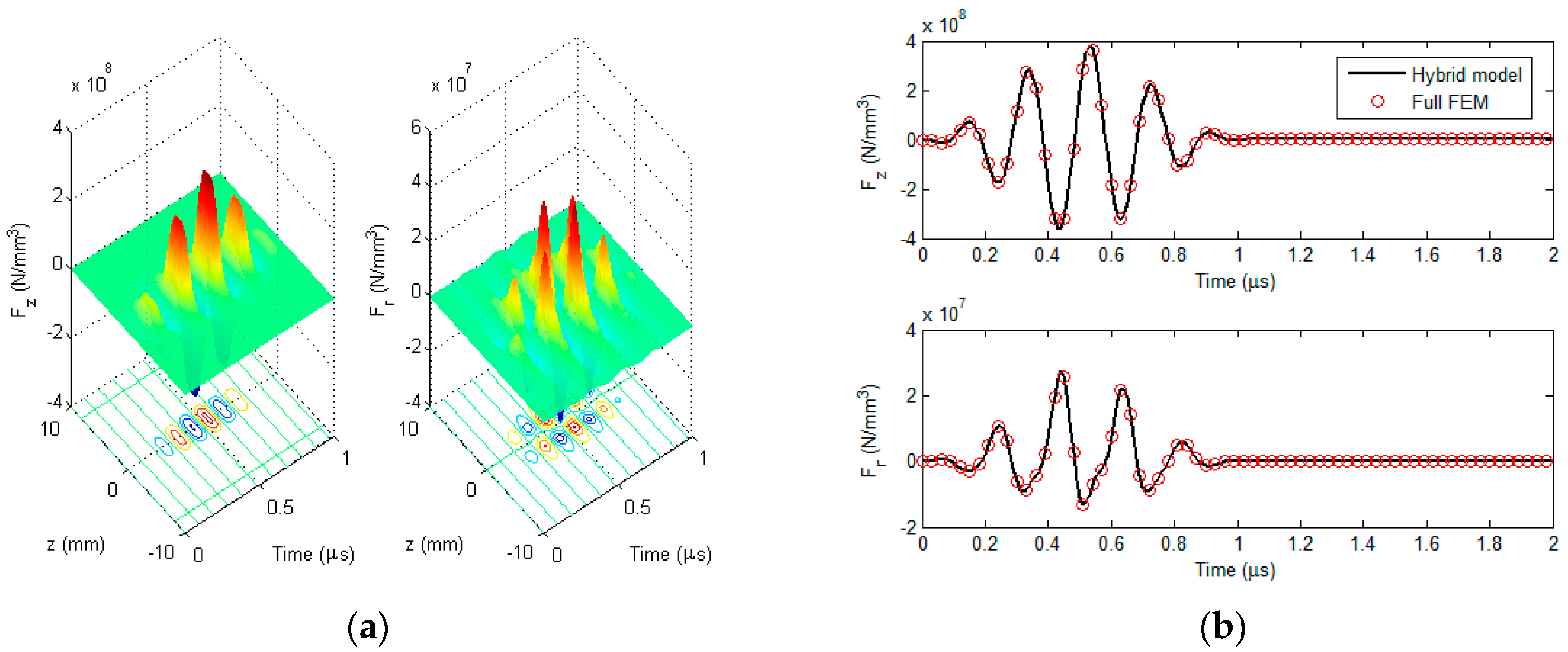
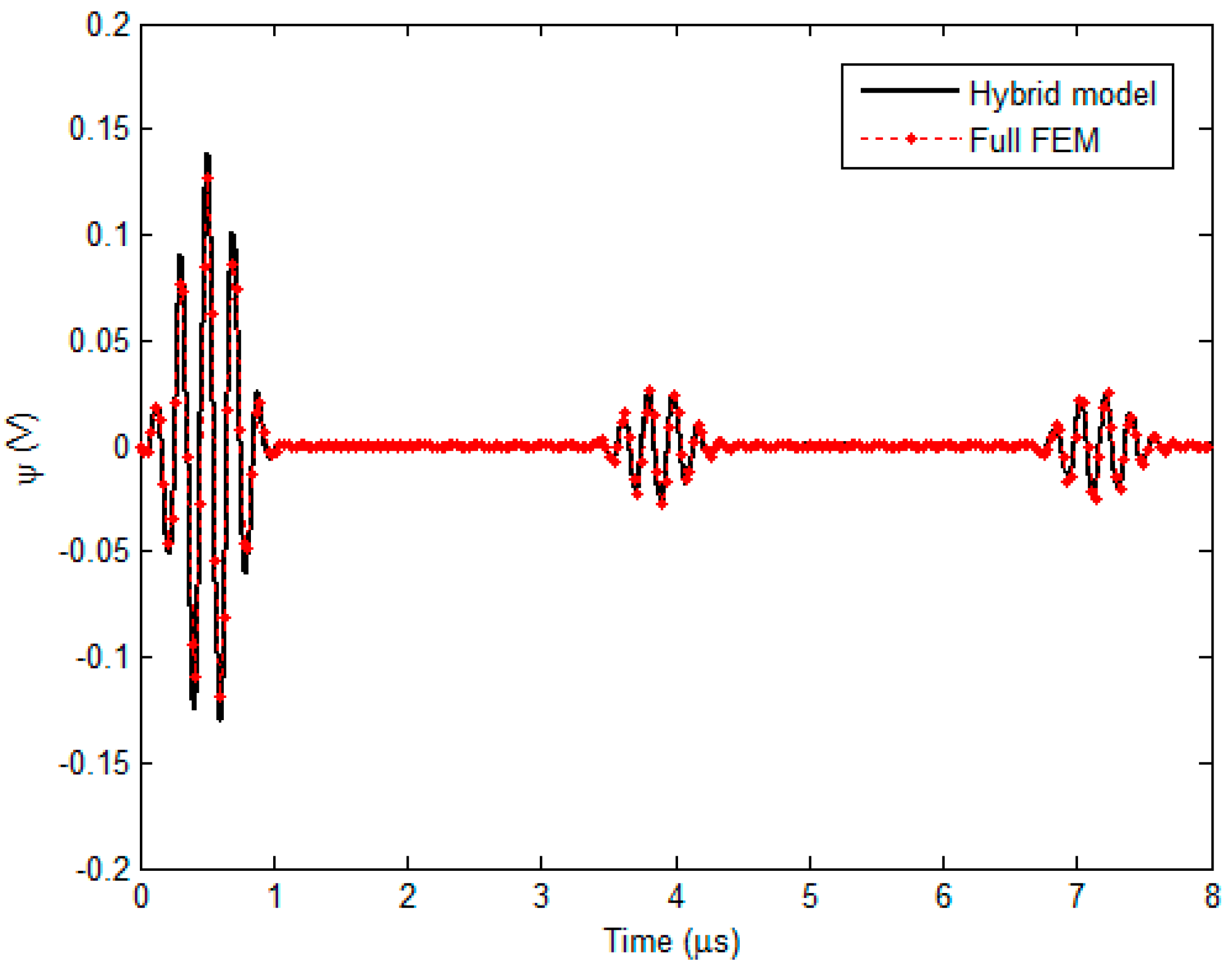
3.1. Verification of the Hybrid Model
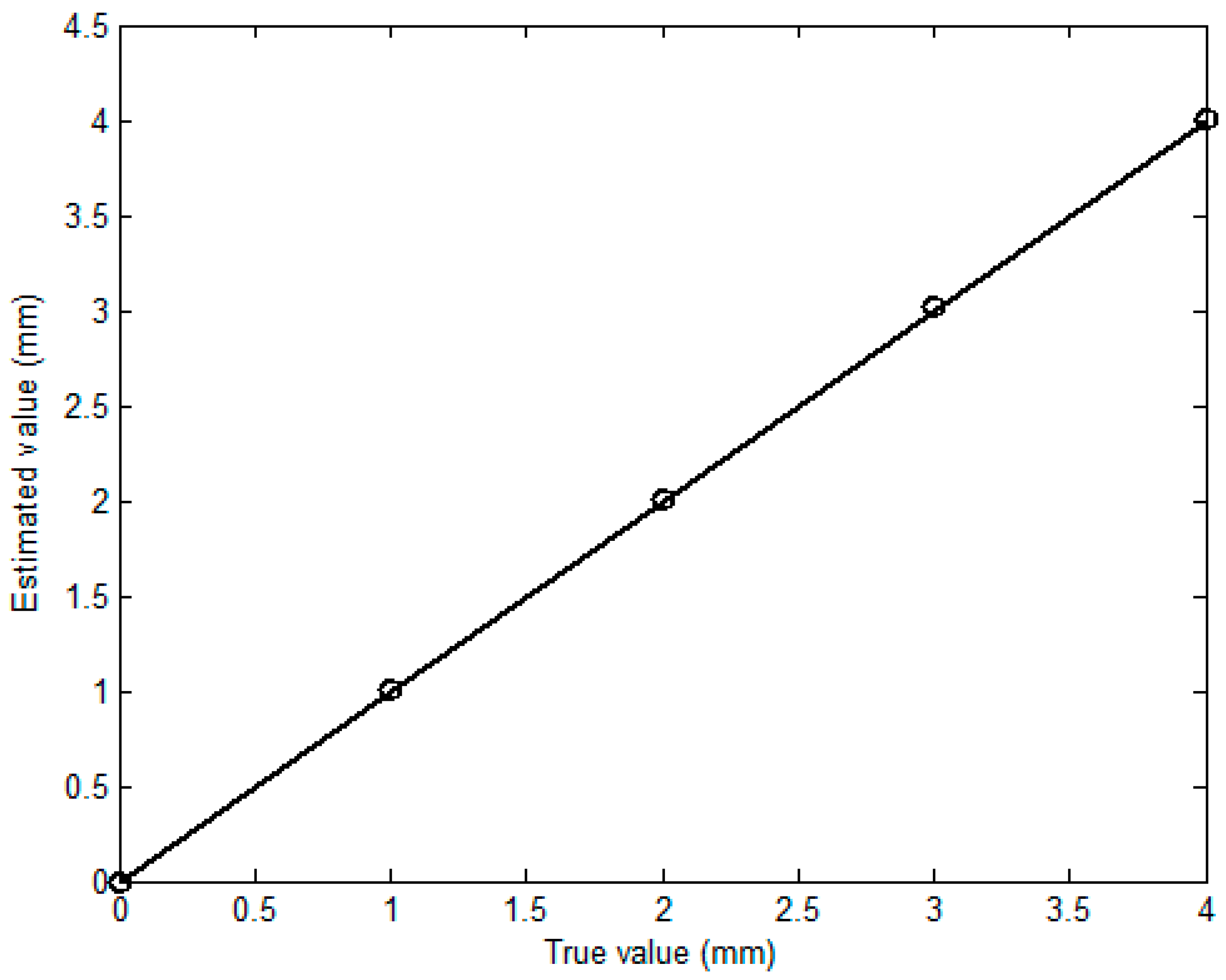
3.2. Simulations with External Corrosion
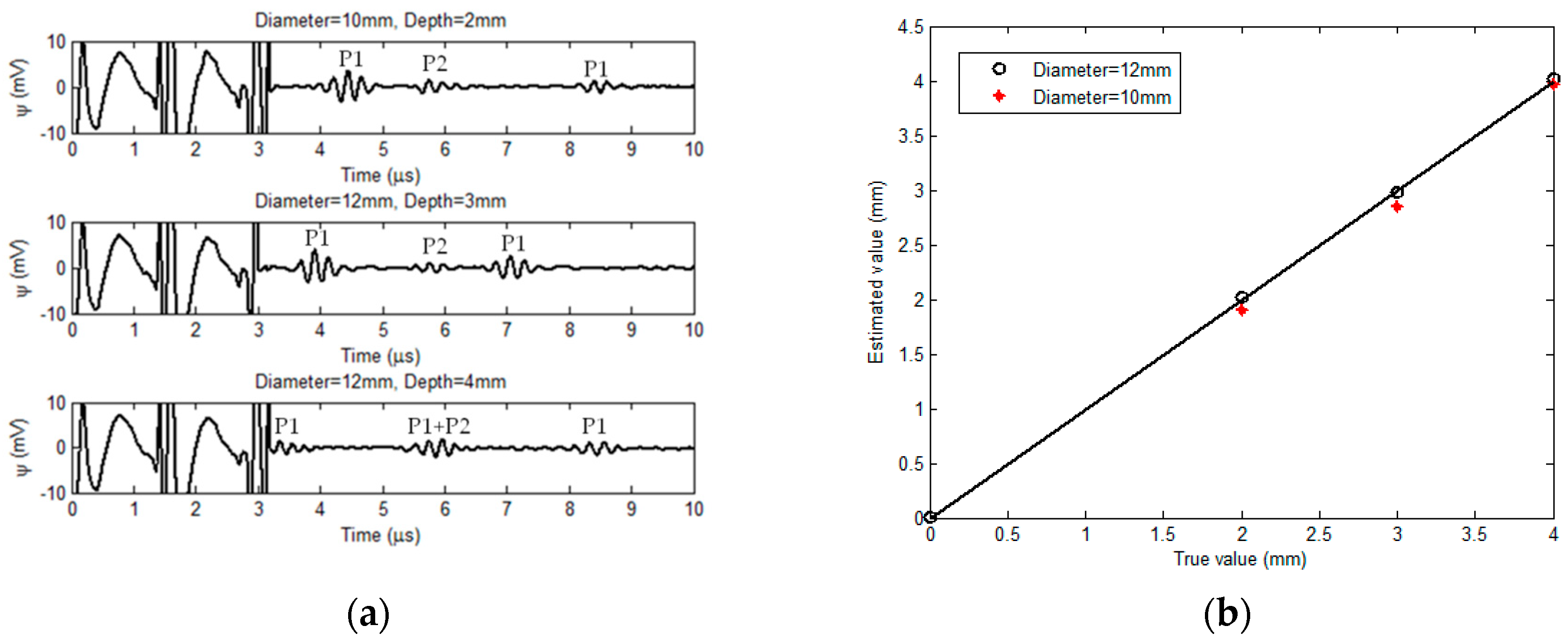
4. Experiments
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Machado, M.; Rosado, L.; Pedrosa, N.; Vostner, A.; Miranda, R.M.; Piedade, M.; Santos, T.G. Novel Eddy Current Probes for Pipes: Application in Austenitic Round-in-square Profiles of ITER. NDT E Int. 2017, 87, 111–118. [Google Scholar] [CrossRef]
- Mao, X.; Lei, Y. Thickness Measurement of Metal Pipe Using Swept-frequency Eddy Current Testing. NDT E Int. 2016, 78, 10–19. [Google Scholar] [CrossRef]
- Rakvin, M.; Markucic, D.; Hizman, B. Evaluation of Pipe Wall Thickness Based on Contrast Measurement Using Computed Radiography (CR). Procedia Eng. 2014, 69, 1216–1224. [Google Scholar] [CrossRef]
- Lai, S.; Chen, D.Y.; Chen, H.; Fu, Y.W. Pulsed Eddy Current Testing of Inner Wall Flaws in Pipe under Insulation. Procedia Eng. 2015, 130, 1658–1664. [Google Scholar] [CrossRef]
- Shih, J.L.; Wu, K.T.; Jen, C.K.; Chiu, C.H.; Tzeng, J.C.; Liaw, J.W. Applications of Flexible Ultrasonic Transducer Array for Defect Detection at 150 °C. Sensors 2013, 13, 975–983. [Google Scholar] [CrossRef] [PubMed]
- Predoi, M.; Petre, C. Thin Wall Pipe Ultrasonic Inspection through Paint Coating. Phys. Procedia 2015, 70, 287–291. [Google Scholar] [CrossRef]
- Cheong, Y.; Kim, K.; Kim, D. High-temperature Ultrasonic Thickness Monitoring for Pipe Thinning in a Flow-accelerated Corrosion Proof Test Facility. Nuclear Eng. Technol. 2017, 49, 1463–1471. [Google Scholar] [CrossRef]
- Hirao, M.; Ogi, H. EMATs for Science and Industry: Noncontacting Ultrasonic Measurements; Kluwer Academic: Boston, MA, USA, 2003; ISBN 1-4020-7494-8. [Google Scholar]
- Lunn, N.; Dixon, S.; Potter, G. High Temperature EMAT Design for Scanning or Fixed Point Operation on Magnetite Coated Steel. NDT E Int. 2017, 89, 74–80. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, X.; Sun, P.; Li, J. Enhancement of the Excitation Efficiency of a Torsional Wave PPM EMAT Array for Pipe Inspection by Optimizing the Element Number of the Array Based on 3-D FEM. Sensors 2015, 15, 3471–3490. [Google Scholar] [CrossRef] [PubMed]
- Pei, C.X.; Xiao, P.; Zhao, S.Q.; Chen, Z.M. Development of a Flexible Film Electromagnetic Acoustic Transducer for Nondestructive Testing. Sens. Actuator A-Phys. 2017, 258, 68–73. [Google Scholar] [CrossRef]
- Song, X.; Qiu, G. Optimization of a Focusable and Rotatable Shear-Wave Periodic Permanent Magnet Electromagnetic Acoustic Transducers for Plates Inspection. Sensors 2017, 17, 2722. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Yin, L.; Rodriguez, S.G.; Yang, T.; Liu, Z.; Yin, W. A Wholly Analytical Method for the Simulation of an Electromagnetic Acoustic Transducer Array. Int. J. Appl. Electromagn. Mech 2016, 51, 1–15. [Google Scholar] [CrossRef]
- Yin, W.; Xie, Y.; Qu, Z.; Liu, Z. A Pseudo-3D Model for Electromagnetic Acoustic Transducers (EMATs). Appl. Sci. 2018, 8, 450. [Google Scholar] [CrossRef]
- Xie, Y.; Rodriguez, S.G.; Zhang, W.; Liu, Z.; Yin, W. Simulation of an Electromagnetic Acoustic Transducer Array by using Analytical Method and FDTD. J. Sens. 2016, 5451821. [Google Scholar] [CrossRef]
- Li, Y.; Theodoulidis, T.; Tian, G.Y. Magnetic Field-based Eddy-current Modeling for Multilayered Specimens. IEEE Trans. Magn 2007, 43, 4010–4015. [Google Scholar] [CrossRef]
- Li, Y.; Liu, X.B.; Chen, Z.M.; Zhao, H.D.; Cai, W.L. A Fast Forward Model of Pulsed Eddy Current Inspection of Multilayered Tubular Structures. Int. J. Appl. Electromagn. Mech. 2014, 45, 417–423. [Google Scholar] [CrossRef]
- Li, Y.; Yan, B.; Li, W.J.; Jing, H.Q.; Chen, Z.M.; Li, D. Pulse-modulation Eddy Current Probes for Imaging of External Corrosion in Nonmagnetic Pipes. NDT E Int. 2017, 88, 51–58. [Google Scholar] [CrossRef]
- Ravaud, R.; Lemarquand, G.; Babic, S.; Lemarquand, V.; Akyel, C. Cylindrical Magnets and Coils: Fields, Forces and Inductances. IEEE Trans. Magn. 2010, 46, 3585–3590. [Google Scholar] [CrossRef]
- Li, Y.; Tian, G.Y.; Simm, A. Fast Analytical Modelling for Pulsed Eddy Current Evaluation. NDT E Int. 2008, 41, 477–483. [Google Scholar] [CrossRef]
- Bowler, J.R.; Theodoulidis, T.P. Eddy Currents Induced in a Conducting Rod of Finite Length by a Coaxial Encircling Coil. J. Phys. D-Appl. Phys. 2005, 38, 2861–2868. [Google Scholar] [CrossRef]
- Cao, B.H.; Li, C.; Fan, M.B.; Ye, B.; Gao, S. Analytical Modelling of Eddy Current Response from Driver Pick-up Coils on Multi-layered Conducting Plates. Insight 2018, 60, 77–83. [Google Scholar] [CrossRef]
- Li, Y.; Chen, M.; Qi, Y. Generalized Analytical Expressions of Liftoff Intersection in PEC and a Liftoff-intersection-based Fast Inverse Model. IEEE Trans. Magn. 2011, 47, 2931–2934. [Google Scholar] [CrossRef]
- Xie, S.J.; Chen, Z.M.; Takagi, T.; Uchimoto, T. Quantitative Non-destructive Evaluation of Wall Thinning Defect in Double-layer Pipe of Nuclear Power Plants Using Pulsed ECT Method. NDT E Int. 2015, 75, 87–95. [Google Scholar] [CrossRef]

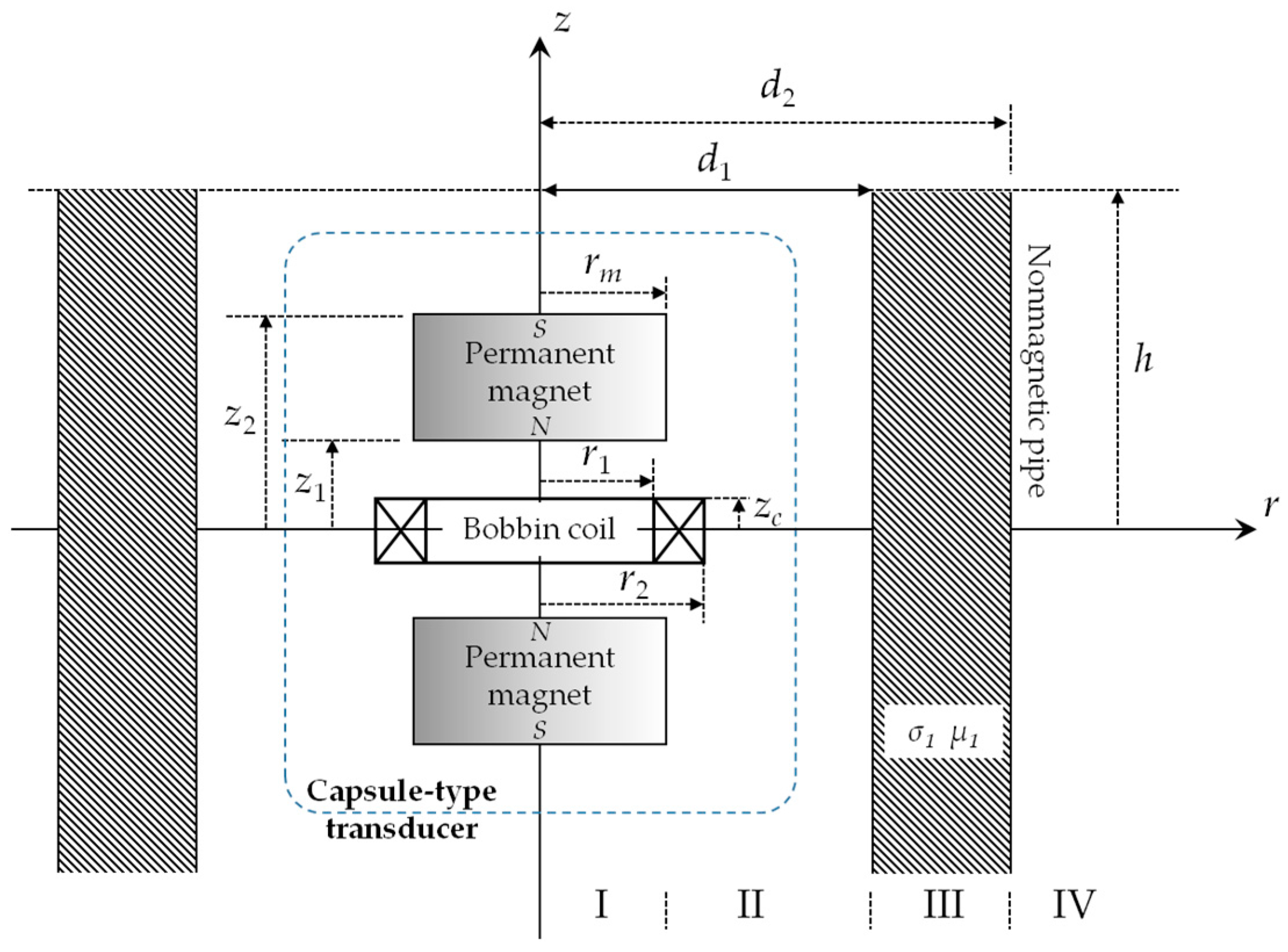
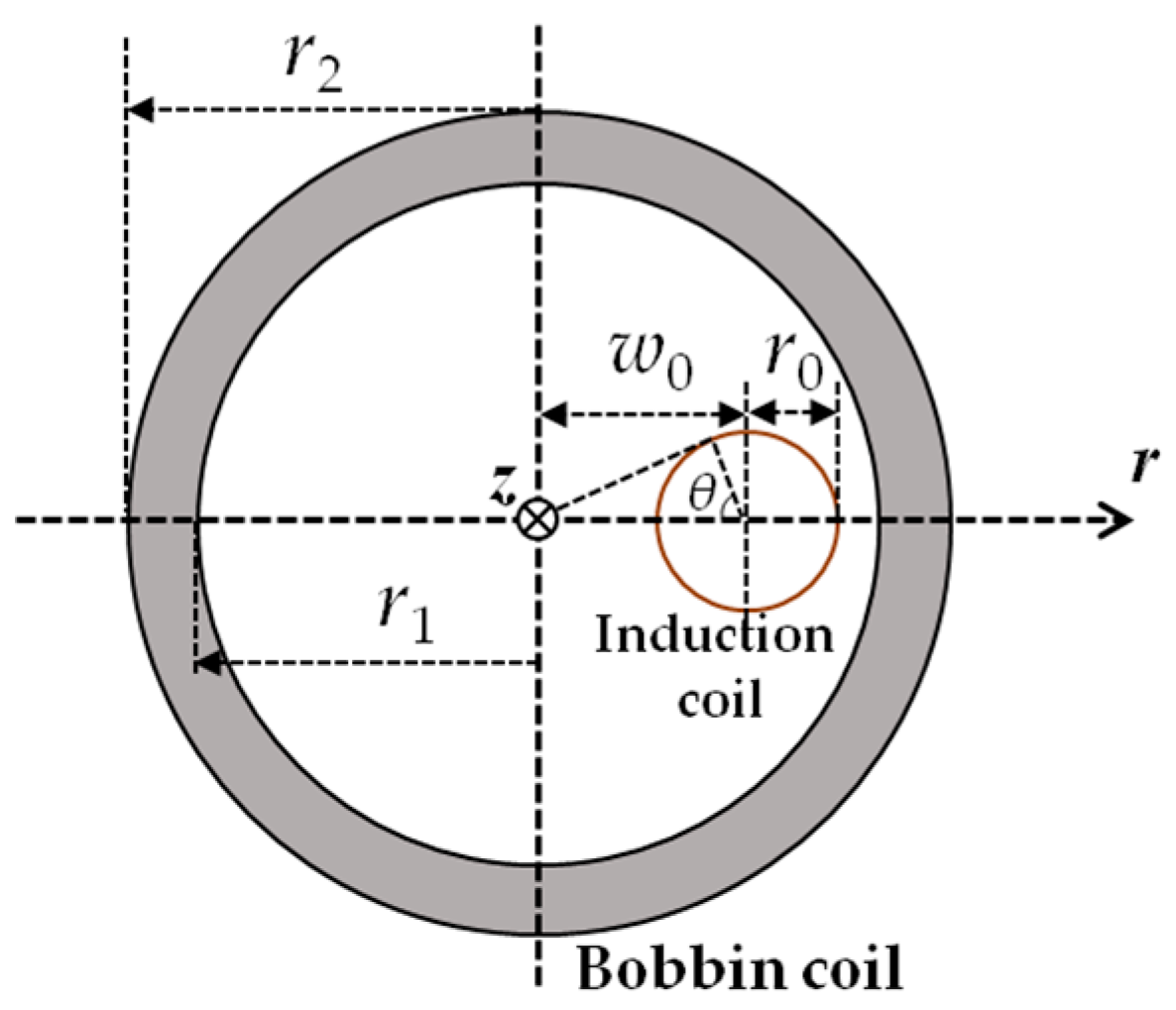




| Transducer Parameter | Value |
|---|---|
| Remanence field of the magnet, Brem (T) | 1.47 |
| Position of the magnet upper surface, z1 (mm) | 2.0 |
| Magnet height, z2 − z1 (mm) | 5.0 |
| Magnet Radius, rm (mm) | 15.0 |
| Inner radius of the bobbin coil, r1 (mm) | 15.4 |
| Outer radius of the bobbin coil, r2 (mm) | 15.6 |
| Height of the bobbin coil, 2zc (mm) | 3.0 |
| Number of turns of the bobbin coil, N | 32 |
| Radius of the induction coil, r0 (mm) | 2.0 |
| Height of the induction coil, zin (mm) | 3.0 |
| Number of turns of the induction coil, Nin | 30 |
| Distance between the centers of the bobbin coil and induction coil, w0 (mm) | 13.3 |
| Liftoff distance, d1 − r2 (mm) | 0.4 |
| Pipe Parameter | Value |
|---|---|
| Inner radius, d1 (mm) | 16.0 |
| Outer radius, d2 (mm) | 22.0 |
| Conductivity, σ1 (MS·m−1) | 34.2 |
| Relative permeability, μ1 | 1.0 |
| Young’s modulus (GPa) | 71.7 |
| Density (kg·m−3) | 2750 |
| Poisson’s ratio | 0.33 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Cai, R.; Yan, B.; Zainal Abidin, I.M.; Jing, H.; Wang, Y. A Capsule-Type Electromagnetic Acoustic Transducer for Fast Screening of External Corrosion in Nonmagnetic Pipes. Sensors 2018, 18, 1733. https://doi.org/10.3390/s18061733
Li Y, Cai R, Yan B, Zainal Abidin IM, Jing H, Wang Y. A Capsule-Type Electromagnetic Acoustic Transducer for Fast Screening of External Corrosion in Nonmagnetic Pipes. Sensors. 2018; 18(6):1733. https://doi.org/10.3390/s18061733
Chicago/Turabian StyleLi, Yong, Rui Cai, Bei Yan, Ilham Mukriz Zainal Abidin, Haoqing Jing, and Yi Wang. 2018. "A Capsule-Type Electromagnetic Acoustic Transducer for Fast Screening of External Corrosion in Nonmagnetic Pipes" Sensors 18, no. 6: 1733. https://doi.org/10.3390/s18061733
APA StyleLi, Y., Cai, R., Yan, B., Zainal Abidin, I. M., Jing, H., & Wang, Y. (2018). A Capsule-Type Electromagnetic Acoustic Transducer for Fast Screening of External Corrosion in Nonmagnetic Pipes. Sensors, 18(6), 1733. https://doi.org/10.3390/s18061733






