Study on the Optimal Groove Shape and Glue Material for Fiber Bragg Grating Measuring Bolts
Abstract
:1. Introduction
2. Tensile Tests on Bolts with Different Groove Shapes
2.1. Tensile Test Conditions
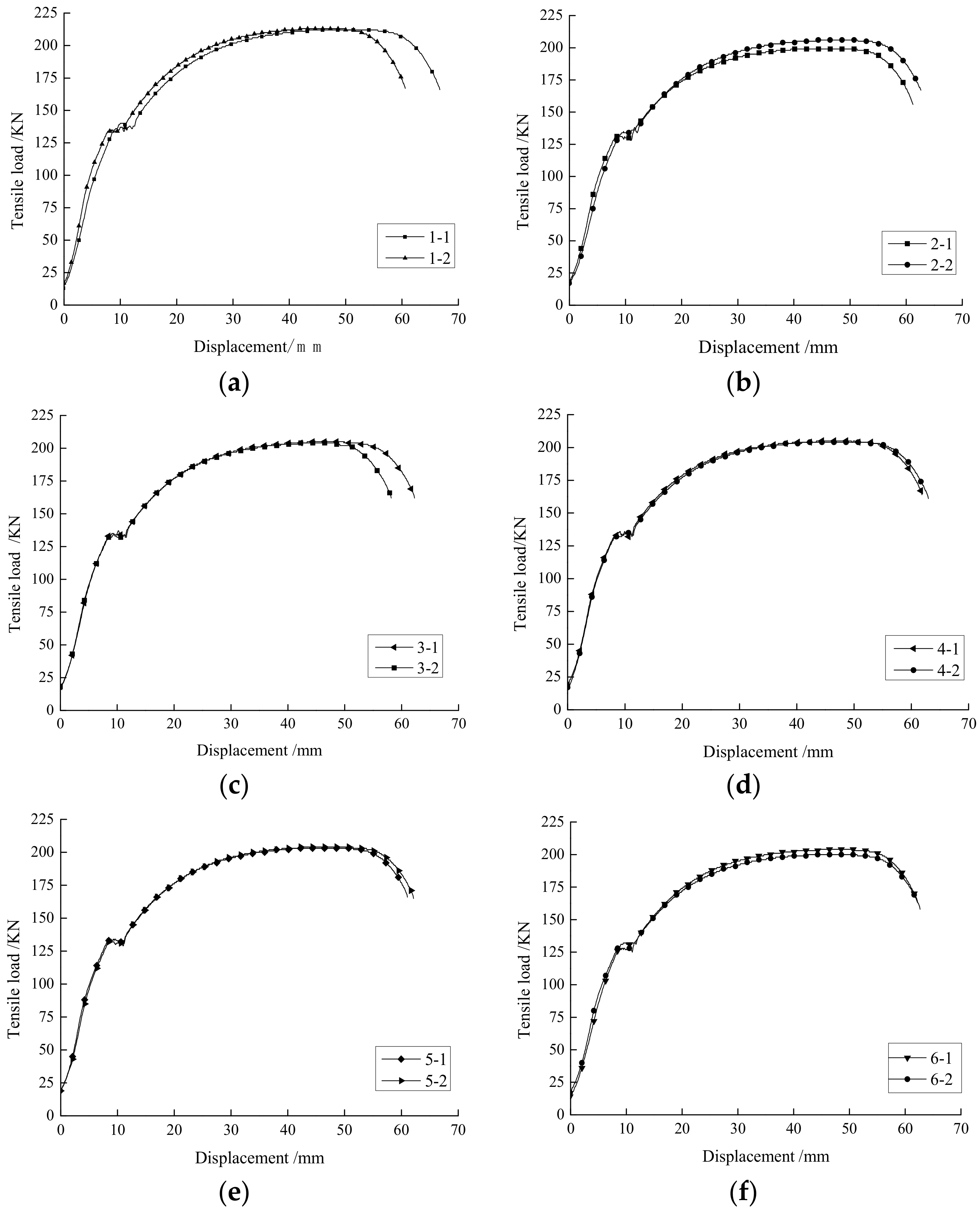
2.2. Test Procedure and Results Analysis
3. Numerical Analysis of Stress Distribution of Bonded Bolts with Different Groove Shapes
3.1. Model Geometry and Boundary Condition
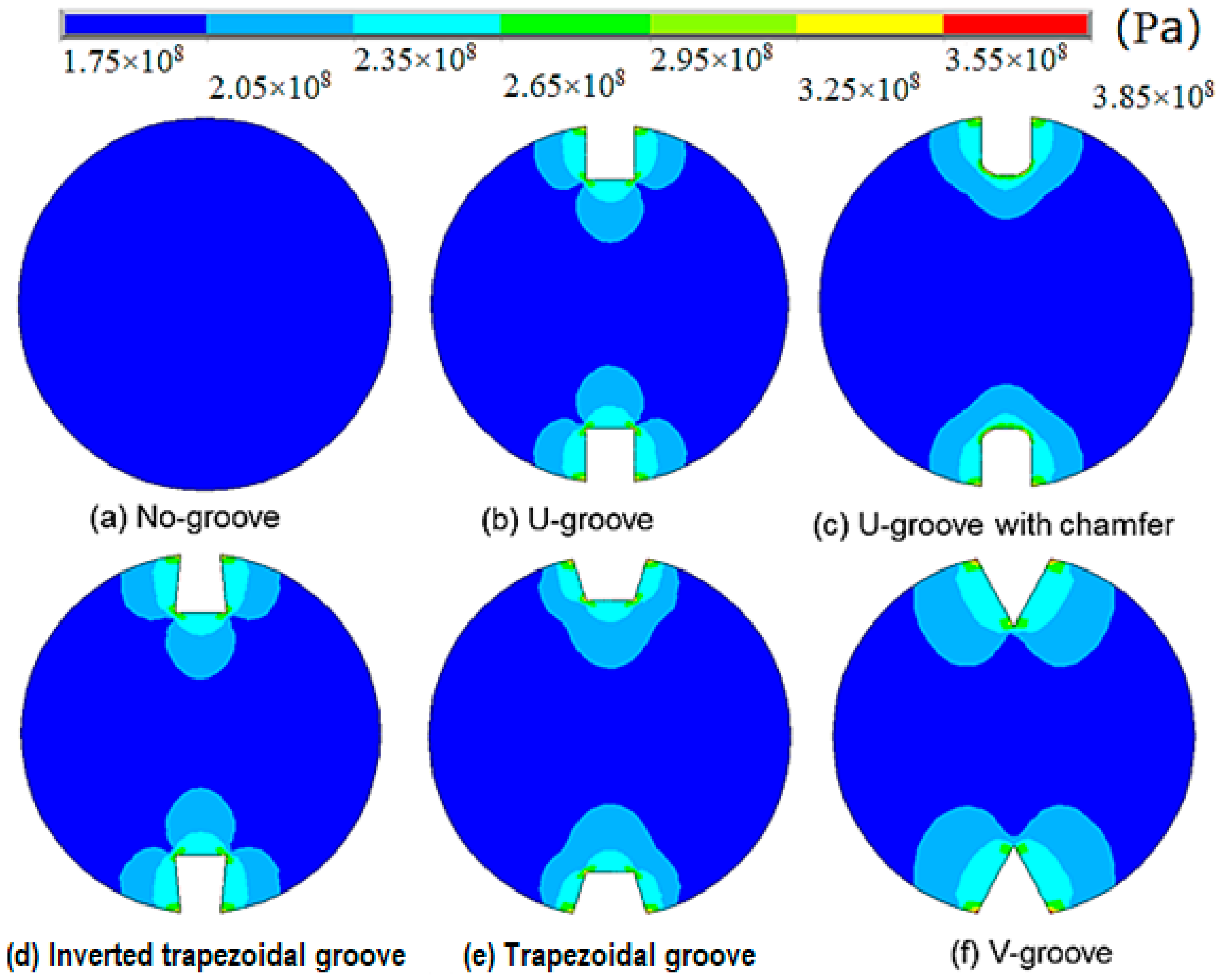
3.2. Simulation Results
4. Glue Material Recommendation
4.1. Glue Materials
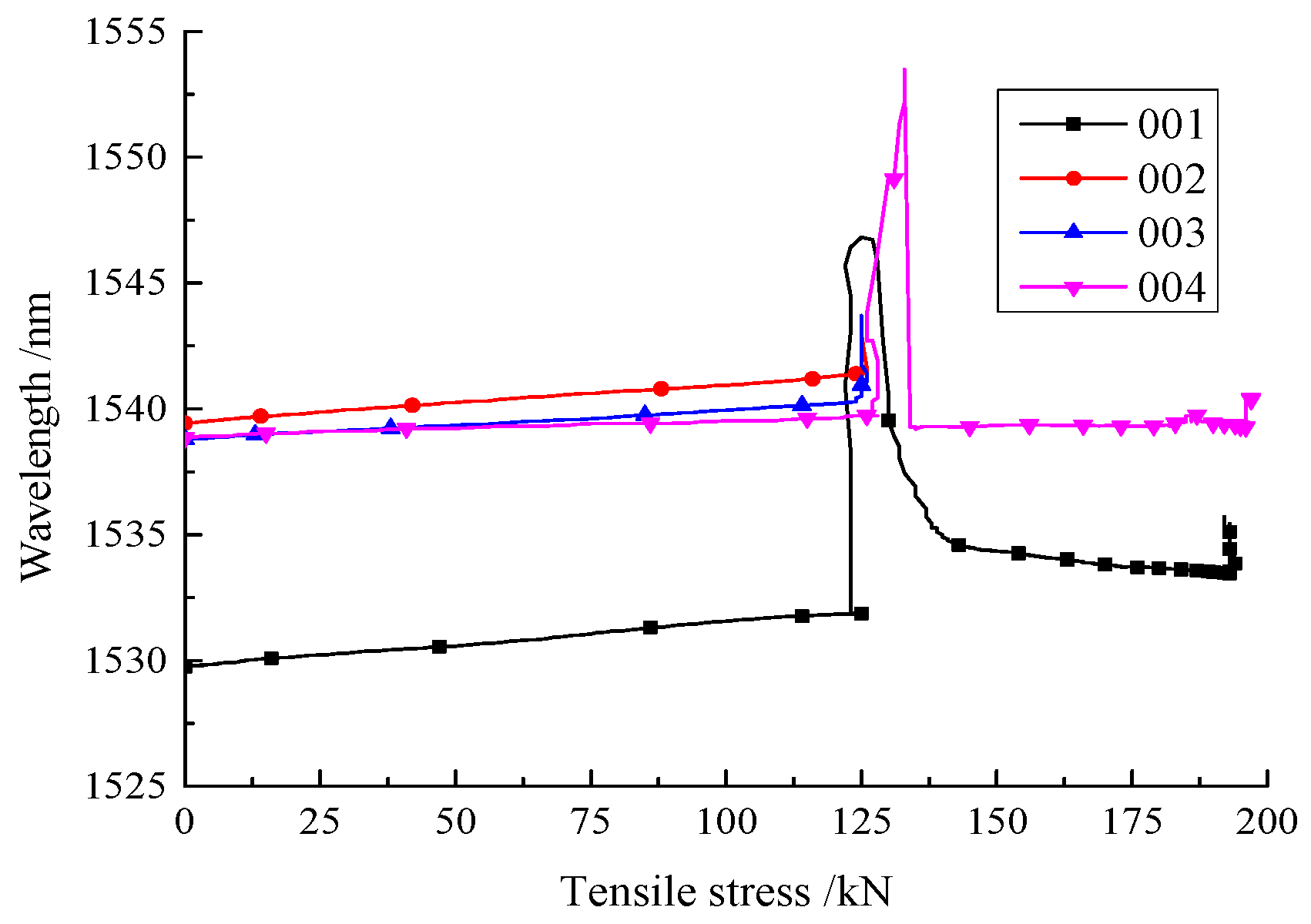
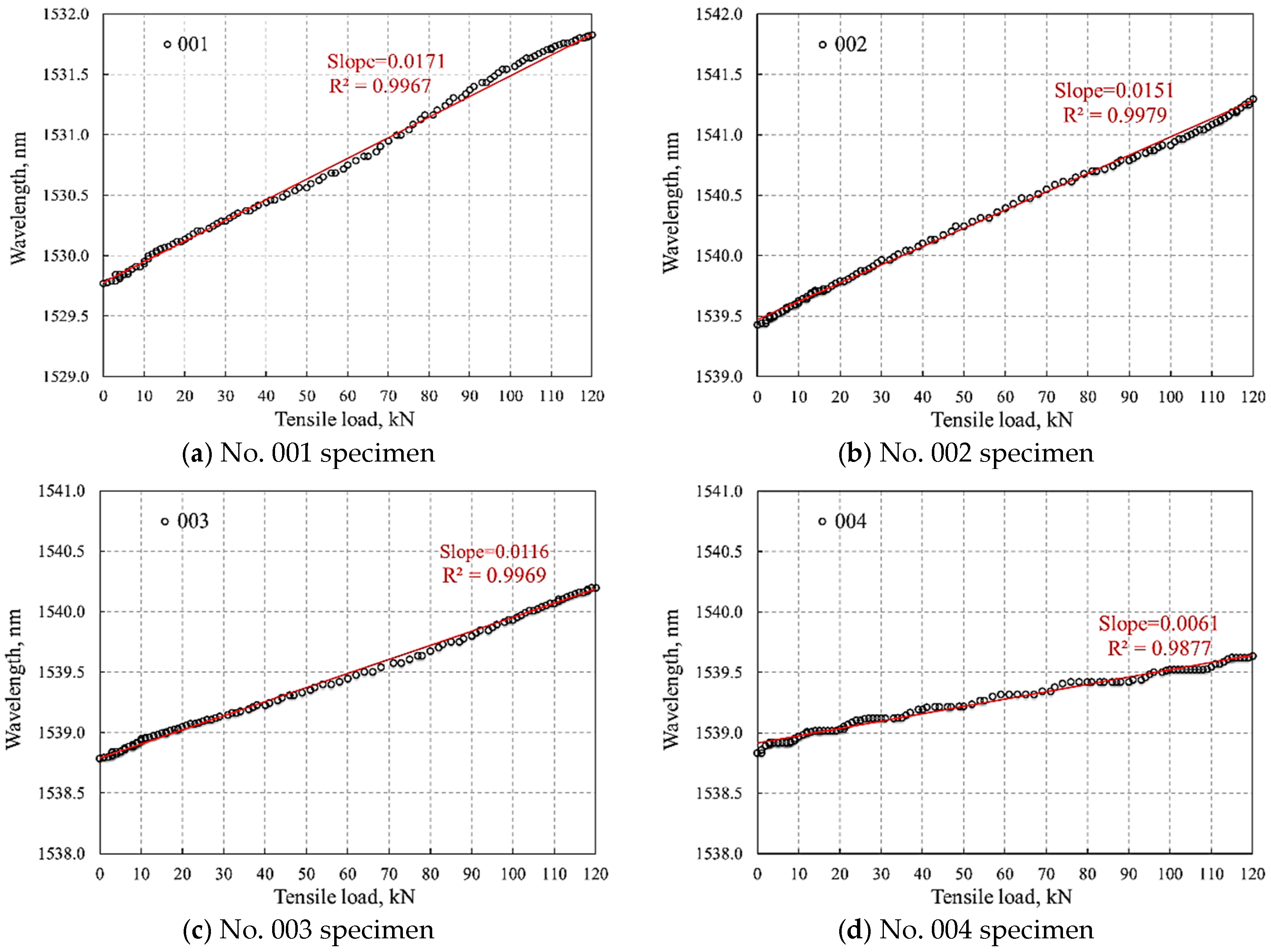
4.2. Tensile Test and Data Analysis
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Cai, Y.; Esaki, T.; Jiang, Y.J. An analytical model to predict axial load in grouted rock bolt for soft rock. Tunn. Undergr. Space Technol. 2004, 19, 607–618. [Google Scholar] [CrossRef]
- Ghadimi, M.; Shahriar, K.; Jalalifar, H. A new analytical solution for the displacement of fully grouted rock bolt in rock joints and experimental and numerical verifications. Tunn. Undergr. Space Technol. 2015, 50, 143–151. [Google Scholar] [CrossRef]
- Kang, H.; Wu, Y.; Gao, F.; Jiang, P.; Cheng, P.; Meng, X.; Li, Z. Mechanical performances and stress states of rock bolts under varying loading conditions. Tunn. Undergr. Space Technol. 2016, 52, 138–146. [Google Scholar] [CrossRef]
- Li, C.C.; Kristjansson, G.; Høien, A.H. Critical embedment length and bond strength of fully encapsulated rebar rockbolts. Tunn. Undergr. Space Technol. 2016, 59, 16–23. [Google Scholar] [CrossRef]
- Pan, C.; Yamaguchi, T.; Suzuki, Y. Evaluation of the Bolt Axial Force in High Strength Bolted Joints by Using Strain Gauges; Memoirs of the Faculty of Engineering, Osaka City University: Osaka, Japan, 2011; Volume 52, pp. 37–41. [Google Scholar]
- Starikova, R.; Schön, J.J. Experimental study on fatigue resistance of composite joints with protruding-head bolts. Compos. Struct. 2002, 55, 1–11. [Google Scholar] [CrossRef]
- Mucho, T.P.; Mark, C.; Zelenko, J.C.; Compton, C.S. Roof Support Performance in High Stress Conditions; West Virginia University: Morgantown, WV, USA, 1995. [Google Scholar]
- Xue, Y.H.; Chen, Y. Application of Vibrating Wire sensors in Dam Safety. Autom. Water Resour. Hydrol. 2006, 4, 39–42. [Google Scholar]
- Wu, Z.G.; Ju, W.J. Research and application of new dynamometer for anchor or bolt. Coal Sci. Technol. 2007, 11, 36–38. [Google Scholar]
- Beard, M.D.; Lowe, M.J.S. Non-destructive testing of rock bolts using guided ultrasonic waves. Int. J. Rock Mech. Min. Sci. 2003, 40, 527–536. [Google Scholar] [CrossRef]
- Lee, I.M.; Han, S.I.; Kim, H.; Yu, J.D.; Min, B.K.; Lee, B.K. Evaluation of rock bolt integrity using Fourier and wavelet transforms. Tunn. Undergr. Space Technol. 2012, 28, 304–314. [Google Scholar] [CrossRef]
- Si, G.; Durucan, S.; Jamnikar, S.; Lazar, J.; Abraham, K.; Korre, A.; Shi, J.Q.; Zavšek, S.; Mutke, G.; Lurka, A. Seismic monitoring and analysis of excessive gas emissions in heterogeneous coal seams. Int. J. Coal Geol. 2015, 149, 41–54. [Google Scholar] [CrossRef] [Green Version]
- Staveley, C. Get smart, go optical: Example uses of optical fibre sensing technology for production optimisation and subsea asset monitoring. In Proceedings of the Fiber Optic Sensors and Applications XI, Baltimore, MD, USA, 18 June 2014; Volume 9098. [Google Scholar]
- Zhao, Y.M.; Zhang, N.; Si, G.Y. A Fiber Bragg Grating-Based Monitoring System for Roof Safety Control in Underground Coal Mining. Sensors 2016, 16, 1759. [Google Scholar] [CrossRef] [PubMed]
- Schmidt-Hattenberger, C.; Borm, G. Bragg grating extensometer rods (BGX) for geotechnical strain measurements. In Proceedings of the European Workshop on Optical Fibre Sensors, Peebles, UK, 18 June 1998; Volume 3483, pp. 214–217. [Google Scholar]
- Lin, C.N.; Liu, Q.S.; Gao, W. Application of fiber optical sensing technology to monitoring axial forces of anchor bolts. Rock Soil Mech. 2008, 11, 3161–3164. [Google Scholar]
- Chai, J.; Zhao, W.H.; Li, Y.; Wang, D.C.; Cui, C. Pull out tests of figer Bragg grating sensor fitted bolts. J. China Univ. Min. Technol. 2012, 41, 719–724. [Google Scholar]
- Weng, X.L.; Ma, H.H.; Wang, J. Stress Monitoring for Anchor Rods System in Subway Tunnel Using FBG Technology. Adv. Mater. Sci. Eng. 2015, 2015, 1–7. [Google Scholar] [CrossRef]
- Zhu, H.H.; Yin, J.H.; Zhang, L.; Jin, W.; Dong, J.H. Monitoring Internal Displacements of a Model Dam Using FBG Sensing Bars. Adv. Struct. Eng. 2010, 13, 249–261. [Google Scholar] [CrossRef]
- Schroeck, M.; Ecke, W.; Graupner, A. Strain monitoring in steel rock bolts using FBG sensor arrays. In Proceedings of the International Society for Optical Engineering, Applications of Optical Fiver Sensor, Glasgow, UK, 31 August 2000; Volume 4074, pp. 298–304. [Google Scholar]
- Huang, M.; Zhou, Z.; Huang, Y.; Ou, J. A distributed self-sensing FRP anchor rod with built-in optical fiber sensor. Measurement 2013, 46, 1363–1370. [Google Scholar] [CrossRef]
- De Waele, W.; Moerman, W.; Taerwe, L.; Degrieck, J.; Himpe, J. Measuring ground anchor forces of a quay wall with Bragg sensors. J. Struct. Eng. 2005, 123, 322–328. [Google Scholar]
- Kim, J.M.; Kim, H.W.; Park, Y.H.; Yang, I.H.; Kim, Y.S. FBG Sensors Encapsulated into 7-Wire Steel Strand for Tension Monitoring of a Prestressing Tendon. Adv. Struct. Eng. 2012, 15, 907–917. [Google Scholar] [CrossRef]
- Do, T.M.; Kim, Y.S. Prediction of load transfer depth for cost-effective design of ground anchors using FBG sensors embedded tendon and numerical analysis. Geomech. Eng. 2016, 10, 737–755. [Google Scholar] [CrossRef]
- Xu, G.Q.; Xiong, D.Y.; Duan, Y.; Cao, X.S. Open pit slope deformation monitoring by fiber Bragg grating sensors. Opt. Eng. 2014, 54, 011003–011008. [Google Scholar] [CrossRef]
- Chen, W.M.; Zhang, P.; Wu, J.; Liu, L.H. Embedding technology of Fiber Bragg Grating strain sensor for cable tension monitor. In Proceedings of the International Conference on Optical Instruments and Technology: Optical Sensors and Applications, Beijing, China, 20 December 2013; Volume 9044. [Google Scholar]
- Shin, C.S.; Liaw, S.K.; Yan, S.W. Post-Impact fatigue damage monitoring using Fiber Bragg Grating Sensors. Sensors 2014, 14, 4144–4153. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.M.; Kim, C.M.; Choi, S.Y.; Lee, B.Y. Enhanced strain measurement range of an FBG sensor embedded in seven-wire steel strands. Sensors 2017, 17, 1654. [Google Scholar] [CrossRef] [PubMed]






| Groove Shape | No Groove | U-Groove | U-Groove with Chamfer | Inverted Trapezoidal Groove | Trapezoidal Groove | V-Groove | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Specimen No. | 1–1 | 1–2 | 2–1 | 2–2 | 3–1 | 3–2 | 4–1 | 4–2 | 5–1 | 5–2 | 6–1 | 6–2 |
| Yield strength (kN) | 140 | 140 | 131 | 135 | 135 | 134 | 134 | 132 | 136 | 136 | 132 | 128 |
| Average yield strength (kN) | 140 | 133 | 134.5 | 133 | 136 | 130 | ||||||
| Reduction (%) | - | 5.00 | 3.93 | 5.00 | 2.85 | 7.14 | ||||||
| Peak strength (kN) | 215 | 212 | 199 | 206 | 205 | 204 | 203 | 204 | 205 | 204 | 204 | 200 |
| Average peak strength (kN) | 213.5 | 202.5 | 204.5 | 203.5 | 204.5 | 202 | ||||||
| Reduction (%) | - | 5.15 | 4.22 | 4.68 | 4.22 | 5.39 | ||||||
| Failure strength (kN) | 172 | 166 | 156 | 151 | 162 | 162 | 166 | 165 | 164 | 165 | 164 | 158 |
| Average failure strength (kN) | 166.5 | 153.5 | 162 | 162.5 | 165.5 | 161 | ||||||
| Reduction (%) | - | 7.81 | 2.70 | 0.60 | 0.60 | 3.30 | ||||||
| Groove Type | Maximum Stress Value (MPa) | Stress Concentration Factor |
|---|---|---|
| No-groove | 179 | - |
| U-groove | 359 | 2.01 |
| U-groove with chamfer | 348 | 1.94 |
| Inverted trapezoidal groove | 365 | 2.04 |
| Trapezoidal groove | 335 | 1.87 |
| V-groove | 378 | 2.11 |
| No. | Groove Shape | Glue Name | Main Component |
|---|---|---|---|
| 001 | Trapezoidal groove | Modified acrylate glue | Methacrylate and mix of some toughening agent, reinforcing agent, and stabilizer |
| 002 | Trapezoidal groove | 502 glue | Ethyl α-cyanoacrylate and mix of some toughening agent, reinforcing agent, and stabilizer |
| 003 | Trapezoidal groove | Epoxy resin A-B glue | Two components based on epoxy resin with high temperature resistance |
| 004 | Trapezoidal groove | H814-Epoxy resin glue | Epoxy resin, curing agent, methyl tetrahydrophthalic anhydride, aluminum hydroxide, and polyester poly |
| Part | Parameter |
|---|---|
| Optical channels | 4 individual channels |
| Wavelength range | 1525–1565 nm |
| Minimum wavelength spacing | 0.4 nm |
| Wavelength precision | ±1 pm |
| Scan and report rate | 500 Hz |
| Optical connector | Ferrule Connector/A-Physical Connection |
| Power supply | 220V AC 1A |
| Communication | USB 2.0 |
| Operating temperature | 0–40 °C |
| Dimensions | 480 × 400 × 95 mm |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Zhang, N.; Si, G.; Li, X. Study on the Optimal Groove Shape and Glue Material for Fiber Bragg Grating Measuring Bolts. Sensors 2018, 18, 1799. https://doi.org/10.3390/s18061799
Zhao Y, Zhang N, Si G, Li X. Study on the Optimal Groove Shape and Glue Material for Fiber Bragg Grating Measuring Bolts. Sensors. 2018; 18(6):1799. https://doi.org/10.3390/s18061799
Chicago/Turabian StyleZhao, Yiming, Nong Zhang, Guangyao Si, and Xuehua Li. 2018. "Study on the Optimal Groove Shape and Glue Material for Fiber Bragg Grating Measuring Bolts" Sensors 18, no. 6: 1799. https://doi.org/10.3390/s18061799
APA StyleZhao, Y., Zhang, N., Si, G., & Li, X. (2018). Study on the Optimal Groove Shape and Glue Material for Fiber Bragg Grating Measuring Bolts. Sensors, 18(6), 1799. https://doi.org/10.3390/s18061799






