Theoretical Analysis of a Microring Resonator Array with High Sensitivity and Large Dynamic Range Based on a Multi-Scale Technique
Abstract
:1. Introduction
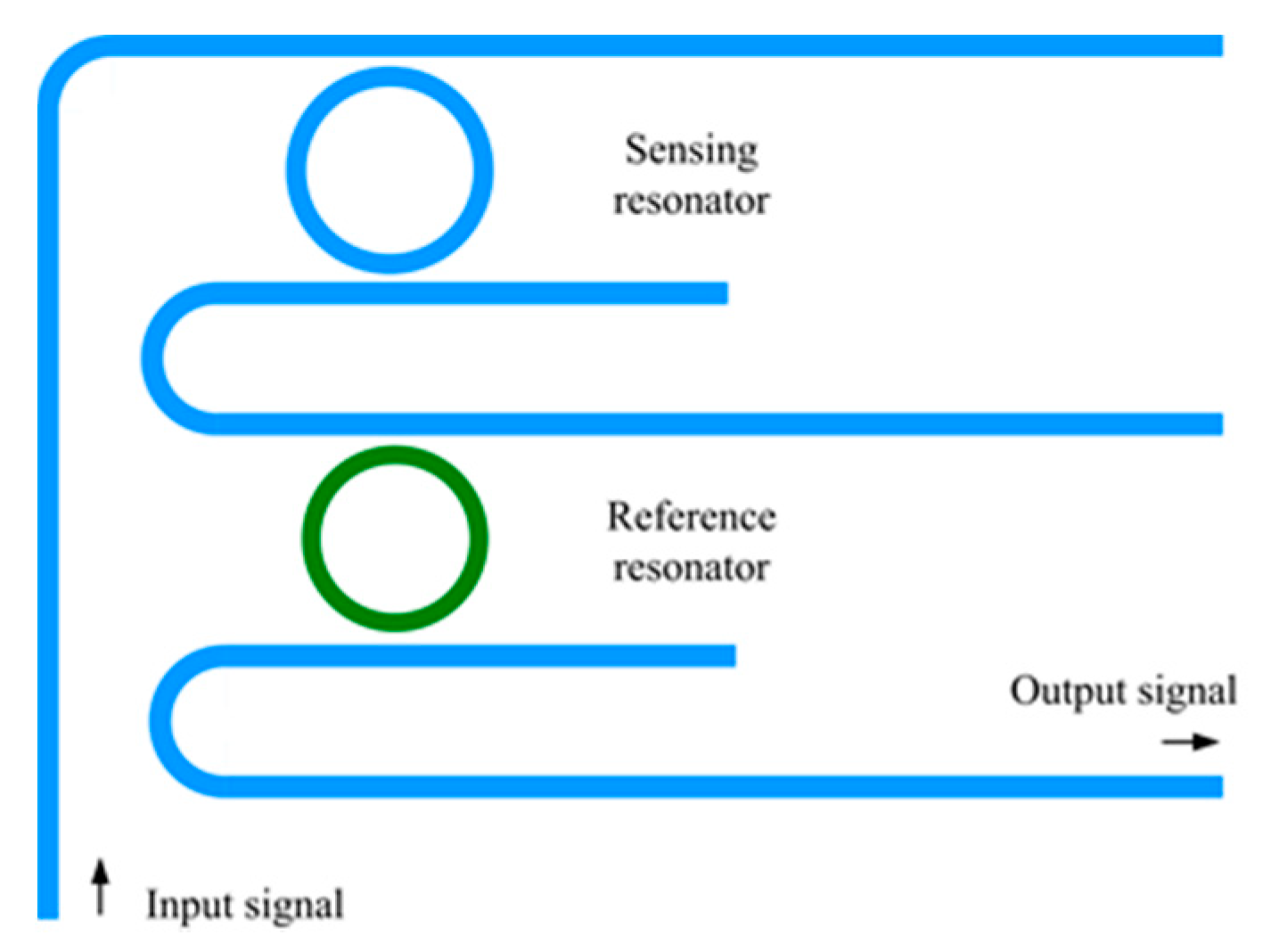
2. Sensor Design and Theoretical Analysis
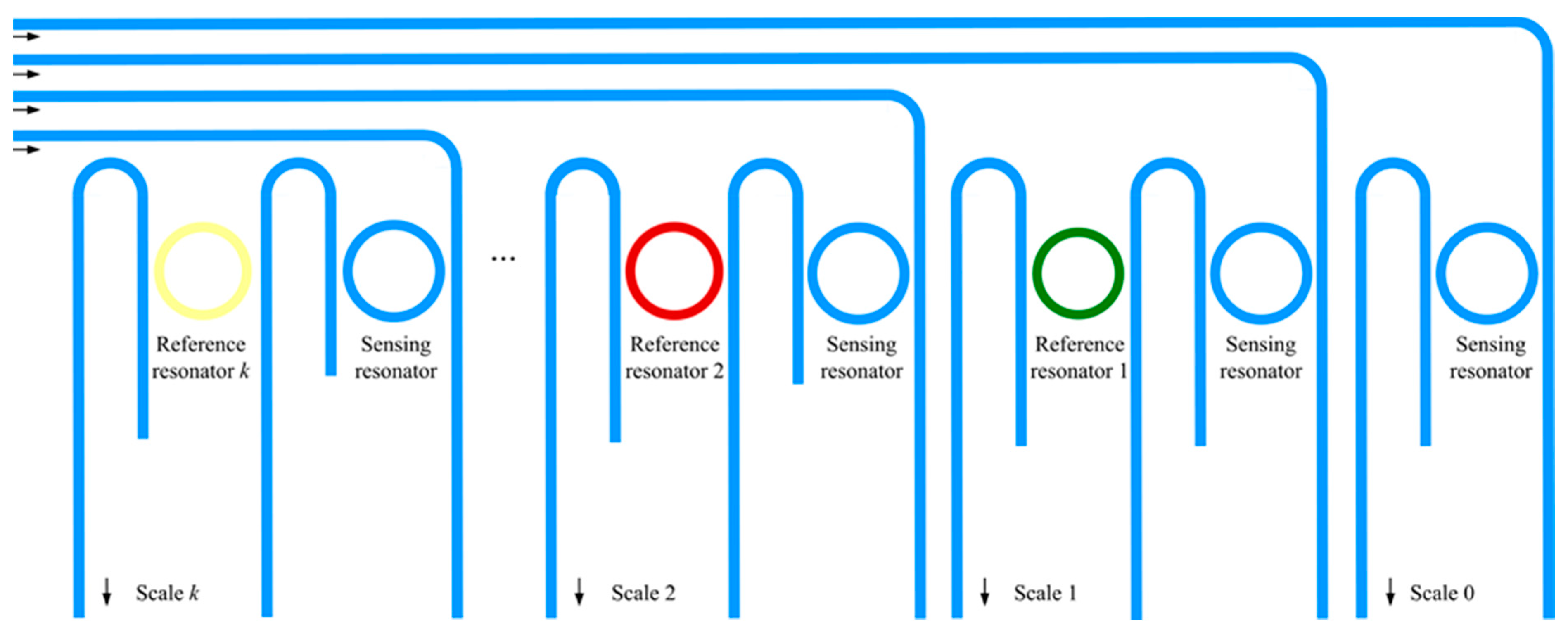
2.1. Multi-Scale Measurement Theory
2.2. Cascaded Microring Resonators and Sensitivity
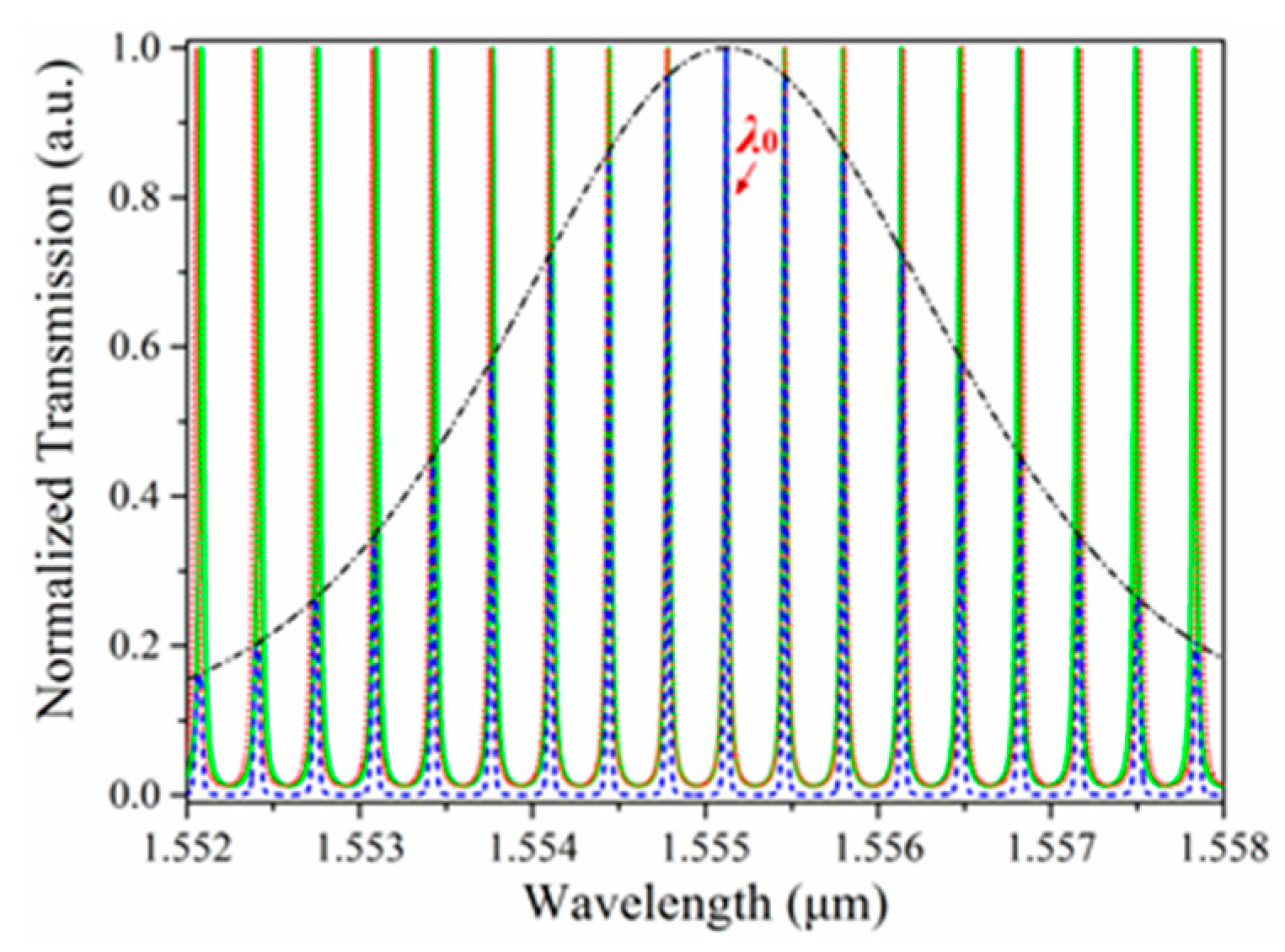
2.3. Detection Limit and Dynamic Range
3. Numerical Validations of Optical Transmissions
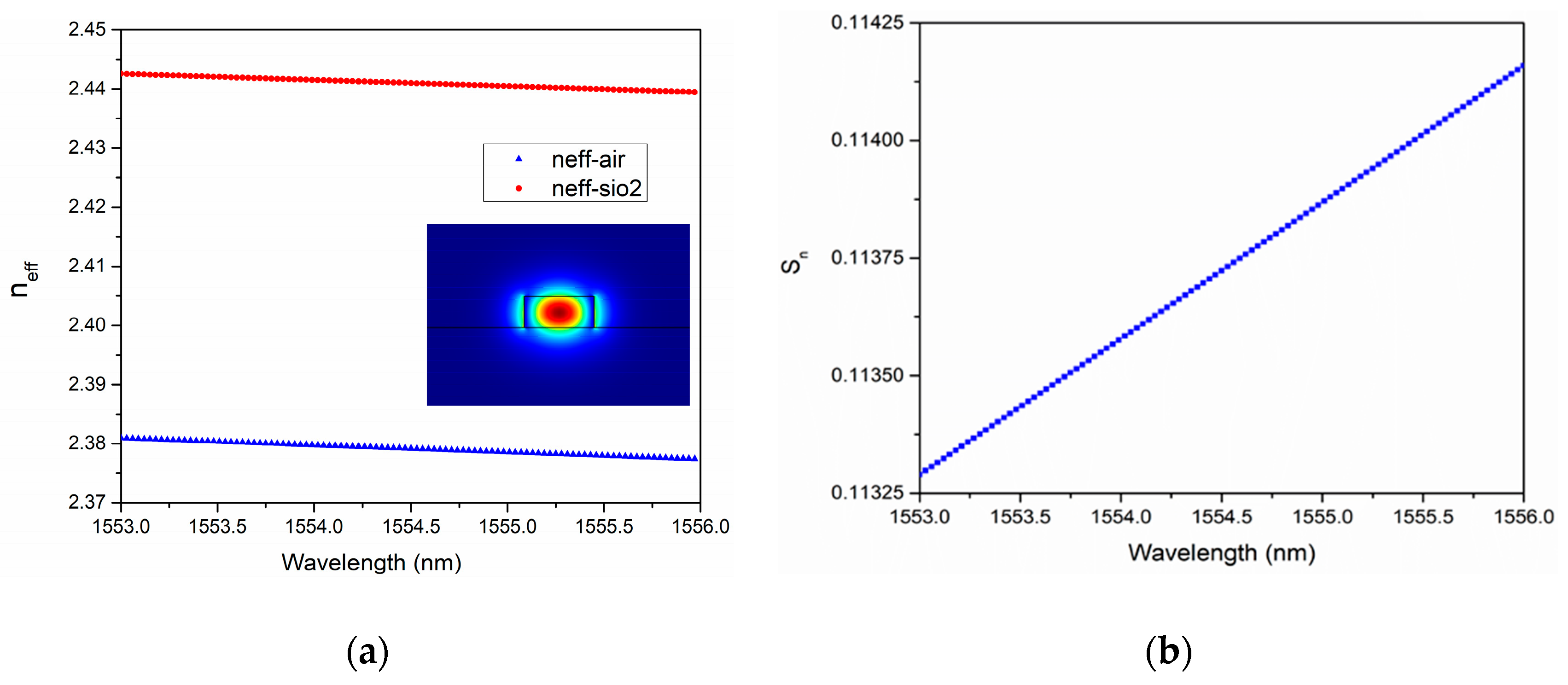
3.1. Simulation Setting
3.2. Simulation Results
4. Conclusion
Author Contributions
Funding
Conflicts of Interest
References
- Malka, D.; Cohen, M.; Turkiewicz, J.; Zalevsky, Z. Optical micro-multi-racetrack resonator filter based on SOI waveguides. Photonics Nanostruct. Fundam. Appl. 2015, 16, 16–23. [Google Scholar] [CrossRef]
- De Vos, K.; Bartolozzi, I.; Schacht, E.; Bienstman, P.; Baets, R. Silicon-on-Insulator microring resonator for sensitive and label-free biosensing. Opt. Express 2007, 15, 7610–7615. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Ye, J.; Zou, J.; Li, M.; He, J. Cascaded silicon-on-insulator double-ring sensors operating in high-sensitivity transverse-magnetic mode. Opt. Lett. 2013, 38, 1349–1351. [Google Scholar] [CrossRef] [PubMed]
- Kindt, J.T.; Bailey, R.C. Biomolecular analysis with microring resonators: Applications in multiplexed diagnostics and interaction screening. Curr. Opin. Chem. Biol. 2013, 17, 818–826. [Google Scholar] [CrossRef] [PubMed]
- Park, M.K.; Kee, S.J.; Quah, Y.J.; Netto, V.; Song, J.; Fang, Q.; Fosse, E.M.L.; Lo, G. Label-free aptamer sensor based on silicon microring resonators. Sens. Actuators B Chem. 2013, 176, 552–559. [Google Scholar] [CrossRef]
- Pattnaik, P.K.; Vijayaaditya, B.; Srinivas, T.; Selvarajan, A. Optical MEMS pressure and vibration sensors using integrated optical ring resonators. In Proceedings of the 4th IEEE Sensors Conference, Irvine, CA, USA, 30 October–2 November 2005; pp. 636–639. [Google Scholar]
- Zhao, X.; Tsai, J.M.; Cai, H.; Ji, M.; Zhou, J.; Bao, M.H.; Huang, Y.P.; Kwong, D.L.; Liu, A.Q. A nano-opto-mechanical pressure sensor via ring resonator. Opt. Express 2012, 20, 8535–8542. [Google Scholar] [CrossRef] [PubMed]
- Kolli, V.R.; Srinivasulu, T.; Hegde, G.; Badrinarayana, T.; Talabattula, S. Design and analysis of serially coupled double microring resonator based force sensor for 1 μN range measurement. Optik-Int. J. Light Electron. Opt. 2017, 131, 1063–1070. [Google Scholar] [CrossRef]
- Bhola, B.; Steier, W.H. A Novel Optical Microring Resonator Accelerometer. IEEE Sens. J. 2007, 7, 1759–1766. [Google Scholar] [CrossRef]
- Mo, W.; Zhou, Z.; Wu, H.; Gao, D. Silicon-Based stress-coupled optical racetrack resonators for seismic prospecting. IEEE Sens. J. 2011, 11, 1035–1039. [Google Scholar] [CrossRef]
- Katz, O.; Malka, D. Design of novel SOI 1 × 4 optical power splitter using seven horizontally slotted waveguides. Photonics Nanostruct. Fundam. Appl. 2017, 25, 9–13. [Google Scholar] [CrossRef]
- Nikolaevsky, L.; Shchori, T.; Malka, D. Modeling a 1 × 8 MMI Green Light Power Splitter Based on Gallium-Nitride Slot Waveguide Structure. Photonics Tech. Lett. 2018, 30, 720–723. [Google Scholar] [CrossRef]
- Dai, D. Highly sensitive digital optical sensor based on cascaded high-Q ring-resonators. Opt. Express 2009, 17, 23817–23822. [Google Scholar] [CrossRef] [PubMed]
- Nott, M.L.; Passaro, V.M.N. Ultra high sensitivity chemical photonic sensing by Mach-Zehnder interferometer enhanced Vernier-effect. Sens. Actuators B Chem. 2013, 176, 994–1007. [Google Scholar] [CrossRef]
- Yan, H.; Huang, L.; Xu, X.; Chakravarty, S.; Tang, N.; Tian, H.; Chen, R.T. Unique surface sensing property and enhanced sensitivity in microring resonator biosensors based on subwavelength grating waveguides. Opt. Express 2016, 24, 29724–29733. [Google Scholar] [CrossRef] [PubMed]
- Claes, T.; Bogaerts, W.; Bienstman, P. Experimental characterization of a silicon photonic biosensor consisting of two cascaded ring resonators based on the Vernier-effect and introduction of a curve fitting method for an improved detection limit. Opt. Express 2010, 18, 22747–22761. [Google Scholar] [CrossRef] [PubMed]
- Zamora, V.; Lützow, P.; Weiland, M.; Pergande, D. A Highly sensitive refractometric sensor based on cascaded SiN microring resonators. Sensors 2013, 13, 14601–14610. [Google Scholar] [CrossRef] [PubMed]
- Jin, L.; Li, M.; He, J.J. Highly-sensitive silicon-on-insulator sensor based on two cascade micro-ring resonators with vernier effect. Opt. Commun. 2011, 284, 156–159. [Google Scholar] [CrossRef]
- Notte, M.L.; Troia, B.; Muciaccia, T.; Campanella, C.E.; Leonardis, F.D.; Passaro, V.M.N. Recent advances in gas and chemical detection by Vernier effect-based photonic sensors. Sensors 2014, 14, 4831–4855. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Zhang, X.; Lu, L.; Chen, J. Tunable Vernier Microring Optical Filters with P-I-P Type Microheaters. IEEE Photonics J. 2013, 5, 6601211. [Google Scholar] [CrossRef]
- Boeck, R.; Shi, W.; Chrostowski, L.; Jaeger, N.A.F. FSR-eliminated Vernier racetrack resonators using grating-assisted couplers. IEEE Photonics J. 2013, 5, 2202511. [Google Scholar] [CrossRef]
- Eisele, A. Millimeter-Precision Laser Rangefinder Using A Low-Cost Photon Counter; KIT Scientific Publishing: Karlsruhe, Germany, 2014; pp. 19–20. [Google Scholar]
- White, I.M.; Fan, X. On the performance quantification of resonant refractive index sensors. Opt. Express 2008, 16, 1020–1028. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Yuan, J.; Ma, T.; Sang, X.; Yan, B.; Wang, K.; Yu, C. Design and optimization of silicon concentric dual-microring resonators for refractive index sensing. Opt. Commun. 2017, 395, 212–216. [Google Scholar] [CrossRef]



| Parameter | Symbol | Value |
|---|---|---|
| Core width | Wcore | 0.5 μm |
| Core height | Hcore | 0.22 μm |
| Refractive index of core (Si) | n1 | 3.476 |
| Refractive index of upper and bottom cladding (SiO2) | n2 | 1.445 |
| Refractive index of upper cladding (Air) | nair | 1.0 |
| Free spectral range (FSR) of Sensing Resonator | FSRsen | 18.01 pm |
| FSR of Reference Resonator 1 | FSRref,1 | 20.01 pm |
| FSR of Reference Resonator 2 | FSRref,2 | 18.19 pm |
| Type | Initial Wavelength (nm) | Resonant Wavelength Shift (pm) | Sensitivity (nm/RIU) | Dynamic Range Improvement (dB) |
|---|---|---|---|---|
| Scale 0 | 1554.9868 | 17.75 | 44.37 | - |
| Scale 1 | 1554.9866 | 18.01 | 450.23 | 10.06 |
| Scale 2 | 1554.9144 | 18.20 | 4550 | 20.11 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mo, W.; Liu, H.; Jin, F.; Song, J.; Dong, K. Theoretical Analysis of a Microring Resonator Array with High Sensitivity and Large Dynamic Range Based on a Multi-Scale Technique. Sensors 2018, 18, 1987. https://doi.org/10.3390/s18071987
Mo W, Liu H, Jin F, Song J, Dong K. Theoretical Analysis of a Microring Resonator Array with High Sensitivity and Large Dynamic Range Based on a Multi-Scale Technique. Sensors. 2018; 18(7):1987. https://doi.org/10.3390/s18071987
Chicago/Turabian StyleMo, Wenqin, Huiyun Liu, Fang Jin, Junlei Song, and Kaifeng Dong. 2018. "Theoretical Analysis of a Microring Resonator Array with High Sensitivity and Large Dynamic Range Based on a Multi-Scale Technique" Sensors 18, no. 7: 1987. https://doi.org/10.3390/s18071987





