Design and Modeling of a Test Bench for Dual-Motor Electric Drive Tracked Vehicles Based on a Dynamic Load Emulation Method
Abstract
:1. Introduction
2. Structure of a DDTV
3. Analysis of DDTV Dynamics
3.1. Longitudinal Dynamics Analysis
3.2. Calculation of Equivalent Rotational Inertia
4. Modelling the Test Bench System
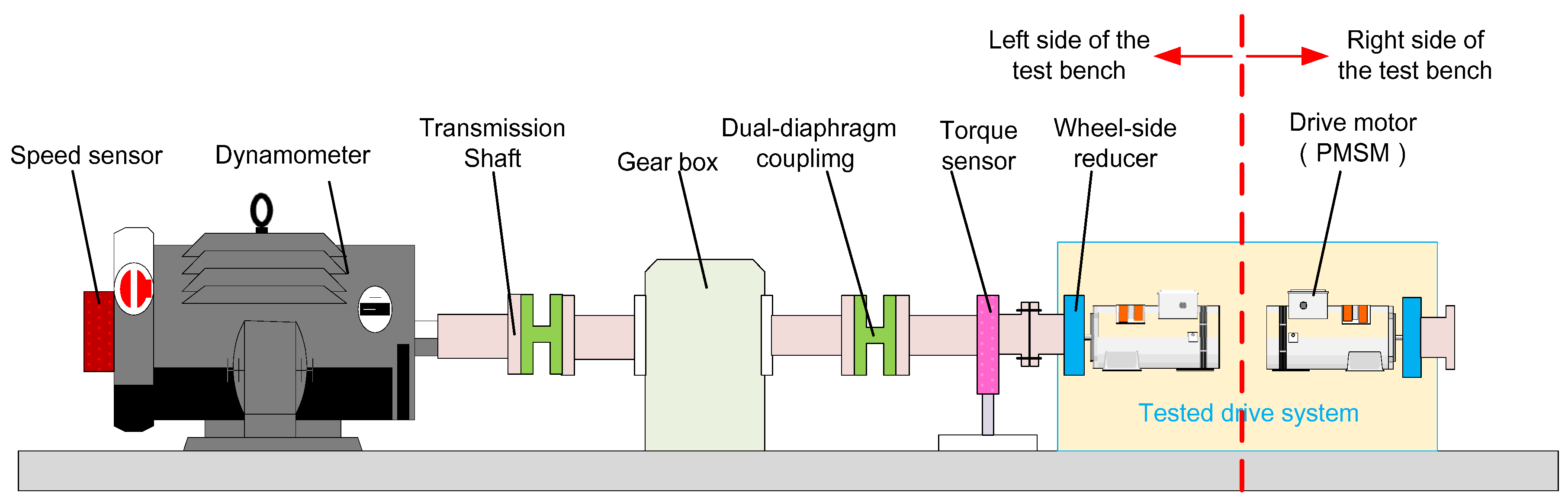
4.1. Design of the Test Bench
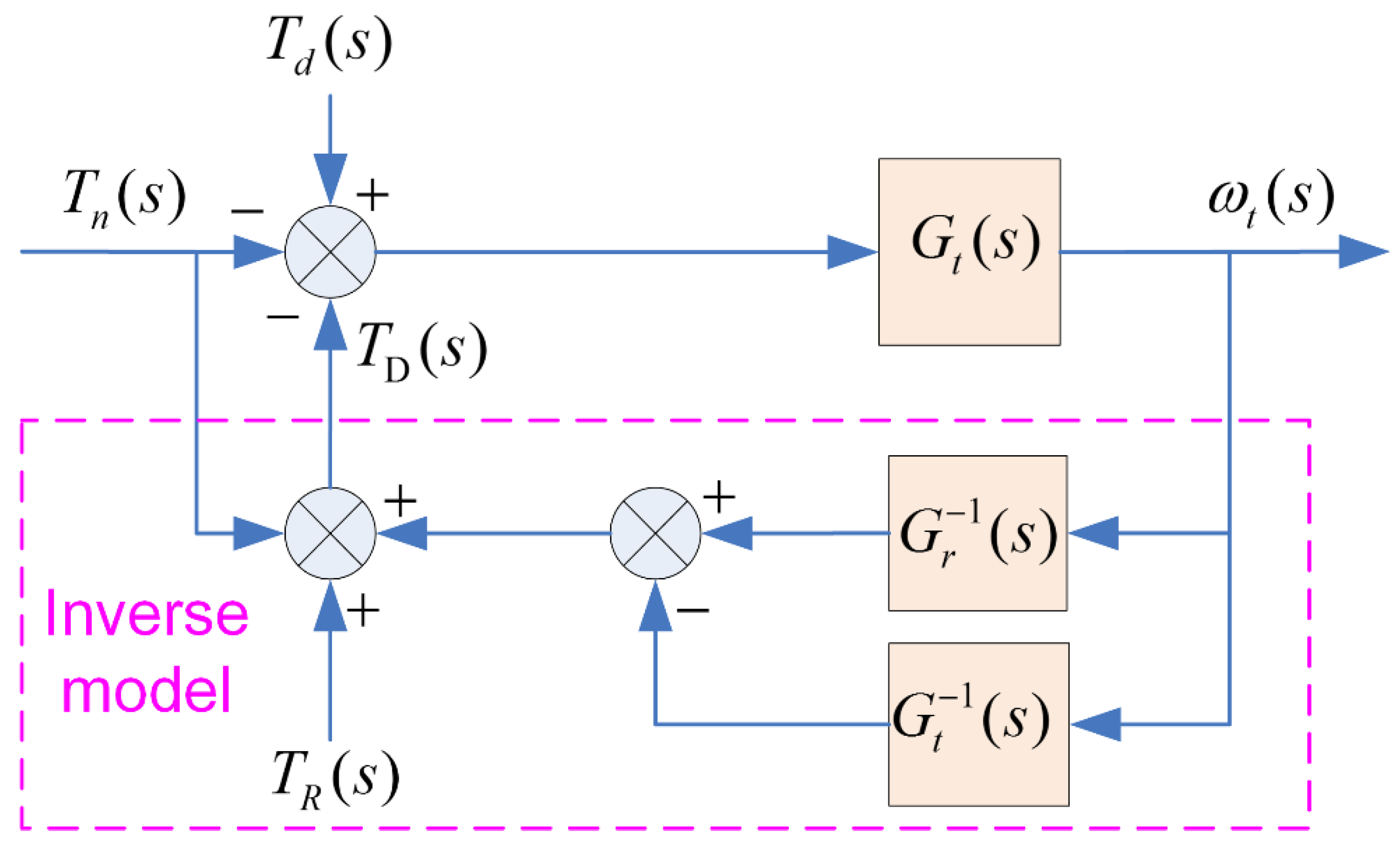
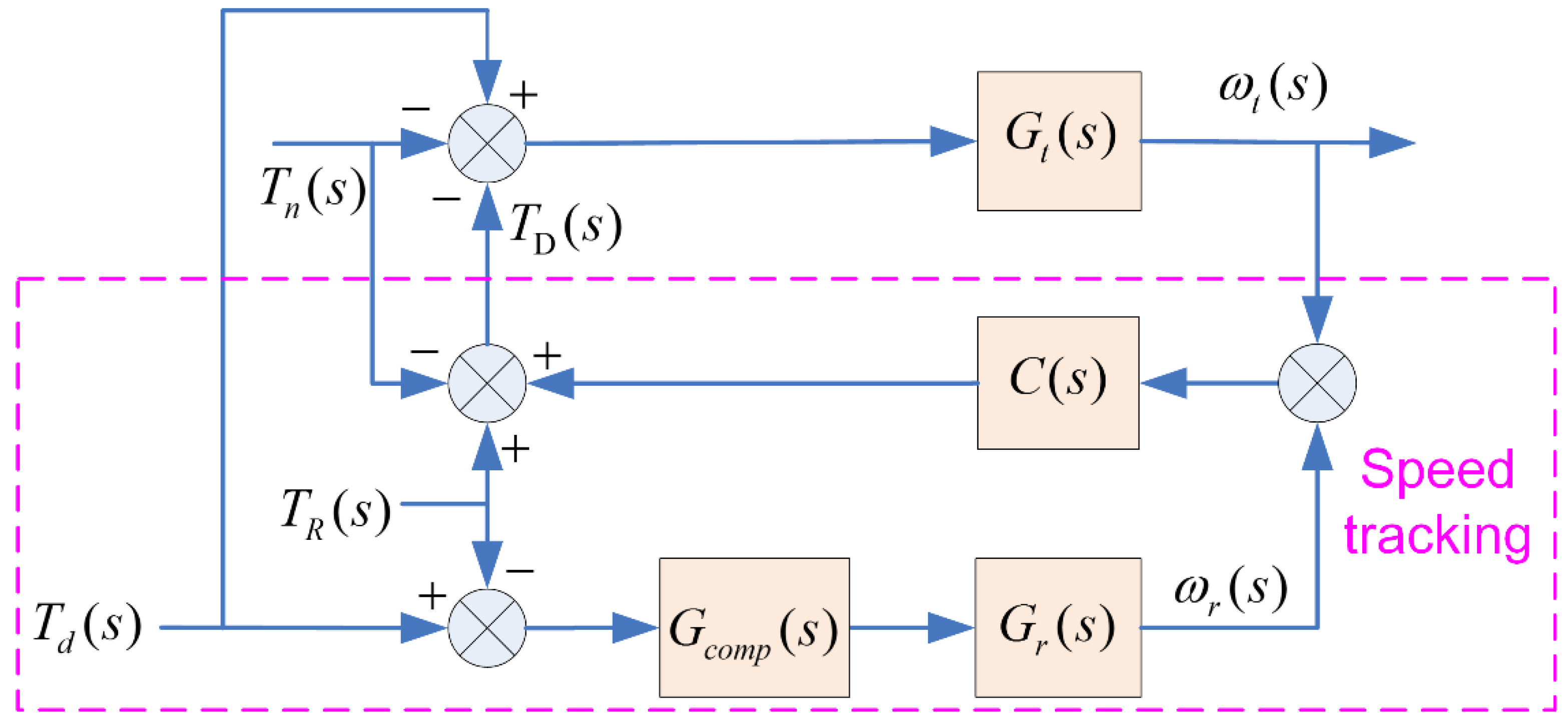
4.2. Speed Tracking Method
- (1)
- On one hand, when a DDTV straightly runs on a real road, the transfer function model of the vehicle is shown in Figure 4a, and can be described as:where, is the speed of drive wheel on a real road in rad/s, here we call it reference speed. is the drive torque of a single side drive wheel, is the resistance torque acting on a single side drive wheel.
- (2)
- On the other hand, when a DDTV is tested on a bench, the transfer function model of the vehicle is shown in Figure 4b, and can be described as:where, is the actual speed of drive wheel on the test bench in rad/s, here we call it actual speed. is the load torque imposed by the dynamometer, is the frictional resistance torque of the platform transmission system, mainly consists of bearing viscous friction, sliding friction caused by gear teeth meshing and wind friction.
4.3. System Modeling
4.3.1. Vehicle Drive System
4.3.2. Load Emulation System
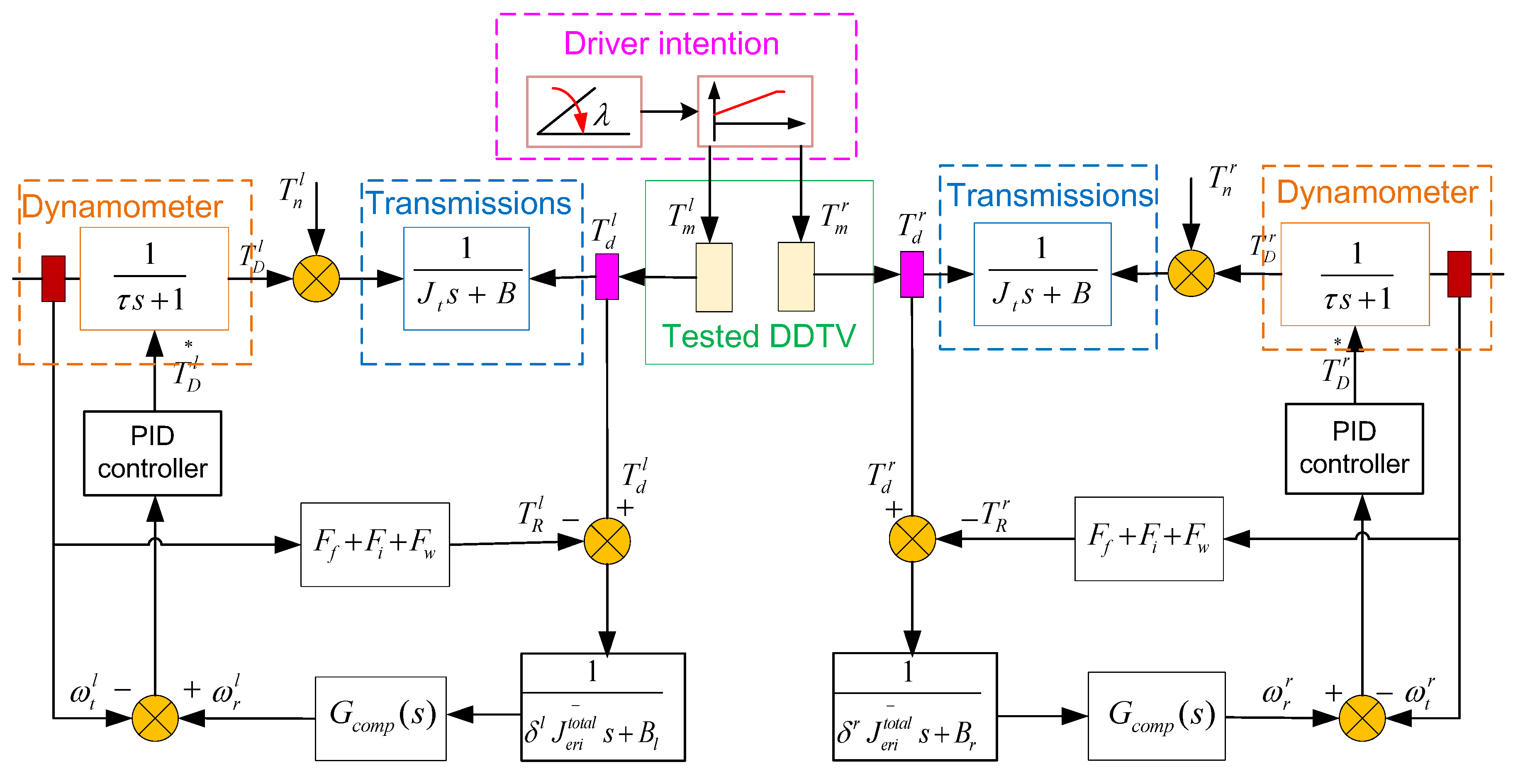
4.4. Control Strategy and Simulink Model
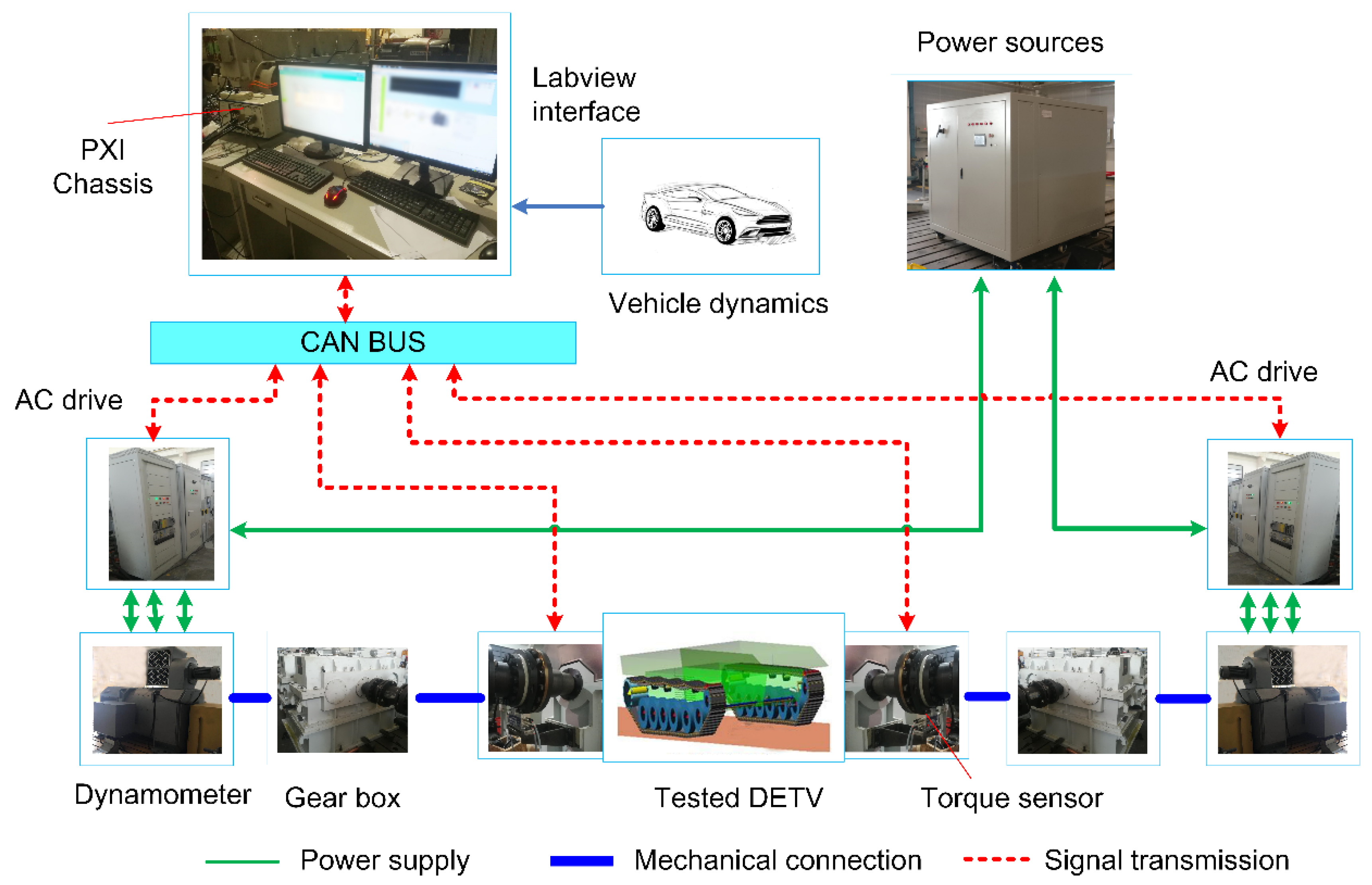
5. Experiment System Introduction.
5.1. General Setup
5.2. Device Parameters
5.3. Test Contents
6. Results and Discussion
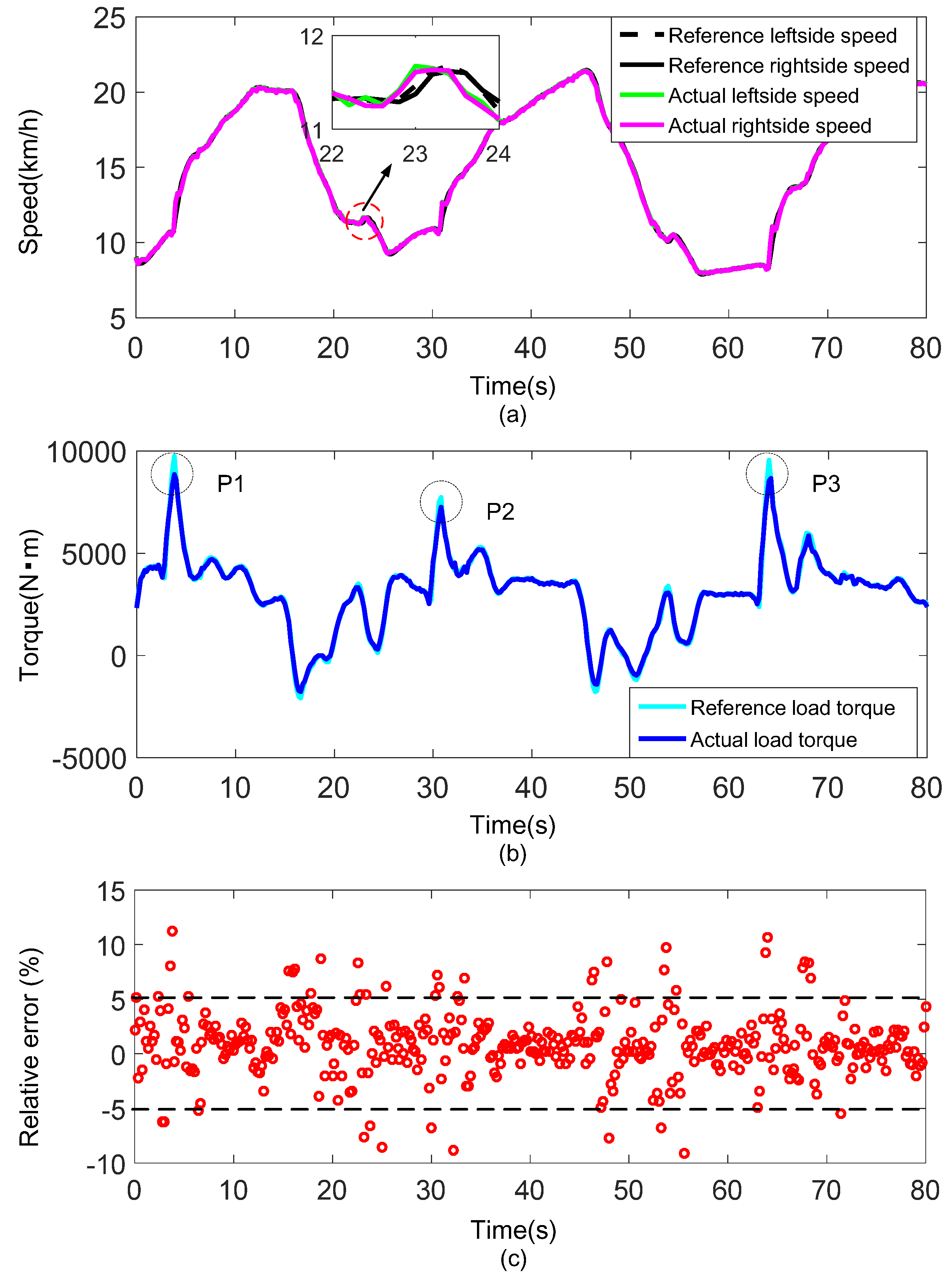
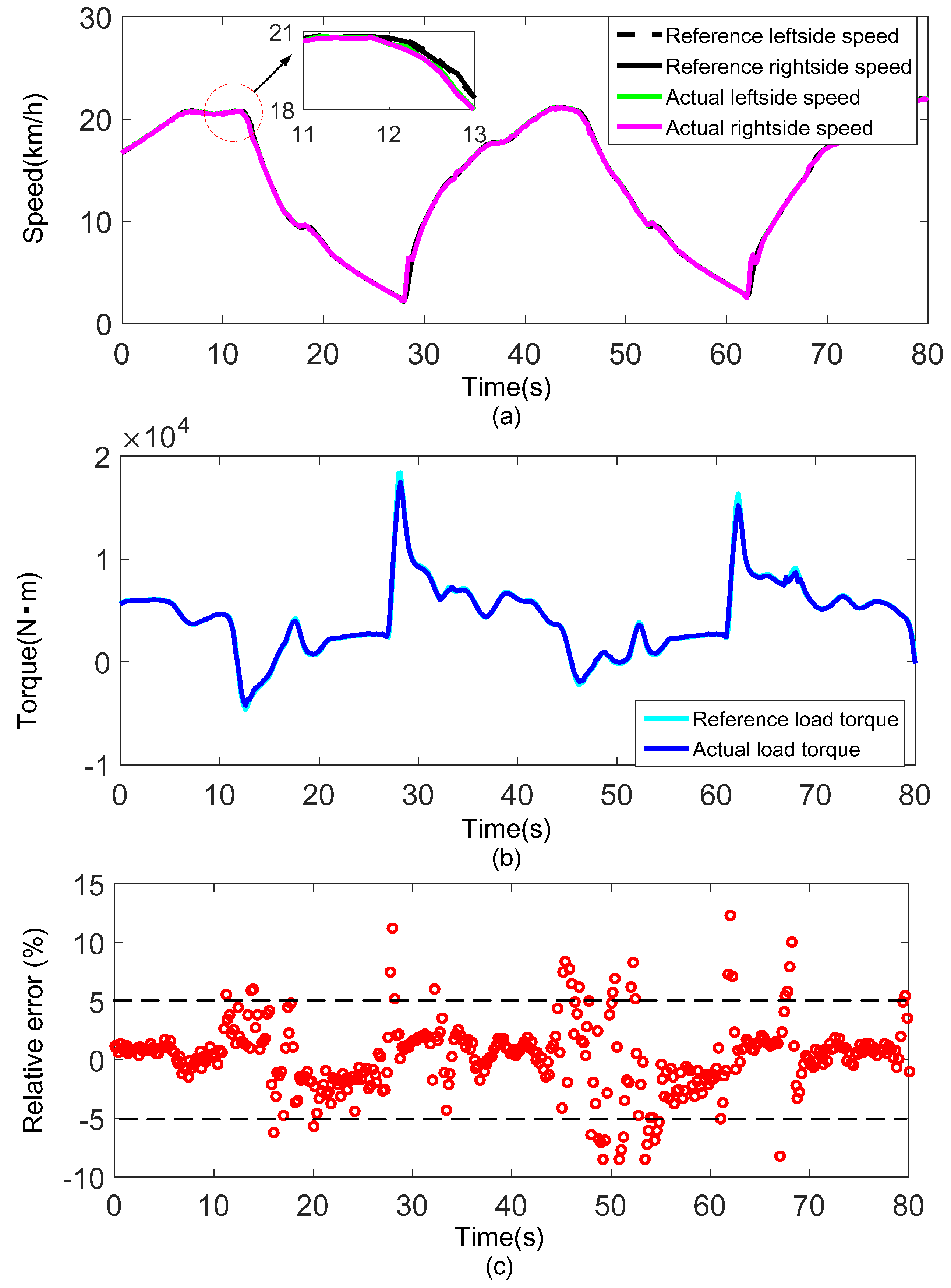
6.1. Effectiveness Validation of the Dynamic Load Emulation Method
6.1.1. Straight Line with Different Vehicle Masses
6.1.2. Straight Line with Slopes
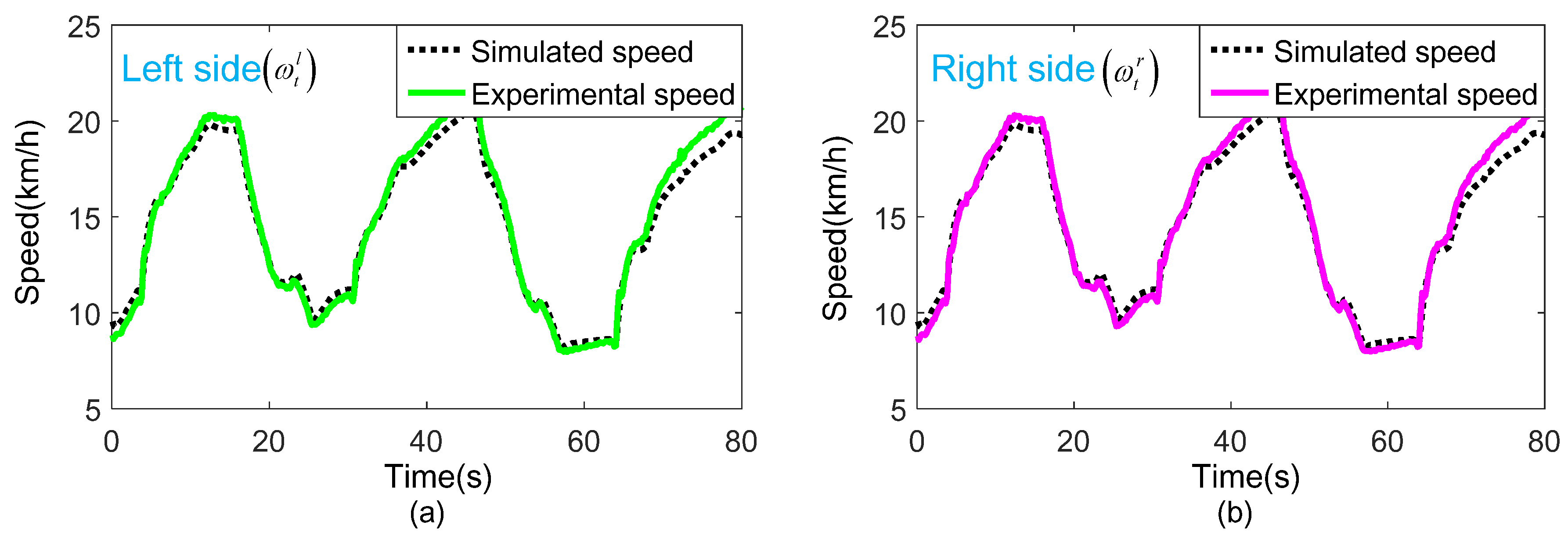
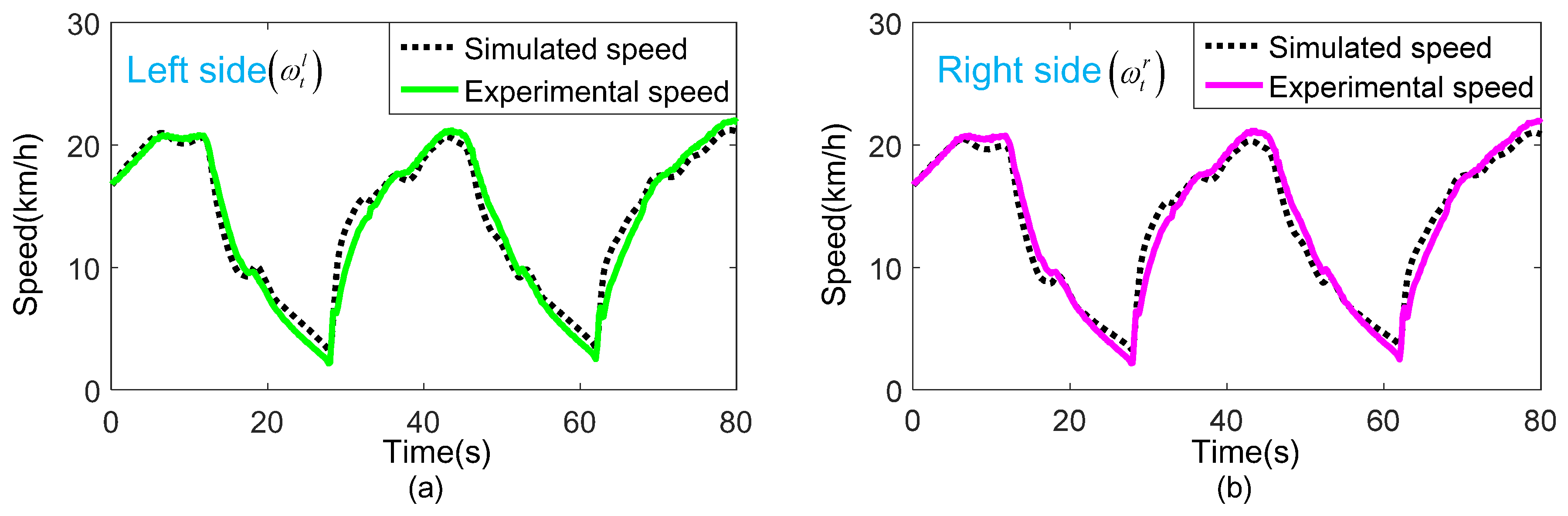
6.2. Accuracy Validation of the Test. Bench Simulation Model.
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zou, Y.; Zhang, C.N.; Sun, F.C.; Wu, J.B. Dynamic Control of Dual-Motor Drive Tracked Vehicles. Trans. Beijing Inst. Technol. 2007, 27, 956–960. [Google Scholar]
- Gai, J.T.; Huang, S.D.; Zhou, G.M.; Liu, Y.; Ma, T. Adaptive Sliding Mode Steering Control of Double Motor Coupling Drive Transmission for Tracked Vehicle. Acta Armamentarii 2015, 36, 405–411. [Google Scholar] [CrossRef]
- Ma, X.J.; Su, J.Q.; Wei, S.G.; Liu, Q.L.; Xiang, Y. Torque Compensate Control of Dual-motor Electric Drive Armored Vehicle. Acta Armamentarii 2013, 11, 1373–1379. [Google Scholar] [CrossRef]
- Zhai, L.; Huang, H.; Kavuma, S. Investigation on a Power Coupling Steering System for Dual-Motor Drive Tracked Vehicles Based on Speed Control. Energies 2017, 10, 1118. [Google Scholar] [CrossRef]
- Wang, H.; Song, Q.; Wang, S.B.; Zeng, P. Dynamic Modeling and Control Strategy Optimization for a Hybrid Electric Tracked Vehicle. Math. Probl. Eng. 2015, 2015, 251906. [Google Scholar] [CrossRef]
- Zou, Y.; Sun, F.; Hu, X.S.; Guzzella, L.; Peng, H. Combined Optimal Sizing and Control for a Hybrid Tracked Vehicle. Energies 2012, 5, 4697–4710. [Google Scholar] [CrossRef] [Green Version]
- Zou, Y.; Liu, T.; Liu, D.X.; Sun, F.C. Reinforcement learning-based real-time energy management for a hybrid tracked vehicle. Appl. Energy 2016, 171, 372–382. [Google Scholar] [CrossRef]
- Wang, H.; Huang, Y.J.; Khajepour, A.; Song, Q. Model predictive control-based energy management strategy for a series hybrid electric tracked vehicle. Appl. Energy 2016, 182, 105–114. [Google Scholar] [CrossRef]
- Liu, T.; Hu, X.S. A Bi-Level Control for Energy Efficiency Improvement of a Hybrid Tracked Vehicle. IEEE Trans. Ind. Inf. 2018, 99, 1616–1625. [Google Scholar] [CrossRef]
- Wang, H.Y.; Wang, Q.L.; Rui, Q.; Gai, J.T.; Zhou, G.M. Analyzing and Testing Verification the Performance about High-speed Tracked Vehicles in Steering Process. Chin. J. Mech. 2014, 50, 162–172. [Google Scholar] [CrossRef]
- Wipke, K.B.; Cuddy, M.R.; Burch, S.D. ADVISOR 2.1: A user-friendly advanced powertrain simulation using a combined backward/forward approach. IEEE Trans. Veh. Technol. 1999, 48, 1751–1761. [Google Scholar] [CrossRef]
- Wang, Q.N.; Yu, Y.T.; Zeng, X.H.; Yu, Y.B. Development of forward-looking simulation platform for hybrid electric vehicle based on software CRUISE. J. Jilin Univ. 2009, 39, 1413–1419. [Google Scholar]
- Ma, X.G.; Yang, T.; You, X.M.; Zhai, B. Modeling and Simulation of Multibody Dynamics for Tracked Vehicle Based on Recurdyn. In Proceedings of the International IEEE Conference on Intelligent Networks and Intelligent Systems, Shenyang, China, 1–3 November 2010; pp. 669–671. [Google Scholar]
- Bartlett, W.D. Calculation of deceleration rates for S-Cam Air-Braked heavy trucks equipped with Anti-Lock brake systems. SAE Tech. Pap. 2007. [Google Scholar] [CrossRef]
- Fajri, P.; Prabhala, V.A.K.; Ferdowsi, M. Emulating On-Road Operating Conditions for Electric-Drive Propulsion Systems. IEEE Trans. Energy Convers. 2016, 31, 1–11. [Google Scholar] [CrossRef]
- Li, W.; Zhang, C.N.; Song, Q. Dual-test bench for high-power traction motor propulsion system on EV. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Harbin, China, 3–5 September 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Schupbach, R.M.; Balda, J.C. A versatile laboratory test bench for developing powertrains of electric vehicles. In Proceedings of the Vehicular Technology Conference, Vancouver, BC, Canada, 24–28 September 2002; pp. 1666–1670. [Google Scholar] [CrossRef]
- Bendjedia, M.; Berthon, A.; Gustin, F. Test bench for converters reliability studies for EV and HEV electrical vehicle applications. In Proceedings of the IEEE European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–13. [Google Scholar]
- He, H.W.; Sun, F.C.; Xing, J. Dynamic simulation and experiment of electric drive system on test bench. In Proceedings of the IEEE International Conference on Vehicular Electronics and Safety, Beijing, China, 13–15 December 2007; pp. 1–4. [Google Scholar] [CrossRef]
- Wang, J.; Yang, K.; Wang, J. Design of a test bench for new energy vehicle power motor systems. Chin. J. Automot. Eng. 2017, 7, 407–414. [Google Scholar]
- Yang, J.J.; Zhou, X.J.; Wei, Y.D.; Gong, Y. Test bed modeling and control method for track vehicle. Trans. Chin. Soc. Agric. Mach. 2013, 44, 8–13. [Google Scholar] [CrossRef]
- Cheng, G.W.; Zhou, Z.L.; Xu, L.Y.; Deng, C.N.; Zhang, Y.J. Simulation of the Driving Load of Tracked Vehicle on Power Train Test Bench. Tract. Farm Transp. 2006, 4, 12–14. [Google Scholar]
- Chen, Q.Q.; Wu, X.Q.; Sun, T.L.; Liu, T.T. Research on New Automotive Drum Bench and Control System. Appl. Mech. Mater. 2014, 602, 1459–1462. [Google Scholar] [CrossRef]
- Collins, E.R.; Huang, Y. A programmable dynamometer for testing rotating machinery using a three-phase induction machine. IEEE Trans. Energy Convers. 1994, 9, 521–527. [Google Scholar] [CrossRef]
- Kyslan, K.; Ďurovský, F. Dynamic Emulation of Mechanical Loads-An Approach Based on Industrial Drives’ Features. Automatika 2013, 54, 356–363. [Google Scholar] [CrossRef]
- Song, Q.; Sun, F.C.; Zhen, M.Q. Inertia Matching during Dynamic Simulation of Vehicle Drive System on Test Bench. Trans. Beijing Inst. Technol. Ed. 2004, 2, 197–201. [Google Scholar]
- Gong, W.B.; Liu, A.L.; Jiang, K. Research on the technique of mechanical inertia mix electric simulation. Trans. Chin. Soc. Agric. Mach. 2009, 40, 208–212. [Google Scholar]
- Zhang, W.G.; Zhou, N.N. The Electric Simulation for Mechanical Inertia in Vehicle Bedstead Test System. Automot. Eng. 1998, 20, 312–316. [Google Scholar]
- Wang, W.J.; Zhang, W.G.; Li, X. Inertia electrical emulation and angular acceleration estimation for transmission test rig. J. Southeast Univ. Nat. Sci. Ed. 2012, 42, 62–66. [Google Scholar] [CrossRef]
- Sandholdt, P.; Ritchie, E.; Pedersen, J.K.; Betz, R.E. A dynamometer performing dynamic emulation of loads with non-linear friction. In Proceedings of the IEEE International Symposium on Industrial Electronics, Warsaw, Poland, 17 June 1996; pp. 873–878. [Google Scholar] [CrossRef]
- Gan, C.; Todd, R.; Apsley, J.M. Drive System Dynamics Compensator for a Mechanical System Emulator. IEEE Trans. Ind. Electron. 2015, 62, 70–78. [Google Scholar] [CrossRef]
- Kyslan, K.; Rodic, M.; Ľuboš, S. Industrial controller-based dynamometer with dynamic emulation of mechanical loads. Electr. Eng. 2017, 3, 1–10. [Google Scholar] [CrossRef]
- Rodic, M.; Jezernik, K.; Trlep, M. Dynamic emulation of mechanical loads: An advanced approach. IEE Proc. Electr. Power Appl. 2006, 153, 159–166. [Google Scholar] [CrossRef]
- Rodic, M.; Jezernik, K.; Trlep, M. Control Design in Mechatronic Systems Using Dynamic Emulation of Mechanical Loads. In Proceedings of the IEEE International Symposium on Industrial Electronics, Dubrovnik, Croatia, 20–23 June 2005; pp. 1635–1640. [Google Scholar] [CrossRef]
- Arellano-Padilla, J.; Asher, G.M.; Sumner, M. Control of an AC Dynamometer for Dynamic Emulation of Mechanical Loads with Stiff and Flexible Shafts. IEEE Trans. Ind. Electron. 2006, 53, 1250–1260. [Google Scholar] [CrossRef]
- Akpolat, Z.H.; Asher, G.M.; Clare, J.C. Dynamic emulation of mechanical loads using a vector-controlled induction motor-generator set. IEEE Trans. Ind. Electron. 1999, 46, 370–379. [Google Scholar] [CrossRef]
- Guzzella, L.; Sciarretta, A. Vehicle Propulsion Systems: Introduction to Modeling and Optimization; Springer: Berlin, Germany, 2005; pp. 67–162. ISBN 978-3-642-09415-6. [Google Scholar]
- Ye, X.; Jin, Z.H.; Gao, D.W.; Lu, Q.C. Dynamometer controller algorithm for road load emulations. J. Tsinghua Univ. 2013, 53, 1492–1497. [Google Scholar] [CrossRef]
- Kyslan, K.; Kušnír, E.; Fedák, V. Dynamic emulation of mechanical loads with backlash based on rapid control prototyping. In Proceedings of the IEEE Power Electronics and Motion Control Conference and Exposition, Antalya, Turkey, 21–24 September 2014; pp. 1209–1215. [Google Scholar] [CrossRef]
- Li, W.L.; Shi, X.H.; Ke, J.; Guo, D.; Yi, P. Dynamic simulation technology for powertrain test bench. Chin. J. Highw. Transp. 2014, 27, 120–126. [Google Scholar]
- Akpolat, Z.H.; Asher, G.M.; Clare, J.C. Experimental dynamometer emulation of nonlinear mechanical loads. IEEE Trans. Ind. Appl. 1999, 35, 1367–1373. [Google Scholar] [CrossRef]
- Qiang, R.; Wang, H.Y.; Wang, Q.L. Research on the Acquisition of Steering Performance Parameters of Armored Vehicle Based on Experiments. Chin. J. Mech. 2015, 51, 127–136. [Google Scholar] [CrossRef]
- Tang, S.; Yuan, S.; Hu, J. Modeling of steady-state performance of skid-steering for high-speed tracked vehicles. J. Terramech. 2017, 73, 25–35. [Google Scholar] [CrossRef]






| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Vehicle mass, m(t) | 20, 30 | Approach angle, | 28.30 |
| Drive wheel radius, R(m) | 0.286 | Departure angle, | 30.10 |
| Frontal area of the vehicle, A(m2) | 4.84 | Ratio of the wheel-side reducer, iwr | 30 |
| Aerodynamic drag, CD | 1 | Rolling resistance coefficient, f | 0.05 |
| Air density, ρ(Ns2/m4) | 1.22 | Rotational inertia of the dynamometer, JD (kg·m2) | 42.60 |
| Rotational inertia of the gear box, Jgb (kg·m2) | 491.10 | Damping coefficient of the load emulation system, B(Nms/rad) | 27 |
| Total rotational inertia of the shaft attachments, Jc(kg·m2) | 7.95 | Time constant of the dynamometer, T(s) | 0.001 |
| Maximum power of the test bench (kw) | 2400 | Sampling time the algorithm for dynamic load emulation (Hz) | 500 |
| Group | Mass of the DDTV | Driving conditions |
|---|---|---|
| 1 | m = 20 t | Straight line without slope, θ = 0° |
| 2 | m = 30 t | Straight line without slope, θ = 0° |
| 3 | m = 30 t | Straight line with slope, θ = 4°, 8°, 12°, 15°, 18°, 20° |
| Slope Angles | ||||||
|---|---|---|---|---|---|---|
| 4° | 8° | 12° | 15° | 18° | 20° | |
| Time range (s) | 3–4 | 20–21 | 48–49 | 71–72 | 85–86 | 97–98 |
| Reference load torque (N·m) | 10,173.59 | 16,163.96 | 21,587.55 | 25,693.44 | 30,045.67 | 33,130.49 |
| Actual load torque (N·m) | 10,034.42 | 16,018.54 | 21,215.22 | 25,188.42 | 29,829.72 | 32,680.25 |
| Relative error | 1.36% | 0.90% | 1.72% | 1.96% | 0.72% | 1.35% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Lv, H.; Zhou, X.; Chen, Z.; Yang, Y. Design and Modeling of a Test Bench for Dual-Motor Electric Drive Tracked Vehicles Based on a Dynamic Load Emulation Method. Sensors 2018, 18, 1993. https://doi.org/10.3390/s18071993
Wang Z, Lv H, Zhou X, Chen Z, Yang Y. Design and Modeling of a Test Bench for Dual-Motor Electric Drive Tracked Vehicles Based on a Dynamic Load Emulation Method. Sensors. 2018; 18(7):1993. https://doi.org/10.3390/s18071993
Chicago/Turabian StyleWang, Zhe, Haoliang Lv, Xiaojun Zhou, Zhaomeng Chen, and Yong Yang. 2018. "Design and Modeling of a Test Bench for Dual-Motor Electric Drive Tracked Vehicles Based on a Dynamic Load Emulation Method" Sensors 18, no. 7: 1993. https://doi.org/10.3390/s18071993
APA StyleWang, Z., Lv, H., Zhou, X., Chen, Z., & Yang, Y. (2018). Design and Modeling of a Test Bench for Dual-Motor Electric Drive Tracked Vehicles Based on a Dynamic Load Emulation Method. Sensors, 18(7), 1993. https://doi.org/10.3390/s18071993





