Analysis of Frequency Stability and Thermoelastic Effects for Slotted Tuning Fork MEMS Resonators
Abstract
1. Introduction
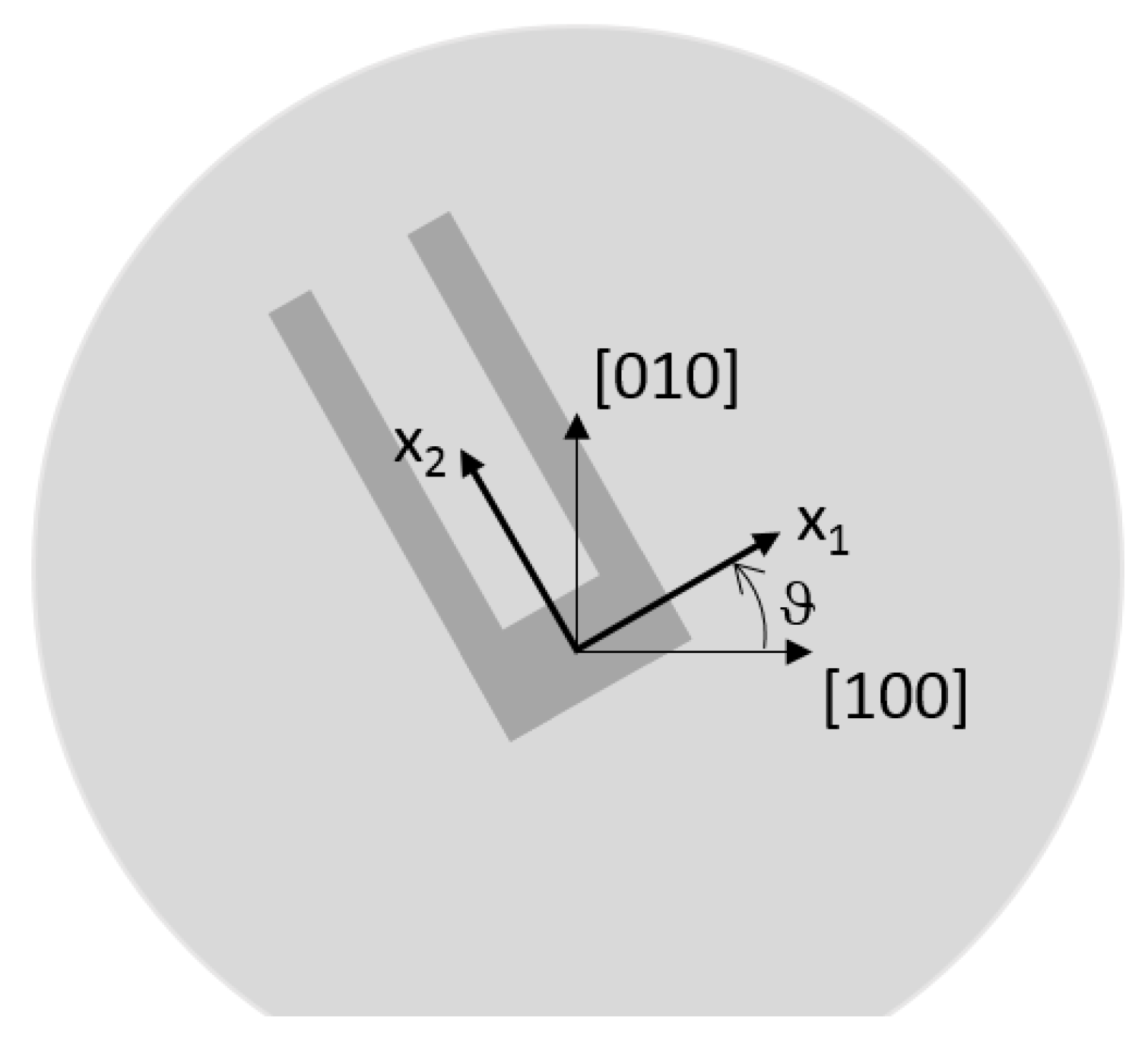
2. Mechanical and Thermal Properties of Single-Crystal Silicon
3. Analytical Model
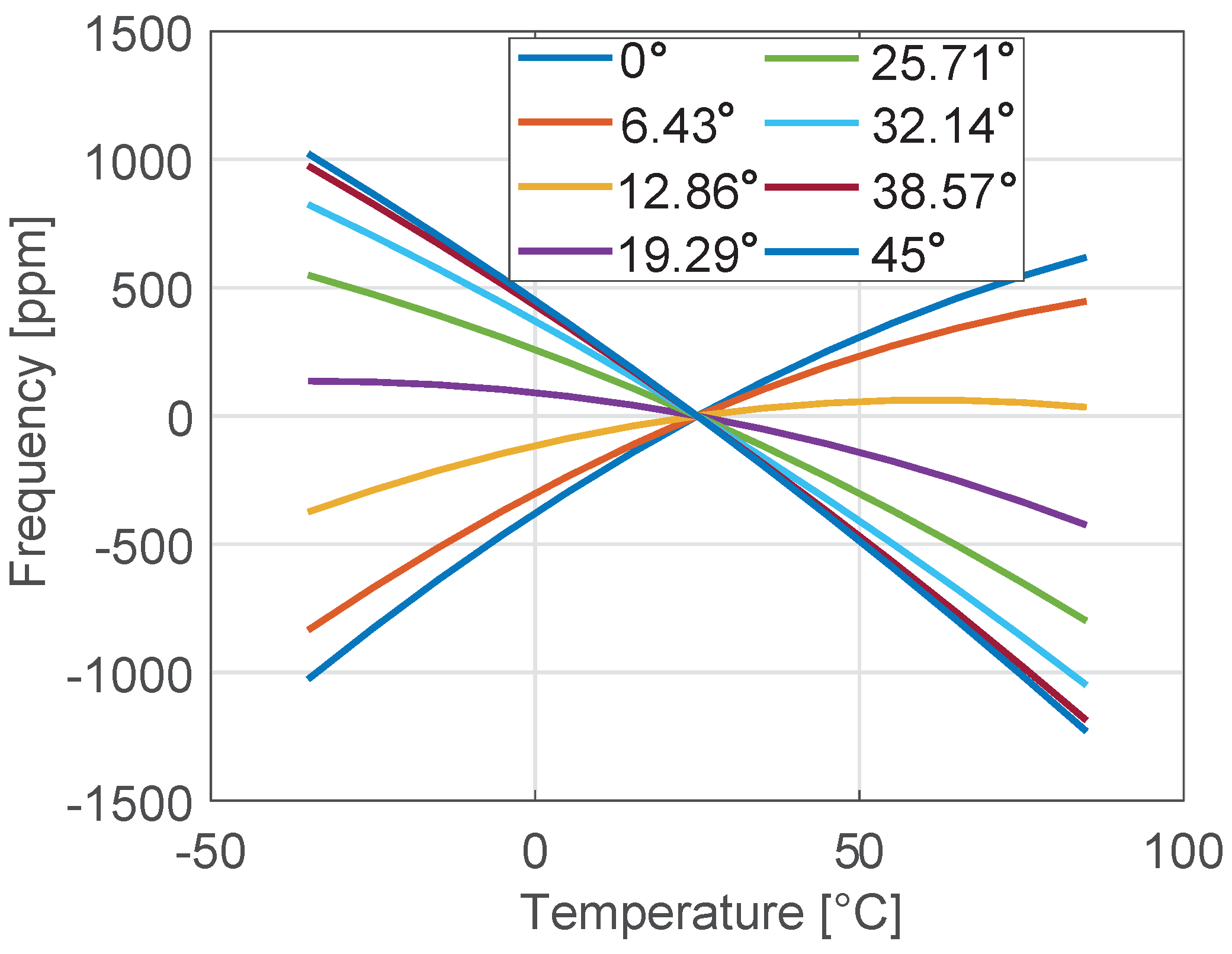
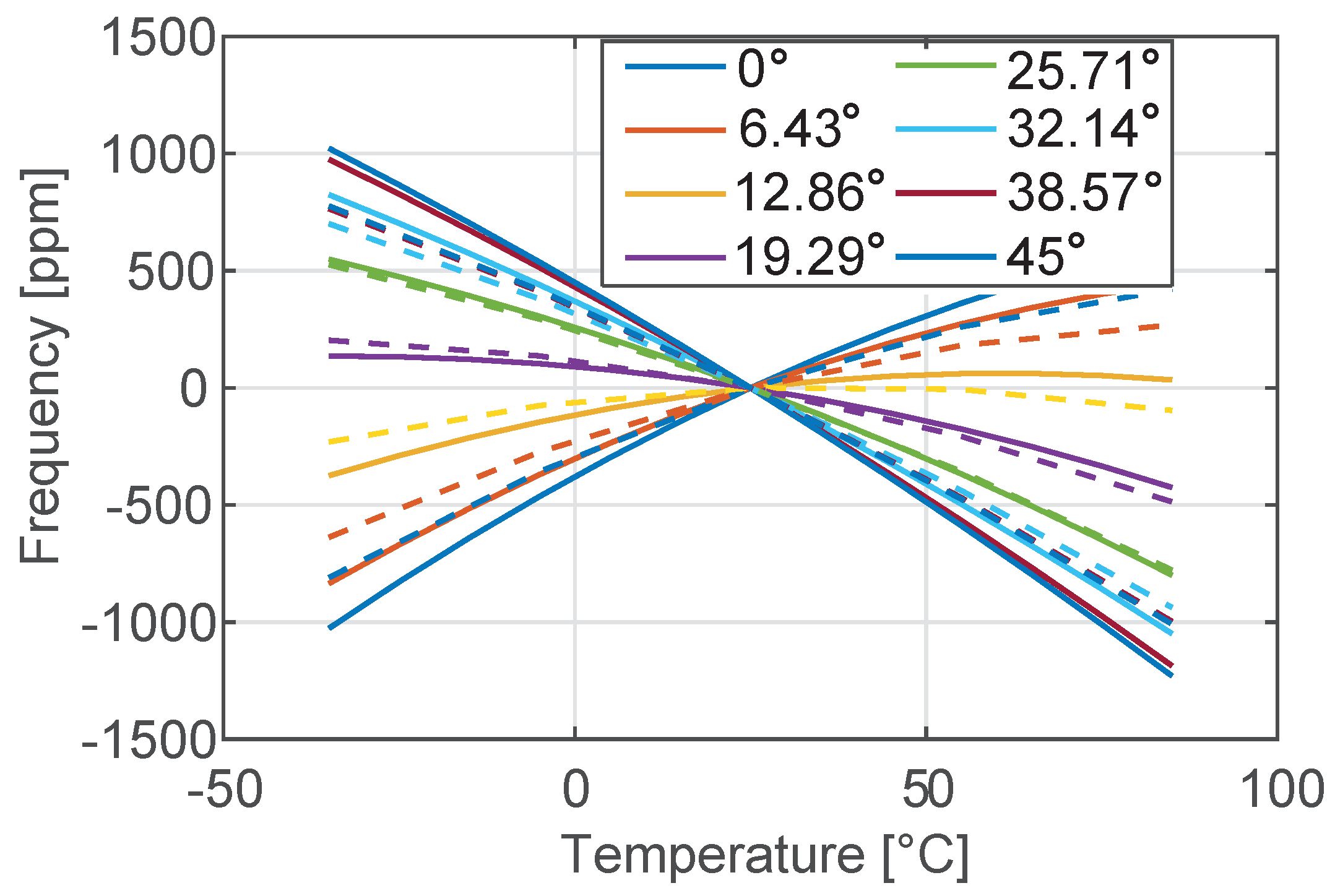
3.1. Temperature Variation of Frequency
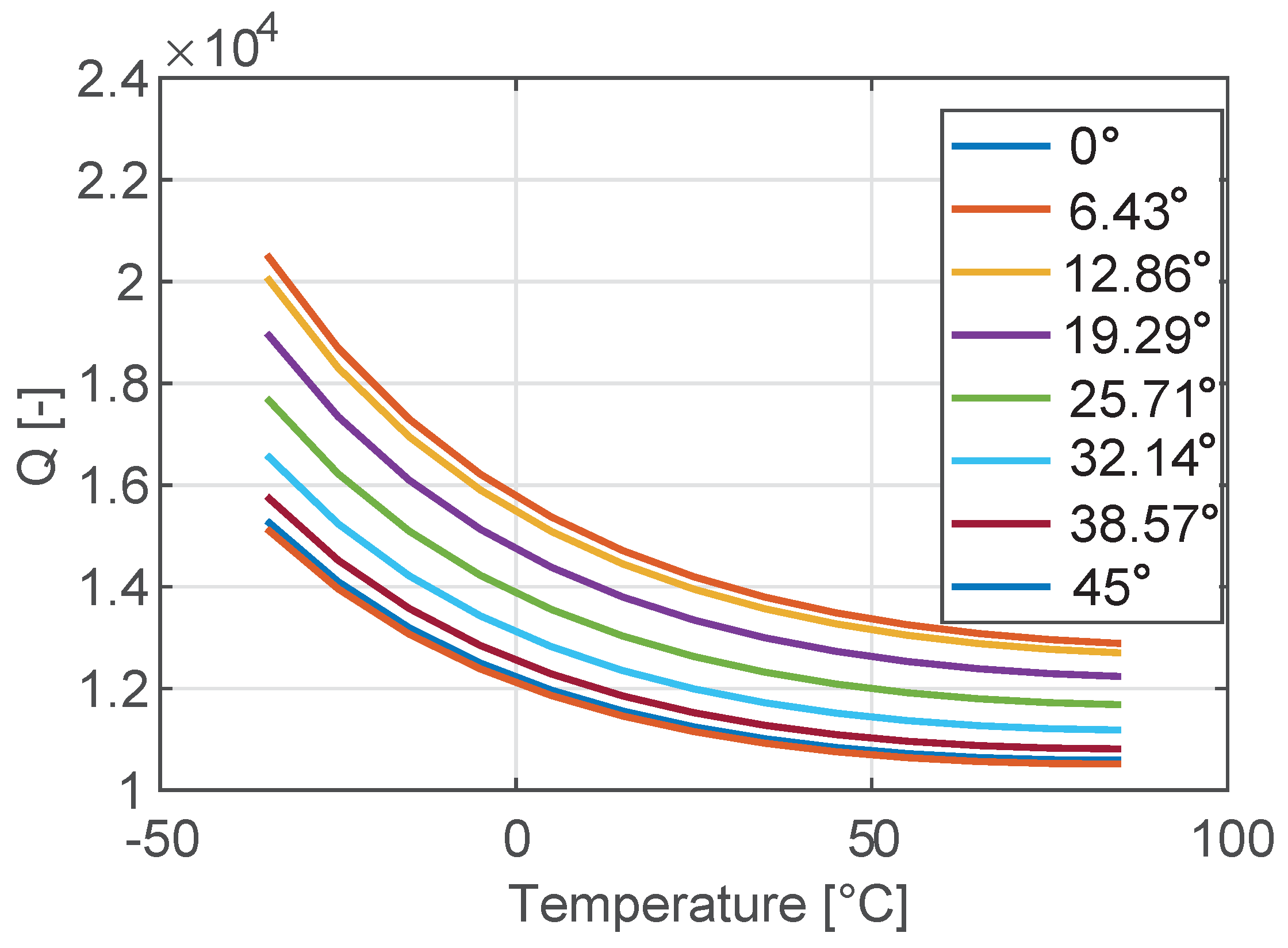
3.2. Temperature Coefficient of Quality Factor
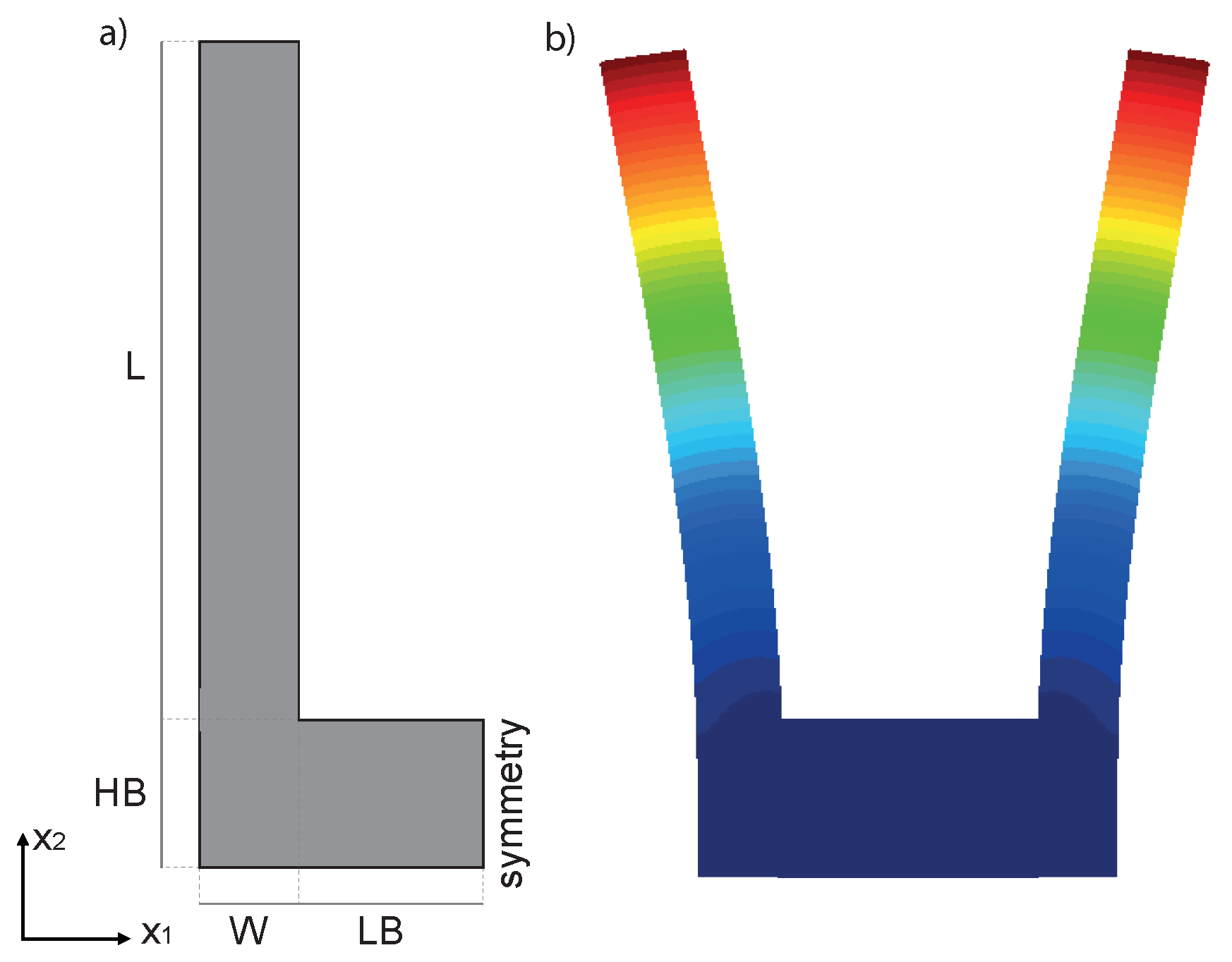
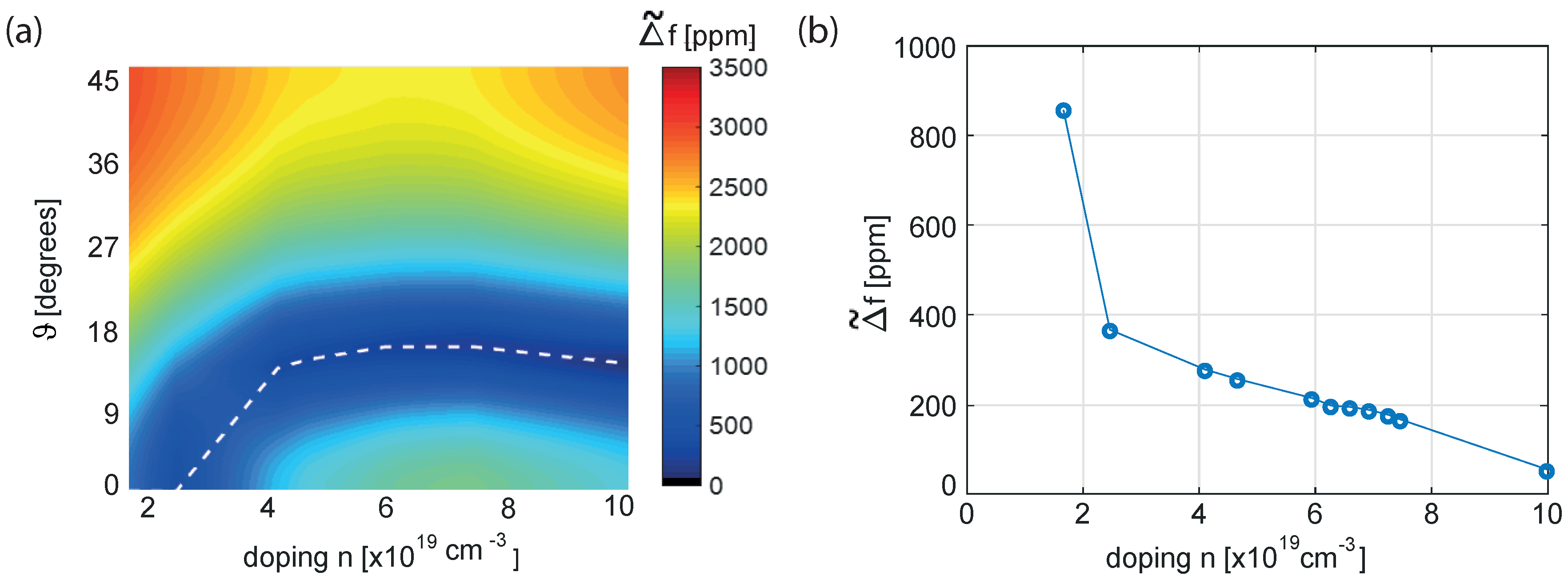
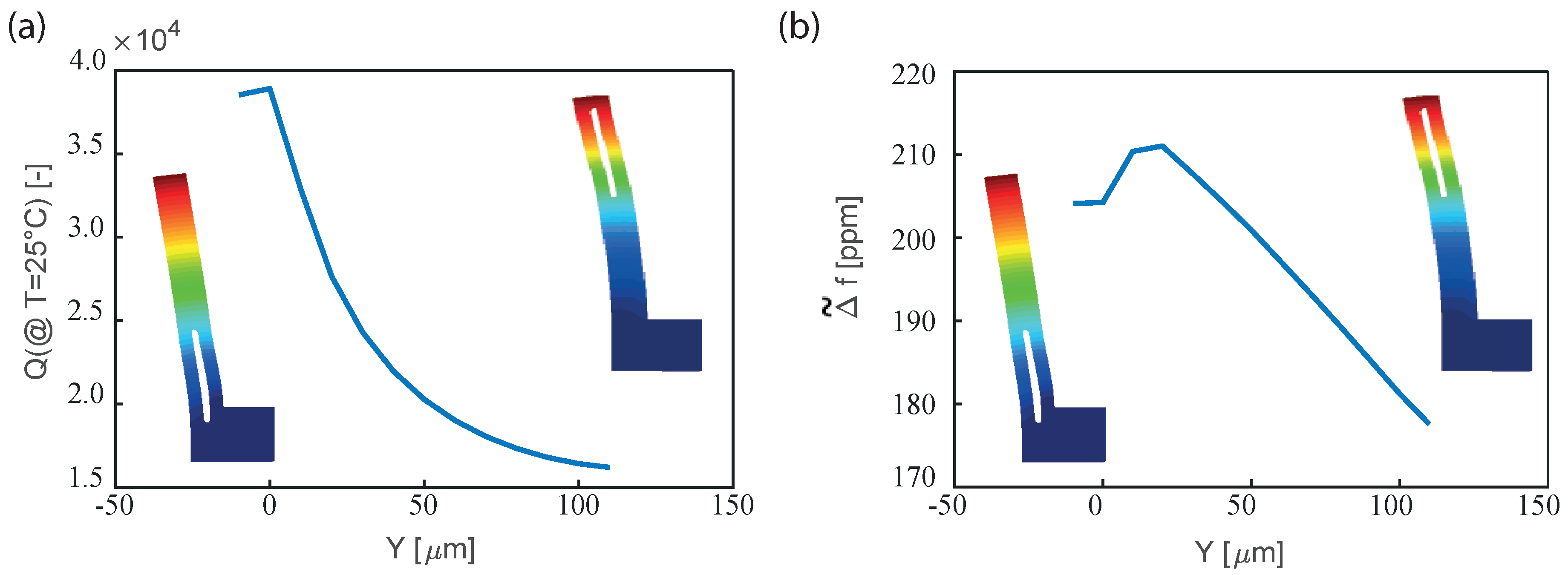
4. Validation on the Real 3D Structure
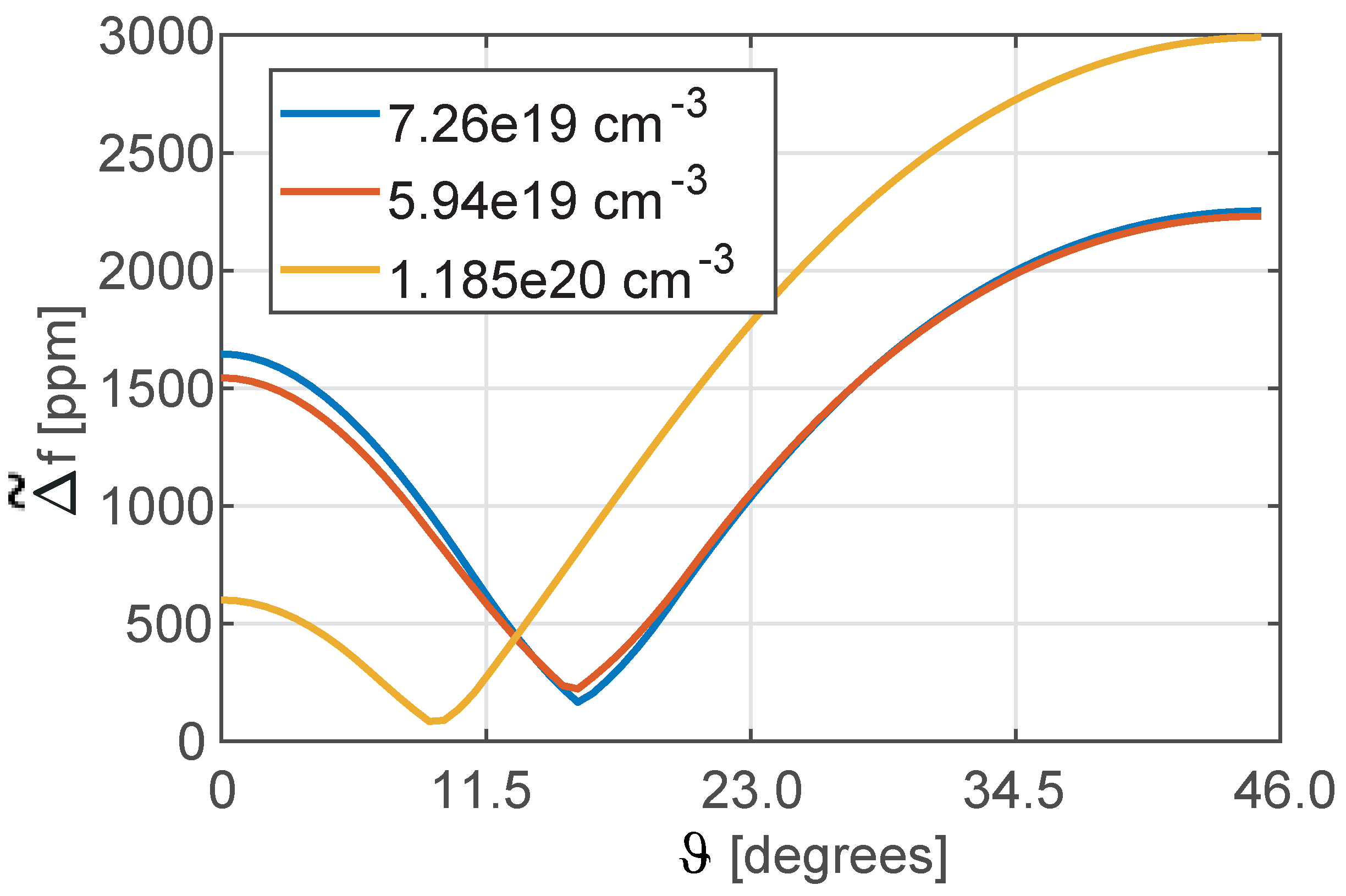
- For a given level of doping and resonant mode type (e.g. bending-mode) the material orientation has a strong impact on and a clear minimum can be achieved. This value is essentially independent of the mode-order and geometric dimensions. The same minima are obtained analytically and numerically, although they might correspond to slightly different rotations of the material axes.
- The impact of material orientation on the Q value is minimal, and the rather low Q is an intrinsic limitation.
5. Optimization of the Tuning Fork Resonator
5.1. Covariance Matrix Adaptation Evolution Strategy Optimization
5.1.1. Q Maximization
5.1.2. Multi-Objective Function
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lam, C.S. A review of the recent development of MEMS and crystal oscillators and their impacts on the frequency control products industry. In Proceedings of the IEEE Ultrasonics Symposium, Beijing, China, 2–5 November 2008; pp. 694–704. [Google Scholar]
- SiTime. SiT1532 Ultra-Small 32 kHz Oscillator. Available online: www.sitime.com (accessed on 9 June 2018).
- Jaakkola, A.; Prunnila, M.; Pensala, T.; Dekker, J.; Pekko, P. Design rules for temperature compensated degenerately n-type doped silicon MEMS resonators. J. Microelectromech. Syst. 2015, 24, 1832–1839. [Google Scholar] [CrossRef]
- Mussi, G.; Bestetti, M.; Zega, V.; Frangi, A.; Gattere, G.; Langfelder, G. Resonators for real-time clocks based on epitaxial polysilicon process: A feasibility study on system-level compensation of temperature drifts. In Proceedings of the IEEE Micro Electro Mechanical Systems (MEMS), Belfast, UK, 21–25 January 2018. [Google Scholar]
- Ng, E.J.; Wang, S.; Buchman, D.; Chiang, C.-F.; Kenny, T.W.; Muenzel, H.; Fuertsch, M.; Marek, J.; Gomez, U.M.; Yama, G.; et al. Ultra-stable epitaxial polysilicon resonators. In Proceedings of the Solid-State Sensors, Actuators and Microsystems Workshop, Hilton Head Island, SC, USA, 3–7 June 2012. [Google Scholar]
- Hsu, W. Resonator miniaturization for oscillators. In Proceedings of the IEEE International Frequency Control Symposium, Honolulu, HI, USA, 19–21 May 2008; pp. 392–395. [Google Scholar]
- Varshni, Y.P. Temperature dependence of the elastic constants. Phys. Rev. B 1970, 2, 3952–3958. [Google Scholar] [CrossRef]
- Jaakkola, A.; Prunnila, M.; Pensala, T.; Dekker, J.; Pekko, P. Determination of doping and temperature dependent elastic constants of degenerately doped silicon from MEMS resonators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 1063–1074. [Google Scholar] [CrossRef] [PubMed]
- Ng, E.J.; Hong, V.A.; Yang, Y.; Ahn, C.H.; Everhart, C.L.M.; Kenny, T.W. Temperature Dependence of the Elastic Constants of Doped Silicon. J. Microelectromech. Syst. 2015, 24, 730–741. [Google Scholar] [CrossRef]
- Mirzazadeh, R.; Saeed Eftekhar, A.; Mariani, S. Micromechanical characterization of polysilicon films through on-chip tests. Sensors 2016, 16, 1191. [Google Scholar] [CrossRef] [PubMed]
- Shin, D.D.; Heinz, D.B.; Kwon, H.-K.; Chen, Y.; Kenny, W. Lateral diffusion doping of silicon for temperature compensation of MEMS resonators. In Proceedings of the IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Lake Como, Italy, 26–29 March 2018. [Google Scholar]
- Chen, Y.; Shin, D.D.; Flader, I.B.; Kenny, T.W. Tri-mode operation of higly doped silicon resonators for temperature compensated timing references. In Proceedings of the IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 January 2017. [Google Scholar]
- Defoort, M.; Taheri-Tehrani, P.; Horsley, D.A. Exploiting nonlinear amplitude-frequency dependence for temperature compensation in silicon micromechanical resonators. Appl. Phys. Lett. 2016, 109, 153502. [Google Scholar] [CrossRef]
- Hsu, W.-T.; Clark, J.R.; Nguyen, T.-C. Mechanically temperature compensated flexural-mode micromechanical resonators. In Proceedings of the International Electron Devices Meeting, San Francisco, CA, USA, 11–13 December 2000. [Google Scholar]
- Luschi, L.; Iannaccone, G.; Pieri, F. Temperature compensation of silicon Lamé resonators using etch holes: theory and design methodology. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2017, 64, 879–887. [Google Scholar] [CrossRef] [PubMed]
- Zadeh, S.A.G.; Saha, T.; Allidina, K.; Nabki, K.; El-Gamal, M.N. Electronic temperature compensation of clamped-clamped beam MEMS resonators. In Proceedings of the 53rd IEEE International Midwest Symposium on Circuits and Systems, Seattle, WA, USA, 1–4 August 2010. [Google Scholar]
- Frangi, A.; Cremonesi, M. Semi-analytical and numerical estimates of anchor losses in bistable MEMS. Int. J. Solids Struct. 2016, 92–93, 141–148. [Google Scholar] [CrossRef]
- Fedeli, P.; Frangi, A.; Laghi, G.; Langfelder, G.; Gattere, G. Near vacuum gas damping in MEMS: Simplified modeling. J. Microelectromech. Syst. 2017, 26, 632–642. [Google Scholar] [CrossRef]
- Frangi, A.; Fedeli, P.; Laghi, G.; Langfelder, G.; Gattere, G. Near vacuum gas damping in MEMS: numerical modeling and experimental validation. J. Microelectromech. Syst. 2016, 25, 890–899. [Google Scholar] [CrossRef]
- Prabhakar, S.; Vengallatore, S. Thermoelastic Damping in Hollow and Slotted Microresonators. J. Microelectromech. Syst. 2009, 18, 725–735. [Google Scholar] [CrossRef]
- Asadi, S.; Sheikholeslami, T.F. Effects of slots on thermoelastic quality factor of a vertical beam MEMS resonator. J. Microsyst. Technol. 2016, 22, 2723–2730. [Google Scholar] [CrossRef]
- Candler, R.N.; Duwel, A.; Varghese, M.; Chandorkar, S.A.; Hopcroft, M.A.; Park, W.-T.; Kim, B.; Yama, G.; Partridge, A.; Lutz, M.; et al. Impact of geometry on thermoelastic dissipation in micromechanical resonant beams. J. Microsyst. Technol. 2006, 15, 927–934. [Google Scholar] [CrossRef]
- Abdolvand, R.; Johari, H.; Ho, G.K.; Erbil, A.; Ayazi, F. Quality factor in trench-refilled polysilicon beam resonators. J. Microsyst. Technol. 2006, 15, 471–478. [Google Scholar] [CrossRef]
- Hopcroft, M.A.; Nix, W.D.; Kenny, T.W. What is the Young’s modulus of silicon? J. Microelectromech. Syst. 2010, 19, 229–238. [Google Scholar] [CrossRef]
- Jaakkola, A. Piezoelectrically Transduced Temperature Compensated Silicon Resonators for Timing and Frequency Reference Applications. Ph.D. Thesis, Aalto University, Helsinki, Finnland, 2016. [Google Scholar]
- Hall, J.J. Electronic effects in the elastic constants of n-type silicon. Phys. Rev. 1967, 161, 756–761. [Google Scholar] [CrossRef]
- Okada, Y. Precise determination of lattice parameter and thermal expansion coefficient of silicon between 300 and 1500 K. J. Appl. Phys. 1984, 56, 314. [Google Scholar] [CrossRef]
- Maycock, P.D. Thermal conductivity of silicon, germanium, III-V compounds and III-V alloys. Solid-State Electron. 1967, 10, 161–168. [Google Scholar] [CrossRef]
- Kim, B.; Hopcroft, M.A.; Candler, R.N.; Jha, C.M.; Agarwal, M.; Melamud, R.; Chandorkar, S.A.; Yama, G.; Kenny, T.W. Temperature dependence of quality factor in MEMS resonators. J. Microelectromech. Syst. 2008, 17, 755–766. [Google Scholar] [CrossRef]
- Corigliano, A.; Ardito, R.; Comi, C.; Frangi, A.; Ghisi, A.; Mariani, S. Mechanics of Microsystems; Wiley: Hoboken, NJ, USA, 2018; ISBN 978-1-119-05383-5. [Google Scholar]
- Hansen, N.; Müller, S.D.; Koumoutsakos, P. Reducing the Time Complexity of the Derandomized Evolution Strategy with Covariance Matrix Adaptation (CMA-ES). Evol. Comput. 2003, 11, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Hansen, N.; Ostermeier, A. Completely Derandomized Self-Adaptation in Evolution Strategies. Evol. Comput. 2001, 9, 159–195. [Google Scholar] [CrossRef] [PubMed]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
- McCall, J. Genetic algorithms for modelling and optimisation. J. Comput. Appl. Math. 2005, 184, 205–222. [Google Scholar] [CrossRef]
- Auger, A.; Hansen, N. Performance Evaluation of an Advanced Local Search Evolutionary Algorithm. In Proceedings of the IEEE Congress on Evolutionary Computation, Scotland, UK, 2–5 September 2005; pp. 1777–1784. [Google Scholar]
- Hansen, N.; Niederberger, S.P.N.; Guzzella, L.; Koumoutsakos, P. A method for handling uncertainty in evolutionary optimization with an application to feedback control of combustion. IEEE Trans. Evol. Comput. 2009, 13, 180–197. [Google Scholar] [CrossRef]
- Fukagata, K.; Kern, S.; Chatelain, P.; Koumoutsakos, P.; Kasagi, N. Evolutionary optimization of an anisotropic compliant surface for turbulent friction drag reduction. J. Turbul. 2008, 9, 1–17. [Google Scholar] [CrossRef]
- Gagne, C.; Beaulieu, J.; Parizeau, M.; Thibault, S. Human-competitive lens system design with evolution strategies. Appl. Soft Comput. 2008, 8, 1439–1452. [Google Scholar] [CrossRef]
- Capellari, G.; Chatzi, E.; Mariani, S. Structural health monitoring sensor network optimization through Bayesian experimental design. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2018, 4, 04018016. [Google Scholar] [CrossRef]
- UQLAB. Available online: www.uqlab.com (accessed on 9 June 2018).
- CMA-ES. Available online: http://cma.gforge.inria.fr/cmaes_sourcecode_page.html (accessed on 26 June 2018).

| Doping Type | Concentration [cm−3] | c11 | c12 | c44 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| dop-n | 3.00 × 1013 [26] | 165.64 | 63.94 | 79.51 | −63.4 | −78.7 | −55.4 | −35 | −56 | −7 |
| dop-n | 1.98 × 1019 [26] | 163.94 | 64.77 | 79.19 | −39.2 | −116.2 | −58.7 | −118 | NaN | −28 |
| P | 4.10 × 1019 [8] | 163 | 65.4 | 79.2 | −34.5 | −133.7 | −67.8 | −115 | 22 | −51 |
| P | 4.66 × 1019 [8] | 162.5 | 65.7 | 79.1 | −32.5 | −131.8 | −68.7 | −110 | 18 | −43 |
| P | 6.60 × 1019 [9] | 164 | 66.7 | 78.2 | −34.2 | −135.17 | −67.8 | −103.04 | −1.1 | −40.26 |
| P | 7.47 × 1019 [8] | 161.4 | 66.1 | 78.5 | −30.7 | −134.9 | −71.9 | −78 | −12 | −31 |
| As | 1.20 × 1019 [9] | 164.2 | 65.6 | 78.6 | −46.58 | −124.61 | −63.12 | −105.41 | 31.73 | −45.21 |
| As | 1.66 × 1019 [8] | 164 | 64.3 | 79.5 | −48.5 | −114.7 | −63.7 | −111 | 25 | −58 |
| As | 2.46 × 1019 [8] | 163.8 | 64.9 | 79.4 | −44.2 | −124.6 | −65.1 | −111 | 34 | −55 |
| Sb | 1.30 × 1018 [9] | 165.6 | 64.4 | 79.3 | −65.5 | −85.08 | −60.92 | −67.85 | −28.1 | −52.81 |
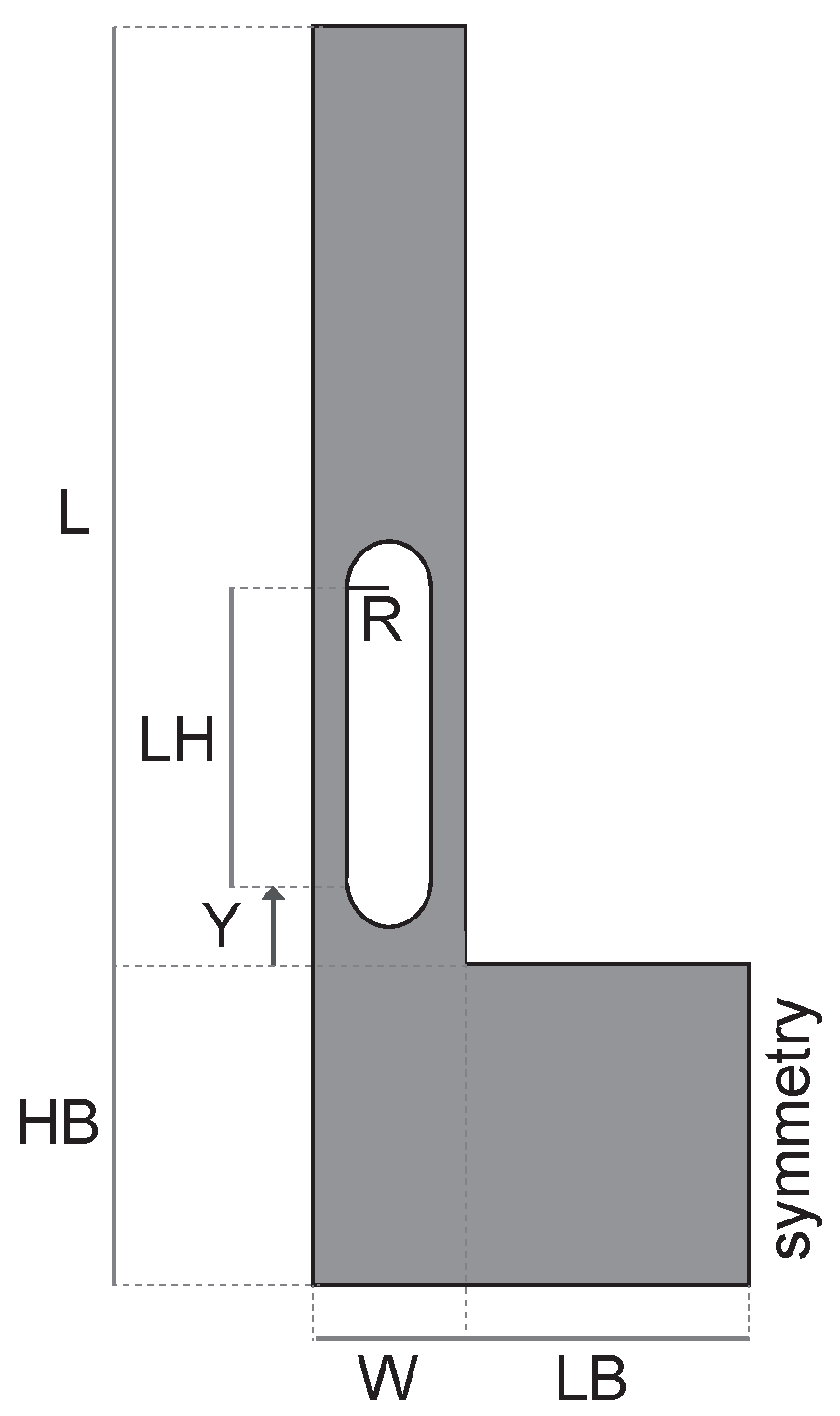
| L | 195 µm |
| HB | 45 µm |
| W | 20 µm |
| LB | 34 µm |
| t | 20 µm |
| Geometry | Optimization Options | Results |
|---|---|---|
 | = [110 3 73 195 20 34 0 45] 0.3 MHz < < 0.7 MHz R < W/2–2.5 µm Y −R > −HB + 2.5 µm Y + LH + R < L −2.5 µm | x = [81.86 14.94 92.05 191.36 34.88 69.95 2.034 68.71] fobj = −Q(@25 °C) = −237831.19 = 0.30 MHz = 1115.21 ppm |
 | = [110 3 73 195 20 34 0 45] 0.4 MHz < < 0.6 MHz R < W/2–4 µm Y − R > −HB + 4 µm Y + LH + R < L −4 µm | x = [−7.27 10.37 64.18 155.44 28.75 66.82 0.09 69.11] fobj = −Q(@25 °C) = −82910.63 = 0.40 MHz = 936.86 ppm |
| Geometry | Optimization Options | Results |
|---|---|---|
 | = [110 3 73 195 20 34 0 45] 0.3 MHz < < 0.7 MHz R < W/2–4.5 µm Y −R > −HB + 4 µm Y + LH + R < L −4 µm | x = [73.69 11.23 122.39 229.05 32.44 37.35 13.32 51.97] Q(@25 °C) = 62534.74 = 0.31 MHz = 171.18 ppm |
 | = [10 3 73 195 20 34 0 45] 0.3 MHz < < 0.7 MHz R < W/2–2.5 µm Y − R>−HB + 2.5 µm Y + LH + R < L −2.5 µm | x = [47.19 7.11 83.50 241.25 31.07 11.95 −12.996 93.35] Q(@25 °C) = 28164.73 = 0.45 MHz = 160.38 ppm |
 | = [110 3 73 195 20 34 0 45] 0.4 MHz < < 0.6 MHz R < W/2–4.5 µm Y −R > −HB + 4 µm Y + LH + R < L −4 µm | x = [90.10 9.68 87.17 239.46 33.20 74.95 −12.834 60.95] Q(@25 °C) = 30955.97 = 0.44 MHz = 167.4 ppm |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zega, V.; Frangi, A.; Guercilena, A.; Gattere, G. Analysis of Frequency Stability and Thermoelastic Effects for Slotted Tuning Fork MEMS Resonators. Sensors 2018, 18, 2157. https://doi.org/10.3390/s18072157
Zega V, Frangi A, Guercilena A, Gattere G. Analysis of Frequency Stability and Thermoelastic Effects for Slotted Tuning Fork MEMS Resonators. Sensors. 2018; 18(7):2157. https://doi.org/10.3390/s18072157
Chicago/Turabian StyleZega, Valentina, Attilio Frangi, Andrea Guercilena, and Gabriele Gattere. 2018. "Analysis of Frequency Stability and Thermoelastic Effects for Slotted Tuning Fork MEMS Resonators" Sensors 18, no. 7: 2157. https://doi.org/10.3390/s18072157
APA StyleZega, V., Frangi, A., Guercilena, A., & Gattere, G. (2018). Analysis of Frequency Stability and Thermoelastic Effects for Slotted Tuning Fork MEMS Resonators. Sensors, 18(7), 2157. https://doi.org/10.3390/s18072157







